Eksponen Titik Dari Sebuah Kelas Digraph Dwiwarna Dengan Satu Loop

EKSPONEN TITIK DARI SEBUAH KELAS DIGRAPH DWIWARNA DENGAN SATU LOOP

SKRIPSI

SITI SAHARA 090803001

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

SKRIPSI

Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai gelar Sarjana Sains

SITI SAHARA 090803001

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

i

PERSETUJUAN

Judul : EKSPONEN TITIK DARI SEBUAH KELAS DIGRAPH

DWIWARNA DENGAN SATU LOOP

Kategori : SKRIPSI

Nama : SITI SAHARA

Nomor Induk Mahasiswa : 090803001

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM

(FMIPA) UNIVERSITAS SUMATERA UTARA

Medan, Juli 2013

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dra. Mardiningsih, M.Si Prof. Dr. Saib Suwilo, M.Sc

NIP.19630405 198811 2 001 NIP.19640109 198803 1 004

Diketahui oleh :

Departemen Matematika FMIPA USU Ketua,

PERNYATAAN

EKSPONEN TITIK DARI SEBUAH KELAS DIGRAPH DWIWARNA DENGAN SATU LOOP

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa ku-tipan dan ringkasan penting yang masing-masing disebutkan sumbernya.

Medan, Juli 2013

iii

PENGHARGAAN

Tak hingga puji serta syukur bagi Tuhan semesta alam, Allah SWT yang me-limpahkan rahmat dan ridho-Nya sehingga penulis dapat menyelesaikan skripsi yang

berjudul ”EKSPONEN TITIK DARI SEBUAH KELAS DIGRAPH

DWI-WARNA DENGAN SATU LOOP” _{ini dengan baik. Shalawat beriring salam}

kepada Nabi Muhammad SAW beserta keluarga dan para sahabat.

Ucapan terima kasih penulis sampaikan kepada Ibunda Nuriah dan Ayahanda Sanudin, dua hamba ALLAH yang tercinta dan terkasih yang sudah bersedia menjadi malaikat pelindung selama perjalanan hidup penulis, kepada Bapak Prof. Dr. Saib Suwilo, M.Sc selaku dosen pembimbing I dan Ibu Dra. Mardiningsih, M.Si selaku dosen pembimbing II yang telah banyak membantu dan memberi dukungan moril, ilmu pengetahuan, nasihat dan motivasi bagi penulis, kepada Bapak Prof. Dr. Tulus, M.Si selaku dosen penguji I dan Bapak Drs. Suwarno Ariswoyo, M.Si selaku dosen penguji II yang telah banyak menyumbang masukan, saran, dan dukungan yang baik dalam menyelesaikan skripsi ini, kepada Bapak Prof. Dr. Sutarman, M.Sc, selaku Dekan FMIPA USU, Bapak Prof. Dr. Tulus, M.Si, dan Ibu Dra. Mardiningsih, M.Si selaku Ketua dan Sekretaris Departemen Matematika di FMIPA USU Medan serta Seluruh Staf Pengajar Depertemen Matematika FMIPA USU yang dengan ikhlas berbagi ilmu pengetahuan selama masa perkuliahan. Semoga ALLAH SWT memuli-akan dan meninggikan derajat mereka serta dinaungi dengan rahmat dan ridho-Nya.

Tak lupa penulis ucapkan terima kasih kepada Abangda dan Kakanda M.Musa, Robby Yanti Fitri, S.Pd, Nurniati, S.Pd, serta Adinda Nurdin, C.SE tersayang yang selalu memberikan doa, dukungan, dan semangat tiada henti kepada penulis, juga kepada keponakan penulis Riski Nazir, Hanapi, Kaylila, Arbi Irsyad dan Aisyah Tahrera yang menggoreskan warna indah dalam hari-hari penulis. Semoga Allah SWT selalu melimpahi rahmat dan barokah-Nya kepada mereka.

Penulis juga mengucapkan terima kasih kepada Misna, Yelli, Kak Titin, Tilla, Putri, Jundi, Bhakti, Lukas, Pancha, Vella, Zati, Fitri, Ade, Matematika 2009, IM3

dan rekan-rekan lainnya yang sudah berbagi asa, cita dan waktu. Semoga Allah SWT memberi balasan atas jasa-jasa mereka yang telah diberikan kepada penulis.

Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu saran dan kritik yang membangun dari pembaca sekalian sangat diperlukan. Akhir kata penulis mengucapkan terima kasih atas perhatiaanya, semoga tulisan ini berguna bagi yang membutuhkan.

Medan, Juli 2013

Penulis

ABSTRAK

Sebuah digraph dwiwarnaD(2) adalah primitif jika terdapat bilangan bulat tak negatif

g dan hsehingga untuk setiap pasang titikudan v diD(2) terdapat (g, h)-walk dari u

kev. Bilangan bulat positifg+hterkecil dari semua bilangan bulat tak negatifg danh

yang demikian disebut eksponen dari digraph dwiwarna D(2) _{dan dinotasikan dengan} expD(2)(v). Misalkanv adalah sebuah titik di D(2). Eksponen dari suatu titikv pada D(2) adalah bilangan bulat positif terkecilg+h sehingga untuk setiap titiku di D(2)

terdapat (g, h)-walk dari titikv ke titiku, dinotasikan dengan expD(2)(v). Tulisan ini

mendiskusikan eksponen titik dari sebuah kelas digraph dwiwarna primitif S₂(2) atas

n ≥ 3 titik yang terdiri dari sebuah n-cycle v1 → vn → vn−1 → · · · → v2 → v1 dan

sebuah loop merah di titik v1. Diperlihatkan bahwa jika n-cycle pada S₂(2) memuat tepat 1 arc biru dan n−1 arc merah, maka eksponen titik dari digraph dwiwarnaS₂(2)

berada pada interval [n−2 +k,2n−3 +k] untuk semua k = 1,2, ..., n

v

VERTEX EXPONENTS OF A CLASS OF TWO - COLORED DIGRAPHS WITH ONE LOOP

ABSTRACT

A two-colored digraph D(2) is primitive provided there are nonnegative integerg and

hsuch that for each pair of verticesuandv there exsist a (g, h)-walk from vertexuto vertexv. The smallest positive integerg+htaken over all such nonnegative integersg

and his the exponent of a two-colored digraph D(2)_{, denoted by exp(D}(2)_{). Letv be a} vertex ofD(2). The exponent of vertexvis the smallest positive integerg+hsuch that for every vertex u in D(2) there is an (g, h)-walk from v to u, denoted by expD(2)(v).

This paper discuss vertex exponent of primitive two colored-digraph S₂(2) on n ≥ 3 vertices consisting the cycle v1 →vn →vn−1 → · · · →v2 →v1 of lengthn and the red

loop at v1. For such two-colored digraph, if n-cycle in S₂(2) exactly has one blue arc andn−1 red arcs, its vertex exponents lie on [n−2+k,2n−3+k] for allk = 1,2, ..., n.

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv

ABSTRACT v

DAFTAR ISI vi

DAFTAR GAMBAR vii

BAB 1 PENDAHULUAN

1.1 Latar Belakang Penelitian 1

1.2 Masalah Penelitian 3

1.3 Tinjauan Pustaka 3

1.4 Tujuan Penelitian 5

1.5 Manfaat Penelitian 5

BAB 2 DIGRAPH DWIWARNA PRIMITIF

2.1 Definisi 6

2.2 Matriks Adjacency 9

2.3 Primitifitas Dari Digraph Dwiwarna Terhubung Kuat 11

2.4 Matriks Tak Negatif dan Eksponen Digraph Dwiwarna 14

2.5 Eksponen Titik Digraph dan Digraph Dwiwarna 21

2.6 Sistem Persamaan Diophantine 24

2.7 Formula Eksponen Titik Digraph Dwiwarna dengan Dua Cycle 25

BAB 3 METODOLOGI PENELITIAN

3.1 Komputasi Nilai Eksponen Titik 30

3.1 Pembuktian Nilai Eksponen Titik 30

BAB 4 EKSPONEN TITIKS₂(2) 32

BAB 5 KESIMPULAN DAN SARAN

5.1 Kesimpulan 47

5.2 Saran 48

vii

DAFTAR GAMBAR

Gambar Halaman

2.1 Digraph dengan 4 titik dan 7 arc 7

2.2 Digraph dwiwarna dengan 5 titik dan 7 arc 8

2.3 Digraph dengan 4 titik dan 7 arc 10

2.4 Digraph terhubung kuat dan tidak terhubung kuat 12

2.5 Digraph terhubung kuat dan primitif 12

2.6 Digraph dwiwarna terhubung kuat dan tidak terhubung kuat 13

2.7 Digraph dwiwarna terhubung kuat dan primitif 14

2.8 Digraph dengan 3 titik dan 6 arc 16

2.9 Digraph dwiwarna dengan 3 titik dan 4 arc 18

4.1 Digraph dwiwarnaS(2)Tipe I 33

4.2 Digraph dwiwarnaS(2)Tipe II 33

ABSTRAK

Sebuah digraph dwiwarnaD(2) adalah primitif jika terdapat bilangan bulat tak negatif

g dan hsehingga untuk setiap pasang titikudan v diD(2) terdapat (g, h)-walk dari u

kev. Bilangan bulat positifg+hterkecil dari semua bilangan bulat tak negatifg danh

yang demikian disebut eksponen dari digraph dwiwarna D(2) _{dan dinotasikan dengan} expD(2)(v). Misalkanv adalah sebuah titik di D(2). Eksponen dari suatu titikv pada D(2) adalah bilangan bulat positif terkecilg+h sehingga untuk setiap titiku di D(2)

terdapat (g, h)-walk dari titikv ke titiku, dinotasikan dengan expD(2)(v). Tulisan ini

mendiskusikan eksponen titik dari sebuah kelas digraph dwiwarna primitif S₂(2) atas

n ≥ 3 titik yang terdiri dari sebuah n-cycle v1 → vn → vn−1 → · · · → v2 → v1 dan

sebuah loop merah di titik v1. Diperlihatkan bahwa jika n-cycle pada S₂(2) memuat tepat 1 arc biru dan n−1 arc merah, maka eksponen titik dari digraph dwiwarnaS₂(2)

berada pada interval [n−2 +k,2n−3 +k] untuk semua k = 1,2, ..., n

v

VERTEX EXPONENTS OF A CLASS OF TWO - COLORED DIGRAPHS WITH ONE LOOP

ABSTRACT

A two-colored digraph D(2) is primitive provided there are nonnegative integerg and

hsuch that for each pair of verticesuandv there exsist a (g, h)-walk from vertexuto vertexv. The smallest positive integerg+htaken over all such nonnegative integersg

and his the exponent of a two-colored digraph D(2)_{, denoted by exp(D}(2)_{). Letv be a} vertex ofD(2). The exponent of vertexvis the smallest positive integerg+hsuch that for every vertex u in D(2) there is an (g, h)-walk from v to u, denoted by expD(2)(v).

This paper discuss vertex exponent of primitive two colored-digraph S₂(2) on n ≥ 3 vertices consisting the cycle v1 →vn →vn−1 → · · · →v2 →v1 of lengthn and the red

loop at v1. For such two-colored digraph, if n-cycle in S₂(2) exactly has one blue arc andn−1 red arcs, its vertex exponents lie on [n−2+k,2n−3+k] for allk = 1,2, ..., n.

PENDAHULUAN

1.1 Latar Belakang Penelitian

Studi mengenai eksponen dari sebuah digraph menjadi pembahasan yang lebih

seder-hana setelah Wielandt (Schneider, H. 2002) mengemukakan sebuah gagasan mengenai

eksponen dari suatu matrikstak negatif A. Matriks tak negatifAadalah sebuah

ma-triks orde n yang setiap entriaij = 0 atau entri aij >0. MatriksA disebut primitif

jika untuk sembarang bilangan bulat positif k, Ak _{adalah positif, yaitu semua entri}

dari matriksAk_{bernilai positif. Bilangan bulat positif terkecilkyang demikian adalah}

eksponen dari matriksA dan dinotasikan dengan exp(A).

Persoalan mengenai eksponen dari sebuah digraph D biasanya diselesaikan

menggunakan matriks D(A), yakni sebuah matriks tak negatif A yang bersesuaian

dengan digraphD. MatriksD(A) adalah sebuah matriks orde ndengan entriaij akan

bernilai 1 jika terdapat arc dari titik vi ke titikvj pada digraph D, dan entriaij akan

bernilai 0 jika tidak terdapat arc dari titikvike titikvj pada digraphD. Eksponendari

digraph D sama dengan eksponen dari matrik tak negatif A yang bersesuaian

den-gan digraph tersebut. Matriks yang bersesuaian denden-gan digraph D kemudian disebut

dengan matriks adjacency.

Sebuah digraph D disebut primitif jika terdapat bilangan bulat positif k

se-hingga untuk setiap pasang titikudanvdiDterdapat walk dariukevdengan panjang

k, nilai terkecilk yang demikian disebut denganeksponendigraphD, dinotasikan oleh

exp(D) (Brualdi dan Ryser, 1991). Wielandt kemudian menyatakan bahwa eksponen

2

(1958). Holladay dan Varga memperlihatkan jika D digraph primitif atas n titik dan

memuat q loop maka exp(D)≤2n−q−1.

Berdasarkan gagasan yang dikemukakan oleh wielandt mengenai eksponen

di-graph, Brualdi dan Liu (1990) kemudian mendefinisikan konsepeksponen lokaldigraph

primitif sebagai berikut. Misalkan D adalah digraph primitif dan v adalah titik di

D. Eksponen dari sebuah titikv merupakan bilangan bulat positif terkecilt sehingga

terdapat walk dengan panjang t dari titikv ke semua titik yang ada diD. Eksponen

dari suatu titikv dinotasikan dengan expD(v). Misalkanv1, v2, ..., vnadalah titik di D

yang diurutkan sehingga expD(v1) ≤ expD(v2)≤ · · · ≤ expD(vn). Untuk 1 ≤ k ≤ n,

exp_D(vk) adalah generalisasi eksponen titik ke-k dari digraph primitifD.

Pada tahun 1997 Fonarsini dan Valcher mendefinisikan suatu digraph dwiwarna

D(2) _{sebagai digraph yang setiap arcnya diwarnai dengan warna merah atau warna} biru. Sebuah digraph dwiwarna D(2) _{disebut terhubung kuat jika untuk setiap pasang}

titik u dan v di D(2) _{terdapat walk dari u ke v dan walk dari v ke u. Sebuah} di-graph dwiwarna terhubung kuat D(2) _{disebut primitif jika terdapat bilangan bulat}

tak negatif g danh sehingga untuk setiap pasang titikudan v diD(2) _{terdapat suatu} (g, h)-walk dariukev. Bilangan bulat positifg+hterkecil atas semua bilangan bulat

tak negatifg dan hyang demikian disebuteksponendariD(2) _{dan dinotasikan dengan} exp(D(2)_{) (Shader dan Suwilo, 2003).}

Konsep eksponen dari digraph dwiwarna primitifD(2) _{yang dikemukakan oleh}

Shader dan Suwilo (2003) didasari karena digraph dwiwarna D(2) _{atas n titik dapat} dinyatakan dalam bentuk matriks adjacencyR dan matriks adjacency B orde n.

Ma-triks AdjacencyR adalah sebuah matriks yang setiap entririj bernilai 1 jika terdapat

arc merah dari titik vi ke titik vj pada D(2), dan bernilai 0 jika tidak terdapat arc

merah dari titik vi ke titik vj pada D(2). Hal yang demikian berlaku juga terhadap

matriks adjacency B, entri bij bernilai 1 jika terdapat arc biru dari titik vi ke titik

D(2)_{. Sehingga permasalahan mengenai eksponen dari sebuah digraph dwiwarna sama}

saja dengan permasalahan memangkatkan matriks tak negatif (R, B) orden sejumlah

(g, h) kali hingga matriks tersebut menjadi matriks positif. Memangkatkan matriks

(R, B) sejumlah (g, h) kali adalah permasalahan kombinatorial, dimana memilihg dan

h agar (R, B)(g,h) _{positif. Hal tersebut dapat dilakukan dengan operasi (g, h)-matriks}

Hurwitz P roduct RdanB yang dapat didefinisikan secara rekurensif seperti berikut.

(R, B)(g,h)_{=R(R, B)}(g−1,h)_{+B(R, B)}(g,h−1)

bilangan positif terkecil dari g+h yang demikian sehingga entri-entri matriks (R, B)

positif, adalah eksponendari digraph dwiwarna D(2)_.

Gao and Shao (2009) mendefinisikan konsep eksponen lokal dari digraph

dwi-warna primitifD(2) _{sebagai berikut. Untuk sembarang titikv}

k diD(2), k = 1,2, ..., n,

eksponen titikvk, dinotasikan dengan expD(2)(vk), adalah bilangan bulat positif

terke-cil p1 +p2 sehingga untuk setiap titik v di D(2) _{terdapat sebuah (p1, p2)-walk dari v}

k

ke v. Untuk kemudahan, titik v1,v2,...,vn dilabel sehingga expD2(v1) ≤ exp_D2(v2) ≤

· · · ≤expD2(vn). Untuk 1≤k≤n, expD2(vk) adalah generalisasi eksponen titik ke-k

dari digraph dwiwarna D(2)_.

1.2 Masalah Penelitian

Andaikan S₂(2) adalah digraph dwiwarna primitif atas n ≥ 3 titik yang terdiri dari

sebuah cycle dengan panjang n dan sebuah loop di titik v1. Untuk setiap titik vk,

k = 1,2, ..., n diS₂(2), berapakah besaran nilai dari exp_S(2) 2 (vk) ?

1.3 Tinjaun Pustaka

Penelitian tentang eksponen digraph dwiwarna pertama sekali dilakukan oleh Shader

dan Suwilo (2003). Shader dan Suwilo memperlihatkan bahwa eksponen terbesar

4

(3n3_{+ 2n}2_{−2n)/2]. Kemudian pada tahun 2009 Gao dan Shao mendiskusikan}

ekspo-nen titik digraph dwiwarna tipe Wielandt, yakni suatu digraph Hamiltonian atas cycle

v1 →vn→ · · · →v2 →v1 dan arc v1 →vn−1 dengan panjang cyclen dan n−1. Gao

dan Shao memperlihatkan jika digraph dwiwarna Wielandt W(2) _{hanya memuat satu} arc biru di va →va−1,a= 2,3, ..., n−1, maka expW(2)(vk) =n2−2n+k−a+ 1. Jika

W(2) _{memuat dua arc biru di v1 →v}

n−1 danv1 →vn maka expW(2)(vk) =n2−2n+k

atau exp_W(2)(vk) =n2−2n+k+ 1.

Berdasarkan generalisasi eksponen digraph dwiwarna yang dikemukakan oleh

Shader dan Suwilo (2003) serta konsep eksponen lokal digraph dwiwarna yang

dike-mukakan oleh Gao dan Shao (2009), banyak peneliti membicarakan eksponen titik

dari beberapa kelas digraph dwiwarna primitif yang memuat dua cycle. Seperti Suwilo

(2011) yang mendiskusikan eksponen titik digraph dwiwarna primitif ekstremal

min-istrong D(2) _{atas n titik dengan panjang cycle n−1 dan n−2. Jika D}(2) _memuat tepat satu arc biru, maka eksponen titik D(2) _{berada pada [n}2_{−5n+ 8, n}2_{−3n+ 1]}

dan jika D(2) _{memuat tepat dua arc biru, maka eksponen titik D}(2) _{berada pada} [n2_{−4n+ 4, n}2_{−n]. Suwilo dan Syafrianty (2012) mendiskusikan eksponen titik}

di-graph dwiwarna primitifD(2) _{atasn = 2mtitik,m≥5 yang memuat dua cycle dengan} panjangn−1 dann−3 berada pada interval [(n3_−5n2_+4n+4)/4,(n3_−5n2_+10n+4)/4].

Syahmarani dan Suwilo (2012) juga mendiskusikan eksponen titik digraph dwiwarna

Hamiltonian L2

n yang terdiri dari cycle v1 → vn → · · · → v2 →v1 dan arc v1 → vn−2

atas n titik ganjil dengan panjang cycle n−2 dan n. Syahmarani dan Suwilo

mem-perlihatkan jika exp(L(2)n ) = (n3−2n2 + 1)/2 maka eksponen titik digraph tersebut

berada pada interval [(n3_−2n2_{−3n+ 4)/4,(n}3_−2n2_{+ 3n+ 6)/4] dan jika exp(L}(2)

n ) =

2n2_{−6n+ 2, maka eksponen titikL}(2)

n berada pada interval [n2−4n+ 5, n2−2n−1].

Semua hasil yang dikemukan oleh periset diatas adalah digraph dwiwarna

prim-itif dengan panjang cycle lebih besar dari satu. Dengan demikian penelitian ini akan

menentukan generalisasi eksponen titik dari sebuah digraph dwiwarna primitif S₂(2),

lain-nya dengan panjang satu atau dikenal dengan istilah loop.

1.4 Tujuan Penelitian

Penelitian ini bertujuan untuk memperoleh generalisasi eksponen titik dari sebuah

kelas digraph dwiwarna primitifS₂(2) atas n≥3 titik dengan satu loop di titik v1.

1.5 Manfaat Penelitian

Penelitian ini bermanfaat untuk memperkaya literatur dibidang eksponen titik

BAB 2

DIGRAPH DWIWARNA PRIMITIF

Pada bagian ini akan diberikan beberapa konsep dasar seperti teorema dan definisi

sebagai landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan

definisi digraph, digraph dwiwarna, terhubung kuat, primitifitas, eksponen dan

ekspo-nen titik digraph dwiwarna yang dirujuk dari Brualdi dan Ryser (1991).

2.1 Definisi

Pada sub-bab ini akan diberikan beberapa definisi tentang digraph dan digraph

dwi-warna serta notasi-notasi yang akan dipergunakan dalam pembahasan selanjutnya.

2.1.1 Digraph

Secara sederhanagraphadalah kumpulan titik atau lingkaran kecil yang dihubungkan

oleh garis. Jika segmen garis tersebut diberi arah maka hal yang demikian disebut

dengan digraph. Formalnya, digraph adalah objek yang terdiri dari dua himpunan

yaitu :

1. Himpunan berhingga tak kosong V = {v0, v1, ..., vm} yang elemen-elemen dari

himpunan V disebut verteks atau titik dari digraph D.

2. Himpunan E yakni himpunan bagian dari pasangan berurut V XV dengan

se-mua titik tidak harus berbeda dan elemen-elemenya disebut arc dari digraph

D.

Jika diberikan α = (u, v) adalah suatu arc diD, maka titik u disebut sebagai

sebagai u→v yang menghubungkan titiku dan v.

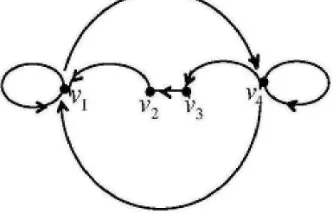
Contoh 2.1.1 Himpunan titik V = {v1, v2, v3, v4} bersamaan dengan himpunan arc E ={v1→v4, v4→v4, v4→v1, v4→v3, v3→v2, v2→v1, v1→v1} adalah suatu digraph

dengan 4 titik dan 7 arc, dinotasikan dengan D(4,7). Representasi grafis digraph

tersebut diperlihatkan seperti pada Gambar 2.1 berikut ini.

Gambar 2.1 Digraph dengan 4 titik dan 7 arc

Andaikan D adalah sebuah digraph. Misalkan u dan v adalah titik di D.

Suatu walk dengan panjang l dari u ke v adalah suatu barisan arc dalam bentuk

u=v0 → v1 → · · · →vl−1 →vl=v

Dengan l > 0,v0 =udan vl =v. Walk tersebut adalah tertutup jikau=v dan walk

disebut terbuka jika u 6= v. Cycle adalah suatu path tertutup uv dan loop adalah

sebuah cycle yang panjangnya satu. Dengan menggunakan digraph pada contoh 2.1.1

akan dijelaskan beberapa definisi diatas.

a. Barisan arcv1→v4→v1→v4→v3→v2→v1 adalah sebuah walk tetapi bukan path

karena ada perulangan titik v1.

b. Barisan arc v1→v4→v3→v2 adalah sebuah path terbuka.

c. Barisan arc v1→v4→v3→v2→v1 adalah sebuah path tertutup dan disebut juga

dengan cycle.

8

2.1.2 Digraph Dwiwarna

AndaikanDadalah sebuah digraph atasntitikv1, v2, ..., vn. Digraph dwiwarnaadalah

sebuah digraph D yang setiap arcnya diwarnai dengan warna merah atau warna biru

dan dinotasikan denganD(2)_{. Sebuah arc merah(u, v) dinotasikan dengan u→}r _{v dan}

sebuah arc biru (u, v) dinotasikan dengan u→b v.

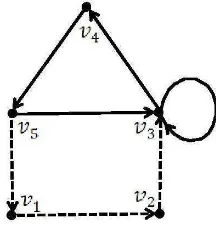
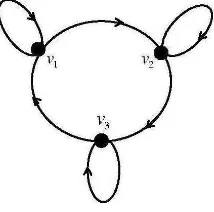
Contoh 2.1.2 Himpunan titik V = {v1, v2, v3, v4, v5} bersama dengan himpunan arc merah R = {(v3, v4) ,(v4, v5) ,(v5, v3),(v3, v3)} dan himpunan arc biru B =

{(v5, v1),(v1, v2),(v2, v3)} adalah sebuah digraph dwiwarna D(2) _{dengan 5 titik, 4 arc} merah dan 3 arc biru. Secara grafis, digraph dwiwarna D(2) _{dapat direpresentasikan}

dengan cara berikut

a. Setiap titik digambarkan dengan lingkaran kecil hitam.

b. Setiap arc merah (a, b) digambarkan dengan garis berarah tidak putus-putus

dari titik a ke titik b.

c. Setiap arc biru (c, d) digambarkan dengan garis berarah putus-putus dari titik

c ke titikd.

Dengan demikian contoh 2.1.2 dapat diperlihatkan pada gambar berikut.

Gambar 2.2 : Digraph dwiwarna 5 titik dan 7 arc

Sebuah (g, h)-walk di digraph dwiwarna D(2) _{adalah walk yang terdiri dari}

g-arc merah dan h-arc biru. Andaikan w adalah sebuah walk. Banyaknya arc merah

dengan panjang walkw adalah l(w) =r(w) +b(w). Vektor 

 r(w)

b(w) 

 disebut sebagai

komposisi dari walk w.

Sebuah pathadalah sebuah walk dengan semua titik-titiknya berbeda. Cycle

adalah path tertutup dan loop adalah cycle dengan komposisi 

 1

0 

 atau 

 0

1 

.

Berdasarakan definisi tersebut, dari Gambar 2.2 diperoleh

a. v1 →b v2 →b v3 →r v3 →r v4 adalah sebuah walk dengan komposisi 

 2

2 

.

b. v1 →b v2 →b v3 →r v4 →r v5 adalah sebuah path terbuka dengan komposisi 

 2

2 

.

c. v5 →r v3 →r v4 →r v5 adalah sebuah cycle dengan komposisi 

 3

0 

.

d. v3 →r v3 adalah sebuah loop dengan komposisi 

 1

0 

.

2.2 Matriks Adjacency

Sebuah digraph D atau digraph dwiwarna D(2) _{atas n titik dapat dinyatakan dalam}

(0,1)-matriks, yaitu sebuah matriks dengan entri 0 atau 1. Matriks yang demikian

dikenal dengan sebutan matriks adjacency.

2.2.1 Matriks Adjacency Digraph

Untuk digraph D atas n titik, matriks adjacency dari D adalah A(D) = [aij]

den-gan ketentuan berikut

aij =

(

1, jika terdapat arc dari vi kevj di D

10

Sebagai contoh perhatikan digraph D pada Gambar 2.3 berikut

Gambar 2.3 : Digraph dengan 4 titik dan 7 arc

matriks adjacency dari digraph pada Gambar 2.3 adalah sebagai berikut

A(D) = 

     

1 1 0 0

0 0 1 0

1 0 1 1

1 0 0 0 

     

2.2.2 Matriks Adjacency Digraph Dwiwarna

Pada digraph dwiwarna D(2)_{, matriks adjacency dariD}(2) _{terbagi atas dua buah} ma-triks adjacency yakni, mama-triks adjacency untuk arc merah, R = [rij] dan matriks

adjacency untuk arc biru, B = [bij] yang masing-masing orde n dengan ketentuan

berikut

rij =

(

1, jika terdapat arc merah darivi kevj diD(2)

0, jika sebaliknya

dan

bij =

(

1, jika terdapat arc biru dari vi kevj di D(2)

0, jika sebaliknya

Dengan demikian, matriks adjacency dari Gambar 2.2 pada contoh 2.1.2 adalah

a. Arc merah dari D(2) _{pada contoh 2.1.2 adalah{v3 →v3, v3 →v4, v4 →v5, v5 →}

v3}. Sehingga matriks adjacency arc merahR= [rij] dari D(2) tersebut adalah

R=          

0 0 0 0 0

0 0 0 0 0

0 0 1 1 0

0 0 0 0 1

0 0 1 0 0          

b. Arc biru dari D(2) _{pada contoh 2.1.2 adalah {v5 → v1, v1 → v2, v2 → v3}.}

Se-hingga matriks adjacency arc biruB = [bij] dari digraph dwiwarnaD(2) tersebut

adalah B =          

0 1 0 0 0

0 0 1 0 0

0 0 0 0 0

0 0 0 0 0

1 0 0 0 0          

2.3 Primitifitas Dari Digraph Dwiwarna Terhubung Kuat

Pada bagian ini akan dibahas tentang digraph dan digraph dwiwarna terhubung kuat

serta primitifitasnya.

2.3.1 Digraph Primitif

Sebuah digraph D disebut terhubung kuat jika untuk setiap pasang titik u dan v

terdapat walk dari titik u kev dan walk dari titikv ke u, sebaliknya digraphD

dise-but tidak terhubung kuat jika terdapat sembarang satu titik atau lebih sehingga tidak

terdapat walk dari u ke v. Berikut ini diberikan contoh digraph terhubung kuat dan

12

Contoh 2.3.1 Representasi dari dua buah digraph terhubung kuat dan tidak ter-hubung kuat.

Gambar 2.4 : Digraph terhubung kuat dan tidak terhubung kuat

Gambar 2.4 menunjukan bahwa (a) adalah terhubung kuat karena terdapat walk dari

satu titik ke titik lainya, sedangkan (b) tidak terhubung kuat karena tidak terdapat

walk dari v1 kev2 .

Misalkan himpunan C = {γ1, γ2, ..., γt} adalah himpunan semua cycle-cycle

yang terdapat pada digrap D dengan panjang dari cycle-cycle tersebut dinotasikan

denganl(γi),i= 1,2, ..., t. Digraph terhubung kuatDdisebutprimitifjika gcd(l(γi)) =

1, sebaliknya digraph D disebuttidak primitifjika gcd(l(γi))6= 1 (Brualdi dan Ryser,

1991). Berikut ini diberikan representasi grafis digraph yang terhubung kuat dan

primitif.

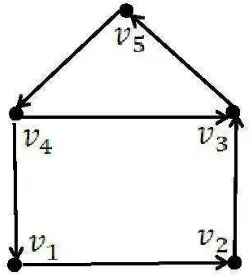
Contoh 2.3.2 Representasi dari digraph terhubung kuat atas 5 titik dan 6 arc.

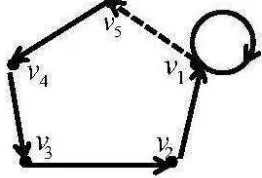
DigraphDpada Gambar 2.5 adalah terhubung kuat yang terdiri dari dua cycle,

yaitu cycleγ1 =v1 →v2 →v3 →v5 →v4→v1 dengan l(γ1) = 5 dan cycleγ2=v4 →

v3 → v5 → v4 dengan panjang l(γ2) = 3. Sehingga gcd(l(γ1), l(γ2)) = gcd(5,3) = 1.

Karena gcd(l(γ1), l(γ2)) = 1, oleh definisi dapat disimpulkan bahwa digraph Dadalah

primitif.

2.3.2 Digraph Dwiwarna Primitif

Sebuah digraph dwiwarnaD(2) _{adalah terhubung kuat jika untuk setiap pasang titiku}

danv diD(2) _{terdapat walk dari titikuke titikv dan walk dari titikv ke titikutanpa} memperhatikan warna setiap arc yang dilalui. Perhatikan contoh digraph dwiwarna

D(2) _{terhubung kuat dan digraph dwiwarna D}(2) _{tidak terhubung kuat berikut}

Contoh 2.3.3 Representasi dari digraph dwiwarna terhubung kuat

Gambar 2.6 : Digraph dwiwarna terhubung kuat dan tidak terhubung kuat

Gambar 2.6 memperlihatkan bahwa (a) adalah digraph dwiwarna D(2)

ter-hubung kuat karena terdapat walk dari satu titik ke titik yang lain dan (b) adalah

digraph dwiwarna D(2) _{yang tidak terhubung kuat karena tidak terdapat walk dariv1}

ke v2.

Sebuah digraph dwiwarna terhubung kuat D(2) _{disebutprimitif jika terdapat} bilangan tak negatif g dan h sehingga untuk setiap pasang titik u dan v di D(2)

terdapat (g, h)-walk dariukev. AndaikanC ={γ1, γ2, ..., γt}adalah himpunan semua

14

orde 2× t dengan setiap kolom ke-i dari M merupakan komposisi dari cycle-cycle

γi, i= 1,2, ..., t seperti berikut

M = "

r(γ1) r(γ2) · · · r(γt)

b(γ1) b(γ2) · · · b(γt)

# .

Sebuah digraph dwiwarna D(2) _{adalah primitif jika dan hanya jika pembagi} perseku-tuan terbesar dari determinan submatriks 2 ×2 dari M adalah ±1 (Fonarsini dan

Valcher, 1997).

Lemma 2.3.1 Andaikan D(2) _{adalah digraph dwiwarna terhubung kuat dengan paling} sedikit satu arc setiap warna. Misalkan M adalah matriks cycle dari D(2)_{. Digraph} D(2) _{adalah primitif jika dan hanya jika content dari matriks M adalah 1.}

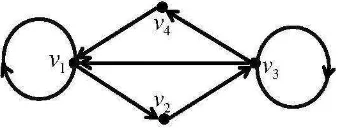
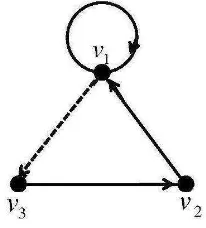
Contoh 2.3.4 Representasi digraph dwiwarna terhubung kuat dan primitif

Gambar 2.7 : Digraph dwiwarna primitif.

Digraph dwiwarna D(2) _{pada Gambar 2.7 adalah terhubung kuat yang terdiri}

dari cycle v1 →b v5 →r v4 →r v3 →r v2 →r v1 dengan komposisi 

 4

1 

 dan loop v1

r → v1

dengan komposisi 

 1

0 

, maka matriks cycle dari D(2) _{adalah M =} 

 1 4

0 1 

dengan

det(M) = 1. Oleh karenadet(M) = 1, maka digraph dwiwarna terhubung kuat D(2) adalah primitif.

2.4 Matriks Tak Negatif dan Eksponen Digraph Dwiwarna

Digraph dwiwarna D(2)_.

2.4.1 Matriks Tak Negatif

Matriks tak negatif A merupakan sebuah matriks yang setiap entri-entri aij dari A

adalah bilangan bulat tak negatif, sebaliknya jika setiap entri-entri aij dari matriks

A adalah bilangan bulat positif maka matriks tersebut disebut matriks positif.

Per-hatikan dua buah matriks berikut ini

N = 

   

5 0 1

3 1 7

0 2 0 

   

, matriks tak negatif; P = 

   

11 2 1

3 1 8

1 4 1 

   

, matriks positif.

2.4.2 Eksponen Digraph

Eksponen dari sebuah digraph D didefinisikan sebagai bilangan bulat positif

terke-cil k sehingga untuk setiap pasang titik u dan v di D terdapat walk dari u ke v

dengan panjang k dan dinotasikan dengan exp(D).

Proposisi 2.4.1 AndaikanAadalah suatu matriks adjacency dari digraphD. Entri ak

ij dari Ak menyatakan banyak walk dari vi ke vj yang panjangnya k di digraph D.

Bukti. Andaikan A adalah suatu matriks adjacency dari digraph D, maka setiap entri (i, j) dariA menyatakan arc dari titikvi kevj di digraph D. Ini mengakibatkan

jika k = 1, maka setiap entri a1

ij dari A1 menyatakan walk dari titik vi ke vj dengan

panjang 1.

Andaikan setiap entri a(ijk) dari Ak menyatakan banyaknya walk dari titik vi

ke vj yang panjangnya k di D, untuk k ≥ 1. Selanjutnya akan diperlihatkan bahwa

16

Perhatikan setiap walk dari titikvi kevj diDdengan panjangk+1 yang terdiri

dari walk vi kevl dengan panjang k untuk l = 1,2, ..., n, dan dilanjutkan dengan arc

dari titikvi kevj, sehinggaa

(k)

il aij menyatakan walk dengan panjangk+ 1 dari titikvi

kevj diDuntukk = 1,2, ..., n. Jika tidak terdapat walk yang panjangnyak dari titik

vi ke vj di D, maka a( k)

il = 0 sehinggaa

(k)

il aij = 0. Hal ini berakibat tidak terdapat

walk yang panjangnya k+ 1 dari titikvi kevj melalui titikvl diDsehingga diperoleh

banyaknya walk yang panjangnya k+ 1 dari titik vi ke vj di D adalah

a_i(₁k)a1j+a_i(₂k)a2j+...+a(_ink)anj = n

X

i=1 ak

ilalj

karena

Ak+1 _=Ak_A

maka

a(ijk)= n

X

i=1 akilalj

Sehingga a(ijk+1) adalah benar menyatakan banyaknya walk dari titik vi ke titik vj

yang panjangnya k+ 1 di D. Berikut ini diberikan contoh dari sebuah digraph yang

akan dicari eksponennya dengan menggunakan proposisi 2.4.1.

Contoh 2.4.1 Representasi digraph dengan 3 titik dan 6 arc.

Gambar 2.8 : Digraph dengan 3 titik dan 6 arc.

Matriks adjacency dari digraph pada Gambar 2.8 adalah sebagai berikut

A= 

  

1 1 0

0 1 1

1 0 1 

Berdasarkan proposisi 2.4.1, banyaknya walk dari titik vi ke titik vj dengan

panjang kdinyatakan oleh entriak

ij dari matriksAk yang semuanya positif. Eksponen

dari digraph D adalah bilangan positif terkecil k yang mengakibatkan matriks Ak

positif. Perhatikan matriks berikut.

a. Untukk = 1; diperoleh A1 ₌ 

  

1 1 0

0 1 1

1 0 1 

  

Bukan eksponen dari digraph pada contoh 2.4.1, karena tidak terdapat walk

dengan panjang 1 dari titik 1 ke titik 3, titik 2 ke titik 1 dan titik 3 ke titik 2.

b. Untukk = 2; diperoleh A2 ₌ 

  

1 2 1

1 1 2

2 1 1 

  

Karena terdapat walk dengan panjang 2 dari tiap pasang titik yang ada di D,

maka eksponen dari digraph pada contoh 2.4.1 adalah exp(D) = 2.

2.4.3 Eksponen Digraph Dwiwarna

Pada digraph dwiwarna D(2)_{, eksponen dari D}(2) _{didefinisikan sebagai bilangan bulat} positif terkecilg+hdari semua bilangan bulat tak negatifg dan hyang ada sehingga

untuk setiap pasang titik u dan v di D(2) _{terdapat sebuah (g, h)-walk dari u ke v} yang terdiri dari g-arc merah dan h-arc biru. Eksponen dari digraph dwiwarna D(2)

dinotasikan oleh exp(D(2)_).

Andaikan A dan B adalah matiks tak negatif orde m. Untuk bilangan tak

negatif g dan h, didefinisikan (g, h)-Hurwitz product, (A, B)(g,h) _{dari A dan B}

adalah jumlah keseluruhan matriks dari hasil perkalian A sebanyak g kali dan B

se-banyakhkali. Sebagai contoh, (A, B)(1,0) _{=A, (A, B)}(0,1)_{=B, (A, B)}(1,1)_=AB+BA

dan (A, B)(2,2)_=A2_B2 _+ABAB+AB2_A+BABA+B2_A2_.

18

maka entri (i, j) dari (R, B)(g,h) _{adalah jumlah (g, h)-walk dari titik uke v diD}(2)_.

Bukti. Lemma 2.4.1 akan dibuktikan dengan induksi pada (g+h) dan (g+h+ 1), jika g = 0 maka h = 1 atau jika g = 1 maka h = 0. Jika g = 0 maka entri (i,j)

dari (R, B)(0,1) _{=B adalah walk dengan komposisi} 

 0

1 

 diD(2). Dengan cara yang

sama, jika h = 0 maka (R, B)(1,0) _{= R adalah walk dengan entri (i, j) menyatakan}

walk dengan komposisi 

 1

0 

 diD(2).

Anggap lemma 2.4.1 benar untuk semua bilangan bulat tak negatif g′

dan h′

dengan g′

+h′

≤g+h, akan diperlihatkan untukg+h+ 1 juga benar dengan catatan

sebagai berikut

(R, B)(g+1,h)_{=R(R, B)}(g,h)_{+B(R, B)}(g+1,h−1)

dengan induksi matematika entri (i, j) pada R(R, B)(g,h) _{adalah walk dari v}

i ke vj

yang dimulai dengan arc merah diikuti oleh sebuah (g, h)-walk dan entri (i, j) pada

B(R, B)(g+1,h−1) _{adalah jumlah walk dari v}

i ke vj yang dimulai dengan sebuah arc

biru dan diikuti oleh sebuah (g+ 1, h−1)-walk sedemikian sehingga entri (i, j) dari

(R, B)(g+1,h) _{adalah jumlah (g+ 1, h)-walk dari i ke j. Perhatikan contoh berikut.}

Contoh 2.4.2 Reprensentasi D(2) _{dengan 3 titik, 3 arc merah dan 1 arc biru}

Matriks adjacency merah dan biru dari Gambar 2.9 adalah R=    

1 0 0

1 0 0

0 1 0 

  

dan B = 

  

0 0 1

0 0 0

0 0 0 

  

Berdasarkan Lemma 2.4.1, banyaknya walk dari titikike titikjdengan panjang

g +h adalah entri (i, j) dari (R, B)(g,h) _{yang semuanya bernilai positif, dan (g+h)}

terkecil dari yang demikian adalah eksponen dari matriks (R, B)(g+h)_{. Perhatikan} matriks (R, B)(g,h) _berikut

a. Untukg+h= 1, maka

1. (R, B)(1,0) _{=R =} 

  

1 0 0

1 0 0

0 1 0 

  

2. (R, B)(0,1) _{=B =} 

  

0 0 1

0 0 0

0 0 0 

  

b. Untukg+h= 2, maka

1. (R, B)(2,0) _=R2 ₌ 

  

1 0 0

1 0 0

1 0 0 

  

2. (R, B)(0,2) _=B2 ₌ 

  

0 0 0

0 0 0

0 0 0 

  

3. (R, B)(1,1) _=RB+BR= 

  

0 1 1

0 0 1

0 0 0 

  

c. Untukg+h= 3, maka

1. (R, B)(3,0) _=R3 ₌ 

  

1 0 0

1 0 0 

20

2. (R, B)(0,3) _=B3 ₌ 

  

0 0 0

0 0 0

0 0 0 

  

3. (R, B)(1,2) _=RB2_{+B(R, B)}(1,1)₌ 

  

0 0 0

0 0 0

0 0 0 

  

4. (R, B)(2,1) _{=R(R, B)}(1,1)_+BR2 ₌ 

  

1 1 1

0 1 1

0 0 1 

  

d. Untukg+h= 4, maka

1. (R, B)(4,0) _=R4 ₌ 

  

1 0 0

1 0 0

1 0 0 

  

2. (R, B)(0,4) _=B4 ₌ 

  

0 0 0

0 0 0

0 0 0 

  

3. (R, B)(1,3) _=RB3_{+B(R, B)}(1,2)₌ 

  

0 0 0

0 0 0

0 0 0 

  

4. (R, B)(2,2) _{=R(R, B)}(1,2)_{+B(R, B)}(2,1)₌ 

  

0 0 1

0 0 0

0 0 0 

  

5. (R, B)(3,1) _{=R(R, B)}(2,1)_+BR3 ₌ 

  

2 1 1

1 1 1

0 1 1 

  

d. Untukg+h= 5, maka

1. (R, B)(5,0) _=R5 ₌ 

  

1 0 0

1 0 0

1 0 0 

2. (R, B)(4,1) _{=R(R, B)}(3,1)_+BR4 ₌ 

  

3 1 1

2 1 1

1 1 1 

  

Karena terdapat walk dengan panjang 5 dari tiap pasang titik pada digraph

dwiwarna D(2)_{, maka eksponen dari digraph dwiwarna D}(2) _{pada Gambar 2.9 adalah}

exp(D2_{) = 5, dengan komposisi} 

 4

1 

 yang terdiri 4 arc merah dan 1 arc biru.

2.5 Eksponen Titik Digraph dan Digraph Dwiwarna

Pada sub-bab ini akan dibahas tentang definisi eksponen titik digraph D dan

ek-sponen titik digraph dwiwarna D(2) _{serta contoh bagaimana menentukan eksponen}

titik dari digraph D dan digraph dwiwarna D(2)_.

2.5.1 Eksponen Titik Digraph

Misalkan D adalah sebuah digraph primitif atas n titik v1, v2, ..., vn. Untuk suatu

vi di D, i = 1,2, ..., n, eksponen titik vi yang dinotasikan dengan expD(vi) adalah

bi-langan bulat positif terkecilt sehingga terdapat walk dengan panjangtdarivikesetiap

titik di D, dan himpunan eksponen exp_D(X) adalah bilangan bulat positif terkecil p

sehingga untuk setiap titikvj diDterdapat sebuah walk dari paling sedikit satu titik

di X ke vj dengan panjang p.

Andaikan D adalah digraph primitif orde n. Jika titik-titik di D adalah

(v1, v2, ..., vn) sedemikian hingga

expD(v1)≤expD(v2)≤ · · · ≤expD(vn)

maka expD(vk) adalah tipe pertama generalisasi eksponen ke-k dari D, dinotasikan

22

Contoh 2.5.1 Berikut ini akan dicari eksponen titik dari tiap masing-masing titik di digraph D pada Gambar 2.9 dengan asumsi bahwa digraph tersebut tidak

diwar-nai dengan merah dan biru. Matriks adjacency dari digraph yang demikian adalah

A= 

  

1 0 1

1 0 0

0 1 0 

  

Berdasarkan Proposisi 2.4.1, eksponen titik dari D diperoleh dengan melihat

entri aij dari Ak, dengan entri pada baris ke-i harus bernilai positif. Perhatikan

matriks Ak _berikut

a. Untuk k = 2, A2 ₌ 

  

1 1 1

1 0 1

1 0 0 

  

. Karena semua entri pada baris pertama dari

matriks A2 _{sudah bernilai positif, maka exp}

D(v1) = 2.

b. Untuk k = 3, A3 ₌ 

  

2 1 1

1 1 1

1 0 1 

  

. Karena semua entri pada baris kedua dari

matriks A3 _{sudah bernilai positif, maka exp}

D(v2) = 3.

c. Untuk k = 4, A4 ₌ 

  

3 1 2

2 1 1

1 1 1 

  

. Karena semua entri pada baris ketiga dari

matriks A4 _{sudah bernilai positif, maka exp}

D(v3) = 4.

Dengan demikian eksponen titik digraph pada Gambar 2.9 tanpa diwarnai

den-gan warna merah dan biru sudah ditemukan yaitu, exp_D(v1) = 2, exp_D(v2) = 3, dan

expD(v3) = 4.

2.5.2 Eksponen Titik Digraph Dwiwarna

MisalkanD(2) _{adalah digraph dwiwarna primitif danV(D}(2)_{) adalah himpunan semua} titik yang ada di D(2) _{dengan V(D}(2)_{) = {v1, v2, ..., vn}. Untuk suatu v}

i ∈ V(D(2))

danX ⊆V(D(2)_{),eksponen titikv}

i yang dinotasikan oleh expD(2)(vi), adalah bilangan

setiap titik di D(2)_{, dan himpunan eksponen exp}

D(2)(X) adalah bilangan bulat positif

terkecilm1+m2 sehingga untuk setiap titikvj diD(2) terdapat sebuah (m1, m2)-walk

dari paling sedikit satu titik di X ke vj.

Andaikan D(2) _{adalah digraph dwiwarna primitif orde n. Jika titik-titik di}

D(2) _{adalah (v1, v2, ..., v}

n) sedemikian hingga

exp_D(2)(v1)≤exp_D(2)(v2)≤ · · · ≤exp_D(2)(vk)

maka expD(2)(v_k) adalah tipe pertama generalisasi eksponen titik ke-k dari digraph

dwiwarna D(2) _{(Gao dan Shao, 2009).}

Untuk mencari eksponen titik digraph dwiwarna primitifD(2)_{, akan dilakukan} dengan operasi (g, h)-matriks Hurwitz Product R dan B yang dapat didefinisikan

se-cara rekurensif. Untuk bilangan bulat tak negatif terkecil g dan h, jika k adalah

adalah titik di D(2)_{, maka semua entri pada baris ke-k dari matriks tersebut bernilai}

positif.

Contoh 2.5.2 Berikut ini akan dicari eksponen titik dari masing-masing titik di di-graph dwiwarnaD(2) _{pada Gambar 2.9, yaitu dengan melihat entri (i, j) dari (R, B)}(g,h)

dimana semua entri pada baris ke-iharus bernilai positif. Menggunakan Contoh 2.4.2

telah diperoleh matriks-matriks (R, B)(g,h)_{, perhatikan bahwa}

a. Untukg+h= 3 pada (R, B)(2,1)_{=R(R, B)}(1,1)_+BR2 ₌ 

  

1 1 1

0 1 1

0 0 1 

   .

Karena semua entri pada baris pertama dari matriks (R, B)(2,1) _{sudah bernilai}

positif, maka exp_D(2)(v1) = 3 dengan komposisi 

 2

1 

 yang terdiri dari 2-arc

merah dan 1-arc biru.

b. Untukg+g = 4 pada (R, B)(3,1)_{=R(R, B)}(2,1)_+BR3 ₌ 

  

2 1 1

1 1 1

0 1 1 

   .

24

positif, maka exp_D(2)(v2) = 4 dengan komposisi 

 3

1 

 yang terdiri dari 3-arc

merah dan 1-arc biru.

c. Untukg+h= 5 dari (R, B)(4,1)_{=R(R, B)}(3,1)_+BR4 ₌ 

  

3 1 1

2 1 1

1 1 1 

   .

Karena semua entri pada baris ketiga dari matriks (R, B)(4,1) _{sudah bernilai}

positif, maka expD(2)(v3) = 5 dengan komposisi 

 4

1 

 yang terdiri dari 4-arc

merah dan 1-arc biru.

Dengan demikian sudah ditemukan eksponen titik dari digraph dwiwarna D(2) _yaitu,

expD(2)(v1) = 3, exp_D(2) (v2) = 4, dan exp_D(2)(v3) = 5.

2.6 Sistem Persamaan Diophantine

Persamaan diophantine adalah suatu persamaan dalam bentuk

a1x1+a2x2+· · ·+anxn=b (1)

dengan solusi dari persamaan tersebut adalah bilangan bulat untuk semua bilangan

bulat a1, a2 ,..., an , b. Andaikan bahwa n ≥ 1 dan koefisien-koefisien a1 , a2 ,..., an

tak semuanya nol.

Teorema 2.6.1Persamaan (1) adalah punya solusi bulat jika dan hanya jika gcd(a1, a2, ..., an)|b.

Sistem persamaan diophantine adalah himpunan dari m persamaan

berikut

a11x1+a12x2+· · ·+a1nxn =b1

a21x1+a22x2+· · ·+a2nxn =b2

...

am1x1+am2x2+· · ·+amnxn =bm

(2)

Sistem persamaan diophantine pada persamaan (2) dapat juga diekspresikan sebagai

sebuah persamaan matriks Ax = b, dimana

A=        

a11 a12 · · · a1n

a21 a22 · · · a2n

..

. ... . .. ...

am1 am2 · · · amn

       

, x =         x1 x2 .. . xn        

, b =         b1 b2 .. . bm         .

Perhatikan bahwa kolom-kolom dari matriksAadalah koefisien-koefisien dari variabel

x1, x2, ..., xn pada persamaan (2). Sistem persamaan diophantine Ax = b adalah

punya solusi bilangan bulat jika dan hanya jika pembagi persekutuan terbesar dari

determinan submatriks 2×2 dari A adalah ±1.

2.7 Formula Eksponen Titik Digraph Dwiwarna dengan Dua Cycle

Di bagian ini akan didiskusikan suatu cara untuk menentukan batas atas dan batas

bawah eksponen titik digraph dwiwarna primitif. Suwilo (2011) menawarkan suatu

teknik untuk menentukan batas atas dan batas bawah eksponen titik digraph

dwi-warna primitif yang memuat dua cycle. Pertama sekali akan diberikan suatu teknik

un-tuk menenun-tukan batas bawah eksponen titik digraph dwiwarna primitif pada Lemma

2.6.1 berikut.

Lemma 2.7.1 Andaikan D(2) _{adalah digraph dwiwarna primitif yang memuat dua}

cycle dengan matrik cycle M = 



r(γ1) b(γ2)

b(γ1) r(γ2) 

26

dari D(2) _{dan terdapat sebuah (g, h)-walk dari titik v}

k ke setiap titik vj di D(2) dengan



 g

h 

 =M   u v  , maka   u v 

 ≥M−1 



r(pk,j)

b(pk,j)



 untuk sembarang bilangan bulat

tak negatif u, v dan untuk suatu path p(k,j) darivk ke vj.

Bukti. Untuk sembarang j = 1,2, ..., n, misalkan pk,j adalah path dari titik vk ke

titik vj. Karena D(2) memuat dua cycle maka setiap walknya dapat didekomposisi

kedalam path dan cycle pada persamaan (3) berikut



 g

h 

=M   x1 x2  +  

r(pk,j)

b(pk,j)



 (3)

dengan x1, x2 ≥ 0. Karena D(2) _{primitif, maka M punya invers. Menggunakan} 

 g

h 

=M 

 u

v 

dan persamaan (3) diperoleh persamaan berikut

M   u v 

=M   x1 x2  +  

r(pk,j)

b(pk,j)

  M   x1 x2 

=M   u v  −  

r(pk,j)

b(pk,j)

    x1 x2  =   u v 

−M−1 



r(pk,j)

b(pk,j)



≥0

sehingga   u v 

≥M−1 



r(pk,j)

b(pk,j)



 dan Lemma (2.7.1) terbukti.

Berdasarkan informasi yang ada pada pembuktian Lemma (2.7.1), diperoleh teorema

berikut ini.

Teorema 2.7.1 Andaikan D(2) _{adalah digraph dwiwarna primitif yang terdiri dari} cycle γ1 dan γ2. Misalkan vk adalah titik di D(2). Untuk sembarang titik vi dan vj di

D(2)_{, definisikan u0 = b(γ2)r(p}

k,j)−r(γ2)b(pk,j) dan v0 = r(γ1)b(pk,j)−b(γ1)r(pk,j).

Maka   g h 

≥M 

 u0

v0 

Bukti. Andaikan bahwa eksponen titik vk dicapai oleh (g, h)-walk dengan   g h   = M   u v 

 dan diperoleh persamaan berikut



 u

v 

≥M−1 



r(pk,j)

b(pk,j)



= 



b(γ2)r(pk,j)−r(γ2)b(pk,j)

r(γ1)b(pk,j)−b(γ1)r(pk,j)



 (4)

untuk sembarang path pk,j dari titik vk ke titik vj.

Jika untuk sembarang titik vj, j = 1,2, ..., n diperoleh nilai b(γ2)r(pk,j) −

r(γ2)b(pk,j)≥0, maka definisikan

u0 =b(γ2)r(pk,j)−r(γ2)b(pk,j)≥0 (5)

dan jika untuk sembarang titikvi,i= 1,2, ..., ndiperoleh nilair(γ1)b(pk,i)−b(γ1)r(pk,i)≥

0, maka definisikan

v0 =r(γ1)b(pk,i)−b(γ1)r(pk,i)≥0 (6)

sehingga u≥u0 dan v ≥v0. Oleh Lemma (2.6.1) diperoleh



 g

h 

=M 

 u

v 

≥M   u0 v0   (7)

sehingga exp_D(2)(vk) =g+h≥(r(γ1) +b(γ1))u0+ (r(γ2) +b(γ2))v0 =l(γ1)u0+l(γ2)v0.

Proposisi 2.7.1 berikut ini diberikan untuk menentukan batas atas eksponen

titik digraph dwiwarna primitif dari sebuah titik yang ditentukan, sebut titik

terse-but v. Definisikan d(vk, v) sebagai jarak dari titik vk ke titik v, yakni panjang walk

terpendek dari vk ke v.

28

1,2, ..., n di D(2)_{, exp}

D(2)(vk)≤expD(2)(v) +d(vk, v).

Bukti. Untuk setiap k = 1,2, ..., n misalkan pk,v adalah (r(pk,v), b(pk,v))-path dari

vk ke titik v dengan panjang d(vk, v). Karena eksponen titik v adalah expD(2)(v),

maka terdapat (g, h)-walk dengan panjang expD(2)(v) = g +h dari v ke setiap titik

vj, j = 1,2, ..., n. Ini menunjukan bahwa setiap titik vk di D(2) terdapat suatu

(g +r(pk,v), h+b(pk,v))-walk dari titik vk ke setiap titik vj. Walk tersebut berawal

dari vkmenujuv melalui (r(pk,v), b(pk,v))-path dan kemudian menujuvj melalui suatu

(g, h)-walk dari v kevj. Oleh karena itu diperoleh expD(2)(vk)≤expD(2)(v) +d(vk, v)

Proposisi 2.7.2 berikut diberikan untuk menentukan batas atas eksponen titik

digraph dwiwarna primitif yang memuat dua cycle.

Proposisi 2.7.2 Andaikan D(2) _{adalah digraph dwiwarna yang terdiri atas cycle γ1} dan γ2. Misalkan vk adalah titik di D(2) yang terdapat pada cycle γ1 dan cycle γ2.

Jika untuk setiapi= 1,2, ..., ndan sembarang bilangan bulat positifg danh, terdapat

path pk,i dari vk kevi sehingga sistem persamaan

Mx + 



r(pk,i)

b(pk,i)



= 

 g

h 

 (8)

punya solusi bilangan bulat tak negatif, maka expD(2)(vk)≤g+h.

Bukti. Misalkan bahwa solusi dari sistem persamaan (8) adalah x = (x1, x2)T. Karena D(2) _{adalah primitif, maka matriks cycle M adalah invertible, sehingga x1} dan x2 tidak dapat nol kedua-duanya. Karena x1, x2 6= 0 dan kedua cycleγ1 dan γ2

memuat titik vk, maka terdapat tiga kemungkinan berikut.

Jika x1 > 0 dan x2 > 0, maka walk dari titik vk ke titik vi akan bergerak

sebanyakx1kali mengelilingi cycleγ1 dan bergerak sebanyakx2kali mengelilingi cycle

γ2 dan kembali lagi ke titik vk, kemudian terus bergerak menuju titikvi di sepanjang

walk dari titik vk ke titik vi akan bergerak sebanyakx2 kali mengelilingi cycle γ2 dan

kembali lagi ke titik vk, kemudian terus bergerak menuju titik vi di sepanjang path

pk,i adalah sebuah (g, h)-walk dari vk kevi. Jika x1 >0 dan x2 = 0, maka walk dari

titik vk ke titik vi akan bergerak sebanyak x1 kali mengelilingi cycle γ1 dan kembali

lagi ke titikvk, kemudian terus bergerak menuju titikvi di sepanjang pathpk,i adalah

sebuah (g, h)-walk dari vk kevi. Dengan demikian, untuk setiap titikvi, i= 1,2, ..., n

BAB 3

METODE PENELITIAN

Untuk menentukan eksponen titik dari sebuah kelas digraph dwiwarna primitif S₂(2) yang memuat sebuah loop di titik v1 dan sebuah cycle dengan panjang n, akan

digu-nakan teknik-teknik yang telah dikembangkan oleh Suwilo (2011). Pendekatan akan

dilakukan dalam langkah berikut:

3.1 Komputasi Nilai Eksponen Titik

Dengan menggunakan program two exp, akan ditemukan bilangan bulat tak negatifg

dan hsehingga

exp_S(2)

2 (vk) =g+h.

Hal ini dilakukan dengan menghitung hasil kali (g, h)-Hurwzit dari matriks

ad-jacency R dan B secara rekursif sehingga (R, B)(g,h) _positif.

3.2 Pembuktian Nilai Eksponen Titik

Dengang danhyang sudah ditemukan pada langkah (3.1), langkah berikutnya adalah

membuktikan bahwa exp_S(2)

2 (vk) =g+h. Untuk itu, hal pertama yang harus dilakukan adalah memperlihatkan bahwa exp_S(2)

2 (vk)≥g+h, yakni dengan menemukan bilangan tak negatif u0 dan v0 sedemikian hingga



 g

h 

≥M 

 u0

v0 



sehingga exp_S(2)

dari cycle γ2.

Langkah selanjutnya adalah memperlihatkan bahwa exp_S(2)

2 (vk)≤g+h. Karena digraph dwiwarna S₂(2) adalah primitif, maka determinan dari matriks cycleM adalah

±1 dan setiap walk pada digraph dwiwarna S₂(2) dapat didekomposisi menjadi suatu

path dari titikvk ke titikvi dan beberapa buah cycle, sehingga untuk memperlihatkan

exp_D(2)(vk)≤g+h, cukup diperlihatkan bahwa sistem persamaan diophantine

M 

 x1

x2 

+ 



r(pk,i)

b(pk,i)



= 

 g

h 

, i= 1,2, ..., n

punya solusi bulat tak negatif yaitu x1, x2 ≥ 0 untuk semua titik vi dan beberapa

path pk,i dari titikvk ke titik vi.

Dengan memperlihatkan exp_D(2)(vk) ≥ g+h dan expD(2)(vk) ≤ g +h, maka

BAB 4

EKSPONEN TITIK S2(2)

Andaikan S₂(2) adalah sebuah digraph dwiwarna primitif atas n ≥ 3 titik yang ter-diri dari sebuah n-cycle v1 → vn → vn−1 → · · · → v2 → v1 dan sebuah loop di

titik v1. Dengan menggunakan sifat primitifitas dari sebuah digraph dwiwarna, akan

ditentukan warna setiap arc pada S₂(2). Andaikan γ1 dan γ2 adalah cycle-cycle yang

terdapat padaS₂(2). Karena loop juga merupakan sebuah cycle, misalkanγ1 adalah cy-cle v1 →v1 dengan panjang 1, dan γ2 adalah cyclev1→vn→vn−1 → · · · →v2 →v1

dengan panjang n. Sehingga matriks cycle dari S₂(2) dapat dinyatakan dalam

ben-tuk M1 = 



1−a n−b

a b



 atau M2 = 



a b

1−a n−b 

, untuk sembarang

bilan-gan bulat 0 ≤ a ≤ 1 dan 0 ≤ b ≤ n. Karena digraph dwiwarna S₂(2) primitif,

maka content dari matriks cycle S₂(2) adalah 1, yaitu det(M1) = b−na = ±1 atau det(M2) = na− b = ±1 dipenuhi jika dan hanya jika a = 0 dan b = 1. Dengan

demikian matriks cycle dari S₂(2) harus M1 = 



1 n−1

0 1



 atauM2 = 



0 1

1 n−1 

.

Tanpa mengurangi keumuman pembuktian, diasumsikan bahwa matriks cycle

dari digraph dwiwarna primitif S₂(2) adalah M = 



1 n−1

0 1



. Dengan demikian,

cycle γ1 dengan panjang 1 adalah sebuah loop merah, dan cycleγ2 dengan panjang n

adalah cycle yang terdiri dari n−1 arc merah dan tepat satu arc biru. Lebih jauh,

digraph dwiwarna primitifS₂(2)diklasifikasikan atas tiga tipe berdasarkan arc biru dan

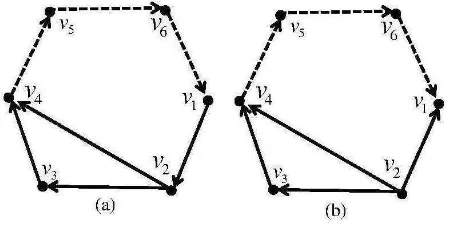
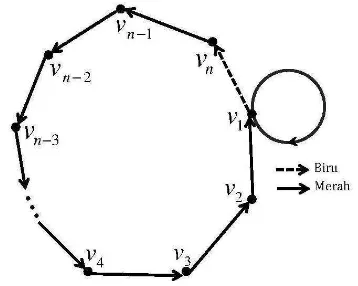
1. Digraph dwiwarnaS2(2)adalah tipe I jika arc biru dariγ2 adalah arcv2 →v1 dan path merah dengan panjangn−1 adalah pathv1 →vn →vn−1 → · · · →v3 →v2

[image:44.612.256.432.154.295.2]

seperti pada gambar berikut

Gambar 4.1 Digraph Dwiwarna S₂(2) Tipe I

2. Digraph dwiwarna primitif S₂(2) adalah tipe II jika arc biru dari γ2 adalah arc v1 →vn dan path merah dengan panjangn−1 adalah pathvn→vn−1 → · · · →

v2 →v1 seperti pada gambar berikut

Gambar 4.2 Digraph Dwiwarna S₂(2) Tipe II

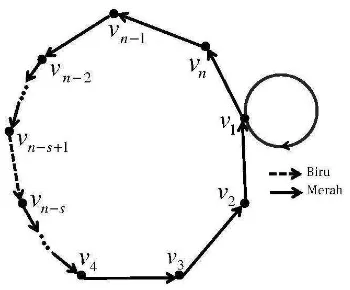
3. Digraph dwiwarna primitifS₂(2) adalah tipe III jika arc biru dari γ2 adalah arc

vn−s+1 →vn−s,s = 1,2, ..., n−2 dan path merah dengan panjang n−1 adalah

[image:44.612.252.431.417.560.2]

[image:45.612.255.430.77.222.2]

34

Gambar 4.3 Digraph Dwiwarna S₂(2) Tipe III

Eksponen titik dari digraph dwiwarna S₂(2) tipe I, II dan III akan diperlihatkan

pada Lemma (4.1), Lemma (4.2) dan Lemma (4.3) berikut.

Misalkan S₂(2) adalah digraph dwiwarna primitif seperti Gambar 4.1, 4.2 dan 4.3 serta ditetapkan vk sebagai titik diS2(2). Lemma (2.7.1) menegaskan bahwa

ekspo-nen titik dari digraph dwiwarna primitif bergantung sekali terhadap seberapa besar

bilangan u0 pada persamaan (5) dan v0 pada persamaan (6). Ingat bahwa bilangan

u0 akan besar saat pk,j memuat arc merah sebanyak mungkin dan memuat arc biru

sesedikit mungkin, dan nilai v0 akan besar saat path pk,j memuat arc biru sebanyak

mungkin dan arc merah sesedikit mungkin.

Lemma 4.1 AndaikanS₂(2)adalah digraph dwiwarna primitif tipe I, makaexp_S(2) 2 (vk) = n−2 +k untuk semua k = 1,2, ..., n.

Bukti. Berikut ini diperlihatkan bahwa eksponen titik dari digraph dwiwarna primi-tif S₂(2)adalah exp_S(2)

2 (vk) = n−2 +k untuk semuak= 1,2, ..., n. Karena path merah dengan panjang n−1 adalah path v1 → vn → vn−1 → · · · → v3 → v2, maka dapat

dipilih x∗ _{= v1 dan y}∗ _{= v2 sebagai titik awal dan titik akhir. Andaikan v}

k adalah

titik di S₂(2). Akan digunakan pathpk,y∗ dariv_k key∗ untuk menentukan nilaiu0 pada

persamaan (5) dan pathpk,x∗ darivkkex∗ untuk menentukan nilaiv0pada persamaan

1. Kasus k = 1

Pertama akan diperlihatkan bahwa batas bawah eksponen titik dari digraph dwiwarna

primitifS₂(2)adalah exp_S(2)

2 (vk)≥n−2+k. Untuk itu pilihy

∗ _{=v2, terdapat tepat satu}

pathpvk,v2 dari titikvkke titikv2, yakni (k+n−2,0)-path denganr(pk,y∗) =k+n−2

dan r(bk,y∗) = 0. Menggunakan path tersebut dan persamaan (5) diperoleh

u0 =b(γ2)r(pk,y∗)−r(γ2)b(pk,y∗) = 1(k+n−2)−(n−1)0 =n−2 +k. (9)

Pilihx∗ _{=v1, path p}

vk,v1 dari titikvk ke titik v1 adalah (1,0)-path dan (k+n−2,

1)-path. Menggunakan (k+n−2,1)-path pvk,v₁ dan persamaan (6) diperoleh

v0 =r(γ1)b(pk,x∗)−b(γ1)r(pk,x∗) = 1(1)−0(k+n−2) = 1. (10)

Menggunakan (1,0)−path dan persamaan (6) diperoleh

v0 =r(γ1)b(pk,x∗)−b(γ1)r(p_k,x∗) = 1(0)−0(1) = 0. (11)

Karena batas bawah tercapai bila nilai v0 kecil, dari persamaan (10) dan (11) pilih

v0 = 0. Menggunakan Lemma (2.7.1), persamaan (9) dan (11) diperoleh



 g

h 

≥M   u0 v0  =  

1 n−1

0 1



 



n−2 +k

0



= 



n−2 +k

0



 (12)

sehingga

exp_S(2)

2 (vk)≥ n−2 +k (13)

untuk k = 1.

Dengan memperhatikan persamaan (12), berikut ini akan diperlihatkan bahwa

untuk k = 1, batas atas eksponen titik dari digraph dwiwarna primitif S₂(2) adalah

exp_S(2)

2 (vk)≤n−2 +k. Untuk itu cukup diperlihatkan bahwa sistem persamaan

M   x1 x2  +  

r(p1,1)

b(p11) 

= 

 n−1

0 

36

punya solusi bulat tak negatif, yaitu x1 ≥0 dan x2 ≥0.

Karena S₂(2) adalah digraph dwiwarna primitif, maka matriks cycle M adalah

invertible dengan M−1 ₌





1 1−n

0 1



, sehingga solusi dari persamaan (14) adalah



 x1

x2 

= 



1 1−n

0 1



 



n−1−r(p1,1) 0−b(p1,1)



= 



n−1−r(p1,1)−b(p1,1)(1−n) −b(p1,1)





Path p1,1 dari titik v1 ke titik v1 dapat dipilih (1,0)-path dengan r(p1,1) = 1

dan b(p1,1) = 0, diperoleh x1 = n − 2 > 0 dan x2 = 0. Karena persamaan (14)

punya solusi bulat tak negatif dan titikv1terletak di cycleγ1 danγ2, Proposisi (2.7.2)

menjamin bahwa

exp_S(2)

2 (vk)≤n−2 +k. (15)

Menggunakan persamaan (13) dan (15) diperoleh

exp_S(2)

2 (vk) =n−2 +k (16)

untuk k = 1.

Untuk kasus 2 dan 3 berikut ini akan diperlihatkan bahwa batas bawah

ekspo-nen titik dari digraph dwiwarna primitif S2(2) adalah expS₂(2)(vk) ≥ n−2 +k untuk

k = 2,3, ..., n.

2. Kasus k = 2

Pilih y∗ _{= v2, path p}

vk,v2 dari titik vk ke titik v2 adalah (k −3 + n,1)-path

persamaan (5) diperoleh

u0 =b(γ2)r(pk,y∗)−r(γ2)(pk,y∗) = 1(k−3 +n)−(n−1)1 =k−2. (17)

Selanjutnya pilih x∗ _{= v1, path p}

vk,v1 dari titik vk ke titik v1 adalah (k −2,1)-path

dengan r(pk,x∗) =k−2 danr(bk,x∗) = 1. Menggunakan (k−2,1)-path dan persamaan

(6) diperoleh

v0 =r(Cγ1)b(pk,x∗)−b(γ1)r(pk,x∗) = 1(1)−0(k−2) = 1. (18)

Menggunakan Lemma (2.7.1), persamaan (17) dan (18) diperoleh



 g

h 

≥M   u0 v0  =  

1 n−1

0 1



 

 k−2

1 

= 



n−3 +k

1



. (19)

Sehingga

exp_S(2)

2 (vk)≥ n−2 +k (20)

untuk k = 2.

3. Kasus 3≤k ≤n

Pilih y∗ _{= v2, untuk setiap titikv}

k di S₂(2), path pk,v2 dari titik vk ke titik v2 adalah (k−2,0)-path dengan r(pk,y∗) =k−2 dan r(p_k,y∗) = 0. Menggunakan path tersebut

dan persamaan (5) diperoleh

u0 =b(γ2)r(pk,y∗)−r(γ2)b(p_k,y∗) = 1(k−2)−(n−1)0 =k−2. (21)

Selanjutnya pilihx∗ _{=v1, untuk setiap titikv}

k diS₂(2), path pk,v1 dari titikvk ke titik v1 adalah (k−2,1)-path dengan r(pk,x∗) =k−2 danr(p_k,x∗) = 1. Menggunakan path

tersebut dan persamaan (6) diperoleh

v0 =r(γ1)b(pk,x∗)−b(γ1)r(p_k,x∗) = 1(1)−0(k−2) = 1. (22)

Oleh Lemma (2.7.1), persamaan (21) dan (22) diperoleh



 g

h 

≥M   u0 v0  =  

1 n−1

0 1



 

 k−2

1 

= 



n−3 +k

1



38

Sehingga

exp_S(2)

2 (vk)≥ n−2 +k (24)

untuk semua k = 3,4, ..., n.

Dengan menggabungkan persamaan (20) dan (24) dapat disimpulkan bahwa

exp_S(2)

2 (vk)≥ n−2 +k (25)

untuk semua k = 2,3, ..., n.

Selanjutnya diperlihatkan bahwa batas atas eksponen titik dari digraph

dwi-warna primitif S₂(2) adalah exp_S(2)

2 (vk) ≤ n − 2 + k untuk semua k = 2,3, ..., n. Pertama akan diperlihatkan exp_S(2)

2 (v2) = n. Menggunakan persamaan tersebut dan Prosisi (2.7.1) akan diperlihatkan batas atas eksponen titik digraph dwiwarna

prim-itif S₂(2) untuk k = 2,3, ..., n. Dari persamaan (25) diketahui bahwa untuk k = 2, exp_S(2)

2 (v2) ≥ n. Dengan demikian tinggal diperlihatan expS (2)

2 (v2) ≤ n. Menggu-nakan persamaan (23) akan diperlihatkan bahwa untuk setiap i = 1,2, ..., n terdapat

path dari titik v2 ke titikvi dengan komposisi n−1 arc merah dan 1 arc biru. Untuk

itu cukup perlihatkan bahwa sistem persamaan

M   x1 x2  +  

r(p2,i)

b(p2,i)



= 

 n−1

1 

 (26)

punya solusi bulat tak negatif, yaitu x1 ≥0 dan x2 ≥0.

Misalkan pathp2,i adalah path dariv2 kevi, i= 1,2, ..., n. Karena S₂(2) adalah

primitif, maka matriks cycle M adalah invertible dengan M−1 ₌





1 1−n

0 1



,

se-hingga solusi dari persamaan (26) adalah

  x1 x2  =  

1 1−n

0 1



 



n−1−r(p2,i)

1−b(p2,i)



= 



(n−1)b(p2,i)−r(p2,i)

1−b(p2,i)



Jikai= 1, pathp2,i dari titikv2ke titikvi adalah (0,1)-path denganr(p2,i) = 0

dan b(p2,i) = 1, diperoleh x1 = n − 1 > 0 dan x2 = 0. Perhatikan bahwa

un-tuk sembarang titik vi, i = 2,3, ..., n, terdapat suatu path p2,i dari titik v2 ke titik

vi dengan 1 ≤ r(p2,i) ≤ n − 1 dan b(p2,i) = 1 yang mengakibatkan x1 ≥ 0 dan

x2 = 0. Berdasarkan hasil tersebut dapat disimpulkan bahwa persamaan (26) punya

solusi bulat tak negatif dan Prosisi (2.7.2) menjamin bahwa exp_S(2)

2 (v2) ≤n. Karena exp_S(2)

2 (v2)≥ndan expS (2)

2 (v2)≤ n, maka expS (2)

2 (v2) =n. Untuk setiapk = 2,3, ..., n, diketahui bahwa jarak dari titik vk ke titikv2 adalah d(vk, v2) =k−2, Prosisi (2.7.1)

menjamin bahwa exp_S(2)

2 (vk)≤expS (2)

2 (v2) +d(vk, v2), sehingga diperoleh

exp_S(2)

2 (vk)≤ n−2 +k (27)

untuk semua k = 2,3, ..., n.

Menggabungkan persamaan (25) dan (27) dapat disimpulkan bahwa eksponen

titik dari S₂(2) adalah exp_S(2)

2 (vk) =n−2 +k untuk semua k = 2,3, ..., n.

Dari kasus 1, 2 dan 3 dapat disimpulkan bahwa ekponen titik dari digraph

dwiwarna primitif S₂(2) adalah exp_S(2)

2 (vk) =n−2 +k untuk semua k= 1,2, ..., n.

Lemma 4.2 AndaikanS₂(2)adalah digraph dwiwarna primitif tipe II, makaexp_S(2)

2 (vk) = n−1 +k untuk semua k = 1,2, ..., n.

Bukti. Berikut ini diperlihatkan bahwa eksponen titik dari digraph dwiwarna prim-itif S₂(2) adalah exp_S(2)

2 (vk) = n −1 +k untuk k = 1,2, ..., n. Karena path merah dengan panjang n−1 adalah path vn→vn−1 →vn−2 → · · · →v2 →v1, pilihx∗ =vn

dan y∗ _{= v1 sebagai titik awal dan titik akhir. Akan digunakan path p}

k,y∗ dari v_k

ke vy∗ untuk menentukan nilai u0 pada persamaan (5), dan path p_k,x∗ dari v_k ke v_x∗

untuk menentukan nilai v0 pada persamaan (6). Pertama akan diperlihatkan batas

bawah eksponen titik dari S₂(2), yakni exp_S(2)

40

1. Kasus k = 1

Dengan memilih y∗ _{= v1, path p}

vk,v1 dari titik vk ke titik v1 adalah (1,0)-path dan

(k+n−2,1)-path. Menggunakan (k+n−2,1)-pathpvk,v1 dan persamaan (5) diperoleh

u0 =b(γ2)r(pk,y∗)−r(γ2)b(p_k,y∗) = 1(k+n−2)−(n−1)1 =k−1. (28)

Menggunakan (1,0)-path dan persamaan (5) diperoleh

u0 =b(γ2)r(pk,y∗)−r(γ2)b(pk,y∗) = 1(1)−(n−1)0 = 1. (29)

Karena batas bawah tercapai bila nilai u0 kecil, maka dari persamaan (28) dan (29)

pilihu0 =k−1.

Selanjutnya pilihx∗ _=v

n, pathpvk,vn dari titikvkke titikvnadalah (0,1)-path.

Menggunakan (0,1)-path dan persamaan (6) diperoleh

v0 =r(γ1)b(pk,x∗)−b(γ1)r(p_k,x∗) = 1(1)−0(0) = 1. (30)

Oleh Lemma (2.7.1), persamaan (28) dan (30) diperoleh



 g

h 

≥M 

 u0

v0 

= 



1 n−1

0 1



 

 k−1

1 

= 



n−2 +k

1



.

Sehingga

exp_S(2)

2 (vk) =g+h≥n−1 +k (31)

untuk k = 1.

2. Kasus 2≤k ≤n

Dengan cara yang sama seperti kasus 1, pilih y∗ _{= v1, untuk setiap titik v}

k di S