Di SMP Negeri 11 Depok
Skripsi
Diajukan Kepada Fakultas Ilmu Tarbiyah dan Keguruan
Untuk Memenuhi Salah Satu Syarat Mencapai Gelar Sarjana Pendidikan
oleh
Ratu Rahma Felasiva
(1110017000048)
JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS ILMU TARBIYAH DAN KEGURUAN
UNIVERSITAS ISLAM NEGERI SYARIF HIDAYATULLAH
i
Matematik Siswa”. Skripsi Jurusan Pendidikan Matematika Fakultas Ilmu Tarbiyah dan Keguruan Universitas Islam Negeri Syarif Hidayatullah Jakarta, Desember 2014.
Tujuan penelitian ini adalah untuk mendeskripsikan kemampuan koneksi matematik siswa yang diajarkan menggunakan strategi pembelajaran REACT dengan teknik scaffolding dan yang diajarkan dengan pembelajaran konvensional serta menganalisis perbedaan kemampuan koneksi matematik antara siswa yang diajarkan menggunakan strategi REACT dengan teknik scaffolding dan siswa yang diajarkan dengan pembelajaran konvensional. Penelitian ini dilaksanakan di SMP Negeri 11 Depok pada Tahun Ajaran 2014/2015. Metode yang digunakan adalah metode quasi eksperimen denganPosttest Only Control Design. Penelitian ini melibatkan 88 siswa sebagai sampel yang ditentukan dengan teknik cluster random sampling. Pengumpulan data setelah perlakuan dilakukan dengan tes kemampuan koneksi matematik siswa.
Hasil penelitian menunjukkan bahwa kemampuan koneksi matematik siswa yang diajar menggunakan strategi pembelajaran REACT dengan teknik scaffoldingmencapai nilai rata-rata 67,98 dengan nilai kemampuan koneksi antar topik matematik sebesar 59,47, nilai kemampuan koneksi matematik dengan mata pelajaran lain sebesar 71,59 dan nilai kemampuan koneksi matematik dengan kehidupan sehari-hari sebesar 76,42. Sedangkan, kemampuan koneksi matematik siswa yang diajar secara konvensional mencapai nilai rata-rata 57,50 dengan nilai kemampuan koneksi antar topik matematik sebesar 56,06, nilai kemampuan koneksi matematik dengan mata pelajaran lain sebesar 58,33, dan nilai kemampuan koneksi matematik dengan kehidupan sehari-hari sebesar 60,23. Berdasarkan pengujian hipotesis diperoleh kesimpulan bahwa kemampuan koneksi matematik siswa yang diajarkan menggunakan strategi pembelajaran REACT dengan teknikscaffoldinglebih tinggi dari pada siswa yang diajar dengan pembelajaran konvensional.
ii
ABSTRACT
RATU RAHMA FELASIVA (1110017000048), “The Effects of REACT Learning Strategy Using Scaffolding Techniques Toward Student’s Mathematical Connection Ability”. Thesis Department of Mathematics Education, Faculty of Tarbiya and Teachers Training, Syarif Hidayatullah State Islamic University Jakarta, December 2014.
The purpose of this research is to describe the mathematical connection ability of students who are taught by REACT learning strategy using scaffolding techniques and conventional learning and to analyze the difference of mathematical connection ability between students who are taught by REACT learning strategy using scaffolding techniques and students taught by conventional learning. This research was conducted at SMPN 11 Depok, for academic year 2014/2015. The method used in this research is quasi experimental method with Posttest Only Control Design. The research involve 88 students as sample which are determined by cluster random sampling technique. The data collection after treatment conducted by the test of mathematical connection ability.
The results of this research revealed that the mathematical connections ability of student who are taught by REACT learning strategy using scaffolding techniques has mean score 67,98, with the score of connections between mathematical topics ability is 59,47, score of connections to other school subjects ability is 71,59, and score of connections to the real world ability is 76,42. While the mathematical connections ability of students who are taught by conventional learning has mean score 57,50, with the score of connections between mathematical topics ability is 56,06, score of connections to other school subjects ability is 58,33, and score of connections to the real world ability is 60,23. Based on the hypothesis test results, it is concluded that the mathematical connections ability of students who are taught by REACT learning strategy higher than students who are taught by conventional learning.
iii
Alhamdulillah, puji syukur penulis panjatkan kehadirat Allah S.W.T yang telah memberikan karunia, nikmat, kemudahan dan kekuatan sehingga penulis dapat menyelesaikan skripsi ini dengan sebaik-baiknya. Shalawat dan salam senantiasa kami curahkan kepada Nabi Muhammad SAW. beserta seluruh keluarga, sahabat, dan para pengikutnya yang senantiasa mengikuti ajarannya sampai akhir zaman.
Selama penulisan skripsi ini, penulis menyadari sepenuhnya bahwa kemampuan dan pengetahuan penulis sangat terbatas. Namun, berkat dorongan serta masukan-masukan yang positif dari berbagai pihak sangat membantu penulis dalam menyelesaikan skripsi ini. Oleh sebab itu penulis mengucapkan terimakasih kepada: 1. Ibu Nurlena Rifa’i, M.A., Ph.D., Dekan Fakultas Ilmu Tarbiyah dan Keguruan
UIN Syarif Hidayatullah Jakarta.
2. Bapak Dr. Kadir, M.Pd., Ketua Jurusan Pendidikan Matematika Fakultas Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta.
3. Bapak Abdul Muin, S.Si., M.Pd., Sekretaris Jurusan Pendidikan Matematika Fakultas Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta.
4. Bapak Otong Suhyanto, M.Si. Dosen Pembimbing I yang selalu memberikan bimbingan, kesabaran, pengarahan, waktu, nasihat dan semangat dalam penulisan skripsi ini.
5. Bapak Drs. Dindin Sobiruddin, M.Kom., Dosen Pembimbing II yang selalu memberikan bimbingan, kesabaran, pengarahan, waktu, nasihat dan semangat dalam penulisan skripsi ini.
iv
7. Seluruh Dosen Jurusan Pendidikan Matematika UIN Syarif Hidayatullah Jakarta yang telah memberikan ilmu pengetahuan serta bimbingan kepada penulis selama mengikuti perkuliahan, semoga ilmu yang telah Bapak dan Ibu berikan mendapatkan keberkahan dari Allah SWT.
8. Staf Fakultas Tarbiyah dan Keguruan dan Staf Jurusan Pendidikan Matematika UIN Syarif Hidayatullah Jakarta yang telah memberi kemudahan dalam pembuatan surat-surat serta sertifikat.
9. Bapak Iskandar Salech, S.Pd., M.M., kepala SMPN 11 Depok, yang telah memberikan izin untuk melakukan penelitian.
10. Ibu Erna Suzana, S.Pd. dan Ibu Juliana, S.Pd., selaku guru matematika di SMPN 11 Depok.
11. Siswa dan siswi kelas VII SMPN 11 Depok, khususnya kelas VII.6 dan VII.7 yang telah bersikap kooperatif selama penulis mengadakan penelitian.
12. Keluarga tercinta Ayahanda Drs. H. Makhrus, M.Pd.I dan Ibunda Dra. Hj. Mustaniroh yang tak henti-hentinya mendoakan, melimpahkan kasih sayang dan memberikan dukungan moril dan materil kepada penulis. Terima kasih Yah, Bu, sudah begitu sabar mendidik fela. Semoga fela bisa membuat ayah dan ibu bangga. Kakak dr. Nadia Nurotul Fuadah dan kakak ipar Ahmad Najih Kholil,Lc.,MH. yang sudah memberikan contoh yang baik dan selalu mendorong penulis untuk tetap semangat dalam mengejar dan meraih cita-cita.
v
Semoga Allah melimpahkan rahmat dan karunia-Nya atas segala jasa dan amal kebaikan yang diberikan kepada penulis.
Demikianlah skripsi ini disusun dengan sebaik-baiknya, namun penulis menyadari bahwa dalam pembuatan skripsi ini masih ditemui kekurangan dan kelemahan. Penulis berharap semoga skripsi ini dapat memberikan manfaat yang sebesar-besarnya baik kepada penulis maupun pembaca.
Jakarta, Desember 2014
vi
DAFTAR ISI
ABSTRAK ... i
ABSTRACT... ii
KATA PENGANTAR ... iii
DAFTAR ISI... vi
DAFTAR TABEL ... ix
DAFTAR GAMBAR ... x
DAFTAR DIAGRAM ... xi
DAFTAR LAMPIRAN ... xii
BAB I PENDAHULUAN... 1
A. Latar Belakang Masalah... 1
B. Identifikasi Masalah ... 7
C. Pembatasan Masalah ... 7
D. Perumusan Masalah... 8
E. Tujuan Penelitian... 8
F. Manfaat Penelitian... 9
BAB II KAJIAN TEORI, KERANGKA BERPIKIR DAN HIPOTESIS PENELITIAN ... 10
A. Kajian Teori... 10
1. Kemampuan Koneksi Matematik... 10
2. Strategi Pembelajaran REACT dengan Teknik Scaffolding... 16
a. Strategi Pembelajaran REACT ... 16
b. TeknikScaffolding... 21
1) Teori Vigotsky ... 21
2) TeknikScaffolding... 23
c. Tahapan Strategi Pembelajaran REACT dengan Teknik ScaffoldingTerhadap Kemampuan Koneksi Matematik ... 26
vii
A. Tempat dan Waktu Penelitian ... 35
B. Populasi dan Sampel ... 35
C. Metode dan Desain Penelitian... 35
D. Teknik dan Instrumen Pengumpulan Data ... 36
E. Uji Instrumen Penelitian... 39
F. Teknik Analisis Data ... 43
G. Hipotesis Statistik... 47
BAB IV HASIL PENELITIAN DAN PEMBAHASAN... 48
A. Deskripsi Data ... 48
1. HasilPosttestKemampuan Koneksi Matematik Siswa ... 48
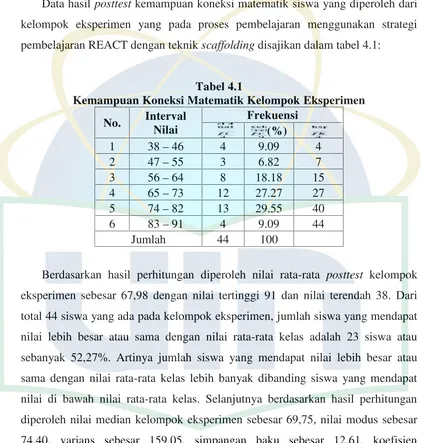
a. HasilPosttestKemampuan Koneksi Matematik Siswa Kelompok Eksperimen... 49
b. HasilPosttestKemampuan Koneksi Matematik Siswa Kelompok Kontrol ... 50
2. Kemampuan Koneksi Matematik Siswa Berdasarkan Indikator Koneksi Matematik... 54
a. Kemampuan Koneksi Matematik Siswa Kelompok Eksperimen Berdasarkan Indikator Koneksi Matematik ... 54
b. Kemampuan Koneksi Matematik Siswa Kelompok Kontrol Berdasarkan Indikator Koneksi Matematik ... 56
c. Perbandingan Kemampuan Koneksi Matematik Kelompok Eksperimen dan Kelompok Kontrol Berdasarkan Indikator Koneksi Matematik ... 57
B. Hasil Pengujian Prasyarat Analisis ... 60
1. Uji Normalitas ... 60
a. Uji Normalitas Kelompok Eksperimen ... 60
viii
2. Uji Homogenitas... 61
C. Pengujian Hipotesis... 62
D. Pembahasan Hasil Penelitian ... 64
E. Keterbatasan Penelitian ... 79
BAB V KESIMPULAN DAN SARAN ... 81
A. Kesimpulan... 81
B. Saran... 82
ix
Tabel 2.1 Tujuan dan PertanyaanScaffolding... 25
Tabel 2.2 Tahapan Strategi Pembelajaran REACT dengan TeknikScaffolding... 27
Tabel 3.1 Desain Penelitian ... 36
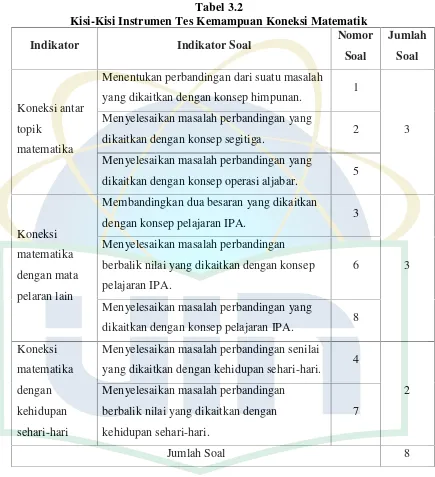
Tabel 3.2 Kisi-kisi Intstrumen Tes Kemampuan Koneksi Matematik ... 37
Tabel 3.3 Pedoman Penskoran Tes Kemampuan Koneksi Matematik... 38
Tabel 3.4 Klasifikasi Indeks Reliabilitas Soal ... 40
Tabel 3.5 Klasifikasi Daya Pembeda Soal... 41
Tabel 3.6 Klasifikasi Tingkat Kesukaran Soal ... 42
Tabel 3.7 Rekapitulasi Hasil Uji Instrumen Penelitian ... 42
Tabel 4.1 Kemampuan Koneksi Matematik Kelompok Eksperimen ... 49
Tabel 4.2 Kemampuan Koneksi Matematik Kelompok Kontrol... 50
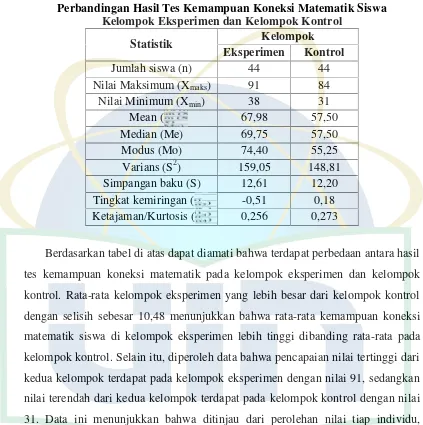
Tabel 4.3 Perbandingan Hasil Tes Kemampuan Koneksi Matematik Siswa Kelompok Eksperimen dan Kelompok Kontrol... 52
Tabel 4.4 Kemampuan Koneksi Matematik Siswa Kelompok Eksperimen Berdasarkan Indikator Koneksi Matematik ... 54
Tabel 4.5 Kemampuan Koneksi Matematik Siswa Kelompok Kontrol Berdasarkan Indikator Koneksi Matematik ... 56
Tabel 4.6 Perbandingan Kemampuan Koneksi Matematik Siswa Kelompok Eksperimen dan Kontrol Berdasarkan Indikator Koneksi Matematik ... 58
Tabel 4.7 Rekapitulasi Hasil Uji Normalitas ... 61
Tabel 4.8 Rekapitulasi Hasil Uji Homogenitas ... 62
x
DAFTAR GAMBAR
Gambar 4.1 Kurva Uji Perbedaan Data Kelompok Eksperimen dan
Kelompok Kontrol ... 63 Gambar 4.2 Pekerjaan Siswa Kelompok Eksperimen Pada TahapRelating. 65 Gambar 4.3 Pekerjaan Siswa Kelompok Eksperimen Pada Tahap
Experiencing... 67 Gambar 4.4 Pekerjaan Siswa Kelompok Eksperimen Pada Tahap
Applying... 68 Gambar 4.5 Kegiatan Pembelajaran di Kelompok Eksperimen ... 69 Gambar 4.6 Pekerjaan Siswa Kelompok Eksperimen Pada Tahap
Transferring... 70 Gambar 4.7 Jawaban soalposttestnomor 2 yang benar pada (i)
kelompok eksperimen dan (ii) kelompok kontrol ... 72 Gambar 4.8 Jawaban soalposttestnomor 2 yang kurang tepat pada (i)
kelompok eksperimen dan (ii) kelompok kontrol ... 73 Gambar 4.9 Jawaban soalposttestnomor 8 yang benar pada (i)
kelompok eksperimen dan (ii) kelompok kontrol ... 75 Gambar 4.10 Jawaban soalposttestnomor 8 yang kurang tepat pada (i)
kelompok eksperimen dan (ii) kelompok kontrol ... 75 Gambar 4.11 Jawaban soalposttestnomor 7 yang benar pada (i)
kelompok eksperimen dan (ii) kelompok kontrol ... 77 Gambar 4.12 Jawaban soalposttestnomor 7 yang kurang tepat pada (i)
xi
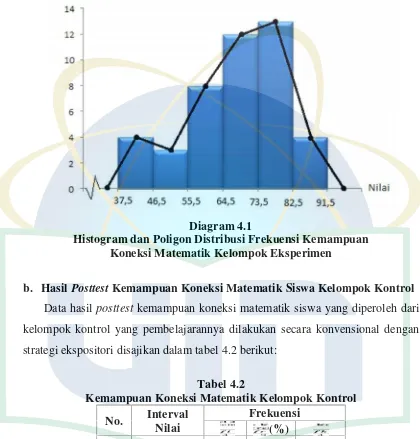
Diagram 4.1 Histogram dan Poligon Distribusi Frekuensi Kemampuan
Koneksi Matematik Kelompok Eksperimen... 50 Diagram 4.2 Histogram dan Poligon Distribusi Frekuensi Kemampuan
Koneksi Matematik Kelompok Kontrol ... 51 Diagram 4.3 Perbandingan Sebaran Data Hasil Tes Kemampuan
Koneksi Matematik Siswa Kelompok Eksperimen dan
Kelompok Kontrol ... 53 Diagram 4.4 Perbandingan Kemampuan Koneksi Matematik Siswa
Kelompok Eksperimen dan Kontrol Berdasarkan Indikator
xii
DAFTAR LAMPIRAN
Lampiran 1 Hasil Wawancara Guru... 86
Lampiran 2 Rencana Pelaksanaan Pembelajaran Kelompok Eksperimen .... 88
Lampiran 3 Rencana Pelaksanaan Pembelajaran Kelompok Kontrol... 93
Lampiran 4 Lembar Kerja Siswa (LKS) Kelompok Eksperimen ... 97
Lampiran 5 Lembar Kerja Siswa (LKS) Kelompok Kontrol... 136
Lampiran 6 Kisi-kisi Uji Coba Instrumen Kemampuan Koneksi Matematik Siswa ... 151
Lampiran 7 Uji Coba Instrumen Kemampuan Koneksi Matematik Siswa .. 154
Lampiran 8 Kunci Jawaban Uji Coba Instrumen Kemampuan Koneksi Matematik Siswa ... 156
Lampiran 9 Hasil Uji Coba Instrumen Tes Kemampuan Koneksi Matematik Siswa ... 165
Lampiran 10 Langkah-langkah Perhitungan Uji Validitas ... 166
Lampiran 11 Hasil Uji Validitas ... 168
Lampiran 12 Langkah-langkah Perhitungan Uji Reliabilitas... 170
Lampiran 13 Hasil Uji Reliabilitas ... 171
Lampiran 14 Langkah-langkah Perhitungan Uji Tingkat Kesukaran ... 173
Lampiran 15 Hasil Uji Tingkat Kesukaran Soal ... 174
Lampiran 16 Langkah-langkah Perhitungan Uji Daya Pembeda Soal... 176
Lampiran 17 Hasil Uji Daya Pembeda Soal ... 177
Lampiran 18 Kisi-kisi Instrumen Tes Kemampuan Koneksi Matematik ... 178
Lampiran 19 Instrumen Tes Kemampuan Koneksi Matematik Siswa... 181
Lampiran 20 Kunci Jawaban Instrumen Tes Kemampuan Koneksi Matematik ... 184
xiii
Kelompok Eksperimen ... 194
Lampiran 24 Perhitungan Daftar Distribusi Frekuensi, Mean, Median, Modus, Varians, Simpangan Baku, Kemiringan dan Kurtosis Kelompok Kontrol ... 199
Lampiran 25 Skor Kemampuan Koneksi Matematik Kelompok Eksperimen ... 204
Lampiran 26 Skor Kemampuan Koneksi Matematik Kelompok Kontrol... 206
Lampiran 27 Perhitungan Uji Normalitas Kelompok Eksperimen ... 208
Lampiran 28 Perhitungan Uji Normalitas Kelompok Kontrol... 210
Lampiran 29 Perhitungan Uji Homogenitas ... 212
Lampiran 30 Perhitungan Uji Hipotesis Statistik... 213
Lampiran 31 Tabel Nilai Koefisien Korelasi Product Moment Pearson ... 215
Lampiran 32 Tabel Nilai Kritis Distribusi Kai Kuadrat (Chi Square)... 217
Lampiran 30 Tabel Nilai Kritis Distribusi F ... 219
1
BAB I
PENDAHULUAN
A. Latar Belakang
Matematika merupakan salah satu bidang ilmu yang tercakup dalam kurikulum pembelajaran baik di tingkat pendidikan dasar, menengah, hingga tingkat pendidikan tinggi. Hal ini disebabkan matematika merupakan salah satu ilmu dasar yang terus berkembang pesat, baik dalam hal materi maupun pemanfaatannya. Matematika tidak hanya berfungsi sebagai ilmu, namun juga sebagai alat, bahasa, dan pola pikir sehingga matematika memiliki peran yang besar dalam perkembangan peradaban, ilmu pengetahuan dan teknologi, serta sumber daya manusia. Bahkan, di dalam kitab Al-Qur’an, tertulis firman Allah yang menggambarkan bahwa matematika memiliki kaitan dan manfaat dengan berbagai hal, seperti dengan alam semesta ataupun dengan kehidupan bermasyarakat. Salah satunya terdapat pada Q.S. Al-Baqarah ayat 267 yang menggambarkan kaitan dan fungsi matematika dalam ajaran Agama dan kehidupan bermasyarakat berikut ini:
ْا
ْاﻮ ُﻘ ِﻔ ﻧ َأ
ﻦ ِﻣ
ِﺖ
ﺎ َﻣ
ﺎ َﻨ
ﻢ ُﻜ َﻟ
َﻦ ﱢﻣ
َﻻ َو
َن ﻮ ُﻘ ِﻔ ﻨ ُﺗ
ﻢ ُﺘ
ِﺑ
ن َأ
ْاﻮ ُﻀ ِﻤ
َو
ْا
ﱠن َأ
ﱞﻲ ِﻨ َﻏ
٢ ٦ ٧
Yang artinya:267. Hai orang-orang yang beriman, nafkahkanlah (di jalan allah) sebagian dari hasil usahamu yang baik-baik dan sebagian dari apa yang Kami keluarkan dari bumi untuk kamu. Dan janganlah kamu memilih yang buruk-buruk lalu kamu menafkahkan daripadanya, padahal kamu sendiri tidak mau mengambilnya melainkan dengan memincingkan mata terhadapnya. Dan ketahuilah, bahwa Allah Maha Kaya lagi Maha Terpuji.
secara menyeluruh serta dapat mengimplementasikannya dalam situasi yang relevan. Hal ini dapat dicapai melalui kemampuan koneksi matematik yang baik, sehingga memungkinkan siswa untuk dapat melakukan koneksi antara ide matematik dengan ide lainnya.
Standar isi mata pelajaran matematika yang dikeluarkan Depdiknas pada tahun 2006 menyatakan bahwa pembelajaran matematika memiliki lima tujuan, yaitu1:
1. Memahami konsep matematika, menjelaskan keterkaitan antarkonsep dan mengaplikasikan konsep atau algoritma, secara luwes, akurat, efisien, dan tepat, dalam pemecahan masalah.
2. Menggunakan penalaran pada pola dan sifat, melakukan manipulasi matematika dalam membuat generalisasi, menyusun bukti, atau menjelaskan gagasan dan pernyataan matematika.
3. Memecahkan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh.
4. Mengomunikasikan gagasan dengan simbol, tabel, diagram, atau media lain untuk memperjelas keadaan atau masalah.
5. Memiliki sikap menghargai kegunaan matematika dalam kehidupan, yaitu memiliki rasa ingin tahu, perhatian, dan minat dalam mempelajari matematika, serta sikap ulet dan percaya diri dalam pemecahan masalah.
Poin pertama dari uraian di atas menyebutkan bahwa siswa diharapkan dapat memahami konsep matematika, menjelaskan keterkaitan antar konsep dan mengaplikasikan konsep atau algoritma. Matematika adalah ilmu yang tersusun dari berbagai ide, konsep, dan aturan yang saling berhubungan. Unsur-unsur dalam matematika tersebut tersusun secara spiral dan hirarkis dimana saat mempelajari suatu konsep perlu memperhatikan konsep lain yang telah dipelajari sebelumnya. Hal ini menunjukkan bahwa kegiatan menghubungkan konsep-konsep matematika tidak dapat dilepaskan dari pembelajaran matematika. Kemampuan koneksi matematik yang baik akan membantu siswa dalam membangun pemahaman matematika yang baik pula. Oleh sebab itu kemampuan koneksi matematik menjadi salah satu tujuan utama pembelajaran matematika di sekolah.
1
3
Selain itu, siswa juga diharapkan dapat menghargai kegunaan matematika. Ketika siswa memiliki kemampuan koneksi matematik yang baik, ia akan menyadari bahwa matematika dapat ia gunakan untuk menyelesaikan masalah yang ia temui dalam kehidupan sehari-hari, seperti saat ia melakukan kegiatan jual beli, melakukan kegiatan organisasi, dan hal-hal lainnya. Dengan ini, siswa dapat melihat matematika secara menyeluruh dan menyadari bahwa matematika memiliki daya guna yang nyata. Hal ini sejalan dengan pernyataan Kline (1973) bahwa matematika bukanlah pengetahuan menyendiri yang dapat sempurna karena dirinya sendiri, tetapi adanya matematika itu terutama untuk membantu manusia dalam memahami dan menguasai permasalahan sosial, ekonomi, dan alam.2
Kemampuan koneksi matematik juga disebutkan oleh National Council of Teachers of Mathematics atau NCTM sebagai tujuan mendasar dalam belajar matematika, atau yang lebih dikenal dengan istilah daya matematis. Ada lima kemampuan yang merupakan daya matematis, yaitu pemecahan masalah (problem solving), penalaran (reasoning), komunikasi (communication), koneksi (connections), dan representasi (representation).3 Hal ini menunjukkan bahwa kemampuan koneksi matematik patut dijadikan perhatian dalam pembelajaran matematika.
Di balik fakta pentingnya matematika dan kemampuan koneksi matematik bagi siswa, kenyataan yang ada justru menunjukkan hasil sebaliknya. Berbagai data menunjukkan bahwa prestasi matematika siswa Indonesia di kancah internasional kian memprihatinkan. Salah satunya tampak dari penelitian yang dilakukan Programme for International Student Assessment (PISA) pada tahun 2012. Penelitian tersebut dilakukan untuk mengukur kecakapan anak-anak usia 15 tahun dalam mengimplementasikan masalah-masalah di kehidupan nyata. Hasilnya, Indonesia berada pada peringkat ke-64 dari 65 negara yang berpartisipasi dengan perolehan skor matematika sebesar 375, cukup jauh di
2
Erman Suherman, Strategi Pembelajaran Matematika Kontemporer, (Bandung: JICA UPI, 2001), h. 19.
3
bawah skor rata-rata yaitu sebesar 494.4 Peringkat ini menunjukkan bahwa kemampuan siswa Indonesia dalam menerapkan konsep matematika yang dipelajarinya ke dalam masalah di kehidupan nyata masih rendah. Kemampuan menerapkankan konsep matematika ke dalam kehidupan nyata merupakan salah satu indikator kemampuan koneksi matematik, sehingga pencapaian ini menjadi salah satu bukti bahwa kemampuan koneksi matematik siswa Indonesia tergolong rendah.
Sebelumnya, penelitian mengenai kemampuan koneksi matematik telah dilakukan Sugiman pada tahun 2008. Penelitian tersebut menunjukkan bahwa kemampuan koneksi matematik siswa sekolah menengah tergolong rendah, yakni hanya 53,5%. Dari persentase tersebut, hanya 63% siswa yang menguasai aspek koneksi inter topik matematika, 41% siswa menguasai aspek koneksi antar topik matematika, 56% siswa menguasai aspek koneksi matematika dengan pelajaran lain, dan 55% siswa menguasai aspek koneksi matematika dengan kehidupan sehari-hari.5
Selain itu, wawancara pra penelitian yang dilakukan pada guru bidang studi matematika di SMPN 11 Depok juga menunjukkan hasil yang kurang memuaskan mengenai kemampuan matematika siswa, termasuk dalam hal kemampuan koneksi matematik siswa. Kesimpulan tersebut didapat dari data yang diperoleh di lapangan, bahwa:
1. Pengetahuan awal/prasyarat siswa kurang, hal ini dapat dilihat dimana saat pembelajaran berlangsung siswa seringkali lupa dengan materi yang telah dipelajari sebelumnya.
2. Sebagian siswa belum mampu menyelesaikan persoalan yang melibatkan lebih dari satu konsep matematika
3. Sebagian besar siswa mengalami kesulitan jika diberikan permasalahan matematika yang berhubungan dengan kehidupan sehari-hari
4
Programme for International Student Assessment, PISA 2012 Results in Focus, (Paris: OECD, 2013), h. 5.
5
5
4. Beberapa siswa masih mendapatkan hasil yang rendah pada evaluasi hasil belajar matematika
Rendahnya kemampuan koneksi matematik yang ditunjukkan berbagai uraian di atas mengindikasikan perlu adanya tindakan responsif guna meningkatkan kemampuan koneksi matematik siswa. Sebelumnya, beberapa upaya untuk meningkatkan kemampuan koneksi matematik telah dilakukan oleh guru, seperti memberikan apersepsi di awal pembelajaran serta memberikan lebih banyak soal-soal latihan. Namun tampaknya upaya tersebut belum memberikan hasil sebagaimana yang diharapkan. Hal ini disebabkan siswa masih diposisikan sebagai objek pembelajaran dan kurang diberikan kesempatan untuk membangun pengetahuan secara mandiri dengan mengaitkan materi dengan pengalaman dan pengetahuan yang dimilikinya. Untuk itu, perlu dicari solusi lain untuk mengatasi masalah tersebut, salah satunya dalam hal perbaikan program pembelajaran.
Di beberapa sekolah, termasuk di sekolah tempat dilaksanakannya penelitian ini, pembelajaran matematika yang bernuansa konvensional masih menjadi “favorit” para guru. Pembelajaran konvensional yang dimaksud adalah pembelajaran yang cenderung menempatkan guru sebagai sumber utama belajar sedangkan siswa sebagai objek pembelajaran. Dalam jangka panjang, hal ini memberikan dampak yang kurang efektif terhadap perkembangan potensi siswa, khususnya dalam hal kemampuan koneksi matematik siswa. Untuk itu, dalam upaya meningkatkan kemampuan koneksi matematik siswa diperlukan program pembelajaran yang dapat mengatasi kelemahan pembelajaran konvensional. Diperlukan pembelajaran yang memberikan siswa kesempatan untuk terlibat aktif dalam kegiatan belajar, mandiri dalam membangun pengetahuan dan membantu siswa melihat hubungan dari konsep yang dipelajari dengan pengalaman yang dimilikinya. Hal ini sebagaimana diungkapkan oleh Bruner yang menyarankan keterlibatan dan keaktifan siswa dalam proses belajar secara penuh dengan mencoba dan melakukannya sendiri.6
Berkenaan dengan hal tersebut, Center of Occupational Research and Development (CORD) mengajukan sebuah strategi pembelajaran bernuansa
6
kontekstual yang disebut strategi REACT.7 Strategi REACT adalah strategi pembelajaran yang melibatkan siswa secara aktif melalui lima bentuk kegiatan yaitu Relating, Experiencing, Applying,Cooperating, dan Transferring. Relating (mengaitkan), yaitu mengaitkan pengetahuan yang akan dipelajari dengan kehidupan nyata atau dengan pengetahuan yang telah dimiliki siswa sebelumnya. Experiencing (mengalami), yaitu belajar melalui berbagai kegiatan yang dijalani siswa secara aktif, sehingga siswa mendapatkan pengalaman dan dapat membangun pengetahuan secara mandiri. Applying (menerapkan), yaitu menerapkan pengetahuan yang telah diperoleh siswa ke dalam permasalahan yang relevan. Cooperating (bekerja sama), yaitu belajar dengan melakukan kolaborasi dengan siswa lain. Transferring (mentransfer), yaitu belajar menerapkan pengetahuan yang telah dimiliki ke dalam konteks atau situasi yang baru.
Dalam menerapkan strategi pembelajaran di kelas, seringkali diperlukan suatu teknik guna membantu pencapaian tujuan pembelajaran. Salah satu teknik yang banyak dipilih adalah teknikscaffolding.Scaffoldingadalah dukungan pembelajar kepada peserta didik untuk membantunya menyelesaikan proses belajar yang tidak dapat diselesaikannya sendiri.8Ketika mempelajari matematika, tidak jarang siswa kesulitan dalam mengenali konsep yang digunakan, terlebih ketika masalah yang diberikan melibatkan lebih dari satu konsep. Untuk itu guru perlu hadir untuk menjalankan perannya sebagai pembimbing dengan memberikan scaffolding.
Pembelajaran menggunakan strategi REACT dengan teknik scaffolding memfasilitasi siswa untuk terlibat dalam berbagai kegiatan belajar seperti mengaitkan, mengalami, menerapkan, bekerja sama, dan mentransfer pelajaran disertai dengan bimbingan yang terstruktur dari guru. Siswa akan dibimbing untuk dapat mengaitkan materi pelajaran dengan pengalaman dan pengetahuan yang dimilikinya serta bagaimana menerapkan pengetahuan yang diperolehnya dalam berbagai situasi sehingga diharapkan dapat turut meningkatkan hasil belajar
7
Agus Suprijono, Cooperative Learning Teori dan Aplikasi PAIKEM, (Yogyakarta: Pustaka Belajar, 2013), h. 83.
8
7
matematika siswa. Hal ini diharapkan dapat meningkatkan kemampuan koneksi matematik siswa. Berdasarkan latar belakang tersebut, maka peneliti tertarik untuk melakukan penelitian dengan judul “Pengaruh Strategi Pembelajaran REACT Dengan Teknik Scaffolding Terhadap Kemampuan Koneksi Matematik Siswa”.
B. Identifikasi Masalah
Berdasarkan latar belakang masalah yang telah diuraikan sebelumnya, maka dapat diidentifikasi permasalahan sebagai berikut:
1. Kemampuan koneksi matematik siswa masih tergolong rendah, misalnya siswa masih menemui kesulitan ketika diberikan masalah matematika yang berkaitan dengan kehidupan sehari-hari serta mengandung lebih dari satu konsep matematika.
2. Siswa sering lupa terhadap materi yang telah dipelajari padahal berkaitan dengan materi yang akan dipelajari selanjutnya.
3. Pembelajaran yang diterapkan di kelas kurang memberikan kesempatan bagi siswa untuk terlibat aktif dalam membangun pengetahuan dan melihat hubungan matematika.
C. Pembatasan Masalah
Untuk memperjelas pemahaman tentang variabel-variabel yang terkait dalam penelitian ini, maka dilakukan pembatasan masalah sebagai berikut:
1. Kemampuan koneksi matematik yang akan diteliti dalam penelitian ini meliputi koneksi antar topik matematika, koneksi antara topik matematika dengan mata pelajaran lain dan koneksi antara topik matematika dengan kehidupan sehari-hari.
mengalami, menerapkan, bekerja sama dan mentransfer pengetahuan disertai dengan bimbingan yang terstruktur.
3. Penelitian ini mengambil fokus pada pokok bahasan Perbandingan.
D. Perumusan Masalah
Rumusan masalah yang akan dibahas pada penelitian ini antara lain:
1. Bagaimana kemampuan koneksi matematik siswa yang dalam pembelajarannya diterapkan strategi pembelajaran REACT dengan teknik Scaffolding?
2. Bagaimana kemampuan koneksi matematik siswa yang dalam pembelajarannya diterapkan pembelajaran konvensional?
3. Apakah kemampuan koneksi matematik siswa yang mendapat pembelajaran menggunakan strategi REACT dengan teknik Scaffolding lebih tinggi dibandingkan siswa yang mendapat pembelajaran konvensional?
E. Tujuan Penelitian
Tujuan dilakukannya penelitian ini antara lain:
1. Mendeskripsikan kemampuan koneksi matematik siswa yang dalam pembelajarannya diterapkan strategi pembelajaran REACT dengan teknik Scaffolding.
2. Mendeskripsikan kemampuan koneksi matematik siswa yang dalam pembelajarannya diterapkan pembelajaran konvensional.
3. Menganalisis perbedaan kemampuan koneksi matematik antara siswa yang mendapat pembelajaran menggunakan strategi pembelajaran REACT dengan teknikscaffoldingdan siswa yang mendapat pembelajaran konvensional.
F. Manfaat Penelitian
9
1. Bagi siswa, mendapatkan pengalaman belajar yang memberinya kesempatan untuk terlibat secara aktif dalam membangun pengetahuan dan memahami hubungan matematika.
2. Bagi guru mata pelajaran matematika, yaitu pembelajaran dengan strategi REACT dengan teknik Scaffolding dapat dijadikan alternatif pembelajaran yang dapat meningkatkan kualitas belajar mengajar di sekolah khususnya dalam hal kemampuan koneksi matematik siswa.
3. Bagi pihak sekolah, yaitu dapat meningkatkan kualitas proses belajar mengajar di sekolah.
10 A. Kajian Teori
1. Kemampuan Koneksi Matematik
Matematika, tentu bukanlah suatu istilah yang asing di masyarakat, mengingat matematika merupakan salah satu mata pelajaran yang wajib dipelajari mulai dari tingkat dasar hingga tingkat perguruan tinggi. Tidak hanya di dunia pendidikan, matematika juga dekat dengan kehidupan nyata. Begitu banyak permasalahan dalam kehidupan nyata seperti dalam bidang fisika, ekonomi, seni, hingga dalam hidup bermasyarakat dapat diselesaikan dengan menggunakan konsep matematika. Hal ini membuat matematika begitu penting karena kehadirannya tidak dapat dipisahkan dari kehidupan.
Istilah matematika berasal dari bahasa Latin mathematica yang diambil dari bahasa Yunani mathematike yang berarti “relating to learning”. Istilah tersebut berakar dari kata mathema yang berarti pengetahuan atau ilmu. Selain itu, istilah mathematikeberkaitan denganmathaneinyang berarti belajar atau berpikir. Istilah mathematikedanmathematicakemudian diadaptasi dalam berbagai bahasa seperti mathematics (Inggris), mathematic (Jerman), mathematique (Perancis), matematico(Itali),matematiceski(Rusia), ataumathematick/wiskunde(Belanda).1 James dan James (1976) dalam Erman mengatakan bahwa matematika adalah ilmu tentang logika mengenai bentuk, susunan, besaran, dan konsep-konsep yang saling berhubungan satu sama lain dengan jumlah yang banyak yang terbagi ke dalam tiga bidang, yaitu aljabar, analisis, dan geometri.2 Sedangkan Johnson dan Rising (1972) dalam Erman mengatakan bahwa matematika adalah pola berpikir, pola mengorganisasikan, pembuktian yang logik, matematika itu adalah bahasa yang menggunakan istilah yang didefinisikan dengan cermat, jelas dan akurat,
1
Erman Suherman, dkk., Strategi Pembelajaran Matematika Kontemporer, (Bandung: JICA UPI, 2001), h. 17.
2
11
representasinya dengan simbol dan padat, lebih berupa bahasa simbol mengenai ide daripada bunyi.3 Berbagai pendapat tersebut menunjukkan betapa bervariasinya definisi dari matematika, namun dapat disimpulkan bahwa matematika adalah ilmu pengetahuan tentang logika mengenai bentuk, susunan, besaran, simbol, dan konsep-konsep yang saling berhubungan dan terorganisasi secara sistematis.
Koneksi berasal dari bahasa Inggris, yaitu connection yang menurut kamus Bahasa Inggris berarti hubungan, sambungan, pertalian atau sangkut-paut. Semua kata tersebut mengandung persamaan makna yaitu menunjukkan adanya keterkaitan antara dua atau beberapa hal. Jika dikaitkan dengan pengertian matematika, maka koneksi matematik dapat diartikan sebagai hubungan matematik.
Kemampuan koneksi matematik disebutkan sebagai salah satu daya matematis oleh National Council of Teachers of Mathematics (NCTM) serta dijadikan salah satu tujuan dasar dalam pembelajaran matematika. Kemampuan koneksi matematik sebagai salah satu daya matematis tersebut adalah kemampuan dalam membuat hubungan matematik. Standar hubungan yang dikemukakan NCTM tersebut memiliki dua arah yang berbeda, yaitu hubungan di dalam dan antar ide matematik serta hubungan matematik dengan dunia nyata dan mata pelajaran lain.4
Sejalan dengan NCTM, Suhenda mengemukakan bahwa kemampuan koneksi matematik adalah kemampuan untuk mengaitkan satu ide atau gagasan dengan ide atau gagasan lain dalam lingkup yang sama atau bidang lain pada lingkup yang lain.5 Jadi, dapat disimpulkan bahwa kemampuan koneksi matematik adalah kemampuan untuk mengaitkan ide matematik dengan ide lain, baik yang terdapat dalam matematika, dalam disiplin ilmu lain, maupun dalam konteks kehidupan nyata.
3
Ibid, h. 19. 4
John A. Van De Walle,Matematika Sekolah Dasar dan Menengah Edisi Keenam, Terj. dariElementary and Middle School Mathematicsoleh Suyono, (Jakarta: Erlangga, 2008), h. 5.
5
Ide mengenai kemampuan koneksi matematik ini merujuk pada kenyataan bahwa meskipun matematika selama ini terkotak-kotak dalam beberapa cabang, sesungguhnya cabang-cabang ilmu tersebut memiliki suatu ikatan dan terintegrasi sehingga membentuk suatu kesatuan yang padu yang disebut matematika. Matematika berperan hampir pada semua aspek kehidupan manusia, sehingga keterkaitan yang dapat dibuat dengan matematika tidak terbatas pada antar konsep yang ada pada matematika itu sendiri, melainkan juga meliputi ide-ide di luar matematika.
Teori yang mendukung kemampuan koneksi matematik adalah dalil pengaitan yang dikemukakan Bruner. Menurut Bruner dalam Ruseffendi, setiap konsep dalam matematika berkaitan dengan konsep lainnya. Begitupula dengan elemen lain dalam matematika, seperti dalil dengan dalil, teori dengan teori, topik dengan topik, dan antar cabang dalam matematika, semuanya saling berkaitan. Karena itulah siswa perlu diberikan kesempatan untuk dapat melihat kaitan-kaitan tersebut agar dapat mencapai keberhasilan dalam belajar matematika.6
Tujuan dari kemampuan koneksi matematik dapat diamati dari urgensi dan manfaat yang dapat diperoleh ketika koneksi matematik ditekankan dalam pembelajaran matematika di sekolah. Salah satunya adalah fenomena di masyarakat yang menganggap matematika sulit untuk dipahami karena banyaknya rumus yang harus dihapal saat mempelajari matematika. Pemahaman dapat didefinisikan sebagai ukuran kualitas dan kuantitas hubungan suatu ide dengan ide yang telah ada.7 Dengan kata lain, pemahaman bergantung pada banyaknya ide yang dimiliki dan kemampuan untuk membuat hubungan antara ide-ide tersebut sehingga menjadi suatu jaringan konsep dan prosedur yang bermakna. Berkaca dari kenyataan ini, kemampuan koneksi matematik menjadi penting untuk dikembangkan, sebab kemampuan koneksi matematik dapat membantu siswa mencapai pemahaman terhadap matematika.
Dengan membuat koneksi matematik antara ide dan konsep yang ada dalam matematika, siswa tidak perlu mengingat terlalu banyak konsep karena informasi
6
Ruseffendi, Pengantar Kepada Membantu Guru Mengembangkan Kompetensinya dalam Pengajaran Matematika untuk Meningkatkan CBSA, (Bandung: Tarsito, 2006), h. 152.
7
13
yang didapat selalu dikaitkan dengan informasi yang telah ia ketahui. Informasi yang saling dikaitkan tersebut kemudian membentuk jaringan yang terdiri dari konsep-konsep yang saling berhubungan dan bukan menjadi potongan-potongan informasi yang terpisah-pisah. Jaringan yang dibentuk tersebut akan tertanam lebih kuat dalam memori dibanding hanya menghapal tanpa membuat suatu hubungan yang bermakna dari ide-ide yang ada. Hal ini secara positif akan meningkatkan ingatan peserta didik terhadap materi yang dipelajarinya.
Sugiman menyatakan bahwa struktur koneksi yang terdapat di antara cabang-cabang matematika memungkinkan siswa melakukan penalaran matematik secara analitik dan sintetik.8 Karena itu, dapat dikatakan bahwa mengembangkan kemampuan koneksi matematik siswa dapat menimbulkan dampak yang positif pula terhadap kemampuan penalaran siswa. Selain itu, konsep-konsep yang disimpan dan membentuk jaringan juga akan membantu siswa dalam melakukan transfer ide-ide ke dalam konteks situasi yang baru. Kemampuan dalam mentransfer pengetahuan yang dimiliki ke dalam berbagai situasi yang relevan sangat dibutuhkan dalam kegiatan pemecahan masalah. Dengan kata lain, kemampuan koneksi matematik turut mengembangkan kemampuan pemecahan masalah siswa.
Pada akhirnya, ketika siswa dapat membuat koneksi dalam mempelajari matematika, siswa akan memahami bahwa matematika bukanlah sekadar setumpukan informasi yang banyak dan tidak berarti. Justru sebaliknya, siswa menyadari bahwa matematika merupakan suatu ilmu yang terdiri dari konsep-konsep yang membentuk kesatuan yang padu. Di samping itu, siswa dapat menyadari bahwa apa yang mereka pelajari bermakna dan memiliki manfaat yang nyata, bukan hanya di sekolah tapi juga di luar sekolah, seperti dalam dunia pekerjaan ataupun dalam kehidupan bermasyarakat.
Kemampuan koneksi matematik dapat diklasifikasikan ke dalam beberapa jenis sebagaimana dikemukakan oleh para pakar. Utari Sumarmo menyatakan sebagai berikut:
8
Kemampuan yang tergolong pada koneksi matematika di antaranya adalah (a) mencari hubungan berbagai representasi konsep dan prosedur, (b) memahami hubungan antar topik matematika, (c) menerapkan matematika dalam bidang lain atau dalam kehidupan sehari-hari, (d) memahami representasi ekuivalen suatu konsep, (e) mencari hubungan suatu prosedur dengan prosedur lain dalam representasi yang ekuivalen, (f) menerapkan hubungan antar topik matematika dan antara topik matematika dengan topik di luar matematika.9
Dalam buku Learning Mathematics in Elementary and Middle Schools dituliskan bahwa terdapat lima kemampuan koneksi matematik yang penting dalam pembelajaran matematika di sekolah, yaitu10:
a. Pengetahuan konseptual dan prosedural b. Berbagai representasi yang berbeda c. Koneksi topik matematika yang berbeda d. Koneksi dengan dunia nyata
e. Koneksi dengan mata pelajaran lain
Menurut NCTM, standar koneksi untuk kelas VI-VIII harus memungkinkan siswa untuk11:
a. Mengenal dan menggunakan koneksi antara ide-ide matematika (Recognize and use connections among mathematical ideas)
b. Memahami bagaimana ide-ide dalam matematika saling berhubungan dan membangun satu sama lain untuk menghasilkan keseluruhan yang padu (Understand how mathematical ideas interconnect and build one another to produce a coherent whole)
c. Mengenal dan menerapkan matematika dalam konteks di luar matematika (Recognize and apply mathematics in contexts outside of mathematics)
Berdasarkan standar koneksi di atas, maka NCTM mengklasifikasikan kemampuan koneksi matematik ke dalam tiga jenis, yaitu12:
9
Utari Sumarmo,Pembelajaran Matematika dalam Rujukan Filsafat, Teori dan Praksis Ilmu Pendidikan, (Bandung: UPI PRESS, 2008), h. 683.
10
W. George Cathcart, Yvonne M. Pothier dan James H. Vance.Learning Mathematics in Elementary and Middle Schools. (Toronto: Pearson Education, 2008), h. 14-15.
11
15
a. Koneksi antar topik matematika
b. Koneksi dengan disiplin ilmu yang lain c. Koneksi dalam kehidupan sehari-hari.
Sejalan dengan pendapat sebelumya, Suhenda menyatakan bahwa kemampuan koneksi matematik dapat ditunjukkan melalui beberapa hal, yaitu13: a. Menghubungkan antara topik atau bahasan matematika dengan topik atau
pokok bahasan matematika yang lainnya
b. Mengaitkan berbagai topik atau pokok bahasan dalam matematika dengan bidang lain dan atau hal-hal yang berkaitan dengan kehidupan sehari-hari.
Meskipun memiliki deskripsi yang berbeda-beda, berbagai pendapat pakar mengenai klasifikasi kemampuan koneksi matematik di atas memiliki satu pandangan yang sama, yakni membagi kemampuan koneksi matematik menjadi tiga macam, yaitu :
a. Koneksi antar topik matematik
b. Koneksi matematik dengan mata pelajaran lain c. Koneksi matematik dengan konteks kehidupan nyata.
Adapun mengenai kemampuan koneksi matematik yang dimaksud dalam penelitian ini meliputi koneksi internal dan eksternal matematik. Koneksi internal yaitu kemampuan koneksi antar topik matematik. Sedangkan koneksi eksternal yaitu kemampuan koneksi matematik dengan mata pelajaran lain dan kemampuan koneksi matematik dengan kehidupan sehari-hari.
a. Kemampuan koneksi antar topik matematik
Sebagaimana yang diungkapkan Bruner dalam teori konektivitas, elemen-elemen dalam matematika memiliki keterkaitan. Kemampuan siswa dalam membuat koneksi antar topik yang terdapat dalam matematika diperlukan untuk menyelesaikan suatu permasalahan matematika. Contohnya adalah keterkaitan yang dapat dibangun melalui materi persamaan kuadrat, barisan dan deret, bangun geometri, dan sebagainya.
12
Gusni Satriawati dan Lia Kurniawati,“Menggunakan Fungsi-Fungsi Untuk Membuat Koneksi-Koneksi Matematik”,Algoritma Jurnal Matematika dan Pendidikan Matematika, vol. 3, 2008, h. 97.
13
b. Kemampuan koneksi matematik dengan mata pelajaran lain
Matematika merupakan ilmu yang memiliki peran ganda yaitu sebagai ratu sekaligus pelayan ilmu. Hal ini menunjukkan bahwa selain berkembang untuk dirinya sendiri sebagai suatu ilmu, matematika ada sebagai alat dalam ilmu pengetahuan lain. Koneksi matematik dengan pelajaran lain menunjukkan bahwa matematika memiliki relevansi dengan pelajaran lain di sekolah sehingga siswa memandang bahwa matematika memiliki daya guna yang lebih. Contohnya adalah keterkaitan yang dapat dibangun antara pelajaran matematika dengan fisika, ekonomi, biologi, dan sebagainya.
c. Kemampuan koneksi matematik dengan kehidupan sehari-hari
Koneksi matematik dengan kehidupan sehari-hari menunjukkan bahwa daya guna matematika tidak hanya terbatas dalam lingkungan sekolah namun juga dalam kehidupan sehari-hari dan kehidupan bermasyarakat. Banyak permasalahan dalam kehidupan sehari-hari yang dapat diselesaikan dengan konsep matematika.
2. Strategi Pembelajaran REACT Dengan TeknikScaffolding
a. Strategi Pembelajaran REACT
Istilah strategi berasal dari bahasa Yunani stratego, yang berarti merencanakan (to plan). Mintzberg dan Waters menyatakan bahwa strategi adalah pola umum tentang keputusan atau tindakan.14 Hardy, Langley, dan Rose mengemukakan bahwastrategy is perceived as a plan or a set of explisit intention preceeding and controlling actions. Artinya, strategi dipahami sebagai rencana atau kehendak yang mendahului dan mengendalikan kegiatan.15 Jadi, strategi dapat dinyatakan sebagai suatu perencanaan yang disusun secara sengaja dalam melakukan kegiatan atau tindakan untuk mencapai tujuan.
Sedangkan mengenai makna pembelajaran, Gagne dan Brigga (1979) mengemukakan bahwa pembelajaran adalah rangkaian peristiwa yang
14
Abdul Majid,Strategi Pembelajaran, (Bandung: Remaja Rosdakarya, 2013), h. 3. 15
17
memengaruhi sehingga proses belajar dapat berlangsung dengan mudah.16 Menurut Oemar Hamalik, pembelajaran adalah suatu kombinasi yang tersusun meliputi unsur-unsur manusiawi, material, fasilitas, perlengkapan, prosedur yang saling memengaruhi dalam mencapai tujuan pembelajaran.17 Jadi, pembelajaran dapat diartikan sebagai rangkaian kegiatan yang terencana yang dapat membantu siswa untuk dapat belajar dengan baik dan mencapai tujuan yang diharapkan.
Strategi yang diterapkan pada pembelajaran disebut strategi pembelajaran. Kemp menyatakan bahwa strategi pembelajaran adalah suatu kegiatan pembelajaran yang harus dikerjakan guru dan peserta didik agar tujuan pembelajaran dapat dicapai secara efektif dan efisien.18 Sedangkan Gerlach dan Ely menjelaskan bahwa strategi pembelajaran adalah cara-cara yang dipilih untuk menyampaikan materi pembelajaran dalam lingkungan pembelajaran tertentu.19 Maka dapat disimpulkan bahwa strategi pembelajaran adalah perencanaan yang berisi rangkaian kegiatan yang dapat membantu proses belajar siswa agar dapat mencapai tujuan pembelajaran yang diharapkan.
Strategi pembelajaran REACT diperkenalkan oleh Center of Occupational Research and Development (CORD). Pembelajaran ini menuntut siswa untuk terlibat secara aktif dalam berbagai kegiatan pembelajaran dengan melakukan, mencoba, mengalami, bekerja sama dan membuat hubungan antara materi pelajaran dengan pengalaman dunia nyata. Dalam prosesnya, guru membantu menyediakan lingkungan belajar yang dapat mendukung berlangsungnya aktivitas siswa tersebut. Dengan strategi ini siswa dibiasakan untuk membentuk pengetahuannya sendiri, bekerja sama, mengetahui hubungan antar materi yang dipelajarinya serta manfaat yang diperolehnya dari mempelajari suatu materi.
Nama dari strategi REACT ini merupakan akronim dari lima komponen yang terdapat di dalamnya, yaitu Relating (mengaitkan), Experiencing (mengalami),
16
Ibid, h. 4. 17
Ibid. 18
Ibid, h. 7. 19
Applying (menerapkan), Cooperating (bekerja sama), dan Transferring (menransfer).20Lima unsur tersebut dijabarkan sebagai berikut:
1) Relating(mengaitkan)
Relating is learning in the context of one’s life experiences or preexisting
knowledge.21Artinya, relatingatau mengaitkan adalah belajar dengan konteks pengalaman hidup seseorang atau dengan pengetahuan yang telah dimiliki sebelumnya. Relating tampak dalam pembelajaran ketika konsep baru yang akan dipelajari dikaitkan dengan pengetahuan yang telah dimiliki siswa sebelumnya atau dengan hal-hal yang akrab dengan kehidupan siswa.Relating dalam pembelajaran diperlukan guna memberikan pemahaman pada siswa mengenai makna yang terkandung dari apa yang ia pelajari.
Dalam menerapkan relating, guru perlu menyediakan lingkungan dimana siswa dapat mengaktifkan memorinya berupa pengetahuan yang telah dimiliki siswa sebelumnya kemudian mengaitkannya dengan pengetahuan baru yang akan dipelajari.Relatingdapat diimplementasikan dalam pembelajaran dengan menggali pengetahuan prasyarat serta memberikan pertanyaan-pertanyaan yang dekat dengan kehidupan siswa untuk mengawali pembelajaran. Selain itu, guru juga perlu memberikan motivasi dengan menyampaikan hubungan antara materi tersebut dengan berbagai hal, baik dalam kehidupan sehari-hari maupun dalam pelajaran lain, sehingga siswa memahami bahwa apa yang akan dipelajarinya memiliki makna dan manfaat.
2) Experiencing(mengalami)
Dalamexperiencing, peserta didik berproses secara aktif dengan hal yang dipelajari dan berupaya melakukan eksplorasi terhadap hal yang dikaji, berusaha menemukan dan menciptakan hal baru dari apa yang dipelajarinya.22 Experiencing diterapkan untuk membantu siswa mendapatkan pengalaman yang relevan dengan pengetahuan yang akan dipelajarinya.
20
Crawford,Teaching Contextually:Reasearch, Rationale, and Techniques for Improving Student Motivation and Achievement in Mathematics and Science, (Texas: CORD, 2001), h. 3.
21 Ibid. 22
19
Berbagai hasil riset menunjukkan bahwa segera terlibat dalam pembelajaran baru, dengan mempraktikkannya, dapat meningkatkan memori pembelajaran tersebut.23 Artinya, dengan siswa terlibat secara aktif dalam berbagai kegiatan belajar, pengetahuan tersebut akan lebih kuat terpatri dalam memori siswa karena siswa tidak hanya menghapal pengetahuan yang sudah ada melainkan mengkonstruksinya sendiri sehingga menjadi informasi yang ia pahami.
Experiencing dapat diterapkan melalui berbagai kegiatan, seperti eksplorasi, percobaan, maupun kegiatan pemecahan masalah yang dapat dikemas dalam bentuk LKS untuk menuntun siswa membangun konsep yang akan dipelajari. Hal ini dapat meningkatkan aktivitas dan kemandirian belajar siswa karena siswa berusaha membangun pengetahuannya dan tidak hanya menerima pengetahuan yang sudah jadi dari guru. Siswa juga dilatih untuk menggunakan akal pikirannya dan memunculkan ide-ide baru dengan mengerahkan pengetahuan yang telah ia miliki.
3) Applying(menerapkan)
Applying adalah belajar dengan menempatkan konsep-konsep untuk digunakan.24 Artinya bagaimana konsep-konsep yang telah dipelajari oleh siswa tidak hanya dihapal melainkan dapat digunakan oleh siswa. Hal ini penting agar siswa memahami bahwa apa yang dipelajarinya selama ini tidak hanya menjadi tumpukan informasi yang tidak bermakna, melainkan dapat digunakan dan diterapkan dalam berbagai hal yang relevan.
Kemampuan siswa dalam menerapkan atau menggunakan konsep dapat terlihat jika siswa dihadapkan pada kegiatan pemecahan masalah atau proyek.25 Untuk itu, guru dapat memotivasi dan melatih siswa untuk dapat menerapkan konsep yang telah ia pelajari dengan memberikan latihan-latihan yang relevan dan realistik dari kehidupan sehari-hari.
23
David A. Sousa,Bagaimana Otak Belajar, (Jakarta: Indeks, 2012), h. 117. 24
Crawford,op. cit., h. 8. 25
4) Cooperating(bekerja sama)
Dalam kegiatan pembelajaran di kelas, seringkali persoalan atau kegiatan pemecahan masalah yang diberikan dianggap sulit oleh siswa, terutama jika diselesaikan secara individual. Berbagai kegiatan pemecahan masalah terutama yang berkaitan dengan situasi dunia nyata tidak jarang membuat siswa merasa frustasi karena mereka berpikir bahwa mereka tidak bisa menyelesaikannya. Dalam mengatasi masalah seperti ini, salah satu hal yang dapat dilakukan guru adalah dengan membiasakan kegiatan pembelajaran di kelas dalam bentuk kerjasama, yaitucooperating.
Cooperatingmencakupi suatu kelompok kecil siswa yang bekerja sebagai sebuah tim untuk menyelesaikan sebuah masalah, menyelesaikan suatu tugas, atau mengerjakan sesuatu untuk mencapai tujuan bersama lainnya.26 Cooperating yang diterapkan dalam pembelajaran tidak hanya membantu siswa dalam hal penguasaan materi pelajaran tapi juga menanamkan nilai bahwa keberhasilan akan lebih dapat dicapai melalui kerjasama.
5) Transferring(mentransfer)
Transferringadalah menggunakan pengetahuan ke dalam suatu konteks atau situasi baru yang belum tercakup dalam pembelajaran di kelas.27 Artinya siswa mampu menerapkan apa yang mereka pelajari dari satu situasi ke situasi yang baru. Dalam konteks matematika, transfer terjadi ketika siswa telah mempelajari suatu konsep matematika kemudian dapat menggunakannya untuk menyelesaikan permasalahan matematis dalam berbagai bidang lain.
Transferring dapat diwujudkan dengan mengondisikan siswa dengan berbagai pengalaman belajar.28Bentuk kegiatan yang terdapat pada strategi ini berupa kegiatan pemecahan masalah yang sifatnya baru bagi siswa. Masalah yang baru ini berarti bahwa masalah tersebut berbeda dari masalah yang biasanya diberikan pada siswa, yang menuntut siswa untuk dapat memroses informasi secara menyeluruh untuk mendapatkan makna dan mengaitkannya dengan pengetahuan yang telah didapatnya selama pembelajaran. Dalam hal
26
Erman Suherman, dkk.,op. cit, h. 218. 27
Crawford,op. cit., h. 14. 28
21
ini, guru dapat memberikan permasalahan yang memiliki konteks dan kombinasi konsep yang lebih kompleks, maupun yang memiliki kaitan dengan konsep pada mata pelajaran lain.
Berdasarkan uraian di atas, strategi pembelajaran REACT adalah strategi yang menitikberatkan pada keterlibatan siswa dalam berbagai aktivitas belajar mulai dari mengaitkan, mengalami, menerapkan, bekerja sama, dan mentrasfer pengetahuan.
b. TeknikScaffolding
Dalam strategi pembelajaran REACT, siswa didorong untuk terlibat aktif dalam berbagai kegiatan belajar, seperti mengaitkan, mengalami, menerapkan, bekerja sama hingga mentransfer pengetahuan. Namun, dalam prosesnya siswa diberikan bantuan yang terstruktur sehingga siswa dapat mengikuti pembelajaran dengan baik dan tujuan yang diharapkan dapat tercapai. Bantuan tersebut dikenal denganscaffolding.
1) Teori Vigotsky
Teori Vygotsky yang juga dikenal sebagai teori konstruktivisme sosial dirumuskan oleh seorang psikolog Rusia Lev Semenovich Vygotsky yang berkembang di dunia Barat pada awal tahun 1960-an. Teori Vygotsky menyatakan bahwa pengetahuan dan perkembangan kognitif terbentuk melalui internalisasi atau penguasaan proses sosial.29 Teori tersebut menunjukkan bahwa Vygotsky menekankan pentingnya pemanfaatan lingkungan yang diwujudkan dalam suatu interaksi sosial dalam pembelajaran.
Asumsi pokok dari teori Vygotsky adalah “what the child can do in cooperation today he can do alone tomorrow”.30Yang berarti apa yang dapat dilakukan oleh anak-anak dengan bekerja sama pada hari ini, ia akan dapat melakukannya sendiri di masa mendatang. Pernyataan ini mengandung makna bahwa fungsi mental anak dapat berkembang menuju tingkat yang lebih tinggi melalui interaksi sosial. Ketika seorang anak belum menguasai sesuatu,
29
Ibid, h. 19. 30
kemudian ia terlibat dalam suatu interaksi sosial yang dapat membantunya dalam membangun pemahaman, maka perkembangan kognitifnya akan meningkat sehingga kelak ia akan dapat melakukannya sendiri tanpa lagi membutuhkan bantuan orang lain.
Upaya mengimplementasikan teori Vigotsky dalam pembelajaran artinya kita perlu mengupayakan terciptanya suatu lingkungan yang kondusif bagi proses perkembangan kognitif anak. Lingkungan yang kaya akan berbagai fitur dan memfasilitasi terjadinya interaksi sosial yang positif dapat merangsang siswa untuk tertarik mempelajari dan membangun suatu konsep dan menginternalisasi pemahaman dalam dirinya.
Salah satu konsep dari teori Vygotsky adalah mengenaiZone Of Proximal Development atau ZPD. ZPD adalah daerah tingkat perkembangan sedikit di atas daerah perkembangan seseorang saat ini.31 The zone of proximal development is defined as the distance between the actual development level as determined by independent problem solving and the level of potential development as determined through problem solving under or in collaboration with more capable peers (Lipscomb,2004).32 Artinya, ZPD didefinisikan sebagai daerah antara tingkat perkembangan aktual yang ditandai dengan kemampuan pemecahan masalah secara mandiri dan tingkat perkembangan potensial yang ditandai melalui kemampuan pemecahan masalah di bawah bimbingan atau dengan berkolaborasi dengan orang dewasa atau teman sebaya yang lebih terampil. Sehingga dapat dikatakan bahwa batas bawah dari ZPD adalah tingkat pengetahuan yang dapat dicapai oleh anak secara mandiri, sedangkan batas atasnya adalah tingkat pengetahuan yang dapat dicapai siswa melalui bantuan orang lain yang lebih terampil.
Dalam pembelajaran guru perlu mengetahui ZPD siswa sehingga dapat menyesuaikan tugas-tugas dan instruksi yang diberikan. Mengetahui ZPD
31
Trianto, Model-Model Pembelajaran Inovatif Berorientasi Konstruktivistik, (Jakarta: Prestasi Pustaka Publisher, 2007), h. 27.
32
23
siswa dapat dilakukan dengan memberikan tugas-tugas dengan tingkat kesulitan yang beragam sehingga dapat diketahui tugas-tugas mana yang dapat diselesaikan siswa seorang diri dan tugas yang dapat diselesaikan siswa dengan bantuan dari guru maupun temannya. Konsep mengenai ZPD inilah yang kemudian mengarahkan pada istilahscaffolding.
2) TeknikScaffolding
Scaffolding dipercaya mampu membantu anak dalam mencapai ZPD. Teori scaffolding pertama kali diperkenalkan oleh Jerome Bruner, seorang psikolog kognitif pada akhir tahun 1950-an. Istilahscaffoldingsendiri pertama kali digunakan oleh Wood, dkk pada tahun 1976 yang mengartikannya sebagai dukungan pembelajar kepada peserta didik untuk membantunya menyelesaikan proses belajar yang tidak dapat diselesaikannya sendiri.33
Istilahscaffoldingberasal dari istilah dalam ilmu teknik sipil yaitu berupa bangunan kerangka sementara atau penyangga yang memudahkan pekerja membangun gedung.34 Kerangka sementara, artinya tidak digunakan terus menerus. Scaffolding digunakan pada masa-masa awal pembangunan, kemudian saat konstruksi bangunan sudah jadi scaffolding tidak lagi diperlukan.
Scaffoldingdalam implementasinya di bidang pendidikan memiliki makna yang sejalan dengan scaffolding dalam ilmu teknik sipil. Sejumlah pakar mendefinisikan scaffolding sebagai bimbingan yang diberikan pembelajar kepada peserta didik dalam proses pembelajaran dengan persoalan-persoalan terfokus dan interaksi yang positif.35 Ketika siswa menemui kesulitan untuk beranjak dari level kognitif yang dimilikinya saat ini, ia memerlukan bantuan (scaffolding) dari guru atau teman yang lebih terampil. Ketika ia sudah mampu membangun struktur pengetahuan yang lebih tinggi tersebut, maka ia sudah tidak lagi memerlukanscaffolding.Scaffoldingdiperlukan lagi ketika ia
33
Martinis Yamin, Paradigma Baru Pembelajaran, (Jakarta: Gaung Persada Press, 2011), h. 166.
34
Ibid, h. 165. 35
kembali menemui kesulitan untuk mencapai level kognitif yang lebih tinggi lagi.
Scaffolding dianalogikan sebagai jembatan yang dapat mengantarkan dan membantu siswa untuk membangun kemampuan kognitif baru berdasarkan pengetahuan terdahulu yang telah dimilikinya. Penafsiran terkini terhadap ide-ide Vygotsky adalah siswa seharusnya diberikan tugas-tugas kompleks, sulit, dan realistik dan kemudian diberikan bantuan secukupnya untuk menyelesaikan tugas-tugas itu.36 Jadi, guru perlu hadir untuk memberikan bantuan dan dukungan bagi siswa, terutama di masa-masa awal proses belajarnya sehingga ia dapat mencapai level kognitif yang lebih tinggi. Bantuan yang diberikan hanya berupa arahan atau media dalam menyelesaikan tugas namun tanggung jawab untuk menyelesaikan tugas tetap berada pada siswa. Seiring dengan kemampuan siswa yang semakin meningkat, tingkat bantuan yang diberikan semakin dikurangi hingga siswa akhirnya mencapai kemandirian dalam belajar.
Bentuk scaffolding yang dapat diberikan guru dalam pembelajaran beragam. Contoh-contoh aktivitas scaffolding dapat berupa apersepsi dan kontekstualisasi bahan ajar, memberikan pemandu grafis, memberikan isyarat atau petunjuk, memberikan contoh atau teladan, memberikan pertanyaan yang mengaktifkan pengetahuan siswa, panduan awal dalam menyelesaikan tugas, rangkuman, maupun memberikan refleksi di akhir pembelajaran.37
Diantara berbagai bentuk scaffolding yang dapat diberikan, dialog merupakan sebuah alat scaffolding yang penting dalam zona perkembangan proksimal. Menurut pandangan Vygotsky, anak-anak memiliki konsep-konsep yang kaya, tetapi tidak sistematis, tidak terorganisasi, dan spontan. Dalam sebuah dialog, konsep tersebut bertemu dengan konsep pembimbing yang lebih sistematis, logis, dan rasional. Hasilnya konsep anak menjadi lebih
36
Trianto,loc.cit. 37
25
sistematis, logis, dan rasional.38 Dialog yang dapat dilakukan seringkali berbentuk pertanyaan yang mengarahkan, diantaranya39:
Tabel 2.1
Tujuan dan PertanyaanScaffolding
Tujuan Pertanyaan
Memfokuskan Apakah yang diminta dari pertanyaan itu? Apakah yang harus kita cari? Informasi apa saja yang diberikan? Mengundang
partisipasi
Adakah yang mau menjawab pertanyaan ini? Siapa yang bisa meyebutkan …? Bisakah kamu menjelaskan jawaban ini di depan kelas?
Mengingatkan Adakah yang pernah menemukan masalah seperti ini? Adakah kemiripan antara masalah ini dengan …? Mengklarifikasi Apakah yang sedang kamu kerjakan? Mengapa kamu
berpikir demikian?
Mengevaluasi Apakah kamu yakin bahwa jawaban ini benar? Apakah ada jawaban lain?
Hogan dan Pressley menyatakan ada lima macam teknikscaffolding yang dapat diterapkan, yaitu40:
a) Memberikan teladan sesuai dengan perilaku yang diinginkan (modeling of desired behaviors) yaitu, guru mencontohkan perilaku ataupun cara berpikir yang diharapkan sesuai dengan situasi yang diberikan.
b) Memberikan penjelasan yang memadai dan relevan (offering explanation), yaitu memberikan penjelasan secara eksplisit mengenai apa yang dipelajari termasuk mengapa, kapan dan bagaimana ilmu itu digunakan.
c) Mengundang partisipasi siswa (inviting student participation) yaitu, siswa diberikan kesempatan untuk terlibat dalam proses belajar yang sedang
38
John Santrock,Psikologi Pendidikan, (Jakarta: Salemba Humanika, 2009), h. 64. 39
Paul Lau Ngee Kiong dan Hwa Tee Yong, Scaffolding as a Teaching Strategy To Enhance Mathematics Learning in The Classroom, 2001, h. 10-11, dari www.ipbl.edu.my pada 12 September 2014 pukul 11.52.
40
berlangsung. Setelah guru memberikan ilustrasi dari ide dan langkah yang dibutuhkan untuk menyelesaikan tugas, siswa berpartisipasi dengan melanjutkan langkah penyelesaian sesuai dengan apa yang mereka ketahui.
d) Melakukan verifikasi dan klarifikasi terhadap pemahaman siswa (verifying and clarifying student understanding) yaitu, guru memberikan umpan balik terhadap hasil pekerjaan siswa, dengan melakukan verifikasi jika pemahaman siswa benar dan dapat diterima, jika tidak maka guru mengklarifikasi pemahaman siswa.
e) Mengundang para siswa untuk memberikan petunjuk kunci (inviting students to contribute clues) yaitu, mengajak siswa untuk berpartisipasi dengan mengungkapkan gagasan, petunjuk dan pendapatnya dalam menyelesaikan tugas.
c. Tahapan Strategi Pembelajaran REACT Dengan Teknik Scaffolding
Terhadap Kemampuan Koneksi Matematik
27
Tabel 2.2
Tahapan Strategi Pembelajaran REACT dengan Teknik Scaffolding
Terhadap Kemampuan Koneksi Matematik Kegiatan Pembelajaran Komponen
REACT
Kemampuan Koneksi - Guru memulai pelajaran dengan menggali
pengetahuan prasyarat siswa dan memberikan ilustrasi dan pertanyaan yang dekat dengan kehidupan siswa yang berkaitan dengan materi yang akan dipelajari agar siswa melihat kaitannya dengan kehidupan ataupun dengan pengetahuan yang telah ia miliki. Siswa berpartisipasi dengan menjawab pertanyaan sesuai dengan pemahamannya (inviting student participation)
- Siswa dibentuk ke dalam kelompok yang beranggotakan 4 siswa dan diberikan LKS. - Guru mencontohkan langkah-langkah yang
perlu dilakukan siswa dalam menyelesaikan LKS (modeling of desired behaviors).
- Siswa berdiskusi dengan kelompoknya untuk mengerjakan LKS sehingga siswa dapat membangun pengetahuan sendiri. - Guru mengontrol jalannya diskusi
kelompok serta menawarkan bantuan melalui pertanyaan arahan atau penjelasan jika diperlukan (offering explanation). - Guru memberikan latihan yang realistik
dan relevan untuk mengukur pemahaman siswa.
Relating
Cooperating
Experiencing
Applying
- Antar topik matematik - Mata pelajaran lain - Kehidupan sehari-hari
Kegiatan Pembelajaran Komponen REACT
Kemampuan Koneksi - Siswa diberikan kesempatan untuk
mempresentasikan hasil diskusinya. Siswa lain menanggapi dan turut menyampaikan gagasannya (inviting student participation) - Guru memberikan umpan balik dengan
memverifikasi pemahaman siswa yang sudah tepat dan mengklarifikasi pemahaman yang kurang tepat (verifying and clarifying student understanding) - Guru memberikan masalah yang berbeda
dari segi konteks maupun kombinasi konsep dari masalah yang biasa diberikan. Masalah tersebut dapat berupa aplikasi konsep dalam disiplin ilmu lain maupun masalah matematika dengan kompleksitas yang lebih tinggi.
- Guru membimbing siswa untuk membuat kesimpulan dan melakukan refleksi atas apa yang telah dipelajari. Siswa diajak untuk menyatakan gagasan dan hal-hal yang telah ia pahami (inviting student to contribute clues).
Transferring
matematik
- Antar topik matematik - Mata
pelajaran lain - Kehidupan
sehari-hari
Pembelajaran menggunakan strategi REACT dengan teknik Scaffolding memiliki beberapa kelebihan, di antaranya :
29
2) Siswa difasilitasi untuk melihat dan menggunakan hubungan yang ada antara materi yang dipelajarinya dengan materi yang telah ia pelajari sebelumnya dan dengan kehidupan sehari-hari sehingga siswa dapat melihat matematika secara menyeluruh dan motivasi belajar siswa meningkat.
3) Siswa dibimbing melalui pertanyaan-pertanyaan yang mengarahkan sehingga dapat melatih kemampuan siswa dalam berpikir kritis, logis dan rasional. 4) Siswa dibiasakan untuk bekerja sama dalam kelompok belajar sehingga siswa
dapat terlatih untuk memiliki rasa tanggung jawab dan menghargai orang lain.
3. Pembelajaran Konvensional
Pembelajaran konvensional adalah pembelajaran yang sering diterapkan oleh guru dalam kegiatan pembelajaran hingga saat ini. Pembelajaran konvensional yang terdapat pada sekolah tempat dilaksanakan penelitian merupakan pembelajaran yang berpusat pada guru dan memposisikan siswa sebagai penerima informasi tanpa terlibat secara langsung dalam berbagai aktivitas belajar. Siswa umumnya diberikan informasi yang “sudah jadi” tanpa difasilitasi untuk membangun pengetahuannya sendiri. Dampak yang timbul adalah pembelajaran mempunyai kesan lebih mengutamakan hasil daripada proses yang dijalani. Akhirnya siswa lebih mengandalkan hapalan dibandingkan membangun pemahaman. Metode dan strategi yang sering digunakan dalam pembelajaran konvensional adalah metode ceramah dan strategi ekspositori.
Pembelajaran konvensional yang digunakan dalam penelitian ini adalah pembelajaran dengan strategi ekspositori. Strategi ekspositori adalah strategi pembelajaran yang menekankan pada proses penyampaian materi secara verbal dari seorang guru kepada sekelompok siswa dengan maksud agar siswa dapat menguasai materi pelajaran secara optimal.41 Jadi dalam strategi ekspositori, materi pelajaran diberikan secara langsung kepada siswa tanpa menuntut dan mengkondisikan siswa untuk terlibat dalam proses menemukan pengetahuan.
41
Strategi ekspositori memiliki beberapa karakteristik, diantaranya adalah42: a. Strategi pembelajaran ekspositori dilakukan dengan cara menyampaikan
materi pelajaran secara lisan
b. Materi pelajaran yang disampaikan adalah materi pelajaran yang sudah jadi sehingga tidak menuntut siswa untuk berpikir ulang
c. Tujuan utama pembelajaran adalah penguasaan pembelajaran itu sendiri Adapun langkah-langkah dalam strategi ekspositori adalah43:
a. Persiapan (preparation)
Tahap ini berkaitan dengan mempersiapkan siswa untuk menerima pelajaran. Kegiatan dalam tahap ini seperti menyampaikan tujuan pembelajaran dan melakukan apersepsi.
b. Penyajian (presentation)
Dalam tahap ini guru menyampaikan materi pelajaran kepada siswa. Guru mengusahakan agar materi pelajaran dapat dengan mudah ditangkap dan dipahami oleh siswa.
c. Korelasi (correlation)
Pada tahap ini guru menghubungkan materi pelajaran dengan pengalaman siswa. Hal ini dilakukan untuk memberikan makna terhadap materi pelajaran. d. Menyimpulkan (generalization)
Tahap ini adalah tahapan mengambil dan memahami inti sari dari materi pelajaran yang telah disampaikan.
e. Mengaplikasikan (application)
Tahap ini adalah tahapan unjuk kemampuan siswa setelah menyimak penjelasan dari guru dengan mengerjakan latihan yang diberikan.
B. Hasil Penelitian yang Relevan
1. Penelitian Sugiman (2008) dalam jurnalnya yang berjudul “Koneksi Matematik dalam Pembelajaran Matematika di Sekolah Menengah Pertama”. Hasil pen