TUGAS AKHIR
STUDI PENYELESAIAN PROBLEMA MIXED INTEGER LINIER
PROGRAMMING DENGAN MENGGUNAKAN
METODE BRANCH AND CUT
OLEH :
RISTA RIDA SINURAT 040803023
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
MEDAN
ABSTRAK
DAFTAR ISI
Halaman judul Persetujuan Pernyataan Abstrak Abstract Daftar Isi Daftar Tabel Daftar Gambar Bab 1 Pendahuluan
1.1 Latar Belakang 1
1.2 Perumusan Masalah 2
1.3 Tujuan Penelitian 3
1.4 Manfaat Penelitian 3
1.5 Tinjauan Pustaka 3
1.6 Metodologi Penelitian 4
Bab II Landasan Teori
2.1 Program Linier 6
2.1.1 Karakteristik-karakteristik dalam Program Linier 6
2.2.2 Asumsi dalam Program Linier 6
2.2 Klasifikasi Integer Programming 7
2.3 Metode Penyelesaian Masalah Mixed Integer linier Programming 7
2.3.1 Metode Cutting Plane 11
2.3.2 Metode Enumerasi 20
2.3.2.1 Metode Branch-And-Bound 20
2.4 Himpunan Konveks, Kombinasi Konveks 54
2.5 Fungsi konveks dan Fungsi konkaf 55
Bab III Pembahasan
3.1 Bentuk Umum Masalah Mixed Integer Linier Programming 57
3.2 Algoritma Branch-And-Cut 58
3.3 Contoh Persoalan 59
Bab IV Kesimpulan dan Saran
4.1 Kesimpulan 73
BAB 1
PENDAHULUAN
1.1Latar Belakang
Banyak masalah dalam bidang ekonomi, industri, teknik dan militer yang dapat dinyatakan sebagai model matematika. Masalah-masalah ini antara lain dapat diformulasikan sebagai model program linier.
Pada masalah maksimum atau minimum, setiap model variabel dapat bernilai real. Dalam beberapa kondisi sering mendekati atau mempunyai penyelesaian pecahan. Sebagai contoh, ketebalan bidang 2,66 mm pada struktur bangunan, waktu kerja 3,34 jam pada suatu proyek dan penggunaan 1,78 kg pupuk utuk menambah kesuburan tanah. Walaupun demikian, ada juga masalah dimana nilai pecahan dari model variabel tidak berarti secara fisik. Sebagai contoh sebuah pabrik yang ingin memproduksi pakaian yang ingin memperbesar produksinya. Pabrik ini tidak dapat membeli mesin pembuat kain delapan setengah unit, walaupun anggaran belanja yang dimiliki oleh pabrik tersebut memungkinkan,atau tidak mungkin menggunakan 1,6 ketel pada pembangkit tenaga listrik, jumlah tenaga kerja 1,9 orang pada suatu proyek dan 2,76 mesin bubut pada suatu toko.
Walaupun demikian dalam banyak kasus optimisasi, sangat sulit membulatkan penyelesaian tanpa melangggar beberapa dari kendala. Sering terjadi jika memprediksi variabel yang tepat, perlu mengganti nilai dari beberapa variabel untuk memenuhi semua kendala. Akibatnya jika membulatkan penyelesaian bisa saja memberikan suatu nilai fungsi objektif yang sangat jauh dari nilai optimal awal. Semua kesulitan-kesulitan ini dapat dihindari jika masalah optimisasi dimodelkan dan diselesaikan sebagai masalah program linier.
dinyatakan sebagai masalah mixed integer programming. Mixed Integer Linier
Programming (MILP) sering juga disebut mixed integer programming.
Relaksasi linier programming adalah suatu program linier yang dihasilkan dari program integer linier programming dengan menghilangkan persyaratan bilangan bulat untuk variabel keputusannya.
Banyak metode yang bisa digunakan untuk menyelesaikan masalah Mixed
Integer Linier Programming (MILP) yang masing-masing mempunyai kelebihan dan
kelemahan. Memperhatikan hal ini maka penulis mencoba mempelajari metode Branch-And-Cut dalam menyelesaikan masalah Mixed Integer Linier Programming (MILP).
Perhatikan model Mixed integer linier programming (MILP), yaitu :
Optimisasikan :
∑
∑
=
= +
= p
k k k n
j j
jx d y
c Z
1 1
Dengan kendala :
1.2 Perumusan Masalah
Pokok permasalahan dalam karya tulis ini adalah bagaimana mencari atau menyelesaikan masalah Mixed Integer Linier Programming (MILP) dengan menggunakan metode Branch And Cut.
(
)
p k
y
n j
eger dan
x
m i
b y
g x
a
k j
i p
k k ik n
j j ij
, , 3 , 2 , 1 0
, , 3 , 2 , 1
int ,
0
, , 3 , 2 , 1
, ,
1 1
= ≥
= ≥
=
= ≥ ≤ +
∑
1.3Tujuan Penelitian
Tujuan dari penulisan ini adalah mencari penyelesaian (solusi optimal) dari masalah
Mixed integer linier programming dengan menggunakan metode Branch-And-Cut.
1.4 Manfaat Penelitian
Adapun manfaat dari penelitian ini adalah untuk memperkaya literature dan menambah pengetahuan bagi penulis dan pembaca khususnya dalam menyelesaikan masalah Mixed integer linier programming.
1.5Tinjauan Pustaka
Karena penelitian ini merupakan studi literature maka tinjauan pustaka adalah titik tolak yang utama dalam tulisan ini. Penulis melakukan tinjauan pustaka dari :
Rao S. S. dalam bukunya menjelaskan bahwa pada problema optimisasi dengan adanya kendala linier dan terdapat beberapa variabel yang dibatasi bernilai integer, masalah optimisasi ini dinyatakan sebagai masalah mixed integer
programming.
Nasendi B. D. dalam bukunya menjelaskan bahwa program integer (PI) terbagi dua yaitu program integer asli (PIA) dan program integer tercampur (PIT). PIA adalah suatu program linier yang semua peubahnya adalah integer, sedangkan PIT adalah suatu program linier yang sebahagian peubahnya integer dan sebahagian lagi adalah peubah kontinu atau peubah divisible (nonintegre). Dalam bahasa Inggris program integer asli biasa dikenal sebagai Pure integer programming, sedangkan program integer tercampur sebagai Mixed integer linier programming.
Fitri Maya Puspita dalam jurnalnya menjelaskan bahwa masalah Mixed
Integer Linier Programming muncul ketika beberapa variabel dalam masalah linier
seperti : jumlah manusia, mesin, botol, kotak dan lain-lain. Terdapat dua pendekatan untuk menyelesaikan Mixed Integer Linier Programming (MILP) yaitu metode exact dan metode heuristic. Teknik exact meliputi metode Branch-And-Cut dan metode Branch-And-Bound.
1.6Metodologi Penelitian
Tulisan ini disusun atas kerangka pemikiran yang langkah-langkahnya adalah sebagai berikut :
1. Diberikan pengertian dan definisi dari integer linier programming. 2. Diberikan pengertian dan definisi dari mixed integer linier programming. 3. Diberikan pengertian dan definisi dasar dari metode Cutting Plane beserta
contohnya.
4. Diberikan pengertian dan definisi dasar dari metode Branch-And-Bound beserta contohnya.
5. Diberikan pengertian dan definisi dasar dari metode Branch-And-Cut dan memodelkan sebuah permasalahan sebagai aplikasinya.
ABSTRAK
BAB 1
PENDAHULUAN
1.1Latar Belakang
Banyak masalah dalam bidang ekonomi, industri, teknik dan militer yang dapat dinyatakan sebagai model matematika. Masalah-masalah ini antara lain dapat diformulasikan sebagai model program linier.
Pada masalah maksimum atau minimum, setiap model variabel dapat bernilai real. Dalam beberapa kondisi sering mendekati atau mempunyai penyelesaian pecahan. Sebagai contoh, ketebalan bidang 2,66 mm pada struktur bangunan, waktu kerja 3,34 jam pada suatu proyek dan penggunaan 1,78 kg pupuk utuk menambah kesuburan tanah. Walaupun demikian, ada juga masalah dimana nilai pecahan dari model variabel tidak berarti secara fisik. Sebagai contoh sebuah pabrik yang ingin memproduksi pakaian yang ingin memperbesar produksinya. Pabrik ini tidak dapat membeli mesin pembuat kain delapan setengah unit, walaupun anggaran belanja yang dimiliki oleh pabrik tersebut memungkinkan,atau tidak mungkin menggunakan 1,6 ketel pada pembangkit tenaga listrik, jumlah tenaga kerja 1,9 orang pada suatu proyek dan 2,76 mesin bubut pada suatu toko.
Walaupun demikian dalam banyak kasus optimisasi, sangat sulit membulatkan penyelesaian tanpa melangggar beberapa dari kendala. Sering terjadi jika memprediksi variabel yang tepat, perlu mengganti nilai dari beberapa variabel untuk memenuhi semua kendala. Akibatnya jika membulatkan penyelesaian bisa saja memberikan suatu nilai fungsi objektif yang sangat jauh dari nilai optimal awal. Semua kesulitan-kesulitan ini dapat dihindari jika masalah optimisasi dimodelkan dan diselesaikan sebagai masalah program linier.
dinyatakan sebagai masalah mixed integer programming. Mixed Integer Linier
Programming (MILP) sering juga disebut mixed integer programming.
Relaksasi linier programming adalah suatu program linier yang dihasilkan dari program integer linier programming dengan menghilangkan persyaratan bilangan bulat untuk variabel keputusannya.
Banyak metode yang bisa digunakan untuk menyelesaikan masalah Mixed
Integer Linier Programming (MILP) yang masing-masing mempunyai kelebihan dan
kelemahan. Memperhatikan hal ini maka penulis mencoba mempelajari metode Branch-And-Cut dalam menyelesaikan masalah Mixed Integer Linier Programming (MILP).
Perhatikan model Mixed integer linier programming (MILP), yaitu :
Optimisasikan :
∑
∑
=
= +
= p
k k k n
j j
jx d y
c Z
1 1
Dengan kendala :
1.2 Perumusan Masalah
Pokok permasalahan dalam karya tulis ini adalah bagaimana mencari atau menyelesaikan masalah Mixed Integer Linier Programming (MILP) dengan menggunakan metode Branch And Cut.
(
)
p k
y
n j
eger dan
x
m i
b y
g x
a
k j
i p
k k ik n
j j ij
, , 3 , 2 , 1 0
, , 3 , 2 , 1
int ,
0
, , 3 , 2 , 1
, ,
1 1
= ≥
= ≥
=
= ≥ ≤ +
∑
1.3Tujuan Penelitian
Tujuan dari penulisan ini adalah mencari penyelesaian (solusi optimal) dari masalah
Mixed integer linier programming dengan menggunakan metode Branch-And-Cut.
1.4 Manfaat Penelitian
Adapun manfaat dari penelitian ini adalah untuk memperkaya literature dan menambah pengetahuan bagi penulis dan pembaca khususnya dalam menyelesaikan masalah Mixed integer linier programming.
1.5Tinjauan Pustaka
Karena penelitian ini merupakan studi literature maka tinjauan pustaka adalah titik tolak yang utama dalam tulisan ini. Penulis melakukan tinjauan pustaka dari :
Rao S. S. dalam bukunya menjelaskan bahwa pada problema optimisasi dengan adanya kendala linier dan terdapat beberapa variabel yang dibatasi bernilai integer, masalah optimisasi ini dinyatakan sebagai masalah mixed integer
programming.
Nasendi B. D. dalam bukunya menjelaskan bahwa program integer (PI) terbagi dua yaitu program integer asli (PIA) dan program integer tercampur (PIT). PIA adalah suatu program linier yang semua peubahnya adalah integer, sedangkan PIT adalah suatu program linier yang sebahagian peubahnya integer dan sebahagian lagi adalah peubah kontinu atau peubah divisible (nonintegre). Dalam bahasa Inggris program integer asli biasa dikenal sebagai Pure integer programming, sedangkan program integer tercampur sebagai Mixed integer linier programming.
Fitri Maya Puspita dalam jurnalnya menjelaskan bahwa masalah Mixed
Integer Linier Programming muncul ketika beberapa variabel dalam masalah linier
seperti : jumlah manusia, mesin, botol, kotak dan lain-lain. Terdapat dua pendekatan untuk menyelesaikan Mixed Integer Linier Programming (MILP) yaitu metode exact dan metode heuristic. Teknik exact meliputi metode Branch-And-Cut dan metode Branch-And-Bound.
1.6Metodologi Penelitian
Tulisan ini disusun atas kerangka pemikiran yang langkah-langkahnya adalah sebagai berikut :
1. Diberikan pengertian dan definisi dari integer linier programming. 2. Diberikan pengertian dan definisi dari mixed integer linier programming. 3. Diberikan pengertian dan definisi dasar dari metode Cutting Plane beserta
contohnya.
4. Diberikan pengertian dan definisi dasar dari metode Branch-And-Bound beserta contohnya.
5. Diberikan pengertian dan definisi dasar dari metode Branch-And-Cut dan memodelkan sebuah permasalahan sebagai aplikasinya.
BAB 2
LANDASAN TEORI
Integer programming merupakan bagian dari program matematika (mathematical
programming). Adapun permasalahan program matematika secara umum dapat
dinyatakan sebagai :
Optimisasikan Z
( )
x , x∈S ⊆ Rn dengan R adalah himpunan semua vektor real n nkomponen dan z suatu fungsi real yang didefenisikan dalam S. himpunan S dinamakan himpunan kendala (constraint) dan z disebut fungsi objektif (objective
function).
Permasalahan pada program matematika bertujuan untuk mencari solusi optimal. Untuk mencari solusi optimal tersebut, harus diketahui apa yang dimaksud dengan solusi layak (feasible solution). Setiap x∈S pada persamaan di atas disebut sebagai solusi layak, sedangkan untuk x0∈S yang memenuhi
( )
<( )
0 <∞x z x
z ,
S x∈
∀ dinyatakan sebagai solusi optimal (optimal solution) dari persamaan di atas yang memaksimumkan Z
( )
x . Masalah program matematika dengan S ⊆ Zn ⊆ Rn, dan Z himpunan semua vektor bilangan bulat n komponen, disebut masalah integer nprogramming.
2.1 Program Linier
2.1.1 Karakteristik-karakteristik dalam program linier
Dalam membangun model dari formulasi akan digunakan karakteristik-karakteristik yang biasa digunakan dalam persoalan program linier yaitu:
a. Variabel keputusan
Variabel keputusan adalah variabel yang menguraikan secara lengkap keputusan-keputusan yang akan dibuat.
b. Fungsi tujuan
Fungsi tujuan merupakan fungsi dari variabel keputusan yang akan dimaksimumkan (pendapatan atau keuntungan) atau diminimumkan (biaya atau ongkos)
c. Pembatas
Pembatas merupakan kendala yang dihadapi sehingga kita tidak bisa menentukan harga-harga variabel keputusan secara sembarang.
d. Pembatas tanda
Pembatas tanda adalah yang menjelaskan apakah variabel keputusannya diasumsikan hanya berharga negatif atau variabel keputusanya boleh berharga positif.
2.1.2 Asumsi dalam Model Program linier
Dalam menggunakan model program linier, diperlukan beberapa asumsi sebagai berikut:
a. Asumsi kesebandingan (proposionality)
• Kontribusi suatu variabel keputusan terhadap ruas kiri dari setiap pembatas juga sebanding dengan nilai variabel keputusan itu.
b. Asumsi penambahan (additivity)
• Kontribusi setiap variabel keputusan terhadap fungsi tujuan tidak bergantung pada nilai dari variabel keputusan yang lain.
• Kontribusi suatu variabel keputusan terhadap ruas kiri dari setip pembatas bersifat tidak bergantung pada nilai dari variabel keputusan yang lain. c. Asumsi pembagian (divisibility)
Dalam persoalan program linier, variabel keputusan boleh diasumsikan berupa bilangan pecahan.
d. Asumsi kepastian (certainty)
Setiap parameter, yaitu koefisien fungsi tujuan, ruas kanan, dan koefisien teknologi, diasumsikan dapat diketahui secara pasti.
2.2 Klasifikasi Integer Programming
Berdasarkan variabel keputusan yang diperoleh, masalah integer programming dapat dibedakan menjadi dua, yakni:
1. Pure Integer Programming
Pure integer programming adalah masalah integer programming dimana semua variabel keputusannya terbatas hanya untuk bilangan bulat.
Bentuk umum dari pure integer programming adalah: Optimisasikan :
∑
=
= n j
j jx
c Z
Dengan kendala
(
)
n j m i eger x b x c j i n j j j , , 3 , 2 , 1 , , 3 , 2 , 1 int , 0 , , 1 = = ≥ = ≥ ≤∑
=Dengan aij, bi, dan cj adalah konstanta.
2. Mixed Integer Programming
Mixed integer programming adalah masalah integer programming dengan beberapa variabel keputusannya dibatasi sebagai bilangan bulat, dan sementara yang lain tidak. Bentuk umum dari mixed integer programming adalah :
Optimasasikan :
∑
∑
= = + = p k k k n j j
jx d y
c Z 1 1 Dengan kendala
(
)
p k y n j eger dan x m i b y g x a k j i p k k ik n j j ij , , 3 , 2 , 1 0 , , 3 , 2 , 1 int , 0 , , 3 , 2 , 1 , , 1 1 = ≥ = ≥ = = ≥ ≤ +∑
∑
= =Masalah integer programming dapat juga dibedakan dari fungsi yang ada pada fungsi obyektif dan kendala-kendala pada masalah tersebut. Pada masalah integer programming ini fungsi obyektif dan kendala-kendalanya berupa persamaan atau pertidaksamaan linier maka masalah ini disebut integer linier programming. Sebaliknya bila fungsi tidak linier, masalah integer programming ini disebut sebagai masalah nonlinier programming.
( )
xZ = - maksimum (-Z(x)). Dengan menghapus syarat bilangan bulat, masalah mixed integer linier programming akan berubah menjadi masalah program linier biasa. Mudah untuk dimengerti bahwa program linier merupakan perluasan dari mixed integer linier programming.
Untuk lebih jelasnya perhatikan masalah P dan 1 P berikut: 2
1
P : maksimumkan Z
( )
x , x∈S1 2P : maksimumkan Z
( )
x , x∈S2Bila S2 ⊆S1 maka P pembatas 2 P . 1
Bila x0 solusi optimal P dan 1 x* solusi optimal P , maka 2 z
( ) ( )
x0 ≥ z x* . Jika Sx0∈ maka x0 juga solusi optimal P , karena bila 2
( )
( )
* 00
x z x z S
x ∈ → ≤ maka
( ) ( )
0 * x z xz = .
2.3Metode Penyelesaian Masalah Mixed Integer Linier Programming
Pemograman linier bilangan bulat campuran pada intinya berkaitan dengan program linier dimana beberapa atau semua variabel memiliki nilai-nilai integer (bulat) atau diskrit.
Kesulitan perhitungan dengan metode penyelesaian masalah mixed integer linir programming yang tersedia telah mengarahkan penganalisa untuk mencari cara-cara lain untuk memecahkan masalah yang bersangkutan. Salah satu pendektan yang dilakukan adalah memecahkan persoalan tersebut selayaknya program linier dengan mengabaikan syarat integernya. Kemudian hasil pemecahan optimal linier tersebut dibulatkan kenilai integer yang terdekat dan yang juga layak. Tetapi tidak ada jaminan dalam kasus ini bahwa pemecahan yang dibulatkan tersebut akan memenuhi kendala-kendala.
dapat mentolerir ketidaklayakan yang berasal dari pembulatan. Tetapi terdapat batasan persamaan tertentu dalam masalah mixed integer dimana parameter-parameternya pasti. Metode simpleks yang digunakan dalam penyelesaian program linier, didasarkan pada pengenalan bahwa pemecahan optimal terjadi dititik ekstrim ruang pemecahan. Hasil yang penting ini awalnya mengurangi usaha pencarian pemecahan optimal dari sejumlah pemecahan yang tidak terbatas menjadi jumlah yang terbatas.
Hingga saat ini belum ada suatu metode umum, seperti metode simpleks dalam masalah program linier, yang dapat dipergunakan untuk menyelesaikan semua masalah mixed integer linier programming dengan hasil yang memuaskan. Setiap masalah mixed integer linier programming mempunyai metode penyelesaian tersendiri untuk mendapatkan hasil yang baik. Walaupun demikian semua metode ini berdasarkan pada salah satu pendekatan di bawah ini :
1. Metode Cutting-Plane, 2. Metode Enumerasi, 3. Metode Dekomposisi, 4. Algoritma Group Theory.
Penelitian untuk mendapatkan suatu metode yang paling memuaskan masih dilakukan sampai sekarang.
2.3.1 Metode Cutting Plane
Dasar pemikiran dari metode ini adalah membentuk kendala baru sebagai bidang pemotongan daerah layak yang tidak mengandung solusi bilangan bulat. Dalam metode ini dibangun syarat pemotogan dengan menggunakan iterasi dari metode simpleks didapatkan solusi optimal yang bulat.
Maksimum
∑
∑
= = + = p k k k n j jjx d y
c Z 1 1 Dengan kendala
(
)
p k y n j eger dan x m i b y g x a k j i p k k ik n j j ij , , 3 , 2 , 1 0 , , 3 , 2 , 1 int , 0 , , 3 , 2 , 1 , , 1 1 = ≥ = ≥ = = ≥ ≤ +∑
∑
= =Didefenisikan, x harus bernilai bulat. Dengan syarat bahwa setiap variabel *j solusi memenuhi batas-batas pada persamaan kendala. Jika setiap variabel xj sudah merupakan bilangan bulat, maka itu sudah merupakan solusi optimal. Yang ditunjukan dengan.
[ ]
[
+δ]
=[ ]
+δ∑
= a xj bn j j j 1 2.1 Dimana
[ ]
aj dan[ ]
b dinyatakan sebagai bilangan bulat, kemudian diperoleh :[ ]
a xj[ ]
bn
j
j ≤
∑
=1 2.2Dan
[ ]
a xj S[ ]
bn
j
j + =
∑
=1 2.3Dimana S adalah variabel slack. Jika terjadi pengurangan pada persamaan 2..3 oleh persamaan 2.1 maka akan diperoleh :
( )
−δ + =−δ∑
n=j
j S
x 1
2.4
Dalam menyelesaikan masalah MILP, jika salah satu variabel yang dibatasi bernilai integer tetapi belum bernilai integer maka periksa baris dalam tabel simpleks akhir yang menunjukan nilai variabel yang belum bulat. Misalkan bahwa x adalah B
variabel tersebut yang ditunjukan sebagai berikut:
∑
=+ m
m m
B B x b
Dimana x bukan variabel dasar. Kita lanjutkan kebentuk persamaan 2.4, maka m
didapat:
( )
−δ + =−δ∑
xm Sm m
Dimana
[ ]
[ ] [ ]
bB
m
m m m
− =
− =
φ δ φ δ
Nilai δ adalah bilangan yang kongruen dengan bilangan real φ. Dengan
[ ]
φ adalah bilangan bulat yang terdekat dengan φContoh :
Tabel 1
Berdasarkan metode iterasi simpleks yang digunakan ada dua jenis metode Cutting-Plane, yaitu metode Dual Cutting-Plane yang dikembangkan oleh Ralph Gomory dan Primal Cutting-Plane yang dikembangkan oleh Glover danYoung. Metode Dual Cutting-Plane menggunakan metode dual simpleks untuk menyelesaikan masalah program liniernya.
Metode Dual Cutting-Plane oleh Ralph Gomory dibedakan lagi menjadi : 1. Metode Dual Fractional Integer Programming.
2. Metode Dual Fractional Mixed Integer Programming. 3. Metode Dual All Integer Programming.
δ φ
[ ]
φ 2/3 -4/3 -2 1/2 5/2 20 -5 -5
0 1 1
Contoh :
Maksimumkan Z =4x1−2x2 +7x3 −x4 2.5
Dengan kendala 3 , 2 , 1 4 , 3 , 2 , 1 0 3 2 2 0 5 6 1 10 5 4 3 1 2 1 3 2 1 3 1 = = ≥ ≤ − + − ≤ − ≤ − + ≤ + j untuk bulat x j untuk x x x x x x x x x x x j j
Masalah tersebut ditransformasikan menjadi :
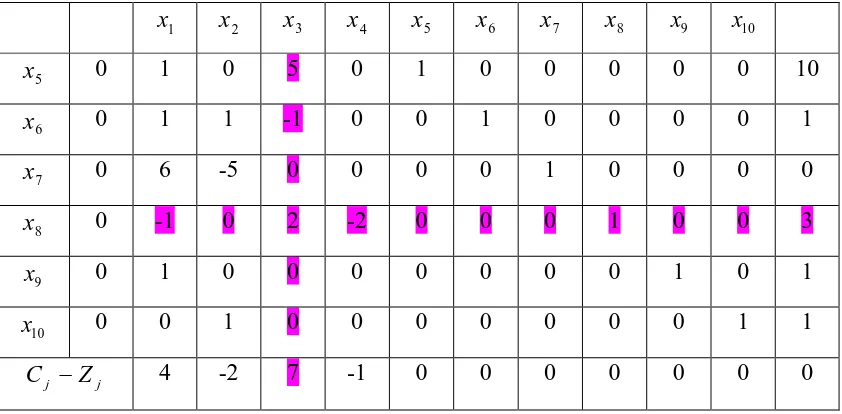
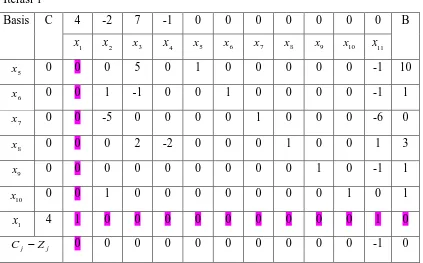
Tabel 1. Tabel simpleks 1 Iterasi 0
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x3 x 4 x 5 x 6 x 7 x 8
5
x 0 1 0 5 0 1 0 0 0 10
6
x 0 1 1 -1 0 0 1 0 0 1
7
x 0 6 -5 0 0 0 0 1 0 0
8
x 0 -1 0 2 -2 0 0 0 1 3
j j Z
C − 4 -2 7 -1 0 0 0 0 0
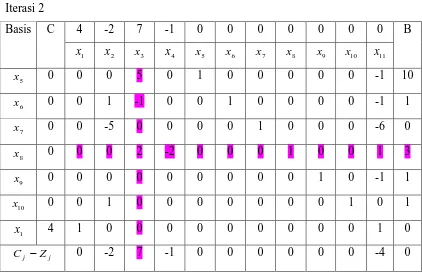
Tabel 2. Tabel simpleks 2 Iterasi 1
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8
5
x 0
2
7 0 0 5 1 0 0
2 5
−
2 5
6
x 0
2
1 1 0 -1 0 1 0
2 1
2 5
1
x 0 6 -5 0 0 0 0 1 0 0
3
x 7
2 1
− 0 1 -1 0 0 0
2 7
2 3
j j Z
C −
2
15 -2 0 6 0 0 0
2 7
−
2 21
Tabel 3. Tabel simpleks 3 Iterasi 2
basis
C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x 3 x4 x 5 x 6 x 7 x 8
5
x 0 0
12
35 0 5 1 0
12 7
−
2 5
−
2 5
6
x 0 0
12
17 0 -1 0 1
12 1 −
2 1
2 5
1
x 4 1
12 10
− 0 0 0 0
12 2
− 0 0
3
x 7 0
12 5
− 1 -1 0 0
12 1
2 1
2 3
j j Z
C − 0
2
9 0 6 0 0
4 5
−
2 7
−
2 21
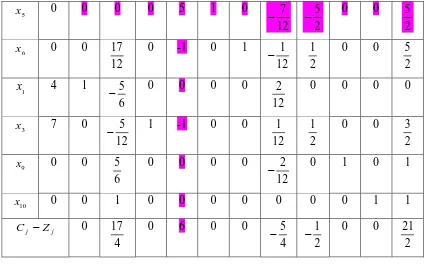
Tabel 4. Tabel simpleks 4 Iterasi 3
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8
4
x -1 0
12
7 0 1
5
1 0
60 7
−
2 1
−
6
x 0 0 2 0 0
5
1 1
5 1
− 0 3
1
x 4 1
12 10
− 0 0 0 0
12
2 0 0
3
x 7 0
12
11 1 0
5
1 0
20
11 0 2
j j Z
C − 0
4
3 0 0
5 6 − 0 20 11 − 2 1 − 2 27
Tabel 5. Tabel simpleks 5 Iterasi 4
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8
2
x -2 0 1 0
7 12 35 12 0 5 1 − 7 6 − 7 6 6
x 0 0 0 0
7 24 − 35 17 − 1 5 1 7 12 7 9 1
x 4 1 0 0
7 10
7
2 0 0
7 5 − 7 5 3
x 7 0 0 1
7 2
−
7
1 0 0
7 1 7 13 j j Z
C − 0 0 0
7 9 − 35 16 − 0 12 5 − 7 1 7 99
Tabel 6. Tabel simpleks 6 Iterasi 5
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8
2
x -2 0 1 0 0
10 1 2 1 10 1 − 0 2 3 8
x 0 0 0 0 -2
1
x 4 1 0 0 0
12 1 12 5 12 1 0 4 5 3
x 7 0 0 1 0
60 11 12 1 − 60 1 − 0 4 7 j j Z
C − 0 0 0 -1
12 17 − 12 1 − 12 5 − 0 4 57
Solusi optimal yang diperoleh yaitu :
4 1 14 0 , 4 7 , 2 3 , 4 5 4 3 2
1 = x = x = x = dengan Z =
x
Karena solusi belum bernilai integer , maka perlu ditambahkan bidang pemotongan : 4 5 12 1 12 5 12 1 7 6 5
1+ x + x + x =
x 4 1 12 1 12 5 12 1 4 1 1 12 1 0 12 5 0 12 1 0 7 6 5 6 5 1 − ≤ − − − + = + + + + + + x x x x x x Diperoleh 4 1 12 1 12 5 12 1 9 7 6
5− − + =−
− x x x x
Tabel 7. Tabel simpleks 7 Iterasi 6
basis C 4 -2 7 -1 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9
2
x -2 0 1 0 0
10 1 2 1 10 1
− 0 0
2 3
8
x 0 0 0 0 -2
60 17 − 12 7 60
7 1 0
4 3
1
x 4 1 0 0 0
12 1
12 5
12
1 0 0
3
x 7 0 0 1 0
60 11
12 1
−
60 1
− 0 0
4 7
9
x 0 0 0 0 0
12 1
−
12 5
−
12 1
− 0 1
4 1
−
j j Z
C − 0 0 0 -1
12 17
−
12 1 −
12 5
− 0 0
4 57
Tabel 8. Tabel simpleks 8 Iterasi 7
basis C 4 -2 7 -1 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9
2
x -2 0 1 0 0 0 0
5 1
− 0
5 6
5 6
8
x 0 0 0 0 -2
6
1 0 0 1
5 7
5 2
1
x 4 1 0 0 0 0 0 0 0 1 1
3
x 7 0 0 1 0
5
1 0 0 0
5 1
−
5 9
6
x 0 0 0 0 0
5
1 1
5
1 0
5 12
−
5 3
j j Z
C − 0 0 0 -1
5 7
− 0
5 2
− 0
5 1
−
5 71
Solusi optimal yang diperoleh yaitu :
5 1 14 0
, 5 9 ,
5 6 ,
1 2 3 4
1 = x = x = x = dengan Z =
x
Karena nilai x dan 2 x belum merupakan bilangan bulat maka kita tambahkan lagi 3
pemotongan ditinjau dari baris pertama :
5 6 5 6 5 1
9 7
2− x + x =
5 1 5 1 5 4 5 1 1 5 1 1 5 4 1 9 7 9 7 2 − ≤ − − + = + + +− + x x x x x Diperoleh : 5 1 5 1 5 4 10 9
7 − + =−
− x x x
Tabel 9. Tabel simpleks 9 Iterasi 8
basis C 4 -2 7 -1 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10
2
x -2 0 1 0 0 0 0
5 1 − 0 5 6 0 5 6 8
x 0 0 0 0 -2
6
1 0 0 1
5
7 0
5 2
1
x 4 1 0 0 0 0 0 0 0 1 0 1
3
x 7 0 0 1 0
5
1 0 0 0
5 1 − 0 5 9 6
x 0 0 0 0 0
5 1 1 5 1 0 5 12 − 0 5 3 10
x 0 0 0 0 0 0 0
5 4 − 0 5 1 − 1 5 1 − j j Z
C − 0 0 0 -1
5 7 − 0 5 2 − 0 5 1 − 0 5 71
Tabel 10 . Tabel simpleks 10 Iterasi 9
basis C 4 -2 7 -1 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10
2
x -2 0 1 0 0 0 0 0 0
8
x 0 0 0 0 -2
6
1 0 0 1
5
7 0
5 2
1
x 4 1 0 0 0 0 0 0 0 1 0 1
3
x 7 0 0 1 0
5
1 0 0 0
5 1 − 0 5 9 6
x 0 0 0 0 0
5
1 1 0 0
5 12 − 0 5 3 7
x 0 0 0 0 0 0 0 1 0
4 1 4 5 − 4 1 j j Z
C − 0 0 0 -1
5 7 − 0 5 2 − 0 5 1 − 2 1 − 10 141
Solusi optimal yang diperoleh yaitu :
10 1 14 0 , 5 9 , 4 5 ,
1 2 3 4
1 = x = x = x = dengan Z =
x
Karena nilai x dan 2 x belum merupakan bilangan bulat maka kita tambahkan lagi 3
pemotongan ditinjau dari baris keempat :
5 9 5 1 5 1 9 7
3 + x − x =
x 5 4 5 4 5 1 5 4 1 5 4 1 5 1 0 9 7 9 7 3 − ≤ − − + = +− + + + x x x x x Diperoleh : 5 4 5 4 5 1 11 9
7 − + =−
− x x x
Tabel 11. Tabel simpleks 11 Iterasi 10
basis C 4 -2 7 -1 0 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11
2
x -2 0 1 0 0 0 0 0 0
8
x 0 0 0 0 -2
6
1 0 0 1
5
7 0 0
5 2
1
x 4 1 0 0 0 0 0 0 0 1 0 0 1
3
x 7 0 0 1 0
5
1 0 0 0
5 1
− 0 0
5 9
6
x 0 0 0 0 0
5
1 1 0 0
5 12
− 0 0
5 3
7
x 0 0 0 0 0 0 0 1 0
4 1
4 5 − 0
4 1
11
x 0 0 0 0 0
5 1
− 0 0 0
5 4
− 0 1
5 4 −
j j Z
C − 0 0 0 -1
5 7 − 0
5 2 − 0
5 1 −
2 1 − 0
10 141
Tabel 12. Tabel simpleks 12 Iterasi 11
basis C 4 -2 7 -1 0 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11
4
x -1 0 1 0 1 0 0 0
2 1
− 0 0
12 5
2 1
9
x 0 0 0 0 0 0 0 0 0 1 0 0 1
10
x 0 1 0 0 0 0 0
5 4
− 0 0 1 0 0
3
x 7 0 0 1 0 0 0 0 0 0 0 0 2
6
x 0 0 0 0 0 0 1 0 0 0 0 0 3
7
x 0 0 0 0 0 0 0
5 1
− 0 0 0 0 0
5
x 0 0 0 0 0 0 0 0 0 0 0 -5
j j Z
C − 0 0 0 0 0 0
5 2
−
2 1
− 0 0
12 88
−
2 27
Karena x ,1 x dan 2 x sudah bernilai integer maka telah diperoleh solusi optimal 3
yang sudah merupakan bilangan bulat yaitu :
2 1 13 2
1 ,
2 ,
0 ,
0 2 3 4
1 = x = x = x = dengan Z =
x
Maka dapat disimpulkan pemotongan yang dilakukan adalah
2 1 13 7x3 −x4 ≥
2.3.2 Metode Enumerasi
Dengan anggapan bahwa setiap persoalan Mixed Integer Linier Programming yang terbatas akan mempunyai solusi layak yang terhingga (finite), maka wajar bila digunakan prosedur enumerasi untuk mendapatkan solusi bilangan bulat untuk persoalan tersebut. Tetapi akibatnya jumlah solusi yang terhingga ini biasanya sangat banyak sehingga sukar untuk menentukan solusi yang terbaik.
Sebagai contoh, bila terdapat 10 variabel yang dibatasi bernilai integer dan masing-masing mempunyai 10 harga yang layak (fesible solution), maka solusi layak dapat mencapai 1010 walaupun persoalan ini dibantu oleh komputer, waktu yang dibutuhkan relatif lama. Untuk itu digunakan cara enumerasi yang hanya memeriksa sebahagian dari solusi layak tersebut.
Metode yang lain adalah enumerasi implisit, dimana metode ini digunakan bila masalah yang dihadapi hanya memerlukan keputusan ya atau tidak. Dengan perkataan lain semua variabel bilangan bulat adalah binary (0 atau 1). Metode enumerasi implisit pertama kali dikembangkan oleh Egon Balas, kemudian banyak lagi algoritma enumerasi implist yang lain.
2.3.2.1 Metode Branch-And-Bound
Masalah Mixed Integer Linier Programming adalah masalah integer programming dimana beberapa variabel dibatasi harus bernilai bulat (tetapi tidak harus 0 atau1) dan sisanya berupa peubah kontinu biasa. Struktur dari algoritma ini pertama kali dikembangkan oleh R. J. Dakin, berdasarkan pada algoritma Branch-and-Bound pendahulu yang dikembangkan oleh A. H. Land dan A. G. Doig.
Struktur algoritma ini agak mirip dengan algoritma dasar pemogramam bilangan bulat biner. Dengan menyelesaikan PL-relaksasinya akan memberikan lagi suatu dasar untuk kedua langkah pembatasan dan penghentian.
Diberikan masalah Mixed Integer Linier Programming sebagai berikut:
Maksimum
∑
∑
=
= +
= p
k k k n
j j
jx d y
c Z
1 1
Dengan kendala
(
)
p k
y
n j
eger dan
x
m i
b y
g x
a
k j
i p
k k ik n
j j ij
, , 3 , 2 , 1 0
, , 3 , 2 , 1
int ,
0
, , 3 , 2 , 1
, ,
1 1
= ≥
= ≥
=
= ≥ ≤ +
∑
∑
= =terbatas hanya untuk 0-1 maka kita sebutkan sebagai Integer Linier programming Biner. Jika beberapa variabel dibatasi bernilai integer maka kita sebutkan sebagai Mixed Integer Linier Programming.
Konsep dasar dari metode Branch-And-Bound adalah pengamatan terhadap tiap-tiap nilai xj, diberikan [xj]≤xj ≤[xj]+1 dimana [xj] adalah bilangan bulat terdekat yang lebih kecil dari xj. Sebagai contoh, misalkan dicari nilai xj yang bulat dan dengan metode simpleks diperoleh nilai x*j =4,3. Kemudian dicari solusi bilangan bulat, sehingga dapat dibuat pencabangan masalah menjadi dua masalah terpisah dan himpunan yang lengkap, yang memenuhi xj ≤5,0 dan 4,0≤ xj.
Dilakukan pengamatan, dibuat masalah awal menjadi dua masalah yang baru. Inilah yang disebut dengan Branch (pencabangan). Perlu diingat bahwa solusi awal menjadi batas atas (upper bound) pada solusi optimal. Penambahan pertidaksamaan sebagai pencabangan masalah akan mengakibatkan berkurangnya nilai dari solusi optimal awal. Lebih lanjut proses ini akan membentuk masalah baru dalam bentuk pohon untuk mencari alternatif-altenatif yang mungkin sebagai solusi optimal yang merupakan bilangan bulat.
Sebagai salah satu hasil pencabangan variabel yang belum bulat pada setiap cabang, satu dari dua kejadian akan berhasil. Yang pertama, solusi yang mungkin diperoleh tidak memenuhi syarat bilangan bulat dari variabel yang dicabangkan, dan memperoleh nilai fungsi objektif yang kurang sesuai dibandingkan dengan pencabangan lain yang semua solusinya sudah bilangan bulat, dalam kasus ini pencabangan dilanjutkan. Yang kedua, mungkin diperoleh solusi lain, sudah memenuhi syarat bilangan bulat, dalam kasus ini ditinggalkan pencabangan.
optimal akan diperoleh apabila semua proses pencabangan sudah terlaksana. Apabila tidak ditemukan solusi layak maka disimpulkan bahwa pencabangan tersebut berada di luar daerah layak.
Terdapat dua tahap yang dipakai dalam algoritma pencabangan dan pembatasan, yaitu:
1. Pencabangan, yaitu mempartisi masalah tersebut menjadi sub-submasalah dengan cara menambahkan kendala yang merupakan syarat perlu untuk mencari solusi bilangan bulat fesibel tanpa mengubah himpunan solusi bilangan bulat semula.
2. Pembatasan, yaitu nilai fungsi obyektif dari suatu submasalah yangn mempunyai solusi bilangan bulat dipakai sebagai batas nilai fungsi obyektif dari submasalah lainnya. Jadi, jika operasi pencabangan dan pembatasan dilakukan secara teliti, maka banyak submasalah yang mengandung satu atau lebih titik bilangan bulat fesibel dapat dibuang secara otomatis.
Algoritma Metode Branch-And-Bound
Langkah awal : Tetapkan Z* =−∞. gunakan langkah pembatasan, langkah penghentian, dan uji keoptimalan seperti yang diberikan dibawah ini pada masalah keseluruhan. Jika masalah tersebut tidak terhenti, maka golongkan masalah ini sebagai suatu “submasalah” sisa untuk melakukan iterasi penuh pertama dibawah ini.
Langkah-langkah untuk setiap iterasi:
1. Pencabangan: diantara submasalah sisa (yang belum terhenti), pilih satu submasalah yang dibuat paling akhir. (jika lebih dari satu pilihan submasalah dengan batas lebih besar) diantara peubah-peubah yang dibatasi bulat yang mempunyai nilai bukan bilangan bulat pada penyelesaian optimal untuk program linier-relaksasi suatu submasalah, pilih satu peubah pertama dalam urutan asli menjadi peubah pencabangan. Misalkan xj adalah peubah ini, dan
*
j
ini untuk membuat dua submasalah baru dengan menambahkan kendala
] [ j
j x
x ≤ dan xj ≤[x*j]+1
2. Pembatasan: untuk setiap submasalah baru, cari batas submasalahnya dengan menggunakan metode simpleks (atau metode simpleks dual bila diperlukan pengoptimisasian kembali) pada program linier relaksasi dan dengan menggunakan nilai Z untuk penyelesaian optimal yang dihasilkan.
3. Penghentian: untuk setiap submasalah baru, gunakan ketiga uji penghentian yang diberikan di bawah ini, dan buang submasalah yang dihentikan dengan suatu uji.
Uji 1 :Batasnya ≤Z* dengan Z adalah nilai Z untuk “incumbent” *
saat ini.
Uji 2 :Program linier relaksasinya tidak mempunyai penyelesaian layak
Uji 3 :Penyelesaian optimal untuk program linier relaksasinya mempunyai nilai bilangan bulat untuk peubah-peubah yang dibatasi bulat. Jika penyelesaian ini lebih baik dari pada ‘incumbent’nya, maka penyelesaian ini menjadi ‘incumbet’baru dan uji 1 digunakan kembali untuk semua submasalah yang belum terselesaikan dengan Z baru yang *
lebih besar.
Contoh
Maksimumkan Z =4x1−2x2 +7x3 −x4
Dengan kendala 3 , 2 , 1 4 , 3 , 2 , 1 0 3 2 2 0 5 6 1 10 5 4 3 1 2 1 3 2 1 3 1 = = ≥ ≤ − + − ≤ − ≤ − + ≤ + j untuk bulat x j untuk x x x x x x x x x x x j j
Masalah tersebut ditransformasikan menjadi :
Perhatikan bahwa banyaknya variabel yang dibatasi bulat adalah sebanyak 3 buah variabel sehingga x adalah satu-satunya peubah kontinu. 4
Langkah awal: setelah menetapkan Z* =−∞. kita bentuk program linier relaksasi dari masalah ini dengan menghilangkan gugus kendala xj adalah bilangan bulat untuk j=1,2,3. Dengan menggunakan metode simpleks program linier relaksasi diperoleh :`
Tabel 13. Tabel simpleks 13 Iterasi 0
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x3 x 4 x 5 x 6 x 7 x 8
5
x 0 1 0 5 0 1 0 0 0 10
6
x 0 1 1 -1 0 0 1 0 0 1
7
x 0 6 -5 0 0 0 0 1 0 0
8
x 0 -1 0 2 -2 0 0 0 1 3
j j Z
C − 4 -2 7 -1 0 0 0 0 0
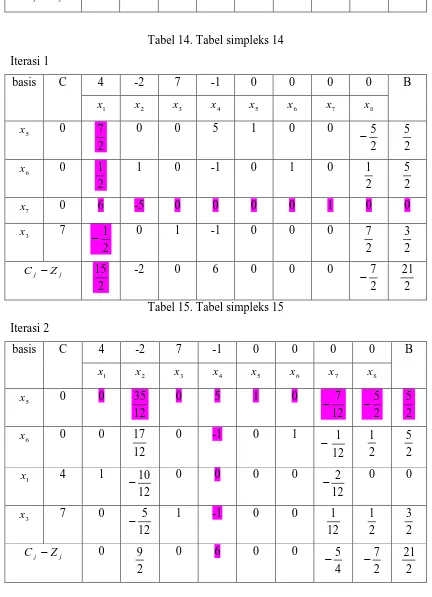
Tabel 14. Tabel simpleks 14 Iterasi 1
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8
5
x 0
2
7 0 0 5 1 0 0
2 5
−
2 5
6
x 0
2
1 1 0 -1 0 1 0
2 1
2 5
7
x 0 6 -5 0 0 0 0 1 0 0
3
x 7
2 1
− 0 1 -1 0 0 0
2 7
2 3
j j Z
C −
2
15 -2 0 6 0 0 0
2 7 −
[image:35.595.103.535.125.722.2]2 21
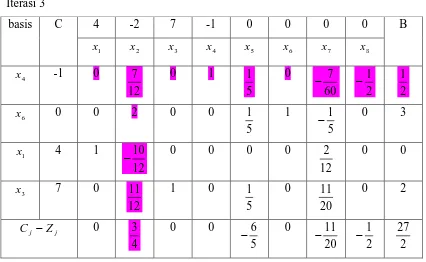
Tabel 15. Tabel simpleks 15 Iterasi 2
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x 3 x4 x 5 x 6 x 7 x 8
5
x 0 0
12
35 0 5 1 0
12 7
−
2 5
−
2 5
6
x 0 0
12
17 0 -1 0 1
12 1 −
2 1
2 5
1
x 4 1
12 10
− 0 0 0 0
12 2
− 0 0
3
x 7 0
12 5
− 1 -1 0 0
12 1
2 1
2 3
j j Z
C − 0
2
9 0 6 0 0
4 5
−
2 7
−
2 21
Iterasi 3
basis C 4 -2 7 -1 0 0 0 0 B
1
x x2 x 3 x 4 x 5 x 6 x 7 x 8
4
x -1 0
12
7 0 1
5 1 0 60 7 − 2 1 − 2 1 6
x 0 0 2 0 0
5
1 1
5 1
− 0 3
1
x 4 1
12 10
− 0 0 0 0
12
2 0 0
3
x 7 0
12
11 1 0
5
1 0
20
11 0 2
j j Z
C − 0
4
3 0 0
[image:36.595.107.533.89.351.2]5 6 − 0 20 11 − 2 1 − 2 27
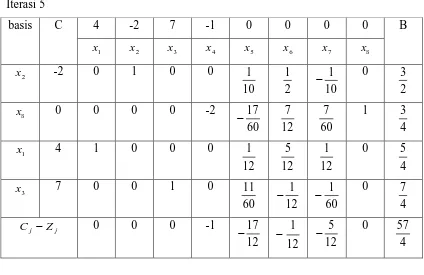
Tabel 17. Tabel simpleks 17 Iterasi 4
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8
2
x -2 0 1 0
7 12 35 12 0 5 1 − 7 6 − 7 6 6
x 0 0 0 0
7 24 − 35 17 − 1 5 1 7 12 7 9 1
x 4 1 0 0
7 10
7
2 0 0
7 5 − 7 5 3
x 7 0 0 1
7 2
−
7
1 0 0
7 1 7 13 j j Z
C − 0 0 0
Tabel 18.Tabel simpleks 18 Iterasi 5
basis C 4 -2 7 -1 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8
2
x -2 0 1 0 0
10 1
2 1
10 1
− 0
2 3
8
x 0 0 0 0 -2
60 17 −
12 7
60
7 1
4 3
1
x 4 1 0 0 0
12 1
12 5
12
1 0
4 5
3
x 7 0 0 1 0
60 11
12 1 −
60 1
− 0
4 7
j j Z
C − 0 0 0 -1
12 17 −
12 1 −
12 5
− 0
4 57
PL-relaksasi dari masalah ini adalah :
4 1 14 0
, 4 7 ,
2 3 ,
4 5
4 3
2
1 = x = x = x = dengan Z =
x
Karena PL-relaksasi ini mempunyai penyelesaian layak dan penyelesaian optimal ini mempunyai nilai yang bukan bilangan bulat untuk vaiabel-variabel yang dibatasi bulat, maka pada masalah akan dilakukan pencabangan (branch) pada salah satu variabel yang belum bulat, misalkan x dicabangkan, sehingga masalah keseluruhan 1
tidak dihentikan sehingga algoritma tersebut dilanjutkan.
Iterasi 1 :
Dalam penyelesaian optimal untuk PL-relaksasi, variabel yang dibatasi integer yang pertama mempunyai nilai yang bukan bilangan bulat adalah
4 5
1 =
x , sehingga x 1
Submasalah 1:
Maksimumkan Z =4x1−2x2 +7x3 −x4 . . . . 2.6 Dengan kendala
3 , 2 , 1
4 , 3 , 2 , 1 0
1 3 2 2
0 5
6
1 10 5
1 4 3 1
2 1
3 2 1
3 1
= = ≥
≤ ≤ − + −
≤ −
≤ −
+
≤ +
j untuk bulat
x
j untuk x
x x x x
x x
x x x
x x
j j
Dengan menghilangkan syarat bilangan bulat dan menyelesaikan PL-relaksasi dari submasalah 1 diperoleh:
Tabel 19. Tabel simpleks 19 Iterasi 0
basis C 4 -2 7 -1 0 0 0 0 0 B
1
x x 2 x3 x 4 x 5 x 6 x 7 x 8 x 9
5
x 0 1 0 5 0 1 0 0 0 0 10
6
x 0 1 1 -1 0 0 1 0 0 0 1
7
x 0 6 -5 0 0 0 0 1 0 0 0
8
x 0 -1 0 2 -2 0 0 0 1 0 3
9
x 0 1 0 0 0 0 0 0 0 0 1
j j Z
C − 4 -2 7 -1 0 0 0 0 0 0
Tabel 20. Tabel simpleks 20 Iterasi 1
basis C 4 -2 7 -1 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9
5
x 0
2
7 0 0 5 1 0 0
2 5
− 0
6
x 0
2
1 1 0 -1 0 1 0
2
1 0
2 5
7
x 0 6 -5 0 0 0 0 1 0 0 0
3
x 7
2 1
− 0 1 -1 0 0 0
2
1 0
2 3
9
x 0 1 0 0 0 0 0 0 0 1 1
j j Z
C −
2
15 -2 0 6 0 0 0
2 7
− 0
2 21
Tabel 21. Tabel simpleks 21 Iterasi 2
basis C 4 -2 7 -1 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9
5
x 0 0
12
35 0 5 1 0
12 7 −
2 5
− 0
2 5
6
x 0 0
12
17 0 -1 0 1
12 1 −
2
1 0
2 5
1
x 4 1
12 10
− 0 0 0 0
12
2 0 0 0
3
x 7 0
12 5
− 1 -1 0 0
12 1
2
1 0
2 3
9
x 0 0
12
10 0 0 0 0
12 1
− 0 1 1
j j Z
C − 0
4
17 0 6 0 0
4 5 −
2 7
− 0
2 21
Tabel 22. Tabel simpleks 22 Iterasi 3
basis C 4 -2 7 -1 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9
4
x -1 0
12
7 0 1
5
1 0
60 7 −
2 1
− 0
6
x 0 0 2 0 0
5
1 1
5 1
− 0 0 3
1
x 4 1
12 10
− 0 0 0 0
6
1 0 0 0
3
x 7 0
12
2 1 0
5
1 0
30 1
− 0 0 2
9
x 0 0
12
10 0 0 0 0
6 1
− 0 1 1
j j Z
C − 0
4
3 0 0
[image:40.595.109.536.347.634.2]5 6 − 0 20 11 5 1 − 0 2 27
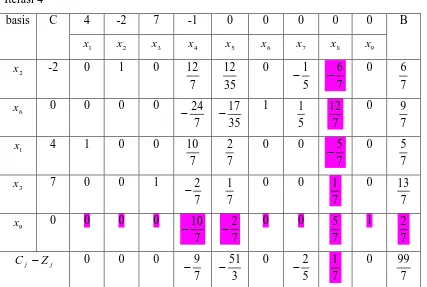
Tabel 23. Tabel simpleks 23 Iterasi 4
basis C 4 -2 7 -1 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9
2
x -2 0 1 0
7 12 35 12 0 5 1 − 7 6 − 0 7 6 6
x 0 0 0 0
7 24 − 35 17 − 1 5 1 7 12 0 7 9 1
x 4 1 0 0
7 10
7
2 0 0
7 5 − 0 7 5 3
x 7 0 0 1
7 2
−
7
1 0 0
7
1 0
7 13
9
x 0 0 0 0
7 10
−
7 2
− 0 0
7 5 1 7 2 j j Z
C − 0 0 0
7 9 − 3 51 − 0 5 2 − 7 1 0 7 99
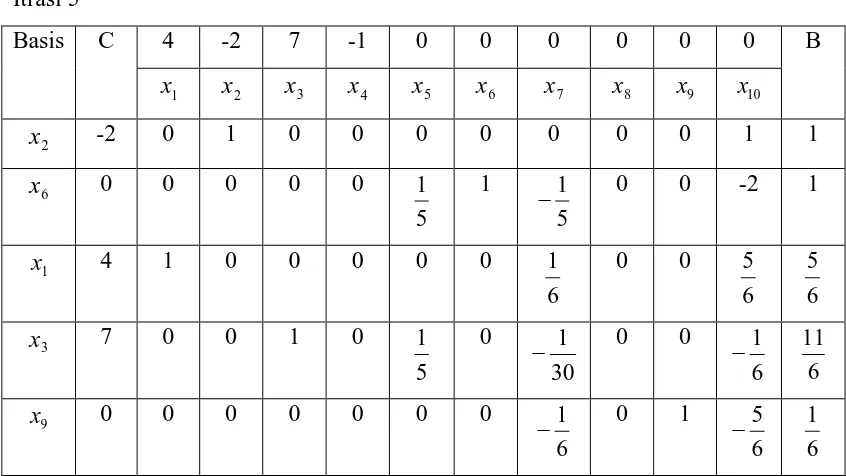
Tabel 24. Tabel simpleks 24 Iterasi 5
basis C 4 -2 7 -1 0 0 0 0 0 B
1
2
x -2 0 1 0 0 0 0
5 1 − 0 5 6 5 6 6
x 0 0 0 0 0
5 1 1 5 1 0 5 12 5 3 1
x 4 1 0 0 0 0 0 0 0 1 1
3
x 7 0 0 1 0
5
1 0 0 0
5 1 − 5 9 8
x 0 0 0 0 -2
5 2
− 0 0 1
5 7 5 2 j j Z
C − 0 0 0 -1
5 7 − 0 5 2 − 0 5 1 − 5 71
Penyelesaian optimum untuk PL-relaksasi submasalah 1 :
5 1 14 0 , 5 9 , 5 6 ,
1 2 3 4
1 = x = x = x = dengan Z =
x
Batas untuk submasalah 1 adalah
5 1 14 ≤ Z Submasalah 2
Maksimumkan Z =4x1−2x2 +7x3 −x4 . . . 2. 7
Dengan kendala 3 , 2 , 1 4 , 3 , 2 , 1 0 2 3 2 2 0 5 6 1 10 5 1 4 3 1 2 1 3 2 1 3 1 = = ≥ ≥ ≤ − + − ≤ − ≤ − + ≤ + j untuk bulat x j untuk x x x x x x x x x x x x j j
Hasil untuk submasalah 2 ini berarti bahwa submasalah 2 ini dihentikan dengan uji 2. Sehingga, seperti pada masalah awal, submasalah 1 dilanjutkan setelah diuji dengan semua uji penghentian.
Iterasi 2:
Hanya dengan satu submasalah sisa yaitu yang berkaitan dengan simpul x1 ≤1, maka pencabangan berikutnya dilakukan dari simpul ini. Dengan mencari penyelesaian optimal dari PL-relaksasi yang diberikan di bawah ini, simpul ini menampakan bahwa variabel pencabangannya adalah x karena 2
5 6
2 =
x adalah variabel yang dibatasi bulat pertama yang mempuyai nilai noninteger. Dengan menambahkan satu dari kendala-kendala, yaitu x2 ≤1 atau x2 ≥2, maka akan menghasilkan dua submasalah baru, yaitu :
Submasalah 3
Maksimumkan Z =4x1−2x2 +7x3 −x4 . . . 2.8
Dengan kendala
3 , 2 , 1
4 , 3 , 2 , 1 0
1 1 3 2 2
0 5
6
1 10 5
2 1 4 3 1
2 1
3 2 1
3 1
= = ≥
≤ ≤ ≤ − + −
≤ −
≤ −
+
≤ +
j untuk bulat
x
j untuk x
x x x x x
x x
x x x
x x
j j
Dengan menyelesaikan PL-relaksasi submasalah 3 tersebut memberikan hasil :
Tabel 25. Tabel simpleks 25 Iterasi 0
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10
5
x 0 1 0 5 0 1 0 0 0 0 0 10
6
x 0 1 1 -1 0 0 1 0 0 0 0 1
7
x 0 6 -5 0 0 0 0 1 0 0 0 0
8
x 0 -1 0 2 -2 0 0 0 1 0 0 3
9
x 0 1 0 0 0 0 0 0 0 1 0 1
10
x 0 0 1 0 0 0 0 0 0 0 1 1
j j Z
[image:43.595.110.531.84.291.2]C − 4 -2 7 -1 0 0 0 0 0 0 0
Tabel 26. Tabel simpleks 26 Iterasi 1
Basis C 4 -2 7 -1 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10
5
x 0
2
7 0 0 5 1 0 0
2 5
− 0 0
2 5
6
x 0
2
1 1 0 -1 0 1 0
2
1 0 0
2 5
7
x 0 6 -5 0 0 0 0 1 0 0 0 0
3
x 7
2 1
− 0 1 -1 0 0 0
2
1 0 0
2 3
9
x 0 1 0 0 0 0 0 0 0 1 0 1
10
x 0 0 1 0 0 0 0 0 0 0 1 1
j j Z
C −
2
15 -2 0 6 0 0 0
2 7
− 0 0
[image:43.595.108.533.336.647.2]2 21
Tabel 27. Tabel simpleks 27 Iterasi 2
Basis C 4 -2 7 -1 0 0 0 0 0 0 B
1
5
x 0 0 0 0 5 1 0
12 7
−
2 5
− 0 0
2 5
6
x 0 0
12
17 0 -1 0 1
12 1
−
2
1 0 0
2 5
1
x 4 1
6 5
− 0 0 0 0
12
2 0 0 0 0
3
x 7 0
12 5
− 1 -1 0 0
12 1
2
1 0 0
2 3
9
x 0 0
6
5 0 0 0 0
12 2
− 0 1 0 1
10
x 0 0 1 0 0 0 0 0 0 0 1 1
j j Z
C − 0
4
17 0 6 0 0
4 5
−
2 1
− 0 0
[image:44.595.106.532.84.349.2]2 21
Tabel 28. Tabel simpleks 28 Iterasi 3
Basis C 4 -2 7 -1 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10
4
x -1 0
12
7 0 1
5 1 0 60 7 − 2 1
− 0 0
2 1
6
x 0 0 2 0 0
5
1 1
5 1
− 0 0 0 3
1
x 4 1
6 5
− 0 0 0 0
12
2 0 0 0 0
3
x 7 0
12
2 1 0
5
1 0
30 1
− 0 0 0 2
9
x 0 0
6
5 0 0 0 0
12 2
− 0 1 0 1
10
x 0 0 1 0 0 0 0 0 0 0 1 1
j j Z
C − 0
4
3 0 0
5 6 − 0 20 11 − 2 1
− 0 0
Tabel 29. Tabel simpleks 29 Iterasi 4
Basis C 4 -2 7 -1 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10
2
x -2 0 1 0
7 12 35 12 0 5 1 − 7 6
− 0 0
7 6
6
x 0 1 0 0
7 24 − 35 17 − 1 5 1 7
12 0 0
7 9
1
x 4 0 0 0
7 10
7
2 0 0
7 5
− 0 0
7 5
3
x 7 0 0 1
7 2 −
7
1 0 0
7
1 0 0
7 13
9
x 0 0 0 0
7 10 −
7 2
− 0 0
7
5 1 0
7 2
10
x 0 0 0 0
7 12 − 35 12 − 0 5 1 7
6 0 1
7 1
j j Z
C − 0 0 0
7 9 − 35 51 − 0 5 2 − 7
1 0 0
7 99
Tabel 30. Tabel simpleks 30 Itrasi 5
Basis C 4 -2 7 -1 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10
2
x -2 0 1 0 0 0 0 0 0 0 1 1
6
x 0 0 0 0 0
5
1 1
5 1
− 0 0 -2 1
1
x 4 1 0 0 0 0 0
6
1 0 0
6 5
6 5
3
x 7 0 0 1 0
5
1 0
30 1
− 0 0
6 1 − 6 11 9
x 0 0 0 0 0 0 0
6 1
− 0 1
6 5 −
[image:45.595.107.530.514.752.2]8
x 0 0 0 0 -2
5 2
− 0
30
7 1 0
6 7 6 1 j j Z
C − 0 0 0 -1
5 7
− 0
30 13
− 0 0
6 1
−
6 85
Penyelesaian optimal untuk PL-relaksasi submasalah 3 adalah :
6 1 14 0 , 6 11 , 1 , 6 5 4 3 2
1 = x = x = x = dengan Z =
x
Sehinggga batas untuk submasalah 3 adalah
6 1 14 ≤ Z Submasalah 4:
Maksimumkan Z =4x1−2x2 +7x3 −x4 . . . 2.9 Dengankendala 3 , 2 , 1 4 , 3 , 2 , 1 0 2 1 3 2 2 0 5 6 1 10 5 2 1 4 3 1 2 1 3 2 1 3 1 = = ≥ ≥ ≤ ≤ − + − ≤ − ≤ − + ≤ + j untuk bulat x j untuk x x x x x x x x x x x x x j j
Dengan menyelesaikan submasalah 4 diperoleh :
Tabel 31 Tabel simpleks 31 Iterasi 0
Basis C 4 -2 7 -1 0 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11
5
x 0 1 0 5 0 1 0 0 0 0 0 0 10
6
x 0 1 1 -1 0 0 1 0 0 0 0 0 1
7
x 0 6 -5 0 0 0 0 1 0 0 0 0 0
8
9
x 0 1 0 0 0 0 0 0 0 1 0 0 1
10
x 0 0 1 0 0 0 0 0 0 0 1 -1 2
j j Z
C − 0 1 0 0 0 0 0 0 0 0 -1 2
Tabel 32 Tabel simpleks 32 Iterasi 1
Basis C 4 -2 7 -1 0 0 0 0 0 0 0 B
1
x x 2 x3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11
5
x 0 1 0 5 0 1 0 0 0 0 0 0 10
2
x -2 1 1 -1 0 0 1 0 0 0 0 0 1
7
x 0 11 0 -5 0 0 5 1 0 0 0 0 5
8
x 0 -1 0 2 -2 0 0 0 1 0 0 0 3
9
x 0 1 0 0 0 0 0 0 0 1 0 0 1
10
x 0 -1 0 1 0 0 -1 0 0 0 1 -1 1
j j Z
C − -1 0 1 1 0 -1 0 0 0 0 -1 1
Tabel 33. Tabel simpleks 33 Iterasi 2
Basis C 4 -2 7 -1 0 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11
5
x 0 6 0 0 0 1 5 0 0 0 -5 5 5
2
x -2 0 1 0 0 0 0 0 0 0 1 -1 2
7
x 0 6 0 0 0 0 0 1 0 0 5 -5 10
8
x 0 1 0 0 -2 0 2 0 1 0 -2 2 1
9
x 0 1 0 0 0 0 0 0 0 1 0 0 1
3
x 7 -1 0 1 0 0 -1 0 0 0 1 -1 1
j j Z
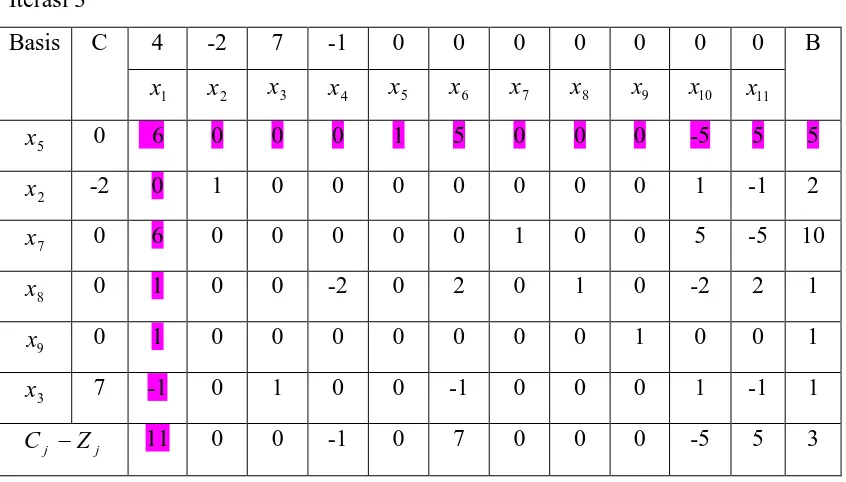
Tabel 34. Tabel simpleks 34 Iterasi 3
Basis C 4 -2 7 -1 0 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11
5
x 0 6 0 0 0 1 5 0 0 0 -5 5 5
2
x -2 0 1 0 0 0 0 0 0 0 1 -1 2
7
x 0 6 0 0 0 0 0 1 0 0 5 -5 10
8
x 0 1 0 0 -2 0 2 0 1 0 -2 2 1
9
x 0 1 0 0 0 0 0 0 0 1 0 0 1
3
x 7 -1 0 1 0 0 -1 0 0 0 1 -1 1
j j Z
[image:48.595.109.532.113.354.2]C − 11 0 0 -1 0 7 0 0 0 -5 5 3
Tabel 35 . Tabel simpleks 35 Iterasi 4
Basis C 4 -2 7 -1 0 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11
1
x 0 1 0 0 0
6 1
6
5 0 0 0
6 5
−
6 5
6 5
2
x -2 0 1 0 0 0 0 0 0 0 1 -1 2
7
x 0 0 0 0 0 -1 -5 1 0 0 10 -10 5
8
x 0 0 0 0 -2
6 1
−
6
7 0 1 0
6 7
6 7
−
6 1
9
x 0 0 0 0 0
6 1
−
6 5
− 0 0 1
6 5
6 5
−
6 1
3
x 7 0 0 1 0
6 1
6 1
− 0 0 0
6 1
6 1
−
6 11
j j Z
C − 0 0 0 -1
6 11
−
6
13 0 0 0
6 25
6 25
−
Penyelesaian optimal untuk PL-relaksasi submasalah 4 adalah : 6 1 12 0 , 6 11 , 2 , 6 5 4 3 2
1 = x = x = x = dengan Z =
x
Sehinggga batas untuk submasalah 4 adalah
6 1 12
≤
Z
Karena kedua penyelesaian ini ada (penyelesaian layak) dan mempunyai nilai-nilai yang bukan bilangan bulat untuk peubah-peubah yang dibatasi bulat, maka kedua submasalah ini tidak terhenti..
Iterasi 3 :
Dengan dua submasalah sisa (3 dan 4) yang dibuat berturutan, maka submasalah dengan batas lebih besar (yaitu submasalah 3, dengan batas
6 1 12 6 1
14 > )dipilih
untuk pencabangan berikutnya. Karena
6 5
1 =
x mempunyai nilai yang bukan bilangan bulat pada penyelesaian optimal untuk PL-relaksasi submasalah ini maka x 1
menjadi peubah pencabangan. (Perhatikan bahwa x sekarang adalah peubah 1
pencabangan yang berulang karena x juga dipilah pada iterasi 1). 1
Hal ini memberikan submasalah baru berikut : Submasalah 5
Maksimumkan Z =4x1−2x2 +7x3 −x4 . . . 2.10
Dengan menyelesaikan submasalah 5 diperoleh :
Tabel 36 . Tabel simpleks36 Iterasi 0
Basis C 4 -2 7 -1 0 0 0 0 0 0 0 B
1
x x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11
5
x 0 1 0 5 0 1 0 0 0 0 0 0 10
6
x 0 1 1 -1 0 0 1 0 0 0 0 0 1
7
x 0 6 -5 0 0 0 0 1 0 0 0 0 0
8
x