BIPLOT BIASA DAN KANONIK UNTUK PEMETAAN
PROVINSI BERDASARKAN PRESTASI MAHASISWA IPB
KUSNANDAR
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis berjudul Biplot Biasa dan Kanonik untuk Pemetaan Provinsi Berdasarkan Prestasi Mahasiswa IPB adalah karya saya sendiri dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan oleh pihak lain telah penulis sebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Agustus 2011
ABSTRACT
KUSNANDAR. Ordinary and Canonical Biplots for Province Mapping Based on IPB Students’ Achievement. Supervised by SISWADI and N. K. KUTHA ARDANA.
Biplot is a graphical display of the rows and columns of a data matrix. Ordinary biplot is the biplot that was introduced by Gabriel (1971). The most general method for discrimination among groups using multiple observed variables is canonical variate analysis (CVA). CVA allows us to derive linear combinations
that successively maximize the ratio of ‘between-groups’ to ‘pooled within-group’ sample variance. Biplot representation for CVA is called canonical biplot. Ordinary and canonical biplots are multivariate analyses that can be used for mapping of objects. Procrustes analysis is an analysis tool based on the principle of least squares that can be used to measure the maximum similarity of point of configurations through a series of linear transformations of translation, rotation and dilation. Unfortunately, implementation of canonical biplot and goodness of fit of two matrix configurations with Procrustes analysis has not yet been integrated in statistical package program. The objectives of this study are to examine ordinary biplot, canonical biplot and Procrustes analysis; implement the canonical biplot and Procrustes analysis using functional programming techniques; and compare provincial mapping using ordinary biplot analysis with the analysis of canonical biplot based on IPB students’ achievement. As the first result this study, a program has been written using software Mathematica 8.0 to integrate the ordinary and canonical biplot with Procrustes analysis. For implementation purposes, the data used in this study are IPB students’ achievement in 2009/2010 academic year. Province mapping is an important effort to get an overview of relative position of the province compared to other provinces based on students’ academic achievement. The results from Procrustes analysis of the data matrix with its matrix approximation show that in this case the canonical biplot relatively more suitable to be used. The goodness of fit of configuration of ordinary and canonical biplot with Procrustes analysis is relatively high for data, as well as variables and objects, i.e. more than 91%. This means that the results of ordinary and canonical biplot analysis for mapping the province based on TPB IPB students’ achievement showed relatively more similarities than differences. Extreme difference of the object's position (province) of variables is the province of Sulawesi Utara, Jawa Barat, Banten and Sumatera Selatan in ordinary biplot has superior in Bahasa Indonesia and Pengantar Ilmu Pertanian course, whereas the canonical biplot has superior in Bahasa Inggris and Pendidikan Kewarganegaraan course.
RINGKASAN
KUSNANDAR. Biplot Biasa dan Kanonik untuk Pemetaan Provinsi Berdasarkan Prestasi Mahasiswa IPB. Dibimbing oleh SISWADI and N. K. KUTHA ARDANA.
Analisis biplot merupakan salah satu bentuk Analisis Peubah Ganda (APG) yang dapat memberikan gambaran secara grafik dari suatu matriks data tentang kedekatan antar objek, keragaman peubah, korelasi antarpeubah serta keterkaitan objek dengan peubah. Biplot biasa yang dipelajari dalam penelitian ini adalah biplot yang diperkenalkan oleh Gabriel (1971), sedangkan biplot kanonik merupakan representasi grafis dari analisis peubah kanonik (APK, Canonical Variate Analysis). APK merupakan analisis data dengan peubah ganda yang berbasis analisis pengelompokan data, digunakan untuk memperoleh kombinasi linear dari peubah-peubah asal yang akan memberikan nilai sedekat mungkin bagi objek-objek dalam kelompok yang sama dan sebesar mungkin bagi objek-objek antarkelompok.
Analisis biplot menghasilkan tiga matriks pendekatan yang terkait dengan data, peubah, dan objek. Ketepatan matriks pendekatan tersebut pada biplot biasa ditelusuri menggunakan ukuran kesesuaian dari Gabriel (2002) dan analisis Procrustes sedangkan pada biplot kanonik menggunakan analisis Procrustes. Analisis Procrustes merupakan alat analisis berdasarkan asas kuadrat terkecil yang dapat digunakan untuk mengukur kemiripan maksimal antarkonfigurasi titik melalui serangkaian transformasi linear yaitu translasi, rotasi dan dilasi.
Biplot biasa dengan sistem perintah telah terintegrasi ke dalam beberapa program paket statistika seperti SAS, R dan Stata serta telah diimplementasikan ke dalam paket sistem aljabar komputer Mathematica dengan teknik pemrograman fungsional berbasis GUI (Graphical User Interface). Tetapi, implementasi biplot kanonik dan ukuran kesesuaian dua konfigurasi menggunakan analisis Procrustes dengan sistem perintah belum terintegrasi dalam program paket statistika.
Biplot biasa maupun kanonik dapat memberikan gambaran yang lebih terinci dalam pemetaan provinsi dalam bidang pendidikan sehingga informasi yang diperoleh merupakan gambaran perbandingan mutu pendidikan suatu provinsi dengan provinsi lainnya. Mahasiswa IPB hampir mewakili seluruh provinsi di Indonesia, diharapkan mampu memberikan gambaran prestasi dan pemetaan mutu pendidikan setiap daerahnya. Berdasarkan uraian diatas, tujuan penelitian ini ialah untuk mengkaji analisis biplot biasa, biplot kanonik dan analisis Procrustes; mengimplementasikan analisis biplot kanonik dan ukuran kesesuaian dua konfigurasi matriks dengan analisis Procrustes menggunakan teknik pemrograman fungsional; dan membandingkan pemetaan provinsi menggunakan analisis biplot biasa dengan analisis biplot kanonik berdasarkan prestasi mahasiswa IPB.
TPB IPB yang mewakilinya, yaitu Sulawesi Tengah) asal sekolah menengahnya serta data nilai mutu mata kuliah dan IPK mahasiswa TPB IPB tahun akademik 2009/2010 yang diperoleh dari Direktorat Pendidikan Tingkat Persiapan Bersama Institut Pertanian Bogor. Sebagai penyederhanaan dan meningkatkan ketepatan model pada analisis maka dilakukan proses seleksi peubah pada data asal yaitu proses pengidentifikasian dan pengurangan peubah-peubah yang memberikan kontribusi informasi yang relatif kecil pada keragaman data.
Penelitian ini menghasilkan paket BiplotKanonik dan GFProcrustes sebagai implementasi dari biplot kanonik dan ukuran kesesuaian dua konfigurasi menggunakan analisis Procrustes dengan teknik pemrograman fungsional Mathematica.
Analisis Procrustes antara matriks data dengan matriks pendekatannya menghasilkan ukuran kesesuaian pada biplot kanonik relatif lebih besar dari pada biplot biasa untuk data dan peubah, tetapi untuk objek relatif sama. Hal ini mengindikasikan bahwa dalam kasus ini biplot kanonik relatif lebih layak digunakan. Sedangkan analisis Procrustes antara matriks koordinat biplot biasa dengan koordinat biplot kanonik menghasilkan ukuran kesesuaian yang cukup tinggi untuk data, peubah maupun objek, yaitu di atas 91%. Hal ini berarti bahwa hasil dari analisis biplot biasa dan kanonik untuk pemetaan provinsi berdasarkan prestasi mahasiswa TPB IPB memperlihatkan relatif lebih banyak persamaan dari pada perbedaannya.
Perbedaan yang ekstrem dari posisi objek (provinsi) terhadap peubah ialah provinsi Sulawesi Utara, Jawa Barat, Banten dan Sumatera Selatan pada biplot biasa memiliki keunggulan pada mata kuliah Bahasa Indonesia dan Pengantar Ilmu Pertanian, sedangkan pada biplot kanonik memiliki keunggulan pada mata kuliah Bahasa Inggris dan Pendidikan Kewarganegaraan.
Interpretasi biplot kanonik untuk pemetaan provinsi berdasarkan prestasi mahasiswa TPB IPB memberikan gambaran bahwa provinsi Kalimantan Timur dan Kepulauan Bangka Belitung memiliki keunggulan pada semua mata kuliah. Provinsi Kalimantan Selatan, Bengkulu dan Daerah Istimewa Yogyakarta memiliki keunggulan pada mata kuliah Pendidikan Kewarganegaraan, Bahasa Indonesia, Bahasa Inggris dan Ekonomi Umum. Provinsi Jawa Tengah, Jawa Timur dan Kepulauan Riau memiliki keunggulan pada mata kuliah Pengantar Matematika, Fisika, Biologi dan Pengantar Ilmu Pertanian. Provinsi Gorontalo, Lampung, Jambi, Nusa Tenggara Timur, Papua Barat, Kalimantan Barat, Sulawesi Barat memiliki keunggulan pada mata kuliah Pengantar Matematika dan Pengantar Ilmu Pertanian. Provinsi Sulawesi Utara, Nusa Tenggara Barat, Jawa Barat, Banten dan Sumatera Selatan memiliki keunggulan pada mata kuliah mata kuliah Bahasa Inggris dan Pendidikan Kewarganegaraan. Provinsi Sumatera Barat, DKI Jakarta, Bali dan Riau merupakan provinsi-provinsi yang memiliki prestasi rata-rata pada semua mata kuliah. Sedangkan provinsi Sumatera Utara, Sulawesi Tenggara, Sulawesi Selatan, Kalimantan Tengah, Aceh, Papua, Maluku Utara dan Maluku memiliki prestasi di bawah rata-rata untuk semua mata kuliah. Kata Kunci: biplot biasa, analisis peubah kanonik, biplot kanonik, analisis
©Hak Cipta milik Institut Pertanian Bogor, tahun 2011 Hak Cipta dilindungi Undang-Undang
1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.
a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik dan tinjauan suatu masalah.
b. Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor.
BIPLOT BIASA DAN KANONIK UNTUK PEMETAAN
PROVINSI BERDASARKAN PRESTASI MAHASISWA IPB
KUSNANDAR
Tesis
Sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada
Program Studi Matematika Terapan
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Judul Tesis : Biplot Biasa dan Kanonik untuk Pemetaan Provinsi Berdasarkan Prestasi Mahasiswa IPB
Nama : Kusnandar
NRP : G551090081
Disetujui Komisi Pembimbing
Dr. Ir. Siswadi, M. Sc. Ir. N. K. Kutha Ardana, M. Sc. Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan
Dr. Ir. Endar H. Nugrahani, M. S. Dr. Ir. Dahrul Syah, M. Sc. Agr.
KATA PENGANTAR
Puji dan syukur penulis panjatkan ke hadirat Allah SWT yang telah melimpahkan rahmat dan hidayah-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Pebruari 2011 ini ialah biplot, dengan judul Biplot Biasa dan Kanonik untuk Pemetaan Provinsi Berdasarkan Prestasi Mahasiswa IPB.
Terima kasih penulis ucapkan kepada Bapak Dr. Ir. Siswadi, M. Sc. dan Ir. N.K. Kutha Ardana, M. Sc. yang telah membimbing dengan penuh ketekunan dan kesabaran hingga selesainya penulisan karya ilmiah ini serta Ibu Dr. Ir. Endar H. Nugrahani, M. S. selaku penguji luar komisi yang telah banyak memberikan saran. Di samping itu, penghargaan penulis sampaikan kepada Bapak Dr. Ir. Ibnul Qayim selaku Direktur TPB IPB yang telah memberikan bantuan data nilai mata kuliah dan IPK mahasiswa TPB IPB tahun akademik 2009/2010, Bapak Donny Citra Lesmana, S.Si., M. Fin. Math. yang telah membantu dalam hal pengadaan referensi serta seluruh dosen dan staf pegawai Departemen Matematika FMIPA IPB atas segala bantuannya. Ucapan terima kasih juga penulis sampaikan pada Kemenag RI yang telah membiayai penelitian ini. Ungkapan terima kasih juga disampaikan kepada kedua orang tua, istri, anak-anak dan seluruh keluarga yang telah memberikan dukungan, pengertian, doa dan kasih sayangnya serta rekan-rekan dan semua pihak yang telah membantu penulis, yang tidak dapat penulis sebutkan satu persatu.
Penulis menyadari bahwa karya ilmiah ini masih jauh dari sempurna, untuk itu saran yang membangun sangat penulis harapkan. Semoga karya ilmiah ini bermanfaat.
RIWAYAT HIDUP
Penulis dilahirkan di Kabupaten Cirebon pada tanggal 29 September 1978 dari ayah Tjarba dan ibu Rumsiti. Penulis merupakan putra kedua dari empat bersaudara.
DAFTAR ISI
Halaman
DAFTAR TABEL ... xii
DAFTAR GAMBAR ... xiii
DAFTAR LAMPIRAN ... xiv
PENDAHULUAN Latar Belakang ... 1
Tujuan Penelitian ... 3
TINJAUAN PUSTAKA Analisis Biplot Biasa ... 5
Ukuran Kesesuaian Biplot Biasa ... 10
Analisis Peubah Kanonik ... 11
Analisis Biplot Kanonik ... 15
Analisis Procrustes ... 19
METODE PENELITIAN Sumber Data ... 25
Peubah Penelitian ... 25
Objek Penelitian ... 26
Metode Penelitian ... 27
HASIL DAN PEMBAHASAN Implementasi Biplot Kanonik dan Analisis Procrustes dengan Mathematica ... 29
Eksplorasi Data ... 31
Gambaran Umum Provinsi ... 35
Seleksi Peubah ... 36
Analisis Biplot Kanonik dan Kanonik Data Asal ... 37
Analisis Biplot Kanonik dan Kanonik dengan Seleksi Peubah ... 45
KESIMPULAN DAN SARAN Kesimpulan ... 53
Saran ... 54
DAFTAR PUSTAKA ... 55
DAFTAR TABEL
Halaman
1 Analisis ragam antarkelompok dan dalam kelompok ... 12
2 Peubah penelitian ... 25
3 Konversi huruf mutu ... 26
4 Provinsi asal mahasiswa dan banyak mahasiswa yang mewakilinya ... 26
5 Sebaran nilai akhir mata kuliah TPB IPB tahun akademik 2009/2010 ... 31
6 Ukuran pemusatan dan penyebaran nilai mata kuliah dan IPK mahasiswa TPB IPB tahun akademik 2009/2010 ... 32
7 Matriks korelasi Pearson data asal ... 34
8 Ukuran kesesuaian biplot biasa dan kanonik data asal ... 39
9 Ukuran kesesuaian koordinat biplot biasa dan kanonik data asal ... 39
10 Ukuran kesesuaian biplot biasa dan kanonik dengan seleksi peubah ... 47
DAFTAR GAMBAR
Halaman
1 Diagram kotak garis nilai mata kuliah dan IPK ... 33
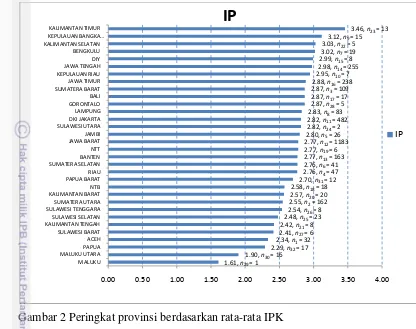
2 Peringkat provinsi berdasarkan rata-rata IPK ... 36
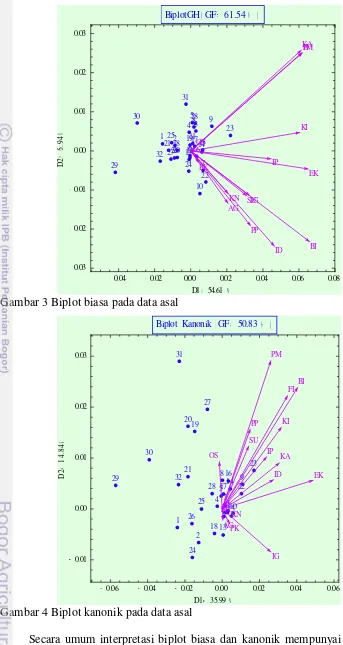
3 Biplot biasa pada data asal ... 38
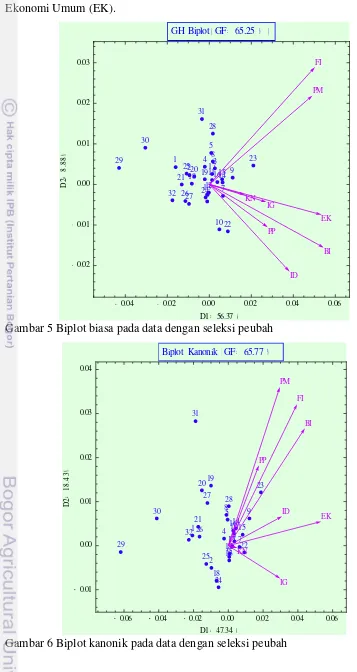
4 Biplot kanonik pada data asal ... 38
5 Biplot biasa pada data dengan seleksi peubah ... 46
DAFTAR LAMPIRAN
Halaman
1 Program paket BiplotKanonik ... 59
2 Program paket GFProcrustes ... 60
3 Statistik deskriptif data asal ... 61
4 Tabel nilai rata-rata mata kuliah dan IPK mahasiswa TPB IPB tahun akademik 2009/2010 ... 62
5 Korelasi Pearson data asal ... 63
6 Eigenanalisis dari analisis komponen utama berbasis matriks koragam .... 64
7 Peringkat provinsi berdasarkan rata-rata IPK ... 65
8 Biplot biasa pada data asal ... 66
9 Biplot kanonik pada data asal ... 67
10 Biplot biasa pada data dengan seleksi peubah ... 68
11 Biplot kanonik pada data dengan seleksi peubah ... 69
12 Matriks koordinat biplot biasa pada data asal ... 70
13 Matriks koordinat biplot kanonik pada data asal ... 71
14 Matriks koordinat biplot biasa pada data dengan seleksi peubah ... 72
15 Matriks koordinat biplot kanonik pada data dengan seleksi peubah ... 73
16 Matriks jumlah kuadrat dan hasil kali data dengan seleksi peubah ... 74
17 Matriks jumlah kuadrat dan hasil kali data antarkelompok pada data asal .. 75
PENDAHULUAN
Latar Belakang
Dalam kehidupan sehari-hari seringkali dijumpai pengamatan yang melibatkan lebih dari satu peubah (peubah ganda) sehingga sulit untuk diinterpretasikan secara langsung. Oleh karena itu perlu dilakukan pereduksian dimensi data peubah yang cukup banyak tersebut menjadi peubah yang lebih sederhana dengan tetap mempertahankan informasi peubah asalnya. Analisis Peubah Ganda (APG) merupakan analisis statistika yang melakukan analisis secara serempak terhadap peubah ganda tersebut. Dengan menyertakan lebih dari satu peubah dengan keterkaitannya, diharapkan akan dapat memberikan tambahan informasi daripada bila hanya dilakukan pada masing-masing peubah secara terpisah (Siswadi dan Suharjo, 1999). Selain itu melalui analisis peubah ganda juga dapat dilihat pengelompokan objek berdasarkan kemiripan peubah-peubah penyusunnya.
Analisis biplot merupakan salah satu teknik yang populer dalam analisis data peubah ganda. Biplot pertama kali diperkenalkan oleh Gabriel (1971). Analisis ini merupakan salah satu bentuk APG yang dapat memberikan gambaran secara grafik tentang keragaman peubah, kedekatan antarobjek serta keterkaitan peubah dengan objek yang dapat digunakan untuk menggambarkan sebuah tabel ringkasan dengan banyak peubah agar lebih menarik, informatif, komunikatif dan artistik. Dari biplot diperoleh tiga matriks pendekatan yang terkait dengan data, peubah, dan objek. Ukuran kesesuaian dari ketiga matriks tersebut dikemukakan oleh Gabriel (2002).
Analisis Procrustes adalah alat analisis berdasarkan asas kuadrat terkecil yang dapat digunakan untuk mengukur kemiripan maksimal antarkonfigurasi titik melalui serangkaian transformasi linear (Bakhtiar dan Siswadi, 2011). Bentuk transformasi tersebut adalah translasi, rotasi dan dilasi. Analisis ini bertujuan untuk membandingkan dua konfigurasi yang mewakili unit pengamatan yang sama sebagai nilai numerik. Nilai numerik yang dihasilkan dapat digunakan sebagai ukuran kesesuaian (goodness of fit) antarkonfigurasi. Untuk melihat kesamaan bentuk dan ukuran dari dua konfigurasi maka setelah kedua konfigurasi dilakukan translasi salah satu konfigurasi dibuat tetap sementara konfigurasi yang lainnya ditransformasikan sehingga paling sesuai dengan konfigurasi pertama.
Biplot biasa dengan sistem perintah telah terintegrasi ke dalam beberapa program paket statistika seperti SAS, R dan Stata. Sejalan dengan makin berkembangnya teknik komputasi dengan sistem aljabar komputer (SAK), biplot biasa telah diimplementasikan ke dalam paket SAK Mathematica dengan teknik pemrograman fungsional berbasis GUI (Graphical User Interface) (Ardana dan Siswadi, 2009). Tetapi, implementasi biplot kanonik dan ukuran kesesuaian dua konfigurasi menggunakan analisis Procrustes dengan sistem perintah belum terintegrasi dalam suatu program paket statistika.
salah satunya dipengaruhi oleh mutu masukan, di mana seleksi penerimaan mahasiswa baru program sarjana IPB dilakukan dengan prinsip education for everyone yang pada tahun akademik 2009/2010 dilaksanakan melalui 5 (lima) jalur, yaitu: (1) Undangan Seleksi Masuk IPB (USMI); (2) Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN); (3) Undangan khusus bagi lulusan SMA yang mempunyai prestasi nasional maupun internasional; (4) Seleksi Penerimaan Mahasiswa Beasiswa Utusan Daerah (BUD); dan (5) Ujian Talenta Mandiri (UTM). Hasil seleksi tersebut menunjukkan mahasiswa yang menuntut ilmu di IPB sangat beragam latar belakang kualitas pendidikan antarsekolah dan antarprovinsinya.
Suatu analisis diperlukan untuk memperoleh gambaran yang lebih terinci dalam pemetaan provinsi sehingga informasi yang diperoleh merupakan gambaran mutu pendidikan di sekolah menengah masing-masing provinsi berdasarkan prestasi mahasiswa TPB IPB. Pengamatan lebih dari satu peubah (peubah ganda) dianalisis secara serempak menggunakan APG, salah satunya adalah dengan analisis biplot. Dalam analisis biplot biasa, data yang merepresentasikan provinsi sebagai gambaran objek dan mata kuliah sebagai gambaran peubah dari sejumlah mahasiswa berupa data asal tanpa melakukan proses manipulasi (data disagregat). Sedangkan dalam analisis biplot kanonik data diperoleh dengan mencari rata-ratanya untuk setiap provinsi kemudian ditransformasikan dengan memperhitungkan banyak objek dan keragaman dalam setiap provinsi.
Tujuan Penelitian
Tujuan penelitian ini ialah:
1. Mengkaji analisis biplot biasa, biplot kanonik dan analisis Procrustes.
2. Mengimplementasikan analisis biplot kanonik dan ukuran kesesuaian dua konfigurasi matriks dengan analisis Procrustes menggunakan teknik pemrograman fungsional.
TINJAUAN PUSTAKA
Analisis Biplot Biasa
Analisis biplot merupakan suatu upaya untuk memberikan peragaan grafik dari matriks data dalam suatu plot dengan menumpangtindihkan vektor-vektor dalam ruang berdimensi rendah, biasanya dua (atau tiga) yang mewakili vektor-vektor baris matriks (gambaran objek) dengan vektor-vektor yang mewakili kolom matriks (gambaran peubah). Dari peragaan ini diharapkan diperoleh gambaran tentang objek, misalnya kedekatan antarobjek, gambaran tentang peubah, baik tentang keragamannya maupun korelasinya, serta keterkaitan antara objek-objek dengan peubah-peubahnya. Tampilan objek dalam analisis komponen utama (AKU, Principal Components Analysis) merupakan kasus khusus dari analisis biplot dan penghitungan dalam analisis biplot didasarkan pada penguraian nilai singular (PNS, Singular Value Decomposition) suatu matriks (Siswadi dan Suharjo, 1999).
Informasi yang dapat diperoleh dari analisis biplot antara lain tentang: 1. Kedekatan antarobjek. Informasi ini dapat dijadikan panduan untuk
mengetahui objek yang memiliki kemiripan karakteristik dengan objek lain. Dua objek yang memiliki karakteristik sama akan digambarkan sebagai dua titik dengan posisi yang berdekatan.
2. Keragaman peubah. Informasi ini digunakan untuk melihat apakah ada peubah yang memiliki nilai keragaman yang hampir sama. Peubah dengan keragaman kecil digambarkan dengan vektor yang pendek, sebaliknya jika keragamannya besar digambarkan dengan vektor yang panjang.
4. Keterkaitan peubah dengan objek. Informasi ini digunakan untuk melihat keunggulan dari setiap objek. Objek yang letaknya searah vektor peubah, menunjukkan objek tersebut nilainya di atas rata-rata, jika berlawanan arah berarti nilainya di bawah rata-rata, jika hampir di tengah-tengah berarti nilainya mendekati rata-rata.
Analisis Biplot adalah peragaan secara grafik dari baris dan kolom sebuah matriks data , dengan baris mewakili objek dan kolom mewakili peubah. Dalam setiap aplikasi, analisis biplot dimulai dengan mentransformasikan matriks sebagai matriks data asal yang terkoreksi terhadap nilai rata-rata kolomnya menjadi matriks yang akan digambarkan (Aitchison dan Greenacre, 2001),
11' ,
dengan 1 adalah vektor berukuran n×1 yang semua elemennya bernilai 1. Matriks koragam yang diperoleh dari matriks ialah:
adalah matriks diagonal dengan
elemen diagonal utama 1 sii ; i = 1,2, . . ., p. Elemen juga merupakan kosinus dan jarak Mahalanobis antara objek ke-i dan ke-j adalah:
.
Apabila matriks berpangkat r dengan r ≤ min {n, p} maka dengan menggunakan PNS matriks dapat diuraikan menjadi:
dengan adalah matriks diagonal yang elemen diagonal utamanya merupakan akar dari eigennilai-eigennilai positif matriks atau , yaitu = diag ( , , ..., ), dengan > 0. Nilai disebut nilai singular dari dan merupakan eigennilai-eigennilai positif matriks atau . Matriks dan adalah matriks ortonormal kolom, sehingga (matriks identitas berdimensi r). Matriks adalah matriks yang kolom-kolomnya merupakan eigenvektor yang bersesuaian dengan eigennilai positif dari matriks , yaitu dan adalah matriks yang kolom-kolomnya merupakan eigenvektor-eigenvektor yang bersesuaian dengan eigennilai-eigennilai positif dari matriks , yaitu .
Teorema Eckart-Young (Aitchison dan Greenacre, 2001) menyatakan bahwa jika matriks dihitung dengan s pertama nilai dan vektor singular yang bersesuaian, sebagai contoh untuk s = 2 :
=
,
kemudian karena matriks sebagai pendekatan terbaik bagi maka :
menjadi minimum, dengan merupakan notasi dari norma Frobenius.
Dalam Jolliffe (2002), dengan mendefinisikan dan , maka untuk α [0,1]:
, dan elemen ke-( ) dari matriks dapat ditulis:
,
dengan merupakan vektor baris ke-i dari matriks , i = 1, 2, …, n dan merupakan vektor baris ke-j dari matriks , j= 1, 2, …, p; di mana vektor dan
mempunyai r elemen.
(7)
(8)
(9)
(10)
Untuk menggambarkan pada ruang dimensi s < r, dapat didekati dengan menggunakan matriks berpangkat s,
=
= .
Biasanya digunakan s = 2, sehingga koordinat-koordinat dan dapat digambarkan dalam ruang berdimensi dua (Lipkovich dan Smith, 2002).
Pengambilan nilai α tertentu berimplikasi penting dalam interpretasi biplot. Secara umum untuk setiap nilai α yang digunakan, penumpangtindihan vektor dan yang diplot pada ruang yang sama diperoleh nilai amatan peubah ke-j pada objek ke-i yang telah dikoreksi terhadap nilai tengahnya yaitu . Nilai amatan tersebut bertanda positif bila kedua vektor tersebut searah, yaitu sudut kedua vektor tersebut ada dalam [0, ), bertanda negatif bila kedua vektor tersebut berlawanan arah, yaitu sudut kedua vektor tersebut ada dalam ( , ] dan bernilai nol bila kedua vektor tersebut saling tegak lurus, yaitu sudut kedua vektor tersebut . Posisi relatif titik-titik dan akan memberikan informasi tentang objek-objek yang mempunyai nilai relatif besar, rataan, atau kecil dari peubah-peubah yang diamati.
1. Jika α = 0, maka dan , akibatnya :
, sehingga diperoleh:
a. , dengan adalah koragam peubah ke-i dan ke-j. Artinya, penggandaan titik antara vektor dan akan memberikan gambaran koragam antara peubah ke-i dan ke-j.
b. = , = , artinya panjang vektor tersebut akan memberikan gambaran tentang keragaman peubah ke-i. Makin panjang vektor dibandingkan dengan vektor maka makin besar keragaman peubah dibanding peubah .
(12)
c. Korelasi antara peubah ke-i dan ke-j dijelaskan oleh kosinus sudut antara dan (misalnya : θ), yaitu :
cos =
=
= .
Berdasarkan sudut yang dibentuk antara vektor dan , korelasi peubah ke-i dan ke-j dapat dijelaskan sebagai berikut:
1) semakin besar korelasi positifnya jika θ mendekati 0, dan korelasi sama dengan 1 jika θ = 0,
2) semakin besar korelasi negatifnya jika θ mendekati π, dan korelasi sama dengan -1 jika θ = π, dan
3) semakin kecil korelasi positif dan negatifnya jika θ mendekati dan tidak berkorelasi apabila θ = .
d. Jika Xberpangkat p maka
, dengan adalah
matriks koragam yang diperoleh dari . Berarti kuadrat jarak Euclid antara vektor dan pada biplot sebanding dengan kuadrat jarak Mahalanobis antara vektor dan (Siswadi dan Suharjo, 1999).
2. Jika α =1, maka dan atau ; akibatnya:
, sehingga diperoleh
a. , artinya kuadrat jarak Euclid antara dan akan samadengan kuadrat jarak Euclid antara dan . b. Posisi dalam plot akan sama dengan posisi objek ke-i dengan
menggunakan r komponen utama pertama.
c. Vektor kolom sama dengan vektor yang merupakan koefisien untuk komponen utama ke-j.
(14)
Dari interpretasi biplot di atas, penguraian tidak bersifat khas. Jika
α = 1 maka g-plot diperoleh dengan memisalkan dan , baris ke-i matriks akan digunakan untuk merepresentasikan baris ke-i matriks , yang berarti merepresentasikan objek ke-i, sedangkan baris ke-j matriks akan digunakan untuk merepresentasikan kolom ke-j matriks , yang berarti merepresentasikan peubah ke-j. Sedangkan jika α = 0 maka h-plot diperoleh dengan memisalkan dan yang merupakan gambaran ragam dan korelasi di dalam grafik.
Ukuran Kesesuaian Biplot Biasa
Menurut Gabriel (2002), biplot tidak hanya sebagai pendekatan matriks data dengan menggunakan matriks , tetapi juga koragam dan korelasi antarpeubah, serta kemiripan antarobjek. sebagai pendekatan dari matriks terkait pada matriks koragam dan korelasi antarpeubah, sedangkan matriks sebagai pendekatan bagi terkait pada ukuran kemiripan objek.
Rumus umum yang dikemukakan oleh Gabriel untuk ukuran kesesuaian biplot (Goodness of Fit of Biplot) adalah sebagai berikut
,
dengan dan adalah suatu matriks, di mana merupakan pendekatan . Ukuran kesesuaian biplot sebagai ukuran kedekatan dari tiga bentuk matriks, yaitu:
1. Kesesuaian data : GF
.
2. Kesesuaian peubah : GF
.
3. Kesesuaian objek : GF
.
Makin besar (mendekati 100%) nilai ukuran kesesuaian untuk memperoleh gambaran layak tidaknya analisis biplot dalam ruang dimensi s dengan matriks sebagai matriks pendekatan terbaik berpangkat s, makin sesuai matriks pendekatannya merepresentasikan matriks awalnya dan karenanya makin layak analisis biplot digunakan untuk penarikan kesimpulan (Siswadi dan Suharjo, 1999).
(16)
Analisis Peubah Kanonik
Pendekatan standar untuk perlakuan data peubah ganda dengan beberapa objek diidentifikasi a priori, kelompok memiliki sejarah panjang dalam literatur statistika, adalah analisis peubah kanonik (APK, Canonical Variate Analysis) yang diperkenalkan oleh Fisher (1936). APK merupakan salah satu teknik statistika untuk analisis data dengan peubah ganda yang berbasis analisis pengelompokan data sehingga ragam antarkelompok maksimum dan ragam di dalam kelompok minimum (Varas etal. 2005).
Salah satu pendekatan dalam APK ialah mencari peubah kanonik yang merupakan kombinasi linear dari peubah asal yang akan menghasilkan cara terbaik dalam pemisahan kelompok-kelompok tersebut. Peubah ini akan memberikan nilai sedekat mungkin bagi objek-objek dalam kelompok yang sama dan sebesar mungkin bagi objek-objek antarkelompok.
Andaikan ada n objek dari m kelompok contoh acak dengan masing-masing berukuran n1, n2, ..., nm (n1 + n2 + ... + nm = n) dengan p peubah yang diamati,
X1, X2, ..., Xp. Misalnya = ( X1, X2, ..., Xp) adalah vektor yang mewakili peubah, adalah matriks data asal yang telah terkoreksi terhadap nilai rata-rata
kolomnya, dan adalah matriks indikator m kelompok (peubah dummy) yang diberikan oleh:
.
Definisikan:
= diag (n1, n2, ..., nm),
yaitu matriks diagonal berukuran m×m dengan elemen diagonal utamanya merupakan banyak objek dari setiap kelompok dan m p merupakan matriks yang
setiap barisnya merupakan vektor rata-rata dari peubah dalam setiap kelompok, yaitu:
.
Analisis ragam antarkelompok dan dalam kelompok dapat dikonstruksi seperti pada Tabel 1.
(20)
(21)
Tabel 1 Analisis ragam antarkelompok dan dalam kelompok products) data dalam kelompok dapat ditulis juga sebagai:
, . Sedangkan matriks JKK data antarkelompok dapat ditulis sebagai:
,
dengan merupakan rata-rata keseluruhan dari peubah j, yaitu dan .
Tujuannya, berdasarkan pengukuran peubah X1, X2, ..., Xp secara serempak,
akan memaksimumkan rasio antara ragam antarkelompok dengan ragam dalam kelompok. Untuk mencapai tujuan ini, transformasikan peubah vektor x, ke dalam peubah baru, yang membuat ragam yang tinggi antarkelompok terhadap ragam dalam kelompok. Jika transformasi dilambangkan oleh , maka yang akan dicari adalah vektor sehingga
maksimum dengan kendala
, yaitu solusi dibatasi untuk vektor dengan panjang satu satuan terhadap matriks . Fungsi yang akan dimaksimumkan merupakan rasio antara ragam antarkelompok dengan ragam dalam kelompok. Ini adalah fungsi homogen berderajat nol di dan invarian terhadap perubahan skala.
(25) (23)
Sekarang akan dicari vektor yang dapat memaksimumkan fungsi , dengan kendala . Menggunakan pengali Lagrange, berarti yang akan dimaksimumkan adalah fungsi
, sehingga,
,
(27)
(28)
, atau
. (29)
Ini berarti maksimum yang dicari adalah
Matriks merupakan matriks nonsingular, sehingga dengan mengalikan persamaan (27) dengan , diperoleh
. (30)
Artinya, vektor atau bobot kanonik yang dapat memaksimumkan adalah eigenvektor dari matriks yang bersesuaian dengan eigennilai terbesar . Transformasi yang diperoleh dari eigenvektor yang bersesuaian dengan eigennilai terbesar disebut peubah kanonik pertama. Peubah kanonik kedua diperoleh dari eigenvektor yang bersesuaian dengan eigennilai terbesar kedua, dan begitu pula untuk mencari peubah kanonik yang lainya. Banyaknya peubah kanonik yang mungkin diperoleh adalah r = pangkat ( = min (p, m– 1).
Semua penyelesaian dari (28) dapat dikumpulkan bersama dalam bentuk
, (31)
dengan dan = diag ( , , ..., ), di mana ≥ ≥ ...
≥ > 0, sehingga . Jika r = p, maka dapat ditulis sebagai dan . Dengan mengalikan persamaan (31) dengan diperoleh
. (32)
simetris berukuran p×p daripada matriks (Gittins, 1985). Dekomposisi spektral dari matriks simetris diberikan oleh:
, (33)
dengan adalah suatu matriks berukuran p×p yang elemen-elemennya eigenvektor dan adalah matriks diagonal yang memiliki eigennilai pada diagonal utamanya.
Berdasarkan asumsi tersebut persamaan (27) dapat ditulis menjadi
.
Jadi, persamaan tersebut dapat ditulis sebagai
, (34)
dengan dan = 1.
Persamaan (34) menyatakan bahwa adalah eigenvektor dari matriks
yang bersesuaian dengan eigennilai dan = ,
sehingga, .
Semua kombinasi linear untuk sebuah objek dengan nilai-nilai diberikan oleh:
. (35)
Hal ini memberikan sebuah transformasi dari peubah asal menjadi himpunan peubah baru yang dikenal sebagai peubah kanonik. Ruang yang dihasilkan oleh peubah-peubah ini disebut ruang kanonik. Rata-rata kelompok pada ruang kanonik disebut juga rata-rata kanonik diberikan oleh:
, (36)
dan transformasi seluruh himpunan objek pada ruang kanonik diberikan oleh . Sehingga:
. (37)
Peubah kanonik yang diperoleh, y1, y2, …, yrmerupakan kombinasi linear
yang dipilih sehingga y1 merefleksikan perbedaan terbesar antarkelompok, peubah
y2 merefleksikan perbedaan terbesar antarkelompok yang tidak dapat dicakup oleh
y1, peubah y3 merefleksikan perbedaan terbesar antarkelompok yang tidak dapat
dicakup oleh y1 dan y2, dan seterusnya. Diharapkan beberapa peubah kanonik
pertama, misalnya dua peubah kanonik pertama, cukup layak digunakan sehingga masing-masing objek dan rataannya dapat digambarkan dalam ruang berdimensi dua. Bila hal ini dimungkinkan maka bagaimana baiknya upaya pemisahan antarkelompok dan penentuan objek ke suatu kelompok akan lebih mudah dilakukan.
Analisis Biplot Kanonik
Analisis biplot kanonik merupakan representasi grafik dari APK, dikembangkan oleh Gabriel (1995) untuk memperoleh representasi secara serempak antara rata-rata kelompok dan peubah di mana dimungkinkan tidak hanya untuk menetapkan perbedaan antarkelompok tetapi juga untuk menggambarkan peubah yang dianggap dominan dalam membedakan antarkelompok (Vallejo-Arboleda et al. 2007).
Misalnya adalah matriks data asal yang terkoreksi terhadap rata-rata kolomnya dan adalah matriks indikator m kelompok (peubah dummy). Analisis biplot kanonik merupakan peragaan secara grafik dari baris dan kolom sebuah matriks , dengan baris mewakili rata-rata kelompok dan kolom mewakili peubah. Matriks merupakan rata-rata objek masing-masing kelompok untuk setiap peubah yang diamati dan terkoreksi terhadap nilai rata-rata keseluruhan.
Untuk memperhitungkan pengaruh penyebaran objek dan skala pengukuran peubah, diperkenalkan pembobotan sehubungan dengan matriks JKK data dalam kelompok dan yang lainnya berkaitan dengan banyaknya objek, hal ini karena akurasi rata-rata tergantung pada ukuran yang telah dihitung, sehingga dapat didefinisikan:
Artinya, baris dari terboboti oleh banyaknya objek dan peubah pada kolom terboboti oleh invers dari matriks JKK dalam kelompok (Gabriel, 1972), dengan
, (39)
sehingga memiliki eigenvektor dan eigennilai , dengan
.
Mengkonstruksi biplot dari matriks dengan ukuran tersebut akan setara dengan mengkonstruksi biplot untuk matriks . Biplot representasi dari matriks diperoleh dari PNS, yaitu
, (40)
dengan adalah matriks diagonal yang elemen diagonal utamanya merupakan
akar dari eigennilai-eigennilai positif matriks atau , yaitu , dengan . Nilai
disebut nilai singular dari dan merupakan eigennilai-eigennilai positif matriks atau . Matriks dan adalah matriks ortonormal kolom, sehingga (matriks identitas berdimensi r). Matriks adalah matriks yang kolom-kolomnya merupakan eigenvektor yang bersesuaian dengan eigennilai positif dari matriks , yaitu dan adalah matriks yang kolom-kolomnya merupakan eigenvektor-eigenvektor yang bersesuaian dengan eigennilai-eigennilai positif dari matriks , yaitu .
Dari persamaan (39) diperoleh:
. (41)
Penyelesaian untuk diperoleh dengan mensubstitusikan persamaan (38) ke persamaan (40), diperoleh:
atau
, (42)
yang ekuivalen dengan penguraian nilai singular umum (PNSU, Generalized Singular Value Decomposition) dari matriks dalam metrik dan , yaitu:
, (43)
dengan dan . Dengan memilih matriks definit positif dan , sehingga , dan
. PNSU menyediakan pendekatan terbaik
pangkat rendah dari matriks menggunakan nilai dan vektor singular pertama. Penguraian pada (42) memungkinkan untuk mengkonstruksi representasi biplot untuk matriks rata-rata kelompok, yaitu:
, (44)
dengan
, dan ,
di mana . Elemen ke-( ) dari matriks dapat ditulis sebagai:
, (45)
dengan merupakan vektor baris ke-i dari matriks , i = 1, 2, …, n dan merupakan vektor baris ke-j dari matriks , j= 1, 2, …, p; di mana vektor dan
mempunyai r elemen.
Untuk menggambarkan pada ruang dimensi s < r, dapat didekati menggunakan matriks berpangkat s,
= , (46)
Matriks dan pada biplot kanonik memenuhi sifat sebagai berikut: 1. Berdasarkan PNS matriks yang diberikan dalam persamaan (40), diperoleh
, dan
.
Oleh karena itu, matriks dapat dinyatakan dengan mengganti ekspresi P dan pada (38) sebagai:
, (47)
dan mengganti dalam persamaan (41) kemudian mensubstitusikannya ke (47) diperoleh:
. (48)
Persamaan (48) dapat menafsirkan matriks sebagai proyeksi pada daerah pemisahan maksimum dari kelompok, yang dihasilkan oleh kolom dari matriks , dan
(49)
dengan adalah matriks JKK data dalam kelompok, adalah vektor rata-rata dari kelompok i. Artinya, kuadrat jarak Euclid antara vektor dan pada biplot sama dengan kuadrat jarak Mahalanobis antara vektor dan . 2. Perkalian dari penanda baris dengan penanda kolom merupakan
pendekatan rata-rata dari kelompok ke-k pada peubah ke-j yang telah terkoreksi terhadap rata-rata terboboti seluruh objek. Sehingga memungkinkan untuk karakterisasi perbedaan antarkelompok,
. (50)
3. Kualitas representasi (atau ukuran kesesuaian dari matriks data) dapat didekati oleh:
. (51)
4. Matriks sebagai pendekatan matriks JKK data dalam kelompok, yaitu:
5. Panjang penanda kolom sebanding dengan variabilitas dalam kelompok-kelompok, = , dengan = .
6. Kosinus sudut antarpeubah dapat diinterpretasikan sebagai pendekatan dari korelasinya.
Analisis Procrustes
Dalam Bakhtiar dan Siswadi (2011) analisis Procrustes adalah alat analisis berdasarkan asas kuadrat terkecil yang dapat digunakan untuk mengukur kemiripan maksimal antarkonfigurasi titik melalui serangkaian transformasi linear. Analisis ini bertujuan untuk membandingkan dua konfigurasi yang mewakili unit pengamatan yang sama. Untuk melihat kesamaan bentuk dan ukuran dari dua konfigurasi maka setelah kedua konfigurasi dilakukan translasi salah satu konfigurasi dibuat tetap sementara konfigurasi yang lainnya ditransformasikan sehingga paling sesuai dengan konfigurasi pertama.
Misalnya adalah konfigurasi titik dalam ruang Euclid berdimensi dengan koordinat diberikan oleh matriks berikut
, (53)
dengan , untuk dan konfigurasi yang merupakan konfigurasi titik dalam ruang Euclid berdimensi . Konfigurasi
Dalam menentukan tingkat kesesuaian dua konfigurasi, analisis Procrustes mendasarkan penghitungannya pada jumlah kuadrat jarak antartitik yang bersesuaian, disebut juga jarak Procrustes, yaitu
. (54)
Dengan mempertimbangkan perubahan posisi, orientasi, dan skala dua konfigurasi yang dibandingkan, analisis Procrustes mensyaratkan tiga bentuk transformasi geometris harus dilakukan untuk mendapatkan E yang optimal. Ketiga bentuk transformasi ini adalah translasi, rotasi dan dilasi.
Translasi
Translasi dalam analisis Procrustes merupakan proses penggeseran semua titik pada konfigurasi dan konfigurasi dengan jarak yang tetap dan arah yang sama sehingga kedua konfigurasi memiliki sentroid (titik berat) yang sama.
Penguraian jumlah kuadrat persamaan (54) menghasilkan
. (55)
Karena bentuk kedua dari ruas kanan persamaan (55) bernilai nol, maka diperoleh
, (56)
di mana
1 , 1 ,
,
Penyesuaian optimal dengan translasi diperoleh dengan menghimpitkan sentroid X dan Y ( . Jadi, norma kuadrat perbedaan minimum dua konfigurasi setelah penyesuaian dengan translasi adalah:
(57)
Rotasi
Rotasi adalah proses pemindahan seluruh titik dengan sudut yang tetap tanpa mengubah jarak setiap titik terhadap sentroidnya. Dalam analisis Procrustes rotasi dilakukan dengan cara menggandakan konfigurasi dengan matriks ortogonal yang meminimumkan jarak antarkonfigurasi.
Norma kuadrat perbedaan kedua konfigurasi setelah penyesuaian dengan rotasi adalah
Q
Inf . (58)
Secara aljabar, berdasarkan (54) diperoleh:
. (59) Untuk memperoleh nilai yang minimum harus dipilih matriks ortogonal Q yang memaksimumkan nilai .
Misalnya merupakan hasil penguraian nilai singular bentuk lengkap dari matriks , sehingga , dengan adalah matriks diagonal dan merupakan matriks ortogonal, maka
, (60)
. (61)
Jadi, E minimum ketika , mengakibatkan
, (62)
atau
. (63)
Jadi, jarak Procrustes oleh rotasi yang optimal diberikan oleh:
. (64)
Dilasi
Dilasi adalah pembesaran/pengecilan jarak setiap titik dalam konfigurasi terhadap sentroidnya. Dilasi Y terhadap X dilakukan dengan menggandakan konfigurasi Y dengan suatu skalar c. Norma kuadrat perbedaan kedua konfigurasi setelah penyesuaian dengan dilasi adalah
c
Inf . (65)
sehingga
. (66) yang dapat dilihat sebagai fungsi kuadrat dalam c, sehingga nilai minimum diperoleh dengan memilih
. (67)
Jadi, jarak Procrustes oleh dilasi yang optimal diberikan oleh:
Bakhtiar dan Siswadi (2011) telah menunjukkan bahwa urutan optimal transformasi linear dalam analisis Procrustes ialah translasi, rotasi dan dilasi, dengan jarak Procrustes diberikan oleh:
Untuk memperoleh posisi yang paling sesuai sehingga kedua matriks menjadi semakin dekat dilakukan penyesuaian seperti di atas. Ukuran kesesuaian dua konfigurasi menggambarkan kedekatan (kesesuaian) antara dua matriks. Semakin tinggi nilainya, maka kedua konfigurasi tersebut akan semakin dekat (sama). Ukuran kesesuaian dapat dirumuskan sebagai:
METODE PENELITIAN
Sumber Data
Data yang digunakan dalam penelitian ini adalah data sekunder terdiri dari 3047 mahasiswa yang berasal dari 32 provinsi (1 provinsi tidak ada mahasiswa TPB IPB yang mewakilinya, yaitu Sulawesi Tengah) asal sekolah menengahnya serta data nilai mutu mata kuliah dan IPK mahasiswa TPB IPB tahun akademik 2009/2010 yang diperoleh dari Direktorat Pendidikan Tingkat Persiapan Bersama Institut Pertanian Bogor (TPB IPB).
Objek dalam penelitian ini adalah mahasiswa dengan provinsi asal sekolah menengahnya dan sebagai peubahnya adalah nilai mutu 14 mata kuliah dan IPK. Jadi, diperoleh matriks data peubah ganda berukuran 3047×15 yang menunjukkan 3047 mahasiswa dengan 15 peubah yang diamati dan matriks data asal yang telah ditransformasi sehingga berukuran 32×15 yang menunjukkan 32 provinsi asal sekolah menengah mahasiswa dengan 15 peubah yang diamati.
Peubah Penelitian
Peubah yang digunakan dalam penelitian ini merupakan mata kuliah dan IPK selama di TPB IPB yang disajikan pada Tabel 2.
Tabel 2 Peubah penelitian
No. Peubah Kode
1 Agama AG
2 Pendidikan Kewarganegaraan KN
3 Bahasa Indonesia ID
4 Pengantar Ilmu Pertanian PP
5 Bahasa Inggris IG
6 Olahraga dan Seni OS
7 Pengantar Matematika PM
8 Kalkulus KA
9 Kimia KI
10 Biologi BI
11 Fisika FI
12 Ekonomi Umum EK
13 Sosiologi Umum SU
Nilai mutu yang digunakan dalam konversi huruf mutu yang berlaku di IPB disajikan pada Tabel 3.
Tabel 3 Konversi huruf mutu No Huruf Mutu Nilai Mutu
1 A 4.00
2 B 3.00
3 C 2.00
4 D 1.00
5 E 0.00
Objek Penelitian
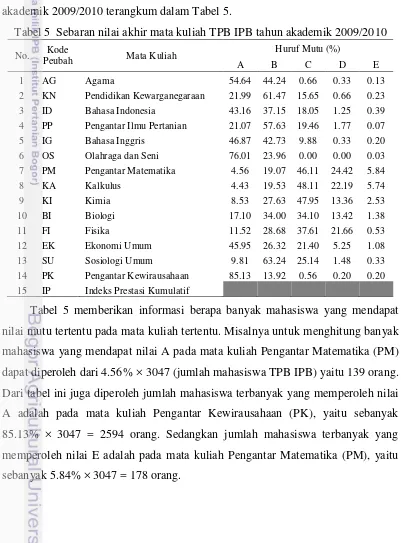
Objek penelitian adalah mahasiswa dengan provinsi asal sekolah menengahnya, terwakili oleh mahasiswa TPB IPB tahun akademik 2009/2010 yang berjumlah 3047 mahasiswa dari 32 provinsi. Provinsi asal mahasiswa dan banyak mahasiswa yang mewakilinya disajikan dalam Tabel 4.
Tabel 4 Provinsi asal mahasiswa dan banyak mahasiswa yang mewakilinya Asal Provinsi Kode Banyak
Mahasiswa Asal Provinsi Kode
Banyak Mahasiswa
Aceh 1 32 Bali 17 17
Sumatera Utara 2 162 Nusa Tenggara Barat 18 18 Sumatera Barat 3 109 Nusa Tenggara Timur 19 6
Riau 4 47 Kalimantan Barat 20 20
Jambi 5 26 Kalimantan Tengah 21 8
Sumatera Selatan 6 41 Kalimantan Selatan 22 5
Bengkulu 7 19 Kalimantan Timur 23 13
Lampung 8 83 Sulawesi Utara 24 2
Kepulauan Bangka Belitung 9 15 Sulawesi Selatan 25 23
Kepulauan Riau 10 7 Sulawesi Tenggara 26 8
DKI Jakarta 11 482 Sulawesi Barat 27 6
Jawa Barat 12 1183 Gorontalo 28 5
Banten 13 163 Maluku 29 1
Jawa Tengah 14 255 Maluku Utara 30 16
Daerah Istimewa Yogyakarta 15 8 Papua Barat 31 12
Metode Penelitian
Langkah-langkah dalam penelitian ini ialah:
1. Mengimplementasikan ukuran kesesuaian dua konfigurasi matriks dengan analisis Procrustes dan biplot kanonik dengan pemrograman fungsional Mathematica.
2. Eksplorasi data dilakukan dengan menggunakan : a. Sebaran nilai mata kuliah.
b. Diagram kotak garis dengan Minitab 15. c. Korelasi Pearson dengan Minitab 15. d. Peringkat dengan Excel.
e. Seleksi peubah dengan analisis komponen utama (AKU).
Tahapan dalam proses seleksi peubah menggunakan AKU, dalam penelitian ini berbasis matriks koragam, yaitu memperoleh eigennilai dan eigenvektor dari matriks koragam menggunakan Minitab 15 dan hasilnya dapat dilihat pada Lampiran 6. Kemudian pengurangan peubah dimulai dari komponen utama terakhir dengan melihat elemen eigenvektor yang memiliki nilai mutlak terbesar. Pengurangan peubah dilakukan kembali sampai dengan jumlah peubah yang dipertahankan diperoleh. Ada peneliti yang menggunakan petunjuk praktis untuk menggunakan k komponen
utama pertama bila keragaman yang dapat dijelaskan ≥ 80%.
3. Analisis data
agregasi
transformasi transformasi a. Biplot biasa
b. Biplot Kanonik
4. Menelusuri ketepatan biplot biasa dengan menggunakan ukuran kesesuaian dari Gabriel (2002).
5. Menentukan kesesuaian konfigurasi matriks data asal dengan matriks koordinat biplot serta antara matriks koordinat biplot biasa dan kanonik menggunakan analisis Procrustes.
6. Melakukan perbandingan analisis biplot biasa dengan biplot kanonik dari analisis yang diperoleh.
HASIL DAN PEMBAHASAN
Implementasi Biplot Kanonik dan Analisis Procrustes dengan Mathematica
Biplot biasa dengan sistem perintah telah terintegrasi ke dalam beberapa program paket statistika seperti SAS, R dan Stata. Sejalan dengan makin berkembangnya teknik komputasi dengan sistem aljabar komputer (SAK), biplot biasa telah diimplementasikan ke dalam SAK Mathematica dengan pemrograman fungsional Mathematica berbasis GUI (Graphical User Interface) (Ardana dan Siswadi, 2009). Tetapi, implementasi biplot kanonik dan ukuran kesesuaian dua konfigurasi menggunakan analisis Procrustes dengan sistem perintah belum terintegrasi dalam suatu program paket statistika. Oleh karena itu dalam penelitian ini paket program tersebut akan disusun menggunakan softwareMathematica 8.0.
Analisis biplot kanonik merupakan representasi grafik dari analisis peubah kanonik, dikembangkan oleh Gabriel (1995) untuk memperoleh representasi secara serempak antara rata-rata kelompok dan peubah.
Algoritma untuk memperoleh analisis biplot kanonik ialah:
1. Misalnya adalah matriks data asal berukuran dan adalah matriks indikator m kelompok berukuran .
2. Menentukan matriks data asal yang terkoreksi terhadap nilai rata-rata kolomnya dengan rumus 11' .
3. Menentukan matriks rata-rata kelompok, yaitu dengan .
4. Menentukan matriks jumlah kuadrat dan hasil kali data dalam kelompok dengan rumus .
5. Menentukan matriks rata-rata kelompok terboboti, yaitu . 6. Menggunakan penguraian nilai singular terhadap matriks , sehingga
diperoleh .
8. Koordinat rata-rata kelompok dan peubah yang diperoleh kemudian diplot menggunakan paket BiplotGH Ver. 1.0 (Ardana, 2009).
Hasil yang diperoleh dari program di atas berupa suatu perintah/fungsi
BiplotKanonik [X,Z], dengan argumen X adalah matriks data dengan n objek dan p peubah dan argumen Z adalah matriks indikator. Perintah di atas menghasilkan matriks objek (G), matriks peubah (H), Hlabel, ukuran dimensi 1, ukuran dimensi 2 dan ukuran kesesuaian biplot kanonik (GF). Kemudian plot menggunakan perintah BiplotGH[G,H,options], dengan argumen G adalah matriks objek, argumen H adalah matriks peubah dan argumen options berupa tambahan untuk label titik-titik objek dan vektor peubah serta semua opsi grafik. Namun sebelumnya tuliskan perintah <<BiplotKanonik` dan <<BiplotGH` untuk menemukan file agar dapat terbaca.
Ukuran kesesuaian matriks data, objek dan peubah dalam analisis biplot biasa dan kanonik serta ukuran kesesuaian antara koordinat biplot biasa dan kanonik dapat diperoleh dengan menggunakan nilai norma kuadrat perbedaan minimum dalam analisis Procrustes. Hal ini telah ditunjukkan oleh Bakhtiar dan Siswadi (2011) bahwa urutan optimal transformasi linear dalam analisis Procrustes ialah translasi, rotasi dan dilasi.
Algoritma untuk menghitung ukuran kesesuaian dengan analisis Procrustes : 1. Misalnya dan adalah dua konfigurasi matriks berukuran .
2. Menentukan konfigurasi dan setelah ditranslasi, yaitu dan dengan rumus 1 dan 1 , di mana 1 dan 1
merupakan sentroid kolom dari konfigurasi dan .
3. Menentukan matriks ortogonal untuk transformasi rotasi, dengan matriks dan merupakan hasil penguraian nilai singular bentuk lengkap dari matriks menjadi .
4. Menghitung skalar
untuk transformasi dilasi.
5. Menghitung nilai norma kuadrat perbedaan kedua konfigurasi setelah penyesuaian dengan translasi, rotasi dan dilasi, yaitu
6. Menghitung ukuran kesesuaian dua konfigurasi, yaitu
.
Hasil utama yang diperoleh dari program di atas berupa suatu perintah/fungsi GFProcrustes[X,Y]. Argumen X adalah matriks konfigurasi pertama dan argumen Y adalah matriks konfigurasi kedua. Namun sebelumnya tuliskan perintah <<GFProcrustes` untuk menemukan file agar dapat terbaca.
Eksplorasi Data
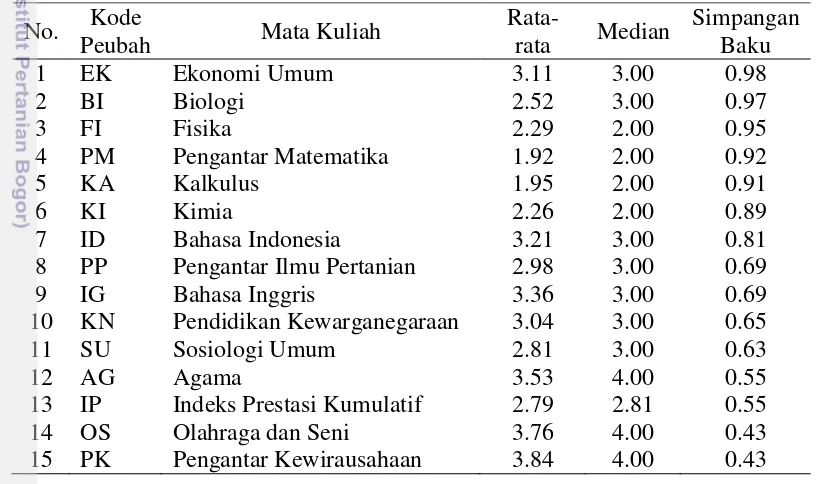
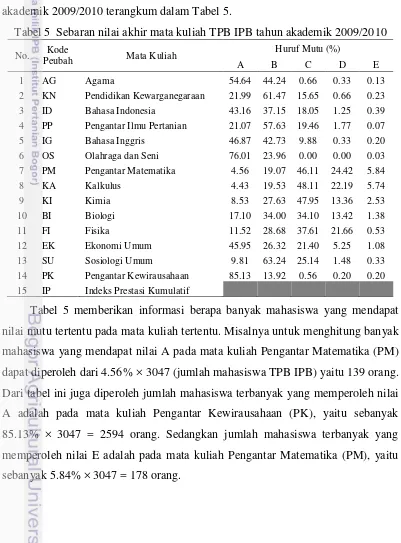
Sebaran nilai akhir mata kuliah yang diikuti mahasiswa TPB IPB tahun akademik 2009/2010 terangkum dalam Tabel 5.
Tabel 5 Sebaran nilai akhir mata kuliah TPB IPB tahun akademik 2009/2010 No. Kode
Peubah Mata Kuliah
Huruf Mutu (%)
A B C D E
1 AG Agama 54.64 44.24 0.66 0.33 0.13
2 KN Pendidikan Kewarganegaraan 21.99 61.47 15.65 0.66 0.23 3 ID Bahasa Indonesia 43.16 37.15 18.05 1.25 0.39 4 PP Pengantar Ilmu Pertanian 21.07 57.63 19.46 1.77 0.07 5 IG Bahasa Inggris 46.87 42.73 9.88 0.33 0.20 6 OS Olahraga dan Seni 76.01 23.96 0.00 0.00 0.03 7 PM Pengantar Matematika 4.56 19.07 46.11 24.42 5.84 8 KA Kalkulus 4.43 19.53 48.11 22.19 5.74
9 KI Kimia 8.53 27.63 47.95 13.36 2.53
10 BI Biologi 17.10 34.00 34.10 13.42 1.38 11 FI Fisika 11.52 28.68 37.61 21.66 0.53 12 EK Ekonomi Umum 45.95 26.32 21.40 5.25 1.08 13 SU Sosiologi Umum 9.81 63.24 25.14 1.48 0.33 14 PK Pengantar Kewirausahaan 85.13 13.92 0.56 0.20 0.20 15 IP Indeks Prestasi Kumulatif
Ukuran pemusatan dan penyebaran nilai mata kuliah dan IPK mahasiswa TPB IPB tahun akademik 2009/2010 ditata berdasarkan simpangan baku diberikan dalam Tabel 6. Tabel 6 dapat memberikan informasi tentang kontribusi nilai mata kuliah terhadap perolehan IPK. Kontribusi terbesar berasal dari mata kuliah Pengantar Kewirausahaan (PK) dengan rata-rata 3.84, Olahraga dan Seni (OS) dengan rata-rata 3.76, Agama (AG) dengan rata-rata 3.53, Bahasa Inggris (IG) dengan rata-rata 3.36 dan Bahasa Indonesia (ID) dengan rata-rata 3.21. Sedangkan mata kuliah yang memberikan kontribusi tidak terlalu besar terhadap IPK yaitu mata kuliah Pengantar Matematika (PM) dengan rata-rata 1.92, Kalkulus (KA) dengan rata-rata 1.95, Kimia (KI) dengan rata-rata 2.26 dan Fisika (FI) dengan rata-rata 2.29.
Tabel 6 Ukuran pemusatan dan penyebaran nilai mata kuliah dan IPK mahasiswa TPB IPB tahun akademik 2009/2010
Tabel 6 juga dapat memberikan informasi tentang keragaman peubah (nilai mata kuliah). Mata kuliah Ekonomi Umum (EK), Biologi (BI), Fisika (FI), Pengantar Matematika (PM), Kalkulus (KA) dan Kimia (KI) memiliki nilai lebih beragam daripada mata kuliah lainnya. Sedangkan mata kuliah Agama (AG), Olahraga dan Seni (OS), Pengantar Kewirausahaan (PK) dan Indeks Prestasi Kumulatif (IP) memiliki keragaman nilai yang relatif kecil.
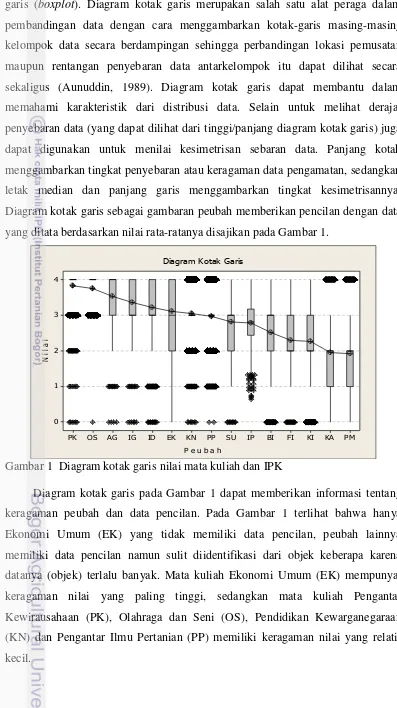
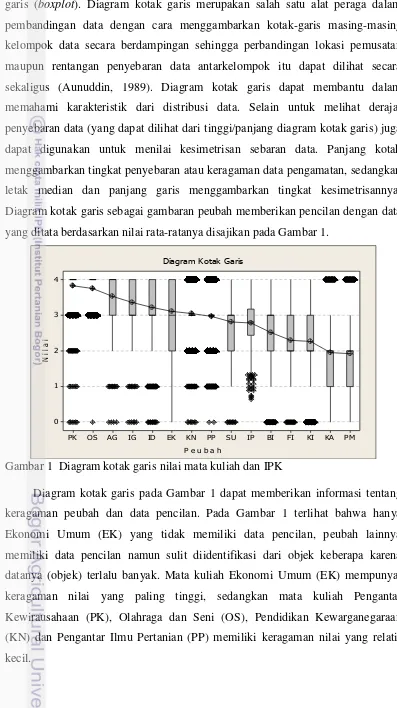
garis (boxplot). Diagram kotak garis merupakan salah satu alat peraga dalam pembandingan data dengan cara menggambarkan kotak-garis masing-masing kelompok data secara berdampingan sehingga perbandingan lokasi pemusatan maupun rentangan penyebaran data antarkelompok itu dapat dilihat secara sekaligus (Aunuddin, 1989). Diagram kotak garis dapat membantu dalam memahami karakteristik dari distribusi data. Selain untuk melihat derajat penyebaran data (yang dapat dilihat dari tinggi/panjang diagram kotak garis) juga dapat digunakan untuk menilai kesimetrisan sebaran data. Panjang kotak menggambarkan tingkat penyebaran atau keragaman data pengamatan, sedangkan letak median dan panjang garis menggambarkan tingkat kesimetrisannya. Diagram kotak garis sebagai gambaran peubah memberikan pencilan dengan data yang ditata berdasarkan nilai rata-ratanya disajikan pada Gambar 1.
PM
Gambar 1 Diagram kotak garis nilai mata kuliah dan IPK
Posisi median di dalam diagram kotak garis akan menunjukkan kemiringan pola sebaran data. Peubah Pendidikan Kewarganegaraan (KN), Pengantar Ilmu Pertanian (PP), Kalkulus (KA), Pengantar Matematika (PM) dan IPK (IP) kemiringan pola sebarannya mendekati simetri atau mediannya hampir sama dengan rata-ratanya. Peubah Pengantar Kewirausahaan (PK), Olahraga dan Seni (OS), Agama (AG), Sosiologi Umum (SU) dan Biologi (BI) mempunyai kemiringan pola sebaran datanya negatif, hal ini menunjukkan bahwa rata-rata kelima peubah tersebut lebih kecil dari mediannya, sedangkan peubah Bahasa Inggris (IG), Bahasa Indonesia (ID), Ekonomi Umum (EK), Fisika (FI) dan Kimia (KI) mempunyai kemiringan pola sebaran datanya positif, hal ini mengindikasikan bahwa rata-rata kelima peubah tersebut lebih besar dari mediannya.
Hubungan linear antara dua peubah atau lebih tidak dapat dibaca dari diagram kotak garis, maka digunakan korelasi Pearson seperti yang diberikan pada Tabel 7 untuk menyatakan ada atau tidaknya hubungan antarpeubah dan untuk menyatakan besarnya sumbangan peubah satu terhadap peubah lainnya. Signifikansi korelasi pada Tabel 7 berdasarkan nilai-p hampir semuanya kurang dari 1%, ini menunjukkan korelasinya sangat nyata. Korelasi dengan nilai-p-nya disajikan pada Lampiran 5.
Tabel 7 Matriks korelasi Pearson data asal
AG KN ID PP IG OS PM KA KI BI FI EK SU PK IP
berkorelasi dengan peubah Biologi (BI), Kimia (KI), Pengantar Matematika (PM)
dan peubah Kalkulus (KA) dengan nilai korelasi ≥ 0.80**. Ini menunjukkan bahwa rata-rata IPK yang dicapai mahasiswa sangat dipengaruhi oleh nilai mata kuliah Biologi, Kimia, Pengantar Matematika dan Kalkulus. Sedangkan dengan peubah Pengantar Kewirausahaan (PK) dan Olahraga dan Seni (OS), peubah IPK (IP) berkorelsi sangat rendah dengan nilai korelasi ≤ 0.20**. Hal ini menunjukkan bahwa nilai mata kuliah Pengantar Kewirausahaan serta Olahraga dan Seni kecil pengaruhnya terhadap nilai IPK. Secara umum, hampir semua korelasi antarpeubah sangat nyata, walaupun nilainya tidak begitu besar, kecuali peubah Olahraga dan Seni (OS) tidak berkorelasi dengan peubah Bahasa Indonesia (ID) dan Bahasa Inggris (IG).
Gambaran Umum Provinsi
Gambaran umum mutu pendidikan tiap provinsi dapat dilihat pada pencapaian prestasi mahasiswanya di IPB dalam bidang akademik yang umumnya dilihat dari indikator nilai IPK. IPK merupakan nilai kumulatif dari 14 mata kuliah yang diikuti mahasiswa TPB IPB. Walaupun mahasiswa yang mewakili provinsinya berjumlah tidak merata, akan tetapi nilai yang digunakan adalah nilai rata-rata per provinsi. Jika rata-rata nilai IPK mahasiswa dari suatu provinsi lebih tinggi maka provinsi tersebut mempunyai mutu pendidikan lebih baik dengan provinsi lainnya. Peringkat provinsi berdasarkan rata-rata IPK disajikan pada Gambar 2.
Gambar 2 Peringkat provinsi berdasarkan rata-rata IPK
Seleksi Peubah
Sebagai penyederhanaan dan meningkatkan ketepatan model pada analisis maka dilakukan proses seleksi peubah yaitu proses pengidentifikasian dan pengurangan peubah-peubah yang memberikan kontribusi informasi yang relatif kecil pada keragaman data. Alasan seleksi peubah untuk merepresentasikan keragaman total pada keseluruhan data dapat berdasarkan pada pertimbangan bahwa beberapa peubah mungkin sulit ataupun mahal untuk diukur pada studi berikutnya, atau meskipun peubah tersebut biasanya dapat diinterpretasikan, komponen utama yang telah ditentukan dapat menjadi sulit diinterpretasikan jika terlalu banyak peubah yang terlibat.
Seleksi peubah dalam penelitian ini dilakukan melalui teknik analisis komponen utama (AKU, Principal Component Analysis). AKU biasanya digunakan untuk: (1) identifikasi peubah baru yang mendasari data peubah ganda, (2) mengurangi banyaknya dimensi himpunan peubah yang biasanya terdiri atas peubah yang banyak dan saling berkorelasi menjadi peubah-peubah baru yang tidak berkorelasi dengan mempertahankan sebanyak mungkin keragaman dalam
1.61, n29 = 1
0.00 0.50 1.00 1.50 2.00 2.50 3.00 3.50 4.00
himpunan data tersebut, dan (3) menghilangkan peubah-peubah asal yang mempunyai sumbangan informasi yang relatif kecil (Siswadi dan Suharjo, 1999).
Peubah baru yang dimaksud di atas disebut komponen utama yang berciri: (1) merupakan kombinasi linear peubah-peubah asal, (2) jumlah kuadrat koefisien dalam kombinasi linear tersebut bernilai satu, (3) tidak berkorelasi, dan (4) mempunyai ragam berurut dari yang terbesar ke yang terkecil.
Peubah-peubah yang terseleksi menggunakan teknik AKU adalah peubah IPK (IP), Pendidikan Kewirausahaan (PK), Olahraga dan Seni (OS), Kalkulus (KA), Agama (AG), Sosiologi Umum (SU) dan Kimia (KI). Berdasarkan Tabel 6 peubah IPK (IP), Pendidikan Kewirausahaan (PK), Olahraga dan Seni (OS), Agama (AG) dan Sosiologi Umum (SU) memiliki keragaman yang relatif kecil. Berdasarkan Tabel 7 peubah Kalkulus (KA) mempunyai korelasi Pearson yang relatif besar dengan peubah Pengantar Matematika (PM), yaitu 0.74** sehingga peubah Kalkulus (KA) terwakili oleh peubah Pengantar Matematika (PM), sedangkan peubah Kimia (KI) mempunyai korelasi Pearson yang relatif besar dengan peubah Biologi (BI), yaitu 0.66** sehingga peubah Kimia (KI) terwakili oleh peubah Biologi (BI). Jadi, peubah-peubah yang dipertahankan dan digunakan dalam analisis berikutnya adalah peubah Pendidikan Kewarganegaraan (KN), Bahasa Indonesia (ID), Pengantar Ilmu Pertanian (PP), Bahasa Inggris (IG), Pengantar Matematika (PM), Biologi (BI), Fisika (FI) dan Ekonomi Umum (EK) yang dapat menjelaskan keragaman data asal sebesar 85.40%. Pengukuran efisiensi atau kesesuaian matriks data setelah seleksi peubah dengan matriks data asal menggunakan analisis Procrustes menghasilkan ukuran efisiensi yang cukup besar, yaitu 98.89%.
Analisis Biplot Biasa dan Kanonik Data Asal
Gambar 3 Biplot biasa pada data asal
Gambar 4 Biplot kanonik pada data asal
Secara umum interpretasi biplot biasa dan kanonik mempunyai persamaan dan perbedaan, hal ini dapat dilihat baik dari kedekatan antarobjek (provinsi),
0.04 0.02 0.00 0.02 0.04 0.06 0.08
0.03
0.06 0.04 0.02 0.00 0.02 0.04 0.06