PENGARUH PENDEKATAN MATEMATIKA REALISTIK
TERHADAP KEMAMPUAN PENALARAN DAN
PEMECAHAN MASALAH MATEMATIKA
SISWA SMA
Tesis
Diajukan untuk Memenuhi Persyaratan dalam Memperoleh Gelar Magister Pendidikan pada
Program Studi Pendidikan Matematika
Oleh :
ADISAPUTRA NIM. 8096171001
PROGRAM PASCASARJANA
UNIVERSITAS NEGERI MEDAN
ABSTRAK
ADISAPUTRA. Pengaruh Pendekatan Matematika Realistik Terhadap Kemampuan
Penalaran dan Pemecahan Masalah Matematika Siswa SMA Tesis. Medan. 2014. Program Studi Pendidikan Matematika, Pasca Sarjana, Universitas Negeri Medan
Kata Kunci: Pendekatan Matematika Realistik, Kemampuan Penalaran Matematika dan Pemecahan Masalah Matematik.
ii ABSTRACT
ADISAPUTRA. Influence Realistic Mathematics Education Reasoning Ability and
Mathematical Problem Solving High School Students Thesis. Medan. 2014. Mathematics Education Study Program, Graduate School, University of Medan. Keywords: Realistic Mathematics Education, Mathematical Reasoning Ability and Mathematical Problem Solving.
KATA PENGANTAR
Alhamdulillahirrabil’ alamin, segala puji dan syukur hanya kepada Allah
SWT Yang Maha Sempurna dan Mengetahui segalahnya. Atas limpahan rahmat dan
karunia-Nya sehingga tesis yang berjudul : “Pengaruh Pendekatan Matematika
Realistik Terhadap Kemampuan Penalaran dan Pemecahan masalah
matematika Siswa SMA ” dapat penulis selesaikan dengan segala kekurangan dan
keterbatasan. Penulis menyadari bahwa tanpa bantuan, bimbingan dan motivasi dari
berbagai pihak, segala kekurangan dan keterbatasan penyusunan tesis ini tidak akan
teratasi dengan baik oleh karena itu, dalam kesempatan ini penulis menyampaikan
ucapan terima kasih yang tulus dan penghargaan yang setinggi-tinggihnya kepada
mereka yang telah berjasa, yaitu kepada:
1. Bapak Prof. Dian Armanto, M.Pd.,MA.,M.Sc.,Ph.D, selaku pembimbing I
yang penuh dengan kesabaran telah berkenan memberikan bimbingan dan
masukan kepada penulis dari proses awal penulisan hingga selesai. Dengan sifat
yang kritis telah berhasil membentuk wawasan berpikir penulis dalam
menyikapi dan mangatasi berbagai permasalahan.
2. Bapak Prof. Dr. Sumarno, M.Pd, selaku pembimbing II dengan kharisma dan
sifat kebijaksanaan serta kesabarannya senantiasa meluangkan waktu untuk
membimbing dan memotivasi serta nasehatnya yang menyejukan pada awal
penyusunan tesis ini, dapat mengurangi beban psikologis penulis dan berkenan
iv
3. Kepada saudara-saudaraku seangkatan di program S-2 pendidikan matematika
PPs UNIMED yang telah berjasa dan banyak membantu penulis selama masa
penulisan.
4. Kepada Bapak kepala SMA Negeri 1 Gebang Kabupaten Langkat beserta
guru-guru matematika pada sekolah tersebut yang selama pelaksanaan penelitian
menunjukan kerja sama yang harmonis dan saling menunjang terutama dalam
memberikan penilaian dan pertimbangan instrumen tes hasil belajar dalam
rangka keberhasilan penelitian ini.
5. Kepada Istri serta anak saya yang sekarang sedang kuliah, penulis ucapkan
terima kasih yang sedalam-dalamnya atas semua kasih sayang dan doa yang
telah diberikan kepada penulis agar senantiasa tabah, sabar dan semangat dalam
menyelesaikan penelitian ini.
6. Kepada abang dan adik, penulis ucapkan terima kasih yang sedalam-dalamnya
atas semua kasih sayang dan doa yang telah diberikan kepada penulis agar
senantiasa tabah, sabar dan semangat dalam menyelesaikan penelitian ini.
Semoga Allah yang maha Pengasih lagi Maha Penyayang, senantiasa
melimpahkan rahmat dan hidayahNya kepada semua pihak yang telah disebutkan di
atas yang telah berjasa membantu penulis dalam meraih cita-citanya yang mulia ini.
Amin Ya Robbal Alamin
Medan, Februari 2015 Penulis
DAFTAR ISI
Halaman
ABSTRAK ... i
ABSTRACT ... ii
KATA PENGANTAR ... iii
DAFTAR ISI ….………... v
DAFTAR TABEL... xi
DAFTAR GAMBAR... xv
DAFTAR LAMPIRAN ... xviii
BAB I PENDAHULUAN ... 1
1.1. Latar Belakang ... 1
1.2. Identifikasi Masalah ... 15
1.3. Pembatasan Masalah... 15
1.4. Rumusan Masalah ... 16
1.5. Tujuan Penelitian ... 17
1.6. Manfaat Penelitian ... 17
BAB II KAJIAN PUSTAKA... 20
2.1. Kerangka Teoritis... 20
2.1.1. Kemampuan Penalaran Matematika ... 20
2.1.2. Kemampuan Pemecahan Masalah Matematika ... 28
2.1.3. Hakekat Belajar dan Pembelajaran ... 34
2.1.4. Hakekat Matematika dan Belajar Matematika ... 38
2.1.5. Pendekatan Matematika Realistik ... 42
2.1.6. Pembelajaran Konvensional... 56
2.1.7. Sikap Siswa terhadap Matematika... 60
vi
2.1.9. Penelitian yang Relevan ………. 66
2.2. Kerangka Konseptual dan Hipotesis………... 68
2.2.1. Kerangka Konseptual ... 68
2.2.2. Hipotesis Penelitian ……… 77
BAB III METODE PENELITIAN……… 78
3.1. Tempat dan waktu Penelitian... 78
3.2. Populasi, Sampel dan Teknik Pengambilan Sampel ………... 78
3.2.1. Populasi Penelitian……….. 78
3.2.2. Sampel dan Teknik Pengambilan Sampel ………... 78
3.3. Desain Penelitian………... 79
3.4. Definisi Operasional ……… 82
3.5. Variabel Penelitian ………. 83
3.6. Teknik Pengumpulan Data…... ……… 84
3.6.1. Tes Kemampuan Penalaran Matematika ………. 84
3.6.2. Tes Kemampuan Pemecahan Masalah Matematika ..……. 86
3.6.3. Lembar Angket (kuisioner) Skala Sikap Siswa terhadap Matematika ………. 88
3.6.4. Lembar Observasi Aktivitas Guru ……….. 90
3.6.5. Lembar Observasi Aktivitas Siswa ……… 90
3.7. Uji Coba Instrumen ……… 90
3.8. Prosedur Penelitian ……… 99
3.9. Teknik Analisis Data ………101
BAB IV HASIL PENELITIAN DAN PEMBAHASAN... 107
4.1. Hasil Penelitian ... 107
4.1.1.1. Deskripsi Data Kemampuan Penalaran Matematika Matematika Realistik (PMR) Secara Keseluruhan ... 109
viii
4.1.1.9. Deskripsi Data Kemampuan Penalaran Matematika Siswa yang Diberikan pembelajaran Konvensional dan Sikap Siswa Terhadap Matematika Rendah... 119
4.1.1.10.Deskripsi Data Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Matematika Realistik (PMR) dan
Konvensional Secara Keseluruhan Yang Memiliki Sikap Siswa Terhadap Matematika Tinggi dan Sikap Siswa Terhadap Matematika Rendah... 120
4.1.1.11.Deskripsi Data Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Matematika Realistik (PMR) Secara
Keseluruhan... 123
4.1.1.12.Deskripsi Data Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional Secara Keseluruhan... 125
4.1.1.13.Deskripsi Data Kemampuan Pemecahan Masalah
Matematika Siswa yang Memiliki Sikap Siswa Terhadap Matematika Tinggi Secara Keseluruhan Baik yang Dibelajarkan Dengan Pendekatan
Matematika Realistik dan Konvensional... 126
4.1.1.14.Deskripsi Data Kemampuan Pemecahan Masalah
Matematika Siswa yang Memiliki Sikap Siswa
Terhadap Matematika Rendah Secara Keseluruhan Baik yang Dibelajarkan Dengan Pendekatan
Matematika Realistik dan Konvensional... 128
4.1.1.15.Deskripsi Data Kemampuan Pemecahan Masalah
Matematika Siswa yang Dibelajarkan Dengan Pendekatan Matematika Realistik dan Sikap Siswa Terhadap Matematika Tinggi... 130
Pendekatan Matematika Realistik dan Sikap Siswa
Terhadap Matematika Rendah... 132
4.1.1.17.Deskripsi Data Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional dan Sikap Siswa Terhadap Matematika Tinggi... 133
4.1.1.18.Deskripsi Data Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional dan Sikap Siswa Terhadap Matematika Rendah... 135
4.1.2. Pengujian Persyaratan Analisis... 136
4.1.2.1. Kemampuan Penalaran Matematika... 136
4.1.2.2. Kemampuan Pemecahan Masalah Matematika... 138
4.1.3. Pengujian Hipotesis... 140
4.1.3.1. Uji – t Data Skor Kemampuan Penalaran Matematika yang Diberikan Pembelajaran Dengan Pendekatan Matematika Realistik dan Konvensional... 141
4.1.3.2. Uji –t Data Skor Kemampuan Pemecahan Masalah Matematika yang Diberikan Pembelajaran dengan Pendekatan Matematika Rrealistik dan Konvensional... 142
4.1.3.3. Uji Anava interaksi antara pembelajaran dan sikap
4.2. Pembahasan Hasil Penelitian... 147
4.2.1. Faktor Pembelajaran... 147
4.2.2. Kemampuan Penalaran Matematika... 151
4.2.3. Kemampuan Pemecahan Masalah Matematika...154
x
4.3.Keterbatasan Penelitian... 147
BAB V SIMPULAN DAN SARAN ... 161
5.1. Simpulan ... 161.
5.2.Implikasi... 163
5.2. Saran ... 164
DAFTAR PUSTAKA ………... 167
DAFTAR TABEL
Halaman
Tabel 1.1. Data UH I dan II Matematika kls. X Semester Ganjil
T.P. 2012/2013 ... 10
Tabel 2.1. Sistaks Pendekatan Matematika Realistik... 52
Tabel 2.2. Implementasi PMR dalam Kegiatan Pembelajaran... 54
Tabel 2.3. Langkah-Langkah/ Sintaks Model Pembelajaran Konvensional…... 57
Tabel 2.4. Perbedaan Pedagogik antara Pendekatan Matematika Realistik denganPembelajaran Konvensional... 58
Tabel 3.1. Tabel Weiner tentang Keterkaitan antara Variabel Bebas, Variabel Terikat danVariabel Kontrol (Sikap Siswa)... 81
Tabel 3.2. Kisi-kisi Tes Kemampuan Penalaran Matematika ... 85
Tabel 3.3. Rubrik Pemberian Skor Tes Penalaran Matematika... 85
Tabel 3.4. Kisi-kisi Tes Kemampuan Pemecahan Masalah Matematika ... 87
Tabel 3.5. Pedoman Penskoran Kemampuan Pemecahan Masalah... 87
Tabel 3.6. Kisi-kisi Skala Sikap Siswa terhadap Matematika... 89
Tabel 3.7. Lima orang validator untuk memvalidasi seluruh perangkat pembelajaran dan lembar aktivitas siswa (LAS)... 91
Tabel 3.8. Hasil validasi ahli terhadap perangkat pembelajaran yaitu Rencana Pelaksanaan Pembelajaran (RPP) dan Lembar Aktivitas Siswa (LAS)... 91
Tabel 3.9. Validasi Butir Soal Hasil Uji Coba Tes Kemampuan Penalaran Matematika... 92
Tabel 3.10. Validasi Butir Soal Hasil Uji Coba Tes Kemampuan Pemecahan Matematika... 93
xii
Tabel 3.12. Tingkat Kesukaran Butir Soal Hasil Uji Coba Tes KemampuanPemecahan Masalah Matematika... 94
Tabel 3.13. Interpretasi Daya Pembeda Kemampuan Penalaran
Matematika... 95
Tabel 3.14. Interpretasi Daya Pembeda Kemampuan Pemecahan Masalah Matematika... 95
Tabel 3.15. Reliabilitas Hasil Uji Coba Kemampuan Penalaran
Matematika... 97
Tabel 3.16. Reliabilitas Hasil Uji Coba Kemampuan Pemecahan Masalah Matematika... 97
Tabel 3.17. Interpretasi Koefisien Reliabilitas... 98
Tabel 3.18. Keterkaitan Antara Rumusan Masalah, Hipotesis, Alat Ukur, dan Uji Statistik... 105 Tabel 4.1. Deskripsi Data Skor Kemampuan Penalaran dan
Pemecahan Masalah Matematika Siswa... 107
Tabel 4.2. Deskripsi Data Kemampuan Penalaran Matematika Siswa yang Dibelajarkan Dengan Pendekatan Matematika
Realistik (PMR) dan Konvensional Secara Keseluruhan
yang Memiliki Sikap Siswa Terhadap Matematika Tinggi dan Sikap Siswa Terhadap Matematika Rendah... 108
Tabel 4.3. Deskripsi Data Kemampuan Penalaran Matematika Siswa Pendekatan Matematika Realistik dan Konvensional ... 112
Tabel 4.6. Deskripsi Data Kemampuan Penalaran Matematika Siswa yang Memiliki Sikap Siswa Terhadap Matematika Rendah Secara Keseluruhan Baik yang Dibelajarkan Dengan Pendekatan Matematika Realistik dan Konvensional... 114
Tabel 4.8. Deskripsi Data Kemampuan Penalaran Matematika Siswa yang Dibelajarkan Dengan Pendekatan Matematika Realistik dan Sikap Siswa Terhadap Matematika Rendah... 117
Tabel 4.9. Deskripsi Data Kemampuan Penalaran Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional dan Sikap Siswa Terhadap Matematika Tinggi... 118
Tabel 4.10. Deskripsi Data Kemampuan Penalaran Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional dan Sikap Siswa Terhadap Matematika Rendah... 120
xiv
Tabel 4.18. Deskripsi Data Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional dan Sikap Siswa Terhadap
Matematika Tinggi... 134
Tabel 4.19. Deskripsi Data Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional dan Sikap Siswa Terhadap
Matematika Rendah... 135
Tabel 4.20. Rangkuman Analisis Uji Normalitas Kemampuan Penalaran Matematika... 137
Tabel 4.21. Rangkuman Analisis Uji Homogenitas Skor Kemampuan Penalaran Matematika... 138
Tabel 4.22. Rangkuman Analisis Uji Normalitas Kemampuan Pemecahan Masalah Matematika... 139
Tabel 4.23. Rangkuman Analisis Uji Homogenitas Skor Kemampuan Pemecahan Masalah Matematika... 140
Tabel 4.24. Hasil Uji –t Data Skor Kemampuan Penalaran Matematika yang Diberikan Pembelajaran dengan Pendekatan Matematika realistik dan konvensional... 142
Tabel 4.25. Hasil Uji –t Data Skor Kemampuan Pemecahan Masalah Matematika yang Diberikan Pembelajaran dengan Pendekatan matematika realistik dan konvensional... 143
Tabel 4.26 Interaksi antara Pembelajaran dan Sikap Siswa terhadap Kemampuan Penalaran Matematika Siswa. ... 144
Tabel 4.27. Interaksi antara Pembelajaran dan Sikap Siswa terhadap Kemampuan Pemecahan Masalah Matematika Siswa... 146
Tabel 4.28. Rangkuman Hasil Perhitungan Rata-rata Aspek Kemampuan penalaran matematika siswa... 146
DAFTAR GAMBAR
Halaman
Gambar 1.1. Sebuah Kubus ABCDEFGH... 5
Gambar 1.2. Penangkar burung berbentuk sebuah balok... 7
Gambar 2.1. Contoh analogi... 23
Gambar 2.2. Diagram Venn Sillogisma a…... 26
Gambar 2.3. Diagram Venn Sillogisma b... 26
Gambar 2.4. Diagram Venn silogisma... 27
Gambar 2.5. Konsep Matematisasi (De Lange dalam Sudharta, 2004). ... 46
Gambar 2.6 Langkah-langkah pembelajaran matematika dengan PMR... 50
Gambar 4.1. Histogram Kemampuan Penalaran Matematika Siswa yang Dibelajarkan Dengan Pendekatan Matematika Realistik (PMR) dan Konvensional Secara Keseluruhan yang Memiliki Sikap Siswa Terhadap Matematika Tinggi dan Sikap Siswa Terhadap Matematika Rendah...109
Gambar 4.2 Histogram Kemampuan Penalaran Matematika Siswa yang Dibelajarkan Dengan Pendekatan Matematika Realistik (PMR) Secara Keseluruhan...110
Gambar 4.3. Histogram Kemampuan Penalaran Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional... 112
Gambar 4.4. Histogram Kemampuan Penalaran Matematika Siswa yang Memiliki Sikap Siswa Terhadap Matematika Tinggi yang Dibelajarkan dengan Pendekatan Matematika Realistik dan Konvensional... 113
Gambar 4.5 Histogram Kemampuan Penalaran Matematika Siswa yang Memiliki Sikap Siswa Terhadap Matematika Rendah yang Dibelajarkan dengan Pendekatan Matematika Realistik dan Konvensional... 115
xvi
Gambar 4.7. Histogram Kemampuan Penalaran Matematika Siswa yang Dibelajarkan dengan Pendekatan Matematika Realistik dan Sikap Siswa Terhadap Matematika Rendah... 118
Gambar 4.8. Histogram Kemampuan Penalaran Matematika Siswa
yang Dibelajarkan Dengan Pendekatan Konvensional dan Sikap Siswa Terhadap Matematika Tinggi... 119
Gambar 4.9. Histogram Kemampuan Penalaran Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional dan Sikap Siswa Terhadap Matematika Rendah... 121
Gambar 4.10. Histogram Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Matematika Realistik (PMR) dan Konvensional Secara Keseluruhan yang Memiliki Sikap Siswa Terhadap Matematika Tinggi dan Sikap Siswa Terhadap Matematika Rendah... 123
Gambar 4.11 Histogram Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Matematika Realistik (PMR) Secara Keseluruhan 124
Gambar 4.12. Histogram Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pendekatan Konvensional... 126
Gambar 4.13. Histogram Kemampuan Pemecahan Masalah Matematika Siswa yang Memiliki Sikap Siswa Terhadap Matematika Tinggi yang Dibelajarkan dengan Pendekatan Matematika Realistik dan Konvensional... 128
Gambar 4.14. Histogram Kemampuan Pemecahan Masalah Matematika Siswa yang Memiliki Sikap Siswa Terhadap Matematika Rendah yang Dibelajarkan dengan Pendekatan Matematika Realistik dan Konvensional... 130
Gambar 4.15. Histogram Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan dengan Pendekatan Matematika Realistik dan Sikap Siswa Terhadap Matematika Tinggi... 131
Gambar 4.16 Histogram Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan dengan Pendekatan Matematika Realistik dan Sikap Siswa Terhadap Matematika Rendah... 133
Gambar 4.18. Histogram Kemampuan Pemecahan Masalah Matematika Siswa yang Dibelajarkan Dengan Pembelajaran Konvensional dan Sikap Siswa Terhadap Matematika Rendah... 136
Gambar 4.19. Interaksi antara pembelajaran dan sikap siswa terhadap kemampuan penalaran matematika siswa... 145
xviii
DAFTAR LAMPIRAN
Halaman
Lampiran 1. Silabus ... 171
Lampiran 2. RPP PMR ... 173
Lampiran 3. Lembar Aktivitas Siswa (LAS)... 209
Lampiran 4. Lembar Angket Sikap Siswa …... 234
Lampiran 5. Tes Penalaran Matematika... 237
Lampiran 6. Tes Pemecahan Masalah Matematika... 240
Lampiran 7. Kunci Tes Penalaran Matematika... 243
Lampiran 8. Kunci Tes Pemecahan Masalah... 245
Lampiran 9. Uji Validasi dan Reliabilitas... 250
Lampiran 10. Uji Validasi, Reliabilitas, Daya Beda dan Tingkat Kesukaran Tes Kemamapuan Penalaran Matematika Siswa...256
Lampiran 11 Uji Validasi, Reliabilitas, Daya Beda dan Tingkat Kesukaran Tes Kemamapuan Pemecahan Masalah Matematika Siswa...263
Lampiran 12 Data Skor Kemampuan Penalaran matematika dan Sikap Siswa Terhadap Matematika...270
Lampiran 13 Data Skor Kemampuan Penalaran matematika dan Sikap Siswa Terhadap Matematika...290
Lampiran 14 Lembar Observasi Kegiatan Guru...310
1
BAB I
PENDAHULUAN
1.1.Latar Belakang
Perkembangan Ilmu Pengetahuan, Teknologi dan Sain (IPTEKS) sangat
pesat dan menuntut peningkatan sumber daya manusia bagi suatu bangsa.
Kemajuan teknologi dibidang komunikasi dan informasi datang dari berbagai
penjuru dunia secara cepat dan pesat. Untuk tampil unggul pada keadaan yang
selalu berubah dan kompetitif ini, kita perlu memiliki kemampuan memperoleh,
memilih dan mengelola informasi secara efektif. Dengan adanya penguasaan dan
peningkatan ilmu pengetahuan dan teknologi ini diharapkan bangsa kita mampu
bersaing dan tidak tertinggal dengan bangsa-bangsa lain di dunia sehingga dapat
mengangkat harkat dan martabat bangsa.
Matematika dipandang sebagai ratunya ilmu (Queen of Sciences) dan juga
merupakan ilmu dasar atau pengetahuan dasar yang menopang dan mendukung
perkembangan ilmu pengetahuan dan teknologi. Andi Hakim (1980) dalam
bukunya mengatakan bahwa dibalik setiap teknologi yang membuat kita dapat
menghemat tenaga, sumber daya dan pikiran, telah digunakan terlebih dahulu
berbagai hasil pemikiran matematika. Kemudian Kline mengatakan (dalam Tim
MKPBM Jurusan Pendidikan Matematika, 2001) bahwa matematika itu bukanlah
pengetahuan yang menyendiri yang dapat sempurna karena dirinya sendiri, tetapi
adanya matematika itu terutama untuk membantu manusia dalam memahami dan
menguasai permasalahan sosial, ekonomi, dan alam. Dari beberapa pendapat
2
menduduki peranan penting dan menopang serta mendukung perkembangan ilmu
pengetahuan dan teknonogi.
Matematika merupakan pelajaran yang sangat penting di dalam
pendidikan formal. Dalam Undang-undang Republik Indonesia nomor 20 tahun
2003 tentang Sistem Pendidikan Nasional BAB X pasal 37 tertulis ”Kurikulum
pendidikan untuk jenjang pendidikan dasar dan pendidikan menengah wajib
memuat: (a) pendidikan agama, (b) pendidikan kewarganegaraan, (c) bahasa,
(d) matematika, (e) ilmu pengetahuan alam, (f) ilmu pengetahuan sosial, (g) seni
dan budaya, (h) pendidikan jasmani dan olahraga, (i) keterampilan/kejuruan dan
(j) muatan lokal”. Ini berarti setiap siswa yang berada pada jenjang Pendidikan
Dasar dan Menengah wajib mengikuti pelajaran matematika. Menurut Ismail
(2003) yang menyatakan bahwa: Matematika sebagai salah satu bidang studi,
diberikannya pelajaran matematika di setiap jenjang pendidikan dengan bobot
yang kuat menunjukkan bahwa salah satu bidang studi di sekolah kedudukan
pelajaran matematika di sekolah sangat penting. Hal senada dinyatakan Niss
(Hadi, 2005) bahwa: Salah satu alasan utama diberikan matematika kepada
siswa-siswi di sekolah adalah untuk memberikan kepada individu pengetahuan yang
dapat membantu mereka mengatasi berbagai hal dalam kehidupan, seperti
pendidikan atau pekerjaan, kehiduapan pribadi, kehidupan sosial, dan kehidupan
sebagai warga Negara. Dari uraian di atas dapat disimpulkan bahwa matematika
merupakan pelajaran yang sangat penting dalam pendidikan formal, diantaranya
dapat membantu para siswa mengatasi berbagai hal dalam kehidupan mereka.
Pentingnya peranan matematika dalam menopang serta mendukung
3
kualitas pendidikan matematika yang sesunguhnya. Meskipun matematika
merupakan mata pelajaran disekolah yang sangat penting dan salah satu mata
pelajaran di dalam pendidikan formal yang telah diajarkan sejak jenjang
pendidikan sekolah dasar hingga sekolah lanjutan atas pada kenyataannya,
matematika masih merupakan pelajaran yang sulit, rumit, tidak menarik dan
membosankan untuk dipelajari oleh siswa bahkan merupakan pelajaran yang
menakutkan bagi sebagian besar siswa. Hal ini dikemukakan oleh Ruseffendi
(2001) bahwa matematika (ilmu pasti) bagi anak-anak pada umumnya merupakan
mata pelajaran yang tidak disenangi, kalau bukan sebagai mata pelajaran yang
dibenci. Selain itu Sriyanto (2006) mengatakan bahwa pelajaran matematika di
sekolah sering kali menjadi momok, siswa menganggap matematika pelajaran
yang sulit, anggapan tersebut tidak terlepas dari persepsi yang berkembang dalam
masyarakat tentang matematika merupakan ilmu yang abstrak, penuh dengan
lambang-lambang dan rumus-rumus yang membingungkan, yang muncul atas
pengalaman kurang menyenangkan ketika belajar disekolah. Dari uraian diatas
jelas bahwa pelajaran matematika masih merupakan pelajaran yang sulit, rumit,
membosankan dan tidak disenangi siswa. Hal ini berdampak pada hasil belajar
matematika yang rendah dan sangat berakibat buruk bagi perkembangan
pendidikan matematika kedepan. Selain itu satu hal yang sangat penting dalam
menunjang peningkatan prestasi belajar matematika yaitu kemampuan
matematika yang dimiliki siswa itu sendiri.
Kemampuan matematika sangat penting dikembangkan untuk membangun
perkembangan kognitif siswa sebagai upaya meningkatkan hasil belajar siswa.
4
perlu diperhatikan guru dalam melakukan penilaian hasil belajar, yaitu :
1) pemahaman konsep : siswa mampu mendefinisikan konsep, mengidentifikasi,
dan memberi contoh atau bukan contoh dari konsep tersebut. 2) prosedur : siswa
mampu mengenali prosedur atau proses menghitung yang benar dan tidak benar.
3) Komunikasi : siswa mampu menyatakan dan menafsirkan gagasan matematika
secara lisan, tertulis atau mendemonstrasikan. 4) Penalaran : siswa mapu
memberikan alasan induktif dan deduktif sederhana. 5) Pemecahan masalah :
siswa mampu memahami masalah, memilih strategi penyelesaian dan
menyelesaikan masalah. Hal itu sejalan dengan tujuan umum pembelajaran
matematika yang dirumuskan National Council of Teacher of Mathematics (2000)
yaitu : (1) belajar untuk komunikasi (mathematical communication) ; (2) belajar
untuk bernalar (mathe- matical reasioning); (3) belajar untuk memecahkan
masalah (mathematical problem solving) ; (4) belajar untuk mengaitkan ide
(mathematical connections ); (5) pembentukan sikap positif terhadap matematika
(positive attitutes towart matematics), (Somakim, 2010). Dari uraian di atas
menunjukan bahwa kemampuan matematika siswa merupakan faktor yang sangat
penting bagi perkembangan kognitif siswa dan mempengaruhi hasil belajar siswa.
Salah satu penyebab lemahnya kemampuan siswa dalam memahami
konsep matematika adalah kurangnya kemampuan bernalar, Wahyudin (1999).
Matematika merupakan sarana untuk menanamkan kebiasaan bernalar di dalam
pikiran orang. Anak yang senang melakukan matematika, kemampuan
bernalarnya akan terlatih dengan baik. Menurut Sumarmo (1987) bahwa kegiatan
bernalar dalam pembelajaran matematika membantu siswa meningkatkan
5
aturan, dan prosedur kepada kemampuan pemahaman. Dari uraian diatas dapat
dinyatakan bahwa lemahnya kemampuan siswa dalam memahami matematika
adalah kurangnya kemampuan siswa dalam bernalar.
Pembelajaran matematika yang dilakukan di SMP dan SMA saat ini tidak
banyak memperdalam logika atau penalaran. Siswa lebih sering diberi soal-soal
perhitungan dengan menggunakan algoritma yang ada tanpa adanya kebebasan
dalam menjawab. Pada umumnya soal-soal yang yang diberikan menuntut
jawaban yang harus sesuai dengan cara dan konsep-konsep diberikan guru. Siswa
tidak diberi kesempatan bernalar untuk menemukan atau menurunkan
konsep-konsep berdasarkan penemuan siswa sendiri. Kurangnya penggunaan kemampuan
bernalar dalam menyelesaikan masalah matematika menyebabkan siswa kesulitan
dalam menyelesaikan suatu persoalan. Sebagai contoh dari hasil tes persoalan
kemampuan penalaran matematika siswa materi tentang dimensi tiga yang
dilakukan penulis terhadap 60 orang siswa kelas X SMA Negeri 1 Gebang tahun
pelajaran 2012/2013 yang diambil secara acak adalah sebagai berikut :
Diketahui sebuah kubus ABCDEFGH (seperti gambar 1.1), Jika panjang rusuknya adalah 4 cm maka panjang diagonal sisi AC adalah 4√2 cm. Jika
panjang rusuknya adalah 5 cm maka panjang diagonal sisi AC adalah 5√2
cm. Berapakah panjang diagonal sisinya jika panjang rusuknya 10 cm, apa
yang dapat kamu simpulkan dengan panjang diagonal sisinya jika panjang rusuknya a cm?
Gambar 1.1 Sebuah kubus ABCDEFGH
A B
C D
E
G
6
Meskipun pada jenjang pendidikan sebelumnya yaitu di SMP materi
dimensi tiga ini sudah pernah diajarkan yaitu dalam pelajaran kubus dan balok,
tetapi sebahagian besar siswa masih mengalami kesulitan dan tidak dapat
menjawab soal dengan benar. Dari hasil tes tersebut terlihat bahwa kemampuan
penalaran matematika siswa untuk menggeneralisasi masih rendah. Dari 60 siswa
yang mengikuti tes didapat hanya 7 orang (12%) saja yang menjawab dengan
benar, 18 orang (30%) menjawab dengan kesalahan berhitung dan selebihnya
58% tidak menjawab sama sekali. Pada persoalan ini, sebagian siswa masih
mengalami kesulitan bernalar dengan generalisasi untuk menentukan panjang
rusuk sebuah kubus yang diketahui panjang diagonal sisinya. sehingga
disimpulkan bahwa siswa merasa kesulitan dalam menyelesaikan persoalan yang
didasarkan pada proses berpikir logis (bernalar).
Hasil penelitian menunjukan bahwa penalaran siswa dalam ide geometri
masih rendah, yaitu yang dikemukakan oleh Mistretta (Riyanto, 2011) bahwa
“Carroll found that junior high and senior high school students often lacked
experience in reasoning about geometric ideas”. Demikian pula hasil penelitian
Utari (1987) menyimpulkan bahwa baik secara keseluruhan maupun
dikelompokan menurut tahap kognitif siswa, skor kemampuan siswa SMU dalam
penalaran matematika masih rendah. Hal ini menunjukkan bahwa kemampuan
penalaran matematika siswa masih rendah.
Dalam kurikulum matematika pemecahan masalah merupakan salah satu
kemampuan matematika (doing math) yang sangat penting. karena dalam proses
pembelajaran maupun penyelesaiannya, siswa dimungkinkan memperoleh
7
untuk diterapkan pada penyelesaian persoalan dalam kehidupan sehari-hari.
Pengalaman dilapangan menunjukkan bahwa kegiatan pemecahan masalah dalam
proses pembelajaran matematika belum dijadikan sebagai kegiatan utama,
sehingga sebagian besar siswa tidak dapat memecahkan persoalan-persoalan yang
dihadapinya dan secara umum kemampuan pemecahan masalah matematika siswa
masih rendah. Sebagai contoh dari persoalan pemecahan masalah berikut :
Pak Ahmad akan membuat penangkar burung berbentuk sebuah balok dengan kerangkanya terbuat dari besi baja (gambar 1.2). Jika perbandingan panjang, lebar dan tinggi penangkar adalah 3 : 2 : 2 dan panjang diagonal ruang penangkar burung tersebut 2√17 meter, berapakah panjang besi baja yang diperlukan?
a. Tuliskan apa yang kamu ketahui dan ditanyakan dari informasi di atas? apakah data yang diketahui cukup untuk menghitung hal yang
ditanyakan?
b. Bagaimana cara menghitung panjang besi baja yang diperlukan? c. Hitunglah panjang besi baja yang diperlukan?
d. Menurut Dina panjang besi baja yang diperlukan adalah 50 meter sedangkan menurut Dita adalah 65 meter. Menurut pendapatmu jawaban siapakah yang benar, Jelaskan jawabanmu?
Gambar 1.2 Penangkar burung berbentuk sebuah balok
Pada soal untuk mengukur kemampuan pemecahan masalah siswa
tersebut, dari 60 siswa yang mengikuti tes hanya 5 orang (8%) saja menjawab
dengan benar, 15 orang (25%) menjawab dengan kesalahan berhitung sedangkan
selebihnya tidak menjawab sama sekali. Pada persoalan pemecahan masalah ini
siswa kurang mampu membuat model matematika yang merupakan
8
langkah dalam merencanakan penyelesaian yang selanjutnya menyelesaikan
persoalan tersebut. Berikut ini sampel jawaban salah satu dari 5 orang yang
menjawab soal diatas.
a. Diketahui : perbandingan panjang, lebar dan tinggi adalah 3 : 2 : 2
panjang diagonal ruangnya = 2√17 meter
ditanya : panjang besi baja yang digunakan
data yang diketahui cukup untuk menghitung hal yang ditanyakan.
b. Menggunakan rumus, = 2+ 2
c. Jika p = 3 m, maka l = 2 m dan t = 2 m sehingga didapat,
diagonal sisi alas = 32+ 22 = 9 + 4 = 13
diagonal ruang = 13
2
+ 22 = 13 + 4 = 15
meter
Jika p = 6 m, maka l = 4 m dan t = 4 m sehingga didapat,
diagonal sisi alas = 62+ 42 = 36 + 16 = 52
diagonal ruang 52
2
+ 42 = 52 + 16 = 68 = 2 17
meter
berarti panjangnya = 6 meter, lebarnya = 4 meter dan tingginya = 4 meter
dengan demikian panjang besi baja yang diperlukan adalah :
4 x 6 m + 4 x 4 m + 4 x 4 m = 56 m.
d. Jawaban Dina panjang besi baja yang diperlukan adalah 50 meter salah
sedangkan menurut Dita adalah 65 meter juga salah. Jawaban yang benar
panjang besi baja yang diperlukan adalah 56 meter.
Berdasarkan pola pengerjaan siswa tersebut, dapat dilihat bahwa siswa
masih mencoba-coba untuk menentukan panjang, lebar dan tinggi penangkar
9
faktor pengali pada perbandingan panjang, lebar dan tinggi untuk bilangan yang
besar maka akan membutuhkan cara yang berulang-ulang. Dalam hal ini terlihat
bahwa siswa masih belum mampu membuat suatu perencanaan penyelesaian
masalah dan model matematika dari suatu situasi atau masalah sehari-hari, dimana
perencanaan penyelesaian masalah dan model matematika merupakan indikator
dalam pemecahan masalah. Kemampuan pemecahan masalah matematika masih
dianggap sebagai bagian yang paling sulit dalam matematika, baik dari tingkat
sekolah dasar maupun tingkat sekolah menengah.
Dalam menyelesaikan soal yang yang berhubungan dengan kemampuan
pemecahan masalah matematika sebagaimana diungkapkan Sumarmo (Suhenri,
2006) bahwa kemampuan siswa dalam menyelesaikan masalah matematika pada
umumnya belum memuaskan. Hal senada diungkapkan Nurdalilah (2013) bahwa
pemecahan masalah merupakan suatu tingkat aktivitas intelektual yang tinggi,
serta siswa didorong dan diberi kesempatan seluas-luasnya untuk berinisiatif dan
berfikir sistematis dalam menghadapi suatu masalah dengan menerapkan
pengetahuan yang didapat sebelumnya, namun di lapangan menunjukkan bahwa
kemampuan pemecahan masalah siswa masih rendah. Uraian di atas menunjukan
bahwa kemampuan pemecahan masalah matematika siswa masih rendah.
Berdasarkan beberapa kelemahan siswa dalam menjawab soal yang
diujikan dalam bentuk penalaran dan pemecahan masalah seperti diatas diyakini
sebagai indikasi hasil ulangan harian yang diperoleh sebagian besar siswa selalu
dibawah nilai Kriteria Ketuntasan Minimal (KKM) pada pelajaran matematika
10
kelas X semester ganjil tahun pelajaran 2012/2013 SMA Negeri 1 Gebang, dapat
dilihat pada tabel 1.1
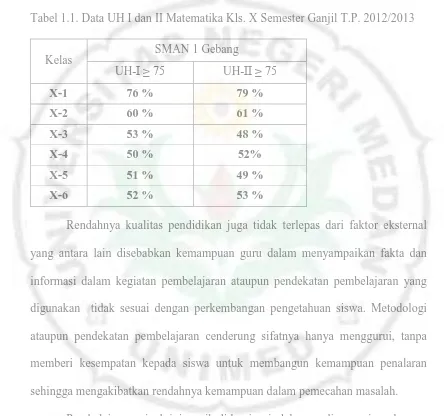
Tabel 1.1. Data UH I dan II Matematika Kls. X Semester Ganjil T.P. 2012/2013
Kelas
SMAN 1 Gebang
UH-I ≥ 75 UH-II ≥ 75
X-1 76 % 79 %
X-2 60 % 61 %
X-3 53 % 48 %
X-4 50 % 52%
X-5 51 % 49 %
X-6 52 % 53 %
Rendahnya kualitas pendidikan juga tidak terlepas dari faktor eksternal
yang antara lain disebabkan kemampuan guru dalam menyampaikan fakta dan
informasi dalam kegiatan pembelajaran ataupun pendekatan pembelajaran yang
digunakan tidak sesuai dengan perkembangan pengetahuan siswa. Metodologi
ataupun pendekatan pembelajaran cenderung sifatnya hanya menggurui, tanpa
memberi kesempatan kepada siswa untuk membangun kemampuan penalaran
sehingga mengakibatkan rendahnya kemampuan dalam pemecahan masalah.
Pembelajaran sejauh ini masih didominasi oleh guru dimana siswa kurang
dilibatkan sehingga mengakibatkan kesan yang monoton dan timbul kejenuhan
pada siswa. Pembelajaran terpusat pada guru diawali dengan pemberian informasi
dalam bentuk ceramah kemudian memulai dengan menerangkan suatu konsep,
pola/ aturan/ dalil, kemudian guru memeriksa (mengecek) apakah siswa sudah
mengerti atau belum, selanjutnya guru memberikan contoh-contoh soal aplikasi
konsep itu, pada akhirnya guru meminta murid untuk menyelesaikan soal-soal.
11
ataupun mengemukahkan pendapatnya sendiri sehingga menumbuhkan kreativitas
dan inovatif siswa dan menyenangkan bagi siswa untuk mengikuti pembelajaran.
Pemilihan model pendekatan pembelajaran hendaknya disesuaikan dengan
kemampuan berpikir dan taraf perkembangan kognitif siswa sehingga dapat
membangkitkan dan mendorong timbulnya aktivitas siswa untuk meningkatkan
kemampuan penalaran dan pemecahan masalah siswa terhadap materi pelajaran
tertentu.
Disamping kemampuan penalaran dan pemecahan masalah yang dimiliki
siswa perlu juga adanya sikap siswa terhadap mata pelajaran matematika yang
dipelajari. Pada saat kegiatan pembelajaran matematika berlangsung persoalan
yang selalu muncul adalah sikap siswa terhadap matematika, dan sikap yang
ditunjukan siswa pada umumnya rendah, kurang menyenangi, bosan, bahkan
cenderung membencinya. Sikap siswa dalam belajar matematika adalah
kecenderungan prilaku seseorang antara sangat suka, suka, tidak suka dan sangat
tidak suka ketika ia belajar matematika, sikap terhadap pendekatan pembelajaran,
serta sikap terhadap soal-soal matematika. Sebagaimana yang diungkapkan Neale
(dalam Saragih 2007) bahwa sikap sebagai ukuran suka atau tidak suka seseorang
terhadap matematika yaitu kecendrungan seseorang untuk terikat atau
menghindari dari kegiatan matematika.
Sedangkan sikap menurut Trow (dalam H. Djaali, 2006) adalah sebagai
kesiapan mental atau emosional dalam beberapa jenis tindakan pada situasi yang
tepat. Mental yang tidak siap cenderung akan menimbulkan kegelisahan, jenuh,
bahkan terjadi pemberontakan untuk menolak setiap apa yang akan disampaikan
12
dalam proses pembelajaran matematika. Seperti yang dikemukakan Gable (dalam
H. Djaali, 2006) bahwa kecendrungan guru hanya mengejar target kurikulum
tanpa memperhatikan sikap mental peserta didik, guru tidak memberikan respon
untuk setiap individu. Berdasarkan uraian diatas sikap siswa terhadap matematika
dapat diartikan sebagai prilaku seseorang antara sangat suka, suka, tidak suka dan
sangat tidak suka terhadap matematika.
Ruseffendi (1991) mengatakan bahwa, anak-anak menyenangi matematika
hanya pada permulaan mereka berkenalan dengan matematika yang sederhana,
makin tinggi tingkatan sekolahnya semakin sukar matematika yang dipelajari
akan semakin kurang minatnya. Menurut Sriyanto (2004) pelajaran matematika di
sekolah sering kali menjadi momok, siswa mengganggap matematika pelajaran
yang sulit, anggapan tersebut tidak terlepas dari persepsi yang berkembang dalam
masyarakat tentang matematika merupakan ilmu yang abstrak, penuh dengan
lambang-lambang dan rumus-rumus yang membingungkan, yang muncul atas
pengalaman kurang menyenangkan ketika belajar matematika di sekolah. Hal
senada dinyatakan Nurdalila (2013) bahwa Sikap siswa terhadap matematika
cenderung negatif dan sebagian siswa tidak menyukai matematika. Hal ini
menunjukan sikap siswa terhadap matematika banyak yang bersifat pasif dan
tidak menyenangkan.
Salah satu pendekatan pembelajaran matematika yang akhir-akhir ini
dibicarakan orang adalah menggunakan pendekatan matematika realistik.
Pendekatan matematika realistik (PMR) adalah suatu teori dalam pendidikan
13
Teori ini berdasarkan pada ide bahwa matematika adalah aktivitas manusia
dan matematika harus di hubungkan secara nyata terhadap konteks kehidupan
sehari-hari siswa sebagai suatu sumber pengembangan dan sebagai area aplikasi
melalui proses matematisasi baik horizontal maupun vertikal. Pendekatan
Matematika Realistik (PMR) dikembangkan berdasarkan pemikiran Hans
Freudenthal yang berpendapat bahwa matematika merupakan aktivitas insani
(human activities) dan harus dikaitkan dengan realitas.
Pendekatan matematilka realistik (PMR) mempunyai ciri antara lain,
bahwa dalam proses pembelajaran siswa harus diberikan kesempatan untuk
menemukan kembali (to reinvent) matematika melalui bimbingan guru
(Gravemeijer, 1994), dan bahwa penemuan kembali (reinvention) ide dan konsep
matematika tersebut harus dimulai dari penjelajahan berbagai situasi dan
persoalan “dunia riil” (de Lange, 1995). Dunia riil diperlukan untuk
mengembangkan situasi kontekstual dalam menyusun materi kurikulum. Materi
kurikulum yang berisi rangkaian soal-soal kontekstual akan membantu proses
pembelajaran yang bermakna bagi siswa. Dalam PMR, proses belajar mempunyai
peranan penting. Rute belajar (learning route) di mana siswa mampu menemukan
sendiri konsep dan ide matematika, harus dipetakan (Gravemeijer, 1997). Sebagai
konsekuensinya, guru harus mampu mengembangkan pengajaran yang interaktif
dan memberikan kesempatan kepada siswa untuk memberikan kontribusi terhadap
proses belajar mereka.
Dari suatu penelitian kuantitatif dan kualitatif yang pernah dilakukan ada
suatu hasil yang menunjukan bahwa siswa didalam pembelajaran matematika
14
memperoleh pembelajaran dengan pendekatan tradisional. Beberapa penelitian
pendahuluan dibeberapa negara menunjukan bahwa pembelajaran menggunakan
pendekatan realistik sekurang-kurangnya dapat membuat matematika lebih
menarik, relefan, bermakna, tidak terlalu formal dan tidak terlalu abstrak,
mempertimbangkan tingkat kemampuan siswa, menekankan belajar matematika
pada learning by doing, mempasilitasi penyelesaian masalah matematika dengan
tanpa menggunakan penyelesaian (algoritma) yang baku, menggunakan konteks
sebagai titik awal pembelajaran matematika (Kuiper dan Knuver, 1993).
Salah satu filosofi yang mendasari pendekatan matematika realistik adalah
bahwa matematika bukanlah suatu kumpulan, aturan atau sifat-sifat sudah lengkap
yang harus siswa pelajari. Menurut Freudental (dalam Fajar Shadiq, 2004) bahwa
matematika bukan merupakan suatu objek yang siap saji untuk siswa, melainkan
bahwa matematika adalah suatu pelajaran yang dinamis dan dapat dipelajari
dengan cara mengerjakannya. Pembelajaran dengan pendekatan matematika
realistik dianggap mampu meningkatkan penalaran dan pemecahan masalah
matematika siswa serta sikap siswa dalam pembelajaran matematika. Pada faktor
internal siswa dituntut untuk dapat memiliki penalaran dan pemecahan masalah
matematika serta sikap positif dalam pembelajaran matematika sedangkan dengan
faktor eksternal yang menyangkut guru dan model atau pendekatan pembelajaran
yang bervariasi akan dapat meningkatkan prestasi siswa dalam pelajaran
matematika.
Berdasarkan uraian diatas, dirasa perlu upaya peningkatan kemampuan
penalaran dan pemecahan masalah matematika siswa di dalam proses
15
kemampuan penalaran dan pemecahan masalah matematika serta sikap siswa
terhadap matematika adalah pendekatan pembelajaran matematika realistik. Hal
itulah yang mendorong penulis sebagai pengajar tertarik untuk melakukan
penelitian yang berjudul Pengaruh Pendekatan Matematika Realistik terhadap
Kemampuan Penalaran dan Pemecahan Masalah Matematika Siswa SMA.
1.2. Identifikasi Masalah
Berdasarkan uraian pada latar belakang di atas kiranya dapat diidentifikasi
beberapa permasalahan dalam pembelajaran matematika di SMA Negeri 1
Gebang, yaitu :
1. Hasil belajar matematika siswa masih rendah.
2. Kemampuan penalaran matematika siswa masih rendah.
3. Kemampuan pemecahan masalah matematika siswa masih rendah
4. Proses pembelajaran berjalan monoton, pendekatan pembelajaran yang
digunakan guru belum bervariasi.
5. Sikap siswa terhadap pelajaran matematika pasif dan tidak menyenangkan
6. Siswa belum mampu menyatakan masalah dalam kehidupan nyata kedalam
matematika.
1.3.Pembatasan Masalah
Dari masalah-masalah yang teridentifikasi sesuai dengan latar belakang
masalah dalam pembelajaran matematika di SMA negeri 1 Gebang penulis
memberikan pembatasan masalah sebagai berikut :
1. Kemampuan penalaran matematika siswa masih rendah, menjadi kendala
16
2. Kemampuan pemecahan masalah matematika siswa masih rendah, menjadi
kendala dalam proses pembelajaran matematika.
3. Sikap siswa terhadap pelajaran matematika rendah.
4. Penggunaan pendekatan matematika realistik belum dipahami dan
dilaksanakan oleh guru matematika.
1.4.Rumusan Masalah
Dari latar belakang masalah dan identitas masalah diatas, yang menjadi
rumusan masalah dalam penelitian ini secara umum adalah :
Bagaimanakah pengaruh pendekatan matematika realistik terhadap
kemampuan penalaran dan pemecahan masalah matematika siswa?
Dari rumusan masalah diatas, peneliti merinci rumusan masalah tersebut menjadi :
1. Apakah kemampuan penalaran matematika siswa yang diberi pembelajaran
dengan pendekatan matematika realistik lebih baik dari pada kemampuan
penalaran matematika siswa yang diberi pembelajaran konvensional?
2. Apakah kemampuan pemecahan masalah matematika siswa yang diberi
pembelajaran dengan pendekatan matematika realistik lebih baik dari pada
kemampuan pemecahan masalah matematika siswa yang diberi pembelajaran
konvensional?
3. Apakah terdapat interaksi antara pembelajaran dan sikap siswa terhadap
kemampuan penalaran matematika siswa?
4. Apakah terdapat interaksi antara pembelajaran dan sikap siswa terhadap
17
1.5.Tujuan Penelitian
Adapun yang menjadi tujuan dalam penelitian ini adalah :
1. Untuk mengetahui apakah kemampuan penalaran matematika siswa yang
diberi pembelajaran dengan pendekatan matematika realistik lebih baik dari
pada kemampuan penalaran matematika siswa yang diberi pembelajaran
konvensional.
2. Untuk mengetahui apakah kemampuan pemecahan masalah matematika siswa
yang diberi pembelajaran dengan pendekatan matematika realistik lebih baik
dari pada kemampuan pemecahan masalah matematika siswa yang diberi
pembelajaran konvensional.
3. Untuk mengetahui apakah terdapat interaksi antara pembelajaran dan sikap
siswa terhadap kemampuan penalaran matematika siswa.
4. Untuk mengetahui apakah terdapat interaksi antara pembelajaran dan sikap
siswa terhadap kemampuan pemecahan masalah matematika siswa.
1.6.Manfaat Penelitian
Hasil penelitian ini diharapkan dapat memberikan manfaat dan masukan
kepada pihak-pihak terkait, diantaranya :
1. Untuk peneliti
1) Memberikan gambaran atau informasi tentang kemampuan penalaran dan
pemecahan masalah matematika siswa yang diberi pembelajaran dengan
pendekatan matematika realistik, kemampuan penalaran dan pemecahan
masalah matematika siswa yang diberi pembelajaran konvensional, interaksi
18
matematika dan interaksi antara pembelajaran dengan sikap siswa terhadap
kemampuan pemecahan masalah matematika siswa
2) Memberikan konstribusi sebagai acuan dalam upaya mengembangkan dan
menerapkan pembelajaran dengan pendekatan matematika realistik untuk
meningkatkan kemampuan matematika siswa, khususnya kemampuan
penalaran dan pemecahan masalah matematika siswa pada setiap
pembelajaran.
2. Untuk Guru.
1) Memberikan masukan kepada guru, khususnya guru mata pelajaran
matematika tentang kemampuan penalaran dan pemecahan masalah
matematika siswa yang memperoleh pembelajaran dengan pendekatan
matematika realistik, kemampuan penalaran matematika siswa dan
pemecahan masalah matematika siswa yang memperoleh pembelajaran
konvensional, interaksi antara pembelajaran dengan sikap siswa terhadap
kemampuan penalaran matematika dan interaksi antara pembelajaran
dengan sikap siswa terhadap kemampuan pemecahan masalah matematika
siswa.
2) Memberikan alternatif kepada guru untuk menggunakan pembelajaran
dengan pendekatan matematika realistik dalam upaya meningkatkan
kemampuan matematika siswa khususnya kemampuan penalaran dan
19
3. Untuk siswa.
1. Penerapan pembelajaran dengan pendekatan matematika realistik dapat
memberi motivasi, meningkatkan kreativitas, dan menumbuhkan inovatif
siswa dalam kegiatan pembelajaran matematika.
2. Penerapan pembelajaran dengan pendekatan matematika realistik dapat
memberikan pengaruh yang lebih baik terhadap kemampuan penalaran dan
1
BAB V
SIMPULAN DAN SARAN
5.1. Simpulan
Berdasarkan hasil pelaksanaan dan analisis statistik data penelitian yang
dilakukan di SMA Negeri 1 Gebang, diperoleh kesimpulan :
Pengaruh pendekatan matematika realistik terhadap kemampuan penalaran dan
pemecahan masalah matematika siswa lebih baik dari pada pembelajaran
konvensional.
Dan rincian dari kesimpulan tersebut adalah sebagai berikut :
1. Kemampuan penalaran matematika siswa yang diberi pembelajaran dengan
pendekatan matematika realistik lebih baik dari pada kemampuan penalaran
matematika siswa yang diberi pembelajaran konvensional.
2. Kemampuan pemecahan masalah matematika siswa yang diberi pembelajaran
dengan pendekatan matematika realistik lebih baik dari pada kemampuan
pemecahan masalah matematika siswa yang diberi pembelajaran
konvensional.
3. Terdapat interaksi antara pendekatan pembelajaran dan sikap siswa terhadap
kemampuan penalaran matematika siswa. Dengan demikian, ada kontribusi
secara bersama-sama yang disumbangkan oleh pembelajaran dengan sikap
siswa terhadap kemampuan penalaran matematika siswa.
4. Terdapat interaksi antara pendekatan pembelajaran dan sikap siswa terhadap
kemampuan pemecahan masalah matematika siswa. Dengan demikian, ada
2
dengan sikap siswa terhadap kemampuan pemecahan masalah matematika
siswa.
5.2 Implikasi
Penemuan dalam penelitian menunjukkan kemampuan penalaran
matematika dan pemecahan masalah matematika siswa yang diberikan
pembelajaran dengan pendekatan matematika realistik lebih baik dibandingkan
dengan siswa yang diajarkan melalui pembelajaran konvensional. Hal ini
berimplikasi pada pemilihan model dan pendekatan pembelajaran oleh guru
matematika. Guru matematika di sekolah menengah atas harus mempunyai cukup
pengetahuan teoritis maupun keterampilan dalam memilih pendekatan
pembelajaran yang mampu mengubah siswa lebih aktif, mengkontruksi
pengetahuan sendiri, memberikan kesempatan kepada siswa untuk lebih leluasa
menjawab permasalahan dengan caranya sendiri, mempunyai pengalaman secara
matematik dan mampu melatih komunikasi matematika. Salah satu pendekatan
pembelajaran yang dapat mengubah siswa ke arah yang lebih positif tersebut
adalah pendekatan matematika realistik. Perubahan itu akan mampu melatih
kemampuan penalaran dan pemecahan masalah matematik siswa sejak dini.
Implikasi lainnya yang perlu mendapat perhatian guru adalah dengan
pendekatan matematika realistik akan membuat siswa lebih kritis, berani
mengeluarkan ide dan menghargai pendapat orang lain. Diskusi kelompok yang
merupakan bagian dari proses pembelajaran dengan pendekatan matematika
realistik akan membuat siswa dapat berkomunikasi matematika secara lisan pada
saat mengawali penyelesaian masalah dan secara tulisan disaat mereka
3
saling berkompetisi untuk memberikan yang terbaik bagi kelompoknya, sehingga
suasana kelas akan terlihat lebih dinamis dan siswa merasa senang dalam belajar.
Karakteristik siswa terutama, sikap siswa terhadap kemampuan
matematika siswa dalam hal ini kemampuan penalaran dan pemecahan masalah
matematika siswa harus menjadi perhatian guru. Hal ini sesuai dengan temuan
dalam penelitian yang menunjukkan bahwa siswa yang mempunyai sikap siswa
yang tinggi terhadap matematik secara keseluruhan lebih baik dibandingkan
dengan siswa yang memiliki sikap siswa yang rendah. Sehingga guru dalam
proses pembelajaran dengan model dan pendekatan pembelajaran apapun harus
mampu memberikan motivasi kepada siswa untuk mengubah siswa yang tadinya
memiliki sikap siswa terhadap matematika yang rendah menjadi lebih tinggi.
Sehingga siswa akan lebih mempunyai rasa tanggung jawab dalam keberhasilan
atau kegagalan dalam belajar. Jika siswa sudah mempunyai rasa tanggung jawab,
maka siswa akan berusaha keras untuk dapat mencapai suatu keberhasilan.
Dampaknya siswa akan aktif, mempunyai inisiatif atau ide-ide dalam
menyelesaikan suatu permasalahan dengan cara apapun.
5.3 Saran
Berdasarkan hasil penelitian, pembelajaran dengan pendekatan
matematika realistik yang diterapkan pada kegiatan pembelajaran memberikan
hal-hal penting untuk perbaikan. Untuk itu peneliti menyarankan beberapa hal
berikut :
1. Pembelajaran dengan pendekatan matematika realistik hendaknya dapat
4
SMA khususnya dalam meningkatkan kemampuan penalaran dan
kemampuan pemecahan masalah matematika siswa
2. Bagi para guru atau pendidik sebaiknya menciptakan suasana belajar
yang memberi kesempatan kepada siswa untuk berinteraksi sesama
siswa dalam kelompoknya, sesama siswa dalam kelompok yang
berbeda maupun siswa dengan guru dalam mengungkapkan
gagasan-gagasan matematika dengan bahasa dan cara mereka sendiri, sehingga
dalam belajar matematika siswa menjadi berani beragumentasi, lebih
percaya diri dan kreatif.
3. Pembelajaran dengan pendekatan matematika realistik dapat dijadikan
sebagai salah satu alternatif dalam meningkatkan kemampuan penalaran dan
pemecahan masalah matematika siswa pada pokok bahasan bangun ruang
sehingga dapat dijadikan masukan bagi sekolah untuk dikembangkan sebagai
strategi pembelajaran yang efektif untuk pokok bahasan matematika yang
lain.
4. Mengingat karakteristik PMR yang memungkinkan siswa untuk
mengembangkan kemampuan penalaran dan pemecahan masalah matematika
siswa SMA maka peneliti selanjutnya dapat mengkaji kemampuan
matematika yang lain untuk dapat dikembangkan melalui pembelajaran
171
DAFTAR PUSTAKA
Andi Hakim Nasoetion. 1980. Landasan Matematika. Jakarta; Penerbit Bhratara Karya Aksara.
Arikunto, S., 2006, Dasar-Dasar Evaluasi Pendidikan, Penerbit Bumi Aksara, Jakarta.
Cronbach, J.L. 1954. Educational Psychology. New York : Harcourt Book and Company
Dahlan, J.A. (2004). Meningkatkan Kemampuan Penalaran dan Pemahaman Matematik Siswa Sekolah Menengah Lanjutan Pertama melalui Pendekatan Pembelajaran Open-Ended. Disertasi PPS UPI Bandung: Tidak diterbitkan.
--- (1995). “No Change Without Problems”. In T.A. Romberg(Ed). Reform in School Mathematics and Authentic Assessmen. Albany : State University of New York Press.
De Lange, J. (1996). “Using and Applying Mathematics in Education”. in: A.J. Bishop, et al. (eds). 1996. International handbook of mathematics education, Part one. 49-97. Kluwer academic publisher.
Depdiknas. (2003). Model Pembelajaran Matematika Sekolah Dasar. Jakarta: Dikdasmen.
--- (2006). Kurikulum Tingkat Satuan Pendidikan SMA/MA. Tersedia online pada http://www.puskur.co.id, Juli 2007.
Djaali, H. (2006). Pengukuran dalam Bidang Pendidikan. Jakarta, P.T.Gramedia Widiasarana Indonesia
Dimyati dan Mudjiono, 1999 : Belajar dan Pembelajaran. Jakarta : Rinoke Fajar Shadiq dan Nur Amini Mustajab, (2010) : Pembelajaran Matematika
Dengan Penedekatan Realistik di SMP. Jakarta, Pusat Pengembangan dan Pemberdayaan Pendidikan dan Tenaga Kependidikan (PPPPTK) Matematika.
Gagne.RM, 1985. The Condition of Learning and Theory of Instruction, Fourth Edition. New York : Holt, Rine Hart and Winston. (1999). Manulis Jurnal Sebagai Strategi Dalam Proses Pembelajaran Matematika di SMP, Makalah, Surabaya.
Gagne, and Briggs. (1997). The Conditioning of Learning. New York: Holt Rinchard and Winston.
Gravemeijer, K.P.E. (1994). Developing Realistic Mathematics Education. Culemborg: Technipress.
---1997. Developing Realistic Mathematics Education. Utrecht : CD-b Press. The Netherlands
Gutek, G.L. 2004. History Of Educational. Microsoft Encarta Reference Library.
Hadi, S. 2005. Pendidikan Matematika Realistik dan Implementasinya. Banjarmasin : Tulip
172
Hudoyo, H. (1979). Pengembangan Kurikulum Matematika dan Pelaksanaannya di Depan Kelas. Surabaya: Usaha Nasional.
---(1988). Mengajar Belajar Matematika. Jakarta; Depdikbud Dikti PLPTK.
Human Development Index-2011 ranking. Melalui <http://hdr.unpd.org/en/
statistic.com˃ didownload 30 Desember 2011
Hurley. (1982) Logic. California: Wadsworth Publishing Company.
Ismail, dkk. 2003. Kapita Selekta Pembelajaran Matematika. Jakarta : Universitas Terbuka
Jihad, A. 2006. Meningkatkan Kemampuan Pemecahan Masalah Matematik Siswa dengan Metode IMPROVE disertai Embedded test (Studi Eksperimen di Madrasah Aliyah Negeri 2 Bandung. Tesis Tidak Dipublikasikan Bandung: Pascasarjana. UPI Bandung.
Kingsley, H.L. dan Garry R., 1957. The Nature and Condition of Learning. Englewood Cliffs, New Jersey : Prentice-Hall Inc.
Kuiper, W. and Knuver, A. (1993). The Netherlands TIMMS Studies.
Matlin, M.W. (1994). Cognition. Third Edition. Amerika: Harcourt Brace Publishers.
Mouly, George W, (1968). Psychology for Effective Teaching. New York : Holt, Rinehart and Winston Inc.
Narbuko. Ch dan Abu Achmadi. (2010). Metodologi Penelitian. Jakarta; Bumi Aksara
Nasution, S. 1982. Berbagai Pendekatan Dalam Proses Belajar Mengajar. Edi Pertama. Jakarta : Bina Aksara.
NCTM. (1989). Curriculum and Evaluation Standards for School Mathematics. [Online]. Tersedia: http://www.nctm.org/focalpoints. [2 Desember 2006]
--- (2000), Defining Problem Solving, [Online].Tersedia:http://www. learner.org/channel/courses/teachingmath/gradesk_2/session_03/sectio_ 03_a.html. [10 September 2009].
Panjaitan, A. (2008). Evaluasi Pembelajaran. Medan: Pascasarjana UNIMED.
Priatna, N. (2002). Kemampuan Penalaran dan Pemahaman Matematika Siswa Kelas III SLTP Negeri di Kota Bandung. Disertasi doktor PPS UPI
Bandung: tidak dipublikasikan.
Rahayu, H.E. 2005. Pengaruh Pembelajaran Matematika dengan Model Pemerolehan Konsep Melalui Pendekatan Realistik pada Pokok Bahasan Volume Bangun Ruang Ditinjau Dari Kemampuan Kognitif. Surakarta: Skripsi UMS tidak diterbitkan.
Ruseffendi, E.T. 1988. Pengantar Kepada Membantu Guru Mengembangkan Kompetensinya dalam Pengajaran Matematika untuk Meningkatkan CBSA. Bandung : Tarsito.
---1991. Pengantar kepada Membantu Guru Mengembangkan Kompetensinya dalam Mengajar Matematika untuk Meningkatkan CBSA. Bandung : Tarsito
173
--- (1994), Dasar-dasar Penelitian Pendidikan dan Bidang Non-Eksakta Lainnya. Semarang: IKIP Semarang Press.
--- (1998). Dasar-dasar Penelitian Pendidikan dan Bidang Non-eksakta Lainnya. IKIP Semarang Press: Semarang.
--- (2001). Dasar-dasar Penelitian Pendidikan dan Bidang Non Eksakta Lainnya. Semarang : IKIP Semarang Press.
Sagala, S. (2003). Konsep dan Makna Pembelajaran untuk Membantu Memecahkan Problematika Belajar dan Mengajar. Bandung: Alfabeta. Saragih, 2007. Mengembangkan Kemampuan Berpikir Logis dan Komunikasi
Matematika Siswa Sekolah Menengah Pertama melalui Pendekatan Matematika Realistik. Disertasi S3 UPI Bandung : tidak dipublikasikan Shadiq F, M.App.Sc, 2004, Penalaran, Pemecahan Masalah, dan Komunikasi dalam Pembelajaran Matematika. Yogyakarta: Depdiknas.
--- (2007). Implikasi Kontruktivisme dalam pembelajaran Matematika Sekolah Dasar. (Online) (http://www. Konstruktivis.wordpress.com diakses 11 Mei 2007)
Silver, E.A. (1997). Fostering Creativity through Instruction Rich in Mathematical Problem Solving and Problem Posing. [Online]. Tersedia: http://66.102.7.104/search?q=cache:Fw8Lg-xQoFwJ:www .fiz-karlsruhe.de/fiz/publications/zdm/zdm973a3.pdf+fostering+
creativity,+Edward+A.+Silver&hl=id
Sanjaya, W., (2006), Strategi Pembelajaran Berorientasi Standar Proses Pendidikan, Kencana Prenada Media Group: Jakarta
Soedjadi, R., (1992), Kiat Pendidikan Matematika di Indonesia (Konstatasi Keadaan Masa Kini Menuju Harapan Masa Depan), Jakarta : Dirjen Dikti Depdiknas.
Soekadijo, R.G. (1999). Logika Dasar. Jakarta: Gremedia.
Sriyanto. 2006, Menebar virus Pembelajaran Matematika yang Bermutu, http://www.pmri.or.id/en/article.php?main=3. Online. Diakses 12 Mei 2011
Sudharta. (2004). Pembelajaran Kontekstual dalam Upaya Mengembangkan Kemampuan Pemecahan Masalah dan Komunikasi Matematik Mahasiswa Calon Guru. Tesis pada PPS UPI Bandung: Tidak diterbitkan.
Suparno, Paul. 1997. Filsafat Kontruktivisme dalam Pendidikan. Yogyakarta: Kanisius.
Suherman, E. dan Winataputra, U. (1993), Strategi Belajar Mengajar Matematika, Jakarta: Universitas Terbuka.
Suherman, E. dkk. 2003. Strategi Pembelajaran Matematika Kontemporer. FMIPA-JICA UPI Bandung: Tidak diterbitkan.
Surakhmad, W. (1982). Pengantar Interaksi Belajar Mengajar: Dasar dan Teknik Metodologi Pengajaran. Bandung : Tarsito
Somakim. (2010). Peningkatan Kemampuan Berpikir Kritis dan Self-Efficacy Matematika Siswa Sekolah Menengah Pertaa dengan Penggunaan Pendekatan Matematika Realistik. Disertasi SPs UPI Bandung: tidak diterbitkan.
174
Sujono (1988). Pengajaran Matematika untuk Sekolah Menengah. Jakarta: Depdikbud, Dikti P2LPTK.
Sumardyono. 2010. Pengertian Dasar Problem Solving. http:// problemsolving. p4tkmatematika. org/2010/02/ pengertian-dasar-problem-solving /. Diakses 1 Juni 2010.
Sumarmo, U. 1987. Kemampuan Pemahaman dan Penalaran Matematika Siswa SMA dikaitkan dengan Kemampuan Penalaran Logik Siswa dan beberapa Unsur Proses Belajar dan Mengajar. Disertasi. FPS IKIP Bandung : tidak dipublikasikan.
--- (2005). “Pembelajaran Matematika untuk Mendukung Pelaksanaan
Kurikulum Tahun 2002 Sekolah Menengah”. Makalah pada Seminar Pendidikan Matematika 7 Agustus 2005 Universitas Negeri Gorontalo: Gorontalo.
Suria Sumantri, J.S. 1990 : Filsafat Ilmu Sebuah Pengantar Populer. Jakarta : Sinar Harapan.
Suryadi, D. (2005). Penggunaan Pendekatan Pembelajaran Tidak Langsung serta Pendekatan Gabungan Langsung dan Tidak Langsung dalam Rangka Meningkatkan Kemampuan Berpikir Matematik Tingkat Tinggi Siswa SLTP. Disertasi. PPS UPI Bandung: Tidak diterbitkan.
---(2007). “Pendidikan Matematika”, dalam Ilmu dan Aplikasi Pendidikan. Bandung : Pedagogiana Press.
Tim MKPBM Jurusan Pendidikan Matematika. (2001) Strategi Pembelajaran Matematika Kontemporer. Bandung : JICA-Universitas Pendidikan Bandung (UPI)
Turmudi. (2004). Pengembangan Materi Ajar Matematika Realistik di Sekolah
Dasar. Makalah disampaikan pada Lokakarya Pembelajaran Matematika Realistik Bagi Guru SD di Kota Bandung tgl. 7,13, dan 14 Agustus 2004 UPI Bandung. tidak diterbitkan.
Usman, H. dan Akbar, R. P. S. 2008. Pengantar Statistika. Jakarta: Bumi Aksara. Wahyudin. (1999). Kemampuan Guru Matematika, Calon Guru Matematika, dan
Siswa dalam Mata Pelajaran Matematika. Disertasi IKIP Bandung:
Tidak Dipublikasikan.
--- (2003). “Peranan Problem Solving”. Proceeding National Seminar on Science and Mathematics Education, the Role of IT/ICT in Supporting the Implementation of Competensy-Based Curriculum. Bandung: JICA-IMSTEP.