GEOMETRI ANALITIK DATAR

GEOM ETRI ANALITIK DATAR

Oleh:

Dr. Susanto, M Pd

PROGRAM STUDI PENDIDIKAN M ATEM ATIKA

JURUSAN PENDIDIKAN M ATEM ATIKA DAN IPA

FAKULTAS KEGURUAN DAN ILM U PENDIDIKAN

KATA PENGANTAR

Puji syukur dipanjat kan kehadirat Alloh SWT at as segala rahmat , t aufiq,

dan hidayahNya yang t elah dilim pahkan, sehingga t erselesaikannya buku

pegangan kuliah unt uk mat a kuliah Geomet ri Analit ik Dat ar. M at a Kuliah ini

memuat mat eri t ent ang garis lurus, lingkaran, ellips, hiperbola, parabola, sert a

koordinat dan persamaan kut ub.

Selanjut nya penulis menyadari bahw a buku ini masih belum sempurna;

unt uk it u dimohon t anggapan baik berupa krit ik dan saran kepada pembaca dem i

kebaikan buku pegangan kuliah ini. Akhirnya mudah-mudahan buku ini

bermanfaat bagi pembaca.

DAFTAR ISI

Hal.

HALAM AN JUDUL ……….. i

KATA PENGANTAR ………. ii

DAFTAR ISI ……….. iii

BAB I GARIS LURUS ……….. 1

BAB II LINGKARAN ……….. 12

BAB III ELLIPS ……….. 19

BAB IV HIPERBOLA ……….. 26

BAB V PARABOLA ………... 37

BAB VI KOORDINAT DAN PERSAM AAN KUTUB ……….. 44

BAB I GARIS LURUS

Perhat ikan gambar dibaw ah ini.

M isalkan diket ahui garis AB dengan A(x1 , y1) dan B(x2 , y2). P(x , y) adalah

sebarang t it ik pada garis AB t ersebut . Vekt or-vekt or

OA

,

OB

,

dan

AB

,

masing-masing dit ulis dengan a, b, dan c.

Garis AB dapat didefinisikan dari t it ik A dan B dengan menggunakan vekt or

sebagai berikut .









;



,

y

a

c

x

R

1 2 1 2 1

1

,

(

),

(

,

y

x

y

x

x

y

y

x











)

(

),

(

,

_{1 2 1 2 1}

1

y

y

x

x

y

y

x

x



























1 2

1

1 2

1

y

y

y

y

x

x

x

x

Selanjut nya persamaan diat as dinamakan persamaan garis lurus yang melalui t it ik

A(x1 , y1) dan B(x2 , y2). Y

O

A

B

Perhat ikan gambar diat as,



ON



= n disebut panjang normal garis g. ON t egak lurus pada garis g.



adalah sudut yang diapit oleh normal ON dan sumbu X posit if. Ambil sebarang t it ik P(x,y) pada garis g. Q adalah proyeksi t it ik P pada

sumbu X dan R adalah proyeksi t it ik Q pada ON.



OQR +



= 90o dan



OQR +



PQR = 90o

maka



PQR =



.



OR



=



OQ



Cos



= x Cos





RN



=



PQ



Sin



= y Sin x



RN



=



PQ



Sin



= y Sin x

Perhat ikan bahw a



OR



+



RN



=



ON



, maka x Cos



+ y Sin



= n.

Karena t it ik P sebarang t it ik pada garis lurus g, maka hubungan t erakhir ini

menyat akan persamaan garis g. Persamaan bent uk it u dinamakan persamaan

normal dari Hess at au disingkat persamaan norm al at au persamaan Hess. Karena

n adalah panjang normal, maka n suat u bilangan posit if.

Cont oh

Tent ukan persamaan normal suat u garis lurus dengan panjang normal 5 sat uan

dan besar sudut apit garis t ersebut dengan sumbu arah posit if adalah 135o.

Jaw ab

O

N g

P(x,y)

R

 

Q Y

Persamaan normal garis g adalah:

x cos 45o + y sin 45o = 5

5

2

2

1

2

2

1





y

x

Apabila kedua ruas dari persamaan t ersebut masing-masing dikalikan

2

, maka

diperoleh persamaan:

X + y = 5

2

.

Selanjut nya pandang bent uk umum persamaan garis lurus Ax + By + C = 0. Apabila

kedua ruas persamaan ini dikalikan k dengan k



0, maka diperoleh: KAx + kBy + kC = 0.

Jika dibandingkan dengan persamaan normal, maka diperoleh hubungan

k2A2 + k2B2 = 1

k2(A2 + B2) = 1

k =

2 2

1

B

A





Sehingga persamaan normal dari Ax + By + C = 0 adalah

0

2 2 2

2 2

2



























B

A

C

y

B

A

B

x

B

A

A

Dari normal ini dapat disimpulkan bahw a jarak t it ik asal O ke garis lurus dengan

persamaan Ax + By + C = 0 adalah

2 2

B

A

C





(dipilih harga posit ifnya).

Cont oh

Ubahlah persamaan-persamaan garis lurus berikut ini menjadi bent uk persamaan

normal. Kemudian t ent ukan jarak garis-garis t ersebut masing-masing ke t it ik asal

O.

a) 5x – 12 y = 19

Jaw ab

a) 5x – 12 y – 19 = 0

k =

13

1

169

1

)

12

(

5

1

2

2















Alt ernat if (-19) bilangan negat if, maka harga k dipilih yang bert anda posit if,

sehingga k =

13

1



. Jadi persamaan normal adalah

0

13

19

13

12

13

5







y

x

, sedangkan jarak ke t it ik asal O adalah

13

19

sat uan panjang.

b) 3x – 4y + 10 = 0

k =

2 2

)

4

(

3

1







=

5

1

25

1







Karena 10 adalah bilangan posit if, maka nilai k dipilih yang bert anda negat if, yait u

k =

5

1



Jadi bent uk persamaan normalnya adalah

0

2

5

4

5

3









x

y

, sedangkan jarak ke t it ik asal O adalah 2 sat uan panjang.

Perhat ikan dua garis lurus yang berpot ongan

g1 : y = m1x + n1

Tanjakan garis g1 adalah m1 = tg



, dan t anjankan garis g2 adalah m2 = t g



.



adalah sudut yang dibent uk oleh garis g1 dan garis g2. Selanjut nya akan dicari



, yait u



=



-



.

Sehingga

2 1

2 1 2 1

2

1

1

.

1

)

(

m

m

m

m

arctg

y

Jadi

m

m

m

m

tg

tg

tg

tg

tg

tg

tg

tg









































Dengan memperhat ikan harga-harga t ert ent u dari



dpat dit ent ukan posisi kedua garis t ersebut .

a) Jika



= 0, maka m1 = m2. Ini berart i dua garis t ersebut sejajar at au berimpit . Dua garis t ersebut akan sejajar apabila n1



n2 dan dua garis t ersebut berimpit , apabila n1 = n2.

O Y

X g1

g2

 

b) Jika harga t g



besar t ak berhingga, yait u



= 90o, maka 1 + m1m2 = 0 at au m1 =

-2

1

m

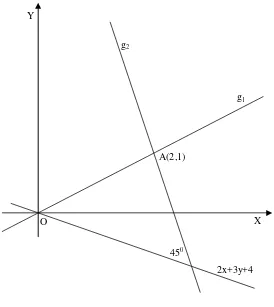
. Ini berart i dua garis t ersebut saling t egak lurus.

Cont oh

Tent ukan persamaan garis lurus yang melalui t it ik A(2,1) dan mengapit sudut yang

besarnya 45o dengan garis 2x + 3y + 4 = 0

[image:9.595.173.447.370.677.2]

Jaw ab

Gambar dibaw ah ini adalah sket sa dari ket ent uan-ket ent uan dalam soal dan garis

g1 dan g2 adalah garis-garis yang mengapit sudut yang besarnya 45o dengan garis

2x+3y+4=0.

Tanjakan garis 2x + 3y + 4 = 0 adalah m =

-3

2

. M isalkan t anjakan garis g1 yang

dicari adalah m1, maka Y

X g2

g1

A(2,1)

2x+3y+4 450

5

1

3

2

3

2

1

3

2

1

3

2

1

45

1

1 1

1 1

1 1





















m

m

m

m

m

m

m

m

m

tg

o

Jadi persamaan garis g1 adalah garis dengan t anjakan m1 =

5

1

dan melalui t it ik A(2

, 1), yait u

Y – 1 =

5

1

(x – 2)

X – 5y + 3 = 0

Tanjakan garis g2 adalah m2 = -5, sehingga persamaan garis g2 adalah

Y – 1 = -5(x – 2)

5x + y – 11 = 0.

Pada persamaan normal suat u garis lurus, dapat langsung dit ent ukan jarak t it ik

asal O ke garis t ersebut . Selanjut nya akan dit ent ukan jarak t it ik sebarang ke garis

lurus t ert ent u.

Y

g g1

T(x1,y1) d

n 

X

Y

d n

N T(x1, y1) g

Pada gambar diat as garis g memiliki persamaan normal x cos



+ y sin



- n = 0 dan t it ik T(x1 , y1) yang berjarak d dari garis g. Dapat dit ent ukan persamaan

normal garis g1 yang melalui t it ik T(x1 , y1) dan sejajar dengan garis g. Jelas bahw a

panjang normal dari garis g1 adalah (n + d), m aka persamaan normal garis g1

adalah x cos



+ y sin



- (n+d) = 0.

Karena t it ik T(x1 , y1) pada garis g1, maka koordinat -koordinat t it ik T memenuhi

persamaan garis g1, sehingga diperoleh

x1 cos



+ y1 sin



- (n + d) = 0 Jadi d = x1 cos



+ y1 sin



- n.

Dengan cara yang sama dapat dit ent ukan pula jarak t ersebut apabila t it ik-t it ik O

dan T t erlet ak sepihak t erhadap garis g, sehingga diperoleh d = -(x1 cos



+ y1 sin



- n)

Karena d adalah jarak, maka nilainya harus posit if, sehingga harus diambil harga

mut laknya.

d =

x

1

cos





y

1

sin





n

Jika persamaan garisnya merupakan persamaan unt uk umum, maka unt uk

menent ukan jarak suat u t it ik pada garis t ersebut harus diubah ke persamaan

normal. Karena persamaan normal garis Ax + By + C = 0 adalah

+

0

2 2 2

2 2

2

























A

B

C

y

B

A

B

x

B

A

A

maka jarak t it ik T(x1 , y1) ke garis t ersebut adalah

d = 2 2 1 1

B

A

C

By

Ax







Bent uk persamaan normal garis y = mx + n adalah

0

1

2























m

n

mx

y

, maka jarak

t it ik T(x1 , y1) ke garis t ersebut adalah d =

Cont oh

Tent ukan jarak t it ik P ke garis g, apabila

a) P(2 , 3) dan g : 3x – 4y – 3 = 0

b) P(-4 , 1) dan g : y = 2x – 1

Jaw ab

a) d =

2 2

)

4

(

3

3

3

.

4

2

.

3









=

5

4

1

5

9



b) d =

5

5

6

5

6

)

2

(

1

1

)

4

(

2

1

2

2















Soal-soal Latihan

1. Gambarlah sepasang sumbu koordinat dan gambarlah kedudukan t it ik-t it ik

dengan koordinat (4 , 1), (-2 , 3), (-1 , -4), (5 , -5), (0 , 6), dan (-5 , 0). Tulislah

koordinat -koordinat nya disamping t it ik t ersebut .

2. Gambarlah sebuah segit iga dengan t it ik-t it ik sudut A(0 , 1), B(2 , 5), dan C(-1 ,

4). Bukt ikan bahw a segit iga t ersebut merupakan segit iga sama kaki.

3. Diket ahui sebuah segit iga dengan t it ik-t it ik sudut P(-3 , 2), Q(0 , -1), dan R(5 ,

4). Bukt ikan bahw a segit iga t ersebut merupakan segit iga siku-siku dan gambar

segit iga t ersebut .

4. Diket ahui ruas garis dengan t it ik-t it ik ujung A(-5 , -6) dan C(10 , 1). Bukt ikan

bahw a t it ik B(4 , -2) t erlet ak pada ruas garis t ersebut .

5. Diket ahui sebuah segit iga dengan t it ik-t it ik sudut nya adalah A(3 , 0), B(-2 , 4),

dan C(-5 , -3). Tent ukan koordinat -koordinat t it ik berat nya. (t it ik berat segit iga

adalah t it ik perpot ongan ket iga garis berat nya).

6. Tit ik P(3 , 0) adalah t it ik pusat sebuah lingkaran t it ik A(-2 , 7) adalah t it ik ujung

sebuah garis t engahnya. Tent ukan koordinat -koordinat t it ik ujung lainnya dari

7. Diket ahui t it ik A(4 , 7). Tent ukan persamaan garis lurus yang sejajar sumbu-x

dan melalui t it ik A. Tent ukan pula persamaan garis lurus yang sejajar sumbu-y

dan melalui t it ik A.

8. Tent ukan persamaan garis lurus yang melalui O(0 , 0) dan P(-2 , 5). Tent ukan

pula t anjakan dari garis lurus t ersebut .

9. Tent ukan t anjakan dan persamaan garis lurus yang melalui O(0 , 0) dan yang

mengapit sudut 60o dengan sumbu-x arah posit if.

10.Diket ahui t it ik A(1 , 4) dan B(3 , -2). Tent ukan t anjakan dan persamaan garis

lurus yang melalui t it ik-t it ik A dan B.

11.Tent ukan persamaan garis lurus dengan t anjakan m =

2

1

dan melalui t it ik (0 ,

4).

12.Carilah persamaan garis lurus yang melalui t it ik (-1 , 2) dan mengapit sudut

135o dengan sumbu-x arah posit if.

13.Tent ukan koordinat -koordinat t it ik-t it ik pot ong dengan sumbu-sumbu

koordinat dan t anjakan garis 3x – 5y + 15 = 0.

14.Suat u lingkaran dengan t it ik pusat (3 , -2) dan t it ik (9 , 2) adalah salah sat u t it ik

ujung sebuah garis t engahnya. Tent ukan koordinat -koordinat t it ik ujung

lainnya dari garis t engah t ersebut .

15.Tent ukan pasangan garis mendat ar (sejajar sumbu-x) yang memot ong sumbu

y di t it ik sejauh 5 sat uan di at as t it ik asal.

16.Tent ukan pasangan garis vert ikal yang memot ong sumbu-x di sebuah t it ik

sejauh 4 sat uan sebelah kiri t it ik asal.

17.Tent ukan persamaan garis lurus yang melalui t it ik (-5 , 1) dengan t anjakan –1.

18.Tent ukan persamaan garis lurus yang t anjakannya adalah

2

1

dan yang

memot ong sumbu-y di sebuah t it ik 7 sat uan dibaw ah t it ik asal.

19.Tent ukan persamaan garis lurus yang t anjakannya adalah –2 dan yang

memot ong sumbu-x di sebuah t it ik 3 sat uan sebelah kanan t it ik asal.

21.Tent ukan persamaan garis lurus yang melalui t it ik (a , 0) dan (0 , b).

22.Tent ukan persamaan garis lurus yang mengapit sudut 45o dengan sumbu-x

arah posit if dan melalui t it ik A(3 , 1).

23.Tent ukan persamaan garis lurus yang melalui t it ik P(2 , 3) dan yang sejajar

dengan garis x + 2y – 3 = 0.

24.Tent ukan persamaan garis lurus yang melalui t it ik T(-1 , -4) dan yang t egak

lurus pada garis x – 2y + 2 = 0.

25.Diket ahui t it ik-t it ik A(1 , 3) dan B(4 , -1). C adalah t it ik t engah ruas garis AB.

Tent ukan persamaan garis lurus yang melalui C dan yang t egak lurus AB.

26.Diket ahui A(-2 , -1) dan B(5 , 5). Tent ukan sumbu ruas garis AB.

27.Ubahlah persamaan garis g berikut menjadi persamaan normal. Kemudian

t ent ukan jarak t it ik P ke garis g.

a) g : 3x – 4y + 5 = 0 dan P(-1 , 3) b) g : 12x + 5y – 19 = 0 dan P(2 , -1).

28.Carilah persamaan garis lurus yang melalui t it ik pot ong garis-garis 11x + 3y – 7

= 0 dan 12x + y – 19 = 0 sert a berjarak sama dari t it ik-t it ik A(3 , -2) dan B(-1 ,

6).

29.Apabila



adalah sudut lancip yang dibent uk oleh garis-garis 2x – y – 3 = 0 dan garis x – 3y + 5 = 0. Tent ukan t g



.

30.Tent ukan panjang normal dari garis 5x – 12y – 13 = 0.

31.Tent ukan persamaan garis berat



ABC yang melalui A dengan A(3 , -1), B(-2 , 4), dan C(6 , -2).

32.Tent ukan persamaan garis yang melalui t it ik asal dan t egak lurus pada garis

yang melalui t it ik-t it ik A(-5 , 1) dan B(2 , 4).

33.Tent ukan persamaan garis yang melalui t it ik (3 , -2) dan mengapit sudut 450

BAB II LINGKARAN

Definisi

Lingkaran adalah himpunan t it ik-t it ik (pada bidang dat ar) yang jaraknya dari suat u

t it ik t ert ent u sama panjangnya.



Pada gambar diat as t it ik pusat lingkaran di O(0 , 0) dan jari-jari r sat uan panjang.

Unt uk menent ukan persamaan lingkaran dapat diambil sebarang t it ik pada

lingkaran m isalnya T(x , y). Jarak t it ik T dan t it ik O adalah

x

2



y

2 . Padahal jarak

t it ik-t it ik t dan t it ik O adalah r, maka diperoleh hubungan bahw a

x

2



y

2 = r at au x2 + y2 = r2.

Karena T(x , y) adalah sebarang t it ik pada lingkaran, maka set iap t it ik pada

lingkaran berlaku x2 + y2 = r2. Jadi persamaan lingkaran dengan pusat O(0 , 0) dan

jari-jari r adalah x2 + y2 = r2.

Dengan cara yang mirip, dapat dit ent ukan persamaan lingkaran dengan pusat t it ik

P(a , b) dan jari-jari r sat uan sebagai berikut .

Y

X T(x,y)

O r

Y

T(x,y)

M isalkan gambar diat as adalah lingkaran dengan pusat P(a , b) dan jari-jari r

sat uan. Unt uk menent ukan persamaan lingkaran ini dapat diambil sebarang t it ik

pada lingkaran, misalnya T(x , y). Jarak t it ik-t it ik T dan P adalah

2 2

)

(

)

(

x



a



y



b

.

Padahal jarak t it ik-t it ik T dan P adalah jari-jari lingkaran yait u r; maka diperoleh

hubungan

(

x



a

)

2



(

y



b

)

2 = r at au (x – a)2 + (y – b)2 = r2.

Karena T(x , y) adalah sebarang t it ik pada lingkaran it u, maka set iap t it ik pada

lingkaran it u memenuhi hubungan t ersebut . Ini berart i bahw a persamaan

lingkaran yang berpusat di t it ik P(a , b) dengan jari-jari r sat uan adalah (x – a)2 + (y

– b)2 = r2.

Cont oh 1

Tent ukan persamaan lingkaran yang berpusat di t it ik (4 , -3) dan berjari-jari 5

sat uan.

(jaw ab: (x – 4)2 + (y + 3)2 = 25).

Cont oh 2

Tent ukan persamaan lingkaran yang berpusat di t it ik P(1 , 3) dan melalui t it ik Q(-2

, 5).

(jaw ab: (x – 1)2 + (y – 3)2 = 13).

Perhat ikan persamaan suat u lingkaran dengan pusat (a , b) dan jari-jari r, yait u

(x – a)2 + (y – b)2 = r2.

Ruas kiri dari persamaan ini dapat diuraikan menjadi:

x2 + y2 + Ax + By + C = 0.

Persamaan bent uk t erakhir ini dinamakan persamaan bent uk umum suat u

lingkaran.

Apabila diket ahui persamaan bent uk umum suat u lingkaran: x2 + y2 + Ax + By + C =

0, maka dapat dicari koordinat -koordinat t it ik pusat dan jari-jarinya. Persamaan

bent uk umum t ersebut dapat diubah menjadi:

x2 + Ax +

4

1

A2 + y2 + By +

4

1

B2 = A2 +

4

1

B2 – C

(x +

2

1

A)2 + (y +

2

1

B)2 = A2 + B2 – C.

Dari persamaan t erakhir ini, dapat disimpulkan bahw a t it ik pusat lingkaran adalah

(-2

1

A ,

-2

1

B) dan jari-jarinya adalah

A

2



B

2



C

4

1

4

1

Cont oh 3

Tent ukan koordinat -koordinat t it ik pusat dan jari-jari sebuah lingkaran dengan

persamaan 4x2 + 4y2 – 4x + 16y – 19 = 0.

(jaw ab: Tit ik pusat nya (

2

1

, -2) dan jari-jari 3.

Cont oh 4

Tent ukan persamaan lingkaran yang melalui t iga t it ik P(1 , 0), Q(0 , 1) dan T(2 , 2).

(jaw ab: 3x2 + 3y2 – 7x – 7y + 4 = 0)

Y

X y = mx + n

Pada gambar diat as diket ahui garis y = mx + n dan lingkaran x2 + y2 = r2.

Selanjut nya dapat dicari persamaan garis singgung pada lingkaran yang sejajar

garis dengan persamaan y = mx + n. Karena garis singgung yang dicari harus

sejajar garis dengan persamaan y = mx + n, maka dapat dimisalkan garis singgung

t ersebut adalah y = mx + k.

Karena garis ini menyinggung pada lingkaran, maka ada sebuah t it ik yang

koordinat -koordinat nya memenuhi pada persamaan garis maupun persamaan

lingkaran. Sehingga dapat diperoleh

x2 + (mx + k)2 + r2

(1 + m2)x2 + 2mk + k2- r2 = 0

Persamaan ini dipandang sebagai persamaan kuadrat dalam x. Karena garis

singgung dan lingkaran hanya mempunyai t it ik persekut uan, maka persamaan

kuadrat hanya mempunyai sat u harga x, syarat nya adalah diskriminan dari

persamaan t ersebut harus sama dengan nol; sehingga didapat : k =



r

1



m

2 . Jadi persamaan garis singgungnya adalah

y = mx + r

1



m

2 dan

y = mx – r

1



m

2

Dengan cara yang sama dapat dit urunkan bahw a persamaan garis singgung pada

lingkaran (x – a)2 + (y – b)2 = r2 yang sejajar dengan garis y = mx + n adalah

y – b = m(x – a) + r

1



m

2 dan

y – b = m(x – a) - r

1



m

2 .

Cont oh 5

Tent ukan persamaan garis singgung pada lingkaran berikut dan yang mengapit

sudut 60o dengan sumbu-x arah posit if.

a). x2 + y2 = 16

b). x2 + y2 – 4x – 6y – 3 = 0

Pada gambar dibaw ah ini lingkaran x2 + y2 = r2 dan t it ik P(x1 , y1) yangt erlet ak pada

lingkaran. Akan dicari persamaan garis singgung pada lingkaran di t it ik P.

Diambil t it ik Q(x2 , y2) pada lingkaran pula, maka persamaan garis PQ adalah

y – y1 =

1 2

1 2

x

x

y

y





(x – x1).

Karena t it ik P dan Q pada lingkaran, maka berlaku

x22 + y22 = r2 dan x12 + y12 = r2.

Apabila kedua persamaan ini dikurangkan, maka diperoleh

1 2

1 2

x

x

y

y





=

-1 2

1 2

y

y

x

x





Dengan persamaan ini, persamaan garis PQ diat as dapat dit ulis menjadi

y – y1 =

-1 2

1 2

y

y

x

x





(x – x1)

Jika Q mendekat i P sehingga hampir x2 = x1 dan y2 = y1 maka garis PQ berubah

menjadi garis singgung lingkaran di t it ik P, yait u: x1x + y1y = r2.

Jadi persamaan garis singgung lingkaran x2 + y2 = r2 di t it ik (x1,y1) adalah x1x + y1y =

r2.

Dengan cara yang sama dapat dit urunkan bahw a persamaan garis singgung pada

lingkaran (x – a)2 + (y – b)2 = r2 dengan t it ik singgung (x1 , y1) adalah

(x1 – a)(x – a) + (y1 – b)(y – b) = r2.

Cont oh 6

Tent ukan persamaan garis singgung pada lingkaran Q(x2,y2)

P(x1,y1) Y

a). x2 + y2 = 25 di t it ik (4 , -3).

b). x2 + y2 – 4x – 6y – 12 = 0 di t it ik (-1 , 7).

jaw ab: (a) 4x – 3y + 25 dan (b) –3x + 4y – 31 = 0).

Cont oh 7

Diket ahui persamaan lingkaran x2 + y2 + 2x – 19 = 0 dan t it ik B(1 , 6). Tent ukan

t it ik pusat dan jari-jari lingkaran. Selidiki apakah t it ik di bagian dalam, pada, at au

di luar lingkaran. Selanjut nya t ent ukan persamaan garis singgung pada lingkaran

yang melalui t it ik B.

(jaw ab: x – 2y + 11 = 0 dan 2x + y – 8 = 0).

Dengan ilust rasi yang mirip pada pembahasan diat as, dapat dit ent ukan bahw a

Koordinat -koordinat t it ik-t it ik S1 dan S2 memenuhi persamaan xox + yoy = r2. Garis

ini melalui t it ik-t it ik singgung S1 dan S2 dan biasa disebut t ali busur singgung dari

t it ik T. Selanjut nya persamaan ini pula disebut persamaan garis kut ub T(xo , yo)

t erhadap lingkaran x2 + y2 = r2.

Soal-soal

1. Tent kan t it ik pusat dan jari-jari lingkaran x2 + y2 + 4x – 6y + 9 = 0.

2. Tent ukan persamaan lingkaran yang bert it ik pusat di (1 , -2) dan melalui t it ik

(4 , 2).

3. Tent ukan jari-jari lingkaran 9x2 + 9y2 – 54x + 18y + 65 = 0 O

S2(x2,y2)

T(x0,y0)

4. Tent ukan persamaan lingkaran yang melalui O(0 , 0), P(4 , 0), dan Q(0 , 2).

5. Tent ukan persamaan garis singgung lingkaran (x – 1)2 + (y + 1)2 = 4 yang sejajar

dengan garis 5x – 12y + 5 = 0.

6. Tent ukan persamaan garis singgung pada lingkaran x2 + y2 – 2x + 2y – 7 = 0 di

t it ik (1 , 2).

7. Tent ukan persamaan garis kut ub t it ik (2,-1) t erhadap lingkaran (x + 3)2 + (y –

BAB III ELLIPS

Definisi

Ellips adalah himpunan semua t it ik yang jumlah jaraknya t erhadap dua t it ik

t ert ent u t et ap besarnya.

M isalkan t it ik-t it ik api (fokus) F1, F2 pada X dan sumbu F1F2 adalah

sumbu-Y. Jika



F1F2



= 2c maka F1(c , 0) dan F2(-c , 0). M isalkan jumlah jarak yang t et ap it u adalah 2a, dengan a



c. Ambil T(x , y) sebarang t it ik yang memenuhi definisi, yait u

TF

1



TF

2



2

a

Berart i

(

x



c

)

2



y

2 +

(

x



c

)

2



y

2 = 2a

2 2

)

(

x



c



y

= 2a -

(

x



c

)

2



y

2

Set elah kedua ruas dikuadrat kan dan dijabarkan kit a peroleh:

-4cx – 4a2 = -2a

(

x



c

)

2



y

2

Kedua ruas dikuadrat kan lagi dan dijabarkan sehingga diperoleh:

(a2 – c2)x2 + a2y2 = a2(a2 – c2) ………(1)

Karena a



c maka a2 – c2



0; sehingga dapat dit ulis a2 – c2 = b2 Sehingga dari persamaan (1) diat as menjadi:

b2x2 + a2y2 = a2b2

F2 O X

Y

1

2

2

2 2





b

y

a

x

…….(2)

Karena T(x , y) sebarang t it ik yang diambil, maka set iap t it iknya memenuhi

1

2

2

2 2





b

y

a

x

.

Persamaan (2) ini disebut persamaan pusat dari ellips at au persamaan kanonik

dari ellips.

c disebut eksent risit as linear

a

c

disebut eksent risit as numerik, dit ulis e.

Karena a



c maka 0



e =

a

c



1.

Persamaam ellips yang pusat nya P(



,



) dan sumbu-sumbunya sejajar dengan

koordinat adalah

(

)

(

)

1

2

2

2 2









b

y

a

x





Cont oh 1

Tent ukan persamaan ellips yang t it ik-t it ik apinya t erlet ak pada sumbu-X dan

simet ris t erhadap t it ik O sert a sumbu panjangnya 20, eksent risit as numerik e =

5

3

.

(jaw ab:

1

64

100

2 2





y

x

)

O X

Y

Suat u garis lurus dapat memot ong ellips, menyinggung, at au t idak memot ong dan

t idak menyinggung ellips. Dalam hal yang t erakhir garis dan ellips t idak

mempunyai t it ik persekut uan. Selanjut nya akan dicari persamaan garis singgung

yang gradiennya m.

M isalkan persamaan garis yang gradiennya m adalah y = mx + p dan persamaan

ellips ₂

1

2

2 2





b

y

a

x

.

Absis t it ik-t it ik pot ong garis dan ellips diperoleh dari:

1

)

(

2 2

2 2







b

p

mx

a

x

at au

(b2 + a2m2)x2 + 2a2mpx + a2(p2 – b2) = 0

Garis menyinggung ellips jika t it ik-t it ik pot ongnya berimpit . Hal ini t erjadi apabila

persamaan kuadrat diat as mempunyai dua akar yang sama at au apabila

diskriminannya sana dengan nol.

Sehingga D = (2a2mp)2 - 4 (b2 + a2m2) a2(p2 – b2) = 0

Berart i p =



b

2



a

2

m

2

Jadi persamaan garis singgung yang gradiennya m adalah y = mx



b

2



a

2

m

2

Cont oh 2

Carilah persamaan garis singgung pada ellips x2 + 4y2 = 20 yang t egak lurus garis

dengan persamaan 2x – 2y – 13 = 0.

(jaw ab: y = -x



5

Selanjut nya akan dicari persamaan garis singgung pada ellips dengan t it ik

singgung T(x1 , y1).

Y

M isalkan persamaan ellips ₂

1

2 2 2





b

y

a

x

dan P(x2 , y2) suat u t itik pada ellips, maka

berlaku:

1

2 2 2 2 2

2





b

y

a

x

at au b2x22 + a2y22 = a2b2.

Karena T(x1,y1) pada ellips maka berlaku b2x12 + a2y12 = a2b2.

Dari kedua persamaan diat as didapat b2(x12 – x22) = -a2(y12 – y22)

Set elah dijabarkan diperoleh:

2 1 2 1 2 1 2 2 1 2

)

(

)

(

x

x

y

y

y

y

a

x

x

b













Persamaan garis PT adalah

y – y1 =

(

)

)

(

)

(

)

(

₁ 2 1 2 2 1 2 1 1 2 1 2

1

x

x

y

y

a

x

x

b

y

y

atau

x

x

x

x

y

y



















Jika P mendekat i T sedemikian P sangat dekat dengan T sehingga x2 = x1 dan y2 =

y1. Akibat nya PT menjadi garis singgung di t it ik T dan persamaannya adalah:

1

2 1 2

1





b

y

y

a

x

x

.

Unt uk ellips dengan persamaan

(

)

(

₂

)

1

2 2 2









b

y

a

x





, maka persamaan garis

singgung di t it ik (x1 , y1) adalah

(

)(

)

(

1

)(

₂

)

1

2

1













b

y

y

a

x

x









Cont oh 3

Carilah persamaan garis singgung pada ellips

1

24

30

2 2





y

x

di t it ik yang absisnya 5.

Cont oh 4

Carilah persamaan garis singgung pada ellips

1

4

2 2





y

x

dari t it ik T(2 , -1).

Sifat ut ama garis singgung pada ellips sebagai berikut : Garis singgung di suat u t it ik

pada ellips membagi dua sama besar sudut ant ara garis penghubung t it ik it u

dengan t it ik api yang sat u dan perpanjangan garis penghubung t it ik t ersebut

dengan t it ik api lainnya.

Perhat ikan gambar dibaw ah ini.

OO

M isalkan persamaan ellips diat as adalah

1

2 2 2 2





b

y

a

x

dan t it ik-t it ik A1(x’ , y’) dan

koordinat A2(x’’ , y’’) merupakan t it ik-t it ik singgung dari garis-garis singgung ellips

yang melalui t it ik T(x1 , y1) diluar ellips.

Persamaan garis singgung di A1 adalah ₂

1

' 2 '





b

y

y

a

x

x

Karena T pada garis singgung maka

1

2 1 ' 2 1 '





b

y

y

a

x

x

………..(1)

Persamaan garis singgung di A2 adalah ₂

1

'' 2 ''





b

y

y

a

x

x

Karena T pada garis singgung maka

1

2 1 '' 2 1 ''





b

y

y

a

x

x

………..(2)

Dari (1) dan (2) dapat disimpulkan bahw a t it ik-t it ik A1 dan A2 t erlet ak pada garis

dengan persamaan

1

2 1 2

1





b

y

y

a

x

x

.

Persamaan ini disebut persamaan t ali busur singgung dari t it ik T(x1 , y1). A2

A2 T(x1,y1)

Soal-soal

1. Dari t it ik C(10,-8) dibuat garis yang menyinggung ellips

1

16

25

2 2





y

x

. Tent ukan

persamaan t ali busur yang menghubungkan kedua it ik singgung tersebut .

2. Garis x – y – 5 = 0 menyinggung ellips yang t it ik-t it ik apinya F1(-3 , 0) dan F2(3 ,

0). Tent ukan persamaan ellips yang memenuhi persyarat an t ersebut .

3. Tent ukan persamaan garis singgung pada ellips

1

24

30

2 2





y

x

yang sejajar

dengan garis 4x – 2y + 23 = 0.

4. Tent ukan persamaan t ali busur ellips

1

4

8

2 2





y

x

yang dibagi dua sama

panjang oleh t it ik A(2 , 1).

5. Dari t it ik api sebelah kanan ellips

1

20

45

2 2





y

x

dipancarkan sinar yang

mengapit sudut



(t g



= -2) dengan sumbu x posit if. Tent ukan persamaan garis yang dilalui sinar pant ulnya.

6. Tent ukan luas jajar genjang yang dua t it ik sudut nya adalah t it ik-t it ik api dari

ellips

1

5

9

2 2





y

x

dan dua t it ik lainnya berim pit dengan ujung-ujung sumbu

pendek dari ellips.

7. Diket ahui eksent risit as dari ellips adalah e =

5

2

dan jarak dari t it ik M pada

ellips ke salah sat u garis arahnya adalah 20. Tent ukan jarak dari t it ik M ke t it ik

api yang bersesuaian dengan garis arah t ersebut .

8. Suat u ellips menyinggung sumbu-x di t it ik A(3 , 0) dan menyinggung sumbu-y

di di B(0 , -4). Sumbu-sumbu simet rinya sejajar sumbu-sumbu koordinat .

Tent ukan persamaan ellips t ersebut .

9. Dari t it ik P(-16 , 9) dibuat garis singgung pada ellips

1

3

4

2 2





y

x

. Tent ukan

10.Tent ukan persamaan ellips yang sumbunya berimpit dengan

sumbu-sumbu koordinat dan yang menyinggung dua garis 3x – 2y – 20 = 0 dan

BAB IV HIPERBOLA

Definisi: Hiperbola adalah himpunan t it ik-t it ik yang selisih jaraknya t erhadap dua

t it ik t ert ent u t et ap besarnya.

Berdasarkan definisi t ersebut dapat dicari persamaan hiperbola sebagai

berikut .

M isalkan t it ik-t it ik api F1(-c,0), F2(c,0) pada sumbu-x dan sumbu dari F1F2 adalah

sumbu-y. Jika

F

₁

F

₂ = 2c maka F1(c , 0) dan F2(-c , 0).

M isalkan selisih jarak yang t et ap t ersebut adalah 2a, dengan a



c. Ambil T(x , y) sebarang t it ik dari himpunan yang dicari, maka dipenuhi

TF

₁



TF

₂ = 2a

Berart i



x



c



2



y

2 -



x



c



2



y

2 = 2a





2 2

y

c

x





= 2a +



x



c



2



y

2

Set elah kedua ruas dikuadrat kan dan dijabarkan diperoleh

cx – a2 = a



x



c



2



y

2

Jika kedua ruas dikuadrat kan lagi diperoleh

(c2 – a2)x2 – a2y2 = a2(c2 – a2)

Karena a < c maka c2 – a2 > 0 sehingga dapat dit uliskan c2 – a2 = b2 sehingga

didapat :

F2 O X

Y

b2x2 – a2y2 = a2b2

Karena T sebarang t it ik pada him punan, maka set iap t it ik dari himpunan t ersebut

berlaku:

b2x2 – a2y2 = a2b2 at au ₂

1

2

2 2





b

y

a

x

Persamaan diat as disebut persamaan hiperbola.

Tit ik O(0 , 0) sebagai t it ik pusat hiperbola.

Tit ik-t it ik F1 dan F2 disebut t it ik-t it ik api.

Sumbu x dan sumbu y disebut sumbu-sumbu simet ri.

Karena t it ik t it ik pot ong hiperbola dengan sumbu x adalah nyat a, maka

sumbu x disebut sumbu nyat a. Sedangkan t it ik pot ong hiperbola dengan sumbu y

adalah khayal, sehingga sumbu y disebut sumbu khayal. Bilangan e =

a

c

> 1

disebut eksent risit as numerik.

Persamaan hiperbola yang pusat nya P(



,



) dan sumbu-sumbunya sejajar dengan

sumbu-sumbu koordinat diperoleh

(

)

(

)

1

2

2

2 2









b

y

a

x





Tit ik-t it ik pot ong hiperbola ₂

1

2

2 2





b

y

a

x

dengan garis y = mx adalah

F2 P(,) X’

Y’

















2 2 2 2 2

2

,

m

a

b

mab

m

a

b

ab

dan



















2 2 2 2 2

2

,

m

a

b

mab

m

a

b

ab

Jika b2 – a2m2 > 0 maka ada dua t it ik pot ong yang berlainan

Jika b2 – a2m2 < 0 maka t idak ada t it ik pot ong at au t it ik pot ongnya khayal

Jika b2 – a2m2 = 0 maka t it ik pot ongnya di jauh t ak t erhingga.

Dalam hal jika m =



a

b

maka garis y = mx menyinggung hiperbola di jauh

t ak t erhingga. Garis-garis y =



a

b

x disebut asimt ot -asimt ot hiperbola.

Persamaan asimt ot -asimt ot dapat dinyat akan juga sebagai





0

b

y

a

x

dan

0





b

y

a

x

, sehingga susunan asimt ot nya adalah

0

2 2 2 2





b

y

a

x

.

Definisi hiperbola yang lain adalah sebagai berikut : hiperbola adalah t empat

kedudukan t it ik-t it ik yang perbandingan jaraknya t erhadap suat u t it ik dan suat u

garis t ert ent u t et ap besarnya dan perbandingan ini lebih besar dari 1. Selanjut nya

t it ik t ersebut dinamakan t it ik api dan garisnya dinamakan garis arah (direkt rik).

Penjelasannya sebagai berikut .

F2 O X

M isalkan P(x1 , y1) sebarang t it ik pada hiperbola ₂

1

2 2 2





b

y

a

x

.

M aka jarak P t erhadap t it ik api F1(c , 0) adalah d1 =



x

₁



c



2



y

₁2

Dan jarak P t erhadap t it ik api F2(-c , 0) adalah d2 =



x

₁



c



2



y

₁2 Berart i d22 – d12 = 4cx1; sedangkan d2 – d1 = 2a …….. (1)

Jadi d2 + d1 =

a

cx

₁

2

……….(2)

Dari (1) dan (2) diperoleh d1 =















c

a

x

a

c

2

1 dan d2 =















c

a

x

a

c

2 1

Selanjut nya pandang garis-garis x =

c

a

2



M aka d1 =















c

a

x

a

c

2

1 =

a

c

. Jarak t it ik P ke garis x =

c

a

2

M aka d2 =















c

a

x

a

c

2

1 =

a

c

. Jarak t it ik P ke garis x =

-c

a

2

Garis-garis x =

c

a

2



disebut garis-garis arah at au direkt rik dari hiperbola.

Cont oh

Carilah persamaan hiperbola, jika t it ik-t it ik apinya t erlet ak pada sumbu x, simet ris

t erhadap O dan persamaan asimt ot nya y =

x

3

4



sedangkan jarah ant ara kedua

t it ik-t it ik apinya 20.

Carilah persamaan hiperbola, jika t it ik-t it ik apinya t erlet ak pada sumbu x, simet ris

t erhadap O dan persamaan asimt ot nya y =

x

4

3



sedangkan jarak kedua garis

arahnya 12

5

4

.

jaw ab:

1

36

64

2 2





y

x

Selanjut nya dapat dicari persamaan garis singgung pada hiperbola

sebagaimana mencari persamaan garis singgung pada ellips.

Didapat bahw a persamaan garis singgung pada hiperbola ₂

1

2 2 2





b

y

a

x

dengan

koefisien arah m adalah y = mx



a

2

m

2



b

2 .

Jika persamaan hiperbola

(

)

(

₂

)

1

2 2 2









b

y

a

x





, maka garis singgung dengan

koefisien arah m, persamaannya y -





m

(

x





)



a

2

m

2



b

2 .

Persamaan garis singgung parabola ₂

1

2 2 2





b

y

a

x

di t it ik singgung (x1 , y1)

adalah

1

2 1 2

1





b

y

y

a

x

x

.

Jika persamaan hiperbola

(

)

(

₂

)

1

2 2 2









b

y

a

x





, maka persamaan garis

singgung di t it ik (x1 , y1) adalah

F2 P(,) X’

Y’

F1 T(x,y)

1

)

)(

(

)

)(

(

2 1 2

1













b

y

y

a

x

x









Adapun sifat ut ama garis singgung adalah sebagai berikut : garis singgung pada

suat u t it ik pada hiperbola membagi dua sama besar sudut-sudut ant ara garis-garis

yang menghubungkan t it ik singgung dengan t it ik api.

Sepert i pada ellips, t erdapat dua garis singgung melalui sat u t it ik T di luar

ellips, demikian pula pada hiperbola.

Tanpa memperhat ikan let ak t it ik T(x1 , y1), persamaan 1₂

1

2

1





b

y

y

a

x

x

disebut

persamaan garis kut ub dari T t erhadap hiperbola ₂

1

2

2 2





b

y

a

x

.

Jika T di luar hiperbola maka garis kut ub menjadi t ali busur singgung.

Jika T pada hiperbola maka garis kut ub menjadi garis singgung.

Jika T di dalam hiperbola maka garis kut ub berupa garis yang t idak memot ong

hiperbola.

Cont oh

Tent ukan persamaan garis singgung pada hiperbola

1

64

16

2 2





y

x

yang sejajar garis

10x – 3y + 9 = 0.

(jaw ab: 3y = 10x



32)

Cont oh

Dari t it ik C(1 , -10) dibuat garis singgung pada hiperbola

1

32

8

2 2





y

x

. Tent ukan

persamaan garis yang menghubungkan kedua t it ik singgungnya.

Selanjut nya akan dicari syarat agar garis y = mx memot ong garis lengkung

1

2 2 2 2







b

y

a

x

.

Absis-absis t it ik pot ong dapat dicari sebagai berikut :

1

2 2 2 2 2







b

x

m

a

x

at au (b2 – a2m2)x2 = -a2b2.

Berart i x =

2 2 2

m

b

a

ab





.

Jadi garis y = mx dan garis lengkung ₂

1

2 2 2







b

y

a

x

akan

(i) berpot ongan di dua t it ik jika a2m2 – b2 > 0 at au m >

a

b

at au m <

-a

b

(ii) t idak berpot ongan jika a2m2 – b2 < 0 at au

-a

b

< m <

a

b

(iii) menyinggung di jauh t ak hingga jika m =



a

b

.

Persamaan ₂

1

2 2 2







b

y

a

x

adalah persamaan suat u hiperbola yang t idak

memot ong sumbu x t et api memot ong sumbu y di t it ik-t it ik (0 , b) dan (0 , -b).

Berart i sumbu x sumbu khayalnya. Sedangkan persamaan asimt ot -asimt ot nya

adalah

y =

x

a

b

dan y = -

x

a

b

Tit ik-t it ik apinya adalah F1(0 , c) dan F2(0 , -c) dan garis-garis arahnya adalah

y =

c

b

2

dan y =

-c

b

2

Eksent risit as numeriknya adalah e =

b

c

.

Hiperbola-hiperbola ₂

1

2 2 2





b

y

a

x

dan ₂

1

2 2 2







b

y

a

x

pada suat u susunan sumbu

Jika suat u hiperbola a = b, maka hiperbola ini disebut juga hiperbola ort hogonal.

Cont oh

Tent ukan persamaan hiperbola yang t it ik-t it ik apinyat erlet ak pada sumbu y dan

simet ris t erhadap t it ik O yang memenuhi syarat bahw a jarak kedua garis arahnya

7

7

1

dan sumbu 2b = 10.

Jaw ab:

1

25

24

2 2







y

x

Berikut ini adalah t empat kedudukan t it ik-t it ik yang memenuhi syarat -syarat

t ert ent u.

1. Perhat ikan persamaan hiperbola ₂

1

2 2 2





b

y

a

x

dan garis y = mx. Tempat

kedudukan t it ik-t it ik t engah t alibusur-t alibusur hiperbola yang sejajar dengan

garis y = mx adalah y =

x

m

a

b

2 2

; dan persamaan ini m erupakan persamaan

suat u garis t engah hiperbola.

Garis-garis t engah y = mx dan y =

x

m

a

b

2 2

disebut garis-garis t engah sekaw an

dan m1 = m dan m2 =

m

a

b

2 2

disebut arah-arah sekaw an.

2. Persamaan t empat kedudukan t it ik-t it ik pot ong garis-garis singgung pada

hiperbola

1

2 2 2 2





b

y

a

x

yang t egak lurus sesamanya, yait u x2 + y2 = a2 – b2.

Persamaan ini adalah persamaan lingkaran dengan pusat O(0 , 0) dan jari-jari

2 2

b

a



. Selanjut nya lingkaran ini disebut lingkaran ort hopt is dari M onge.

3. Persamaan t empat kedudukan t it ik-t it ik pot ong dari garis-garis singgung pada

hiperbola ₂

1

2 2 2





b

y

a

x

dengan garis-garis yang t egak lurus padanya dan

lingkaran dengan pusat O(0 , 0) dan jari-jari a. Selanjut nya lingkaran ini

disebut lingkaran t it ik kaki.

Lingkaran ort hopt is dari suat u hiperbola ort hogonal berupa lingkaran t it ik dan

garis-garis singgung pada hiperbola it u yang saling t egak lurus adalah asimt

ot-asimt ot nya.

M isalkan t it ik P1(x1 , y1) dan Q1(-x , -y1) ujung-ujung garis t engah hiperbola

1

2 2 2 2





b

y

a

x

. Ujung-ujung garis t engah sekaw annya dapat dicari sebagai berikut .

Persamaan garis singgung di P1(x1 , y1) pada hiperbola

1

2 2 2 2





b

y

a

x

adalah

1

2 1 2

1





b

y

y

a

x

x

.

Berart i gradien garis singgung di P1 adalah m1 =

1 2 1 2

y

a

x

b

Sedangkan gradien P1Q1 adalah m2 =

1 1

x

y

. Jadi m1m2 = ₂

2

a

b

.

Hal ini menunjukkan bahw a garis singgung di P1 sejajar dengan garis t engah yang

sekaw an dengan garis t engah P1Q1.

Persamaan garis t engah yang sekaw an dengan P1Q1 adalah y =

1 2 1 2

y

a

x

b

x.

Absis t it ik-t it ik pot ong garis ini dengan hiperbola dicari sebagai berikut .

b2x2 – a2 ₂ 2 2 2

1 4

2 1

2

x

a

b

y

a

x

b















at au (a2y12 – b2x12)x2 = a2y12. Karena P1(x1 , y1) pada

hiperbola maka didapat x2 =

y

i

b

a

x

atau

b

y

b

a

y

a

1 2 2 1 2 2 2 1 2











.

Berart i t it ik-t it ik pot ongnya khayal yait u





























i

x

a

b

i

y

b

a

dan

i

x

a

b

i

y

b

a

1 1 1

Akan t et api dapat diperiksa bahw a

P

₂













i

x

a

b

i

y

b

a

1

1

,

dan

















1 1

2

,

x

a

b

y

b

a

Q

t erlet ak pada hiperbola sekaw annya ₂

1

2 2 2







b

y

a

x

.

Jika suat u garis t engah t idak memot ong hiperbola, maka yang dimaksud

dengan ujung-ujungnya adalah t it ik-t it ik pot ongnya dengan hiperbola

sekaw annya.

M isalkan OP1 = a1 dan OP2 = a2. M aka diperoleh

1

OP

2 = a1 2

= x1 2

+ y1 2 dan 2 1 2 2 2 1 2 2 2 1 2 2

x

a

b

y

b

a

b

OP







Berart i 2 2 1 2 2 1 2 2 2 1 2 2 1 2 2 1 2 1

a

x

b

y

a

b

y

a

x

b

b

a











= a2 – b2

Jadi 4a12 – 4b12 = 4a2 – 4b2.

Soal-soal

1. Tit ik A(-3 , -5) t erlet ak pada hiperbola yang t it ik apinya F(-2 , -3) dan garis arah

yang bersesuaian dengan t it ik api ini adalah x + 1 = 0. Tent ukan persamaan

hiperbola yang memenuhi persyarat an diat as.

2. Tent ukan nilai p agar garis y =

2

5

x + p menyinggung hiperbola

1

.

36

9

2 2





y

x

3. Tent ukan persamaan garis singgung pada hiperbola

1

5

20

2 2





y

x

yang t egak

4. Tent ukan koordinat t it ik M pada hiperbola

1

18

24

2 2





y

x

yang terdekat ke garis

3x + 2y + 1 = 0.

5. Garis 2x – y – 4 = 0 menyinggung hiperbola yang t it ik-t it ik apinya F1(-3 , 0) dan

F2(3 , 0). Tent ukan persamaan hiperbola t ersebut .

6. Tent ukan luas daerah segit iga yang dibent uk oleh asimt ot -asimt ot hiperbola

1

9

4

2 2





y

x

dan garis 9x + 2y – 24 = 0.

7. Tit ik-t it ik api suat u hiperbola berimpit dengan t it ik-t it ik api ellips

1

9

25

2 2





y

x

.

Jika eksent risit as numerik e = 2, maka tent ukan persamaan hiperbola

t ersebut .

8. Tent ukan persamaan hiperbola yang t it ik-t it ik apinya pada puncak-puncak

ellips

1

64

100

2 2





y

x

dan garis-garis arahnya melalui t it ik-t it ik api dari ellips

t ersebut .

9. Tent ukan persamaan hiperbola yang sumbu-sumbunya berim pit dengan

sumbu koordinat dan menyinggung dua garis 5x – 6y – 16 = 0 dan 13x – 10y –

48 = 0.

10.Tent ukan persamaan t ali busur dari hiperbola

1

4

16

2 2





y

x

yang dibagi dua

BAB V PARABOLA

Definisi: Parabola adalah himpunan t it ik-t it ik yang berjarak sama dari suat u t it ik dan suat u garis t ert ent u. Berdasarkan definisi ini dapat dit ent ukan persamaan parabola sebagai berikut .

M isalkan t it ik yang dimaksud adalah F dan garis yang dimaksud adalah garis g;

perpot ongan garis g dengan sumbu x adalah A; sumbu y dibuat melalui t it ik

t engah AF dan t egak lurus sumbu x. M isalkan jarak

AF



p

. M aka













)

0

,

2

1

p

F

;

dan persamaan garis g adalah x = -

p

2

1

; dan T(x , y) sebarang t it ik pada parabola,

maka berlaku

TF

= jarak T ke garis g at au

2 2

)

2

1

(

x



p



y

= x +

2

1

p

Set elah kedua ruas dikuadrat kan dan dijabarkan diperoleh y2 = 2px.

Persamaan ini disebut dengan persamaan puncak parabola

Tit ik F disebut t it ik api.

Tit ik O disebut puncak parabola

Garis x =

-2

1

p disebut garis arah at au direkt rik

Sumbu x merupakan sumbu simet ri dari parabola p dan disebut paramet er

parabola

T(x,y) g

A O F

Y

Berdasarkan definisi parabola, eksent risit as parabola adalah e = 1.

Dengan menggunakan t ranslasi susunan sumbu, dapat dit ent ukan bahw a

persamaan parabola yang puncaknya P(



,



) dan sumbu simet rinya sejajar sumbu x adalah

(y -



)2 = 2p(x -



).

Cont oh

Tent ukan persamaan parabola yang puncaknya di O, sumbu simet rinya berimpit

dengan sumbu x dan parabolanya t erlet ak di set engah bidang bagian kiri dan

melalui t it ik (-1 , 2).

Jaw ab: y2 = -4x.

Cont oh

Tent ukan persamaan parabola yang t it ik apinya F(7 , 2) dan persamaan garis

arahnya x – 5 = 0.

Jaw ab: y2 – 4y – 4x + 28 = 0.

T(x,y) g

A

F P(,) Y’

X’

y2 = 2px

O Y

Persamaan garis singgung pada parabola dengan gradien m dapat

dit ent ukan sebagai berikut . M isalkan persamaan parabolanya adalah y2 = 2px dan

persamaan garis yang gradiennya m adalah y = mx + n, dengan n paramet er. Absis

t it ik-t it ik pot ong garis dan parabola t ersebut diperoleh dari persamaan (mx + n)2 =

2px, at au dari persamaan m2x2 + (2mn – 2p)x + n2 = 0. Garis akan menyinggung

parabola jika kedua t it ik pot ongnya berimpit at au absis kedua t it ik pot ongnya

sama. Berart i harus t erpenuhi persamaan 4(mn – p)2 – 4m2n2 = 0.

Dari persamaan diat as akhirnya diperoleh n =

m

p

2

.

Jadi persamaan garis singgung pada parabola y2 = 2px dengan gradien m adalah

y = mx +

m

p

2

.

Jika persamaan parabolanya (y -



)2 = 2p(x -



), maka persamaan garis singgung

dengan gradien m adalah (y -



) = m(x -



) +

m

p

2

.

Persamaan garis singgung pada parabola y2 = 2px di t it ik singgung T(x1 , y1) dapat

dit ent ukan sebagai berikut . M isalkan Persamaan garis singgung nya adalah y = mx

+ n. M aka absis t it ik singgungnya dapat diperoleh dari persamaan (mx + n)2 =

2px, at au m2x2 + (2mn – 2p)x + n2 = 0.

Karena hanya ada sat u t it ik singgung maka absisnya adalah

x1 = _{2 2}

2

)

2

2

(

m

mn

p

m

p

mn









………….. (i)

dan ordinat nya adalah

T(x1,y1)

O X

Y

y1 =

m

p

n

m

mn

p

m

(



₂

)





………….. (ii)

Jadi gradien garis singgungnya adalah m =

1

y

p

.

Dari persamaan (i) dan (ii) dan y12 = 2px1, diperoleh n =

2

1

y

.

Jadi persamaan garis singgung pada parabola y2 = 2px di T(x1 , y1) adalah

Y =

2

2

2 1 1

1

1

y

px

y

y

atau

y

x

y

p







at au y1y = p(x + x1).

Jika persamaan parabolanya (y -



)2 = 2p(x -



), m aka persamaan garis singgung di T(x1 , y1) adalah (y1 -



)(y -



) = p(x + x1 - 2



).

Karena gradien garis singgung di T(x1 , y1) adalah

1

y

p

maka gradien garis

normalnya adalah

p

y

₁



. Jadi persamaan garis normal di T(x1 , y1) adalah

y – y1 = 1

(

x

x

₁

)

p

y





.

Persamaan garis singgung pada parabola y2 = 2px yang melalui t it ik T(x1 , y1) di

luar parabola dapat dit ent ukan sebagai berikut . M isalkan t it ik singgungnya S(xo ,

yo). M aka persamaan garis singgung di S adalah yoy = p(x + xo). Karena garis

singgung ini melalui t it ik T(x1 , y1) maka harus memenuhi yoy1 = p(x1 + xo). Karena

(xo , yo) pada parabola, maka yo2 = 2pxo. Akhirnya diperoleh persamaan garis

singgung melalui T di luar parabola.

T O X

Y S

Cont oh

Tent ukan persamaan garis singgung yang melalui t it ik T(-2 , -3) pada parabola y2 =

8x.

Jaw ab: x + 2y + 8 = 0 dan 2x – y + 1 = 0.

Cont oh

Tent ukan t it ik A pada parabola y2 = 8x yang t erdekat dengan garis 2x + 2y – 3 = 0.

Jaw ab: (2 , -4).

M isalkan persamaan parabola y2 = 2px. Tit ik-t it ik S(x1 , y1) dan T(x2 , y2)

merupakan t it ik-t it ik singgung dari garis-garis singgung yang dit arik dari t it ik P(xo ,

yo) di luar parabola.

Persamaan garis singgung di S dan di T bert urut-t urut

y1y = p(x + x1) dan y2y = p(x + x2).

Karena garis-garis singgung t ersebut melalui P maka berlaku

y1yo = p(xo + x1) dan y2yo = p(xo + x2).

Ini berart i t it ik-t it ik S dan T memenuhi persamaan

Yoy = p(x + xo).

Persamaan ini disebut persamaan garis kut ub dari P t erhadap parabola y2 = 2px.

Jika P pada parabola maka garis kut ub menjadi garis singgung.

Jika P di luar parabola maka garis kut ub menjadi t ali busur singgung.

Jika P di dalam parabola maka garis kut ub t idak memot ong parabola.

F T

O X

Adapun sifat ut ama garis singgung adalah sebagai berikut : garis singgung

di suat u t it ik pada parabola membagi dua sama besar sudut ant ara garis yang

menghubungkan t it ik singgung dengan t it ik api dan garis yang melalui t it ik

singgung sejajar dengan sumbu x. (bukt ikan).

Berikut ini akan disajikan beberapa t empat kedudukan t it ik yang

memenuhi syarat t ert ent u.

(1) Tempat kedudukan t it ik-t it ik t engah t alibusur-t alibusur yang sejajar dengan

garis yang gradiennya m adalah y =

m

p

.

(2) Tempat kedudukan t it ik pot ong garis-garis singgung pada parabola yang t egak

lurus sesamanya adalah x = -

2

1

p (persamaan garis arah parabola at au garis

ort hopt is dari M onge).

(3) Tempat kedudukan t it ik-t it ik pot ong garis-garis yang melalui t it ik api dan

t egak lurus garis-garis singgung pada parabola adalah x = 0 at au sumbu y

(garis t it ik kaki).

Soal-soal

1. Tent ukan persamaan parabola yang simet ris t erhadap OX, puncaknya di t it ik

asal, dan melalui t it ik A(9 , 6).

2. Tent ukan persamaan parabola yang puncaknya di O, t erlet ak di t engah-t engah

bidang at as, simet ris t erhadap OY, dan paramet er p =

4

1

.

3. Dari t it ik api parabola y2 = 12x dipancarkan sinar yang membent uk sudut

lancip



(t g



=

4

3

) dengan sumbu x posit if. Tent ukan persamaan garis yang

dilalui sinar pant ul t ersebut .

4. Tent ukan persamaan garis singgung pada parabola y2 = 6x yang t egak lurus

garis y =

3

1

5. Dari t it ik A(-1 , 2) dibuat garis-garis singgung pada parabola y2 = 10x. Tent ukan

persamaan garis yang menghubungkan t it ik-t it ik singgungnya.

6. Tent ukan persamaan parabola yang t it ik apinya F(4 , 3) dan garis arahnya y + 1

= 0.

7. Tent ukan t it ik-t it ik pada parabola yang jaraknya 13 dari t it ik api parabola

t ersebut .

8. Tent ukan t it ik pada parabola y2 = 64x yang t erdekat dengan garis 4x + 3y – 14

= 0.

9. Dari t it ik P(-3 , 12) dibuat garis singgung pada parabola y2 = 10x. Tent ukan

jarak t it ik P ke garis yang menghubungkan t it ik-t it ik singgung t ersebut .

10.Tent ukan persamaan parabola yang puncaknya di A(-2 , -1) dan persamaan

BAB VI

KOORDINAT DAN PERSAM AAN KUTUB

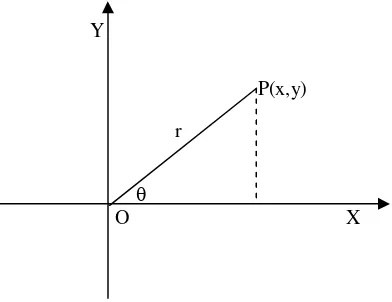
Sebuah t it ik P (selain t it ik kut ub/ t it ik asal) dinyat akan kedudukan oleh t it ik

O ke P dan sudut ant ara garis OP dan sumbu kut ub. Apabila r adalah jarak ant ara

t it ik O dan t it ik P; sedangkan



adalah salah sat u sudut ant ara OP dan sumbu kut ub, maka (r ,



) adalah sepasang koordinat kut ub dari t it ik P dan dit ulis P(r ,



). Selanjut nya r disebut jari-jari penunjuk dari P at au radius vekt or dari P, sedangkan



disebut argumen dari P at au sudut kut ub dari P.

Sepert i halnya dengan sist em koordinat kart esius siku-siku, dapat disusun

persamaan kart esius dengan peubah-peubah x dan y; maka dengan sist em

koordinat kut ub, dapat pula disusun persamaan kut ub dengan peubah-peubah r

dan



; misalnya r = 8 sin



dan r =



cos

1

2



. [image:47.595.183.379.297.448.2]

Cont oh

Gambarlah grafik persamaan kut ub r = 8 sin



.

Cont oh

Gambarlah grafik dari r =



cos

1

2



.

 r

P(x,y)

O Y

Dalam sist em koordinat kut ub, w alaupun ada sepasang koordinat

t ert ent u yang t idak memenuhi suat u persamaan, t et api ini t idak perlu

mengakibat kan bahw a t it ik yang bersangkut an t idak t erlet ak pada grafik

persamaan t ersebut . M isalnya t it ik P(2 ,

2



) t erlet ak pada grafik dan

memenuhi persamaan r =



cos

1

2



. Tet api koordinat P dapat juga dinyat akan

dengan P(-2 ,

2

3



) dan (-2 ,

2

3



) t idak memenuhi persamaan r =



cos

1

2



.

Hubungan koordinat kut ub dan koordinat kart esius dapat diperoleh

sebagai berikut .

r =

x

2



y

2



= arc cos

2 2

y

x

x





= arc sin

2 2

y

x

y



.

Cont oh

Tent ukan koordinat kart esius dari t it ik yang koordinat kut ubnya

adalah













6

,

4



. Tent ukan pula koordinat kut ub dari t it ik yang koordinat

kart esiusnya adalah





3

,

3



.

Cont oh

Tunjukkan dengan jalan menuliskan dalam persamaan kart esius

bahw a grafik persamaan r = sin



adalah sebuah lingkaran; dan bahw a grafik

persamaan r =



2

Soal-soal

1. Sket sa grafik persamaan kut ub r = 6 cos



. Berupa apakah grafiknya?

2. Sket sa grafik persamaan kut ub r =



cos

5

. Berupa apakah grafiknya?

3. Ubahlah persamaan kart esius (x – 2)2 + y2 = 4 menjadi persamaan kut ub.

4. Ubahlah persamaan kut ub r =



sin

2

1

1

DAFTAR KEPUSTAKAAN

M oehart i Hadiw idjojo, Ilmu Ukur Analit ik Bidang, Yogyakart a: FPM IPA-IKIP Yogyakart a, 1974.

Purcell, Edw in J (Pent erjemah: Raw uh, Bana Kart asasmit a), Kalkulus Dan Geomet ri Analit is Jilid I, Jakart a: Erlangga, 1984.