BAB IV APLIKASI INTEGRAL TERTENTU

BAB IV

APLIKASI INTEGRAL TERTENTU

Standar Kompetensi

Setelah mempelajari pokok bahasan ini diharapkan mahasiswa dapat memahami penggunaan integral tertentu dalam masalah-masalah praktis.

Kompetensi Dasar

1. Mahasiswa dapat menentukan luas suatu luasan dengan menggunakan integral tertentu.

2. Mahasiswa dapat menentukan volume benda putar dengan menggunakan integral tertentu.

3. Mahasiswa dapat menentukan luas permukaan benda dengan menggunakan integral tertentu.

4. Mahasiswa dapat menentukan panjang busur dengan menggunakan integral tertentu.

Bab V dalam buku ini membahas aplikasi integral tertentu untuk: (1) luas suatu luasan, (2) volume benda putar (3) luas permukaan, dan (4) menentukan panjang busur.

a. Daerah antara Kurva dan Sumbu Koordinat. Perhatikan gambar daerah rata dibawah ini

R adalah

bidang datar yang dibatasi oleh grafik-grafik yf(x),xa,xb,dan y 0

Dengan menggunakan integral tertentu luas luasan R dinyatakan dengan

dx x f R

A

b

a



 ( )

) (

Jika luasan terletak dibawah sumbu X maka integral tertentu di atas bernilai negatif, karena luas daerah tidak mungkin bilangan negatif maka nilai integral tersebut dimutlakkan. Sehingga luas luasan daerah negatif dinyatakan dalam bentuk





 



b

a b

a

dx x f dx x f R

A( ) ( ) ( )

Untuk menghitung luas luasan dengan integral tertentu dapat diikuti langkah-langkah sebagai berikut :

a) Gambar daerah yang bersangkutan

b) Potong daerah menjadi jalur-jalur dan beri nomor pada satu jalur tertentu c) Hampiri luas jalur tertentu tersebut dengan luas persegi panjang

d) Jumlahkan luas jalur-jalur pada daerah tersebut

e) Ambil limit dari jumlah diatas dengan lebar jalur menuju 0, maka diperoleh integral tertentu.

1. Segitiga ABC terletak pada XOY, titik-titik sudutnya dinyatakan dalam koordinat Cartesius. Titik A(0,0), B(3,0) dan C(3,7). Dengan menggunakan integral tertentu tentukan luas segitiga ABC.

Persamaan garis AC dapat dinyatakan dengan rumus

A c A c A A x x y y x x y y      Diperoleh persamaan 0 3 0 7 0      x y 3 7 7

3y xatau y x

Sehingga luas yang dicari dinyatakan denA R f x dx b a



 ( ) ) ( 5 , 10 9 6 7 6 7 3 7 3 0 2 3 0               





xdx x

2. Tentukan luas luasan yang dibatasi oleh kurva _{y 4 x}2 _{dan sumbu-sumbu}

koordinat. Jawab

3. Tentukan luas luasan yang dibatasi oleh kurva _xy2 _{dan garis x4}

Selanjutnya, perhatikan gambar luasan berikut ini :

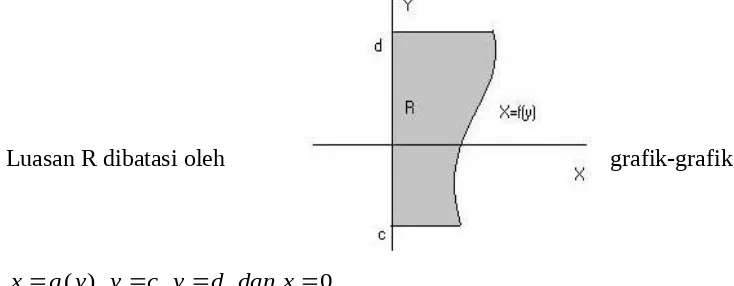
Luasan R dibatasi oleh grafik-grafik

0 ,

, ),

(   

g y y c y d danx

x _.

Dengan integral tertentu luas luasan R yang berada disebelah kanan sumbu x

dinyatakan dalam bentuk A R g y dy

d

c



 ( )

) (

Jika gambar terletak disebelah kiri sumbu x maka integral tertentu di atas bernilai negatif, karena luas daerah tidak mungkin bilangan negatif maka nilai integral tersebut dimutlakkan, sehingga diperoleh:





 



d

c d

c

dy y g dx y g R

A( ) ( ) ( )

Perhatikan contoh-contoh berikut:

1. Segitiga ABC terletak pada XOY, titik-titik sudutnya dinyatakan dalam koordinat Cartesius. Titik A(0,0), B(-3,0) dan C(-3,-7). Dengan menggunakan integral tertentu tentukan luas segitiga ABC.

2. Tentukan luas luasan yang dibatasi oleh kurva _{y 4 x}2 _{dan sumbu-sumbu}

koordinat.

3. Tentukan luas luasan yang dibatasi oleh kurva _xy2 _{dan garis x4}

[image:4.595.111.478.158.301.2]

Perhatikan kurva-kurva yf(x)_dan yg(x) _dengan f(x)g(x)_{pada selang}



a,b



, seperti gambar berikut :



f x g x



x

A  

 ( ) ( )

Sehingga luas luasannya dinyatakan dengan:





 b

a

dx x g x f R

A( ) ( ( ) ( ))

Rumus di atas berlaku untuk luasan di atas sumbu x, jika luasannya disebelah kanan sumbu y, maka luas luasan yang dibatasi oleh dua kurva dinyatakan dengan





 d

c

dy y g y f R

A( ) ( ( ) ( ))

Soal-soal

1. Hitung luas daerah yang dibatasi oleh kurva y = x2 2 dan

y = 2x2 x 4

2. Hitung luas daerah yang dibatasi oleh kurva-kurva y = x, y = 2x dan y = 5 – x

3. Hitung luas daerah yang dibatasi oleh kurva y = x dan y = -x + 6

4. Gambarlah daerah R yang dibatasi oleh kurva-kurva y = x + 6, y = x3 _dan

4.2 Volume Benda Putar

a. Pemutaran mengelilingi sumbu X

b. Pemutaran mengelilingi sumbu Y

1. V x dy

d

c



 2

2. V x x dy

d

c

)

( 2

Benda putar yang sederhana dapat kita ambil contoh adalah tabung dengan besar volume adalah hasilkali luas alas ( luas lingkaran ) dan tinggi tabung. Volume dari benda putar secara umum dapat dihitung dari hasilkali antara luas alas dan tinggi. Bila luas alas dinyatakan dengan A(x) dan tinggi benda putar adalah panjang selang [ a,b ] maka volume benda putar dapat dihitung menggunakan integral tentu sebagai berikut :

dx x A V

b

a



 ( )

Untuk mendapatkan volume benda putar yang terjadi karena suatu daerah diputar terhadap suatu sumbu, dilakukan dengan menggunakan dua buah metode yaitu metode cakram dan kulit tabung.

Metode Cakram

Misal daerah dibatasi oleh yf(x),y0,x1,danxb diputar dengan sumbu

putar sumbu x. Volume benda pejal/padat yang terjadi dapat dihitung dengan memandang bahwa volume benda padat tersebut merupakan jumlah tak berhingga cakram yang berpusat di titik-titik pada selang



a,b



_.

Misal pusat cakram



x0,0



dan jari-jari rf

 

x0 . Maka luas cakram dinyatakan :

 

 

0 2 0 f x

x A 

Oleh karena itu, volume benda putar :









b

a

dx x f

V _{( )} 2

Sedang bila grafik fungsi dinyatakan dengan xg(y), x0, ycdan y d

diputar mengelilingi sumbu Y maka volume benda putar :







 d c dy y g

V _{( )} 2



Bila daerah yang dibatasi oleh y f

 

x 0 _, yg

 

x 0,f(x)g(x)_untuk

setiap x



a,b



,xadan xb _{diputar dengan sumbu putar sumbu X maka}

volume:







  b a dx x g x f

V 2( ) 2( )



Bila daerah yang dibatasi oleh xf

 

y 0,xg

 

y 0, f(y)g(y) untuk setiap



c d



y cdan y d

y , ,   _{diputar dengan sumbu putar sumbu Y maka volume :}







  d c dy y g y f

V _ 2( ) 2( )

Contoh :

1. Hitung volume benda putar bila luasan yang dibatasi oleh : _{y x}2 _dan

x

y2 _8 _{diputar mengelilingi}

a. sumbu X. b. sumbu Y Jawab :

Kedua kurva berpotongan di titik ( 0,2 ) dan ( 2,4 ). a. Pada selang



_0,2



_{, 8x x}2 _.

Volume benda diputar mengelilingi sumbu x dinyatakan oleh





 

  5 48 8 2 0 2 2 2        _





x x dx

V

b. Pada selang





8 ,

4 ,

0 y y2

 

  5 48 8 2 0 2 2 2                





y y dy

V

2. Hitung volume benda putar bila luasan yang dibatasi oleh kurva-kurva :

x y x

y 2 2, 

dan sumbuY bila diputar mengelilingi garis y 2

Jawab :

Kedua kurva berpotongan di



 1,1



dan



2,2



. Pada selang



 1,0



berlaku 2 x2 x.

Jarak kurva y2 x2, y x _{terhadap sumbu putar (garis y = -2) dapat}

dipandang sebagai jari-jari dari cakram, berturut-turut adalah



4 x



dan



2 x



_.

Sehingga volume benda putarnya adalah:













  5 36 2 4 0 1 2 2

2 _{  }

 



 dx x x V

Metode Kulit Tabung

Metode kulit tabung sebagai alternatif lain dalam perhitungan volume benda putar yang mungkin lebih mudah diterapkan bila kita bandingkan dengan metode cakram. Benda putar yang terjadi dapat dipandang sebagai tabung dengan jari-jari kulit luar dan dalamnya berbeda, maka volume yang akan dihitung adalah volume dari kulit tabung. Untuk lebih memperjelas kita lihat uraian berikut.

Pandang tabung dengan jari-jari kulit dalam dan kulit luar berturut-turut

1

r dan r2 , tinggi tabung h. Maka volume kulit tabung adalah :



r r



h rh r

V    

 2 1 2



rata rata jari jari



r r r

r r r

dengan 2  1   _,  _{, 2}  ₁ 

Bila daerah yang dibatasi oleh yf(x), y0,xa,xb _{diputar mengelilingi}

sumbu Y maka kita dapat memandang bahwa jari-jari r xdanrx_dan

tinggi tabung hf(x) _{Oleh karena itu volume benda putar yang terjadi adalah}

 

xdx xf V

b

a



 2

Misal daerah dibatasi oleh kurva

 

x y g

 

x f x g x x



a b



x adanx b f

y ,  , ( ) ( ),  , ,   diputar mengelilingi

sumbu Y. Maka volume benda putar



f x g x



dx

x V

b

a





 2 ( ) ( )

Bila daerah dibatasi oleh grafik yang dinyatakan dengan

d y c y x y f

x ( ), 0,  ,  _{diputar mengelilingi sumbu X, maka volume =}



f y



dy

y V

d

c



 2 ( )

Sedang untuk daerah yang dibatasi oleh

 

y x g

 

y f y g y y



c d



dan y cdany d f

x ,  , ( ) ( ),  , ,   _diputar

mengelilingi sumbu X. Maka volume benda putar yang didapat dinyatakan dengan



f y g y



dx

y V

d

c





 2 ( ) ( )

Contoh :

1. Hitung volume benda putar bila daerah yang terletak di kuadran pertama dibawah parabola

Jawab

2

2 x

y  _{dan di atas parabola yx}2 _{diputar mengelilingi sumbu Y.}











   





x x x dx

V 1

Bila kita gunakan metode cakram, maka daerah kita bagi menjadi dua bagian yaitu : pada selang 0y1 _dibatasi x 2 y_{dan sumbu Y sedang pada} selang dibatasi 1y2

dan sumbu Y. Oleh karena itu volume =

 









   





y dx



y dy

V

2 2

1 1

0 2

2

2. Hitung volume benda putar bila daerah D yang dibatasi oleh _{y1 x}2 _,

sumbu X dan sumbu Y bila diputar mengelilingi garis x = 1 Jawab

Misal di ambil sembarang nilai x pada daerah D maka didapatkan tinggi

benda pejal,



_{1 x}2



_{dan jari-jari ( jarak x terhadap sumbu putar / garis x =}

1 ), ( 1 + x ). Oleh karena itu, volume benda putar :













6 5 1

1

2 2

0

1

 









dx x x V