Matematika ekonomi

Pemecahan untuk mencari titik ekuilibrium sebelumnya adalah relative sederhana. Bila semakin banyak barang yang dimasukkan kedalam model, maka penyelesaian dengan rumus tsb menjadi tidak praktis. Metoda yang lebih baik untuk pemecahan persamaan simultan dengan beberapa variable adalah menggunakan aljabar matriks.

Aljabar matriks membantu kita : Aljabar matriks membantu kita :

a. Memberikan sistem persamaan yang ringkas. b. Pemecahannya melalui determinan.

Pengertian :

Matriks adalah susunan/daftar/array dari suatu angka2 yang mempunyai ikatan berdasar baris atau kolom dan yang mempunyai kegunaan tertentu.

Susunan Baris : angka2 diurutkan secara horizontal (ke arah kanan – kiri )

Susunan Kolom : angka2 diurutkan secara vertikal ( dari Susunan Kolom : angka2 diurutkan secara vertikal ( dari

atas – bawah )

Ikatan : menunjukkan hubungan secara berturut. Misal, krn matriks merpkan nilai paramater dari suatu

persamaan.

Kegunaan : untuk menyederhanakan, memudahkan

Perhatikan matriks A berikut :

a₁₁ a₁₂ a₁₃ 1 3 5

A : a₂₁ a₂₂ a₂₃ : 0 2 7

a₃₁ a₃₂ a₃₃ 6 4 8

Pengertian baris (raw) dan kolom (lajur/coloumn) :

a₁₃ : menunjukkan element (unsur) matriks A yang terletak pada baris ke 1 dan kolom ke 3, 5 terletak pada baris ke 1 dan kolom ke 3, 5 a₂₁ : menunjukkan element (unsur) matriks A yang

terletak pada baris ke 2 dan kolom ke 1, 0 Analog :

4.1. Matriks dan vektor

Secara umum sistem dengan m persamaan linear dan n variabel (x₁, x₂, …… , x_n) dapat disusun dalam bentuk :

a₁₁x₁ + a₁₂x₂ + ….. + a_1nx_n = d₁ (4.1) a₂₁x₁ + a₂₂x₂ + ….. + a_2nx_n = d₂

: : : = :

a_m1x₁ + a_m2x₂ + ….. + a_mnx_n = d_m a_m1x₁ + a_m2x₂ + ….. + a_mnx_n = d_m

Dalam sistem persamaan (4.1) terdapat 3 macam bahan pokok, yaitu :

1. Himpunan koefisien a_ij,

a₁₁ a₁₂ a₁₃ x₁ d₁ (4.2) A : a₂₁ a₂₂ a₂₃ x : x₂ d : d₂

: : : : :

a₃₁ a₃₂ a₃₃ x_n d_n

Contoh :

6x₁ + 3x₂ + x₃ = 22 (4.3) x₁ + 4x₂ – 2x₃ = 12

4x₁₁ – x₂₂ + 5x₃₃ = 10

Dapat ditulis

6 3 1 x₁ 22

(4.4) A : 1 4 – 2 x : x₂ d : 12

4 – 1 5 x_n 10

Vektor sebagai matriks khusus

Jumlah baris dan kolom dalam suatu matriks menunjukkan dimensi dari matriks.

Sebuah matriks yang memiliki banyaknya baris sama dengan banyaknya kolom, disebut matriks kuadrat (square matrix).

Matriks yang berisi satu kolom, disebut vektor kolom. Matriks yang berisi satu baris, disebut vektor baris, Matriks yang berisi satu baris, disebut vektor baris,

vektor baris menggunakan simbol x’ = [ x₁ x₂ …. X_n ]

Dengan menggunakan matriks dalam (4.4) kita dapat me-nyatakan persamaan (4.3) menjadi

4.2. Operasi dengan matriks

1. Persamaan (equality).

2. Penjumlahan dan pengurangan matriks.

3. Perkalian bilangan (scalar multiplication)

4. Perkalian matriks

4.3. Beberapa jenis matriks

4.3. Beberapa jenis matriks

1. Matriks nol

6. Skalar

2. Matriks identitas

7. Vektor

3. Matriks diagonal

8. Matriks non singular

4. Matriks skalar

9. Matriks singular

4.6. Transpose dan inverse

Transpose suatu matriks A dapat ditulis AT _{atau A’.}

Diten-tukan dengan merubah elemen tiap baris

matriks A men-jadi kolom2 matriks A’ atau sebaliknya.

a₁₁ a₁₂ a₁₃ a₁₁ a₂₁ a₃₁ A : a₂₁ a₂₂ a₂₃ A’ : a₂₁ a₂₂ a₂₃

a a a a a a

21 22 23 21 22 23

a₃₁ a₃₂ a₃₃ a₃₁ a₃₂ a₃₃ Atau

4 6 B’ : 4 2 – 4

B : 2 0 6 0 5

Sifat-sifat transpose

Sifat – sifat berikut meripakan ciri dari transpose : 1. (A’)’ = A

2. (A + B)’ = A’ + B’ 3. (AB)’ = B’A’

Inverse dan sifat-sifatnya Inverse dan sifat-sifatnya

Inverse matriks A ditunjukkan dengan simbol A–1_{, hanya}

dapat ditentukan bila A adalah matriks kuadrat, dimana inverse adalah matriks yang memenuhi kondisi

Beberapa yang perlu diperhatikan :

1. Tidak semua matriks kuadrat mempunyai inverse. Bila matriks kua-drat A dapat diinverse (dibalik), maka A dis non – singular. Bila A tdk bisa diinverse disebut matriks singular.

2. A dan A–1 _{merupakan inverse satu sama lain.}

3. Bila A adl n x n, maka A–1 _{juga harus n x n. Matriks identitas yang}

diperoleh juga berdimensi n x n.

4. Bila suatu matriks mempunyai inverse, maka hanya memp satu inverse matriks. Bila A–1 _{adalah B, maka AB = BA = I}

inverse matriks. Bila A–1 _{adalah B, maka AB = BA = I}

terdapat matriks lain C, shg AC = CA = I. dengan mengalikan bagian AB = I dengan C , kita peroleh CAB = CI

karena CA = I maka IB = C atau B = C

5. A.A–1 _{= A}–1_{.A = I . Sebenarnya menyatakan bahwa kedua hubungan}

Matriks inverse dan penyelesaian sistem persamaan linear

Penggunaan konsep matriks inverse dalam penyelesaian suatu sistem persamaan linear adalah langsung dan cepat. Dari sistem persama-an linear (4.3) dapat ditulis dalam bentuk matriks sebagai berikut :

(4.17) A x = d

(3x3) (3x1) (3x1)

sekarang bila terdapat matriks inverse A–1 _{perkalian kedua bagian}

sekarang bila terdapat matriks inverse A–1 _{perkalian kedua bagian}

persamaan (4.17) dengan A–1 _{akan menghasilkan}

A–1 _{Ax = A}–1_d

atau

(4.18) x = A–1 _d

Penyelesaian (perhitungan akan dibahas dalam bab berikutnya)

1 18 – 16 – 16

A–1 _{= ---- – 13 26 13}

52 – 17 18 21

x₁ 1 18 – 16 – 10 22 2

x = ---- – 13 26 13 12 = 3

x₂ = ---- – 13 26 13 12 = 3

x₃ 52 – 17 18 21 10 1



Integral dikenal dua macam pengertian

yaitu :

a.

Integral tak tentu (

Indefinite Integral

)

b.

Integral tentu (

Definite Intergral

)



Suatu konsep yang berhubungan dengan

proses penemuan suatu fungsi asal, apabila

turunan atau derivatif dari fungsinya

diketahui



Bentuk umum integral tak tentu:



Rule 1

: Power rule



Rule 1’

: generalised



Rule 1’

: generalised

“power rule”/

substitution rule:



( )



'( )



( )



1

1

1

n

n

f x

f x

f x dx

C

n

n







 

2

4 3

3

3

1

2

(2

2)

(2

2) (2)

4

dx

x c

x dx

x

c

x

x

dx

C























Latihan



















dx

x

dx

x

dx

x

4 3 3

1



Rule 2

: Integral of a constant multiple :

c x c

x dx

c x c

x dx

 

 

 



 

 

 



 

6 1

0 1 6 6

1 0

1 1

1 0 1 0



Rule 3

: Integral of a sum:



Contoh

:

2

2 2

2 2 2 3

(3 2 ) 3 2 3

1 3

3 3 3

2 2

3 2

(3 2 ) 3 2

2 3

x dx dx xdx x x c

xdx xdx x x

x x dx xdx x dx x x c

     

 

  _{ } 

 

     



































dx

x

e

dx

x

x

x

)

1

(

)

1

(

3



Rule 4

: Exponential rule:



Rule 4’

: Generalised

4 4

2 5

2 5

1

2 5

2

2

x

x x

e dx

e

c

e

e

dx

c

e

c



 

 



 







Latihan















dx

e

dx

e

x

)



Rule 5

:“aturan

logaritma:

1

1

ln

1

dx

x C

x

















1



1

2

x dx

2

dx

2.ln

x c

x











Rule 6 : Integral Perkalian

dx

x

f

k

dx

x

kf

(

)





(

)





Contoh:

dx

x

f

dx

x

f

c

x

c

x

dx

x

dx

x

)

(

)

(

3

2

)

3

(

2

2

2

3 3 2 2



























Latihan:







dx



x

x

e

x

1

3

)

5

c x x dx x x dx x x dx x x cari           2 4 3 2 2 2 ) 2 2 ( ) 1 ( 2 ) 1 ( 2

Cara Langsung :

Cara Subtitusi

Dengan cara subtitusi ; misal u = x2 _{+ 1, maka}

du/dx =2x atau dx=du/2x













dx

e

dx

x

x

x 3 2

9 3

2

8

.

2

)

2

(

6

.

 Consider two continuous functions u=f(x) and v=g(x), then,

[ ( ). ( )] ( ). '( ) '( ). ( )

( ) ( )

Let us assume that and Then,

d

f x g x f x g x f x g x dx

u f x v g x

 

 

 

( ) . .

. .

. .

Let us integrate both sides

Rearranging:

d uv u dv du v

uv u dv v du

u dv uv v du

 

 

 





3

3,

0,

Using integration by parts, find

dx

u

dv

dx

du

v

x











0,

.

.

3.

3

.0

3

du

v

x

u dv

uv

v du

dx

x

x

x c





















2

(2

3)(2 )

(2

3),

2

2,

2

.

.

Using integration by parts, find

x

x

u

x

dv

x

du

v

x

x

u dv

uv

v du



























2 2

3 2 2

3 2 3 3 2

.

.

(2

3).(2 )

(2

3)(

)

.2

(2

3

) 2

2

4

2

3

3

3

3

u dv

uv

v du

x

x

x

x

x

x

x

x

x

x

x

x

x

c







































2

2 3 2 3 2

(2

3)(2 )

(4

6 )

4

6

4

4

6

3

3

2

3

Verification

x

x

x

x dx

x dx

x dx

x

x

c

x

x

c















 











Integral dari suatu fungsi yang nilai-nilai variabel

bebasnya memiliki batas tertentu



Integral tertentu sering digunakan untuk

menghitung luas area yang terletak diantara

kurva y=f(x) dan sumbu x dalam suatu rentangan

wilayah yang dibatasi oleh x=a dan x=b

wilayah yang dibatasi oleh x=a dan x=b



Proses pencarian luas suatu area yang

batas-batas atau limit dari area tersebut sudah

ditentukan



Dalam integral tak tentu kita temukan bahwa :

c

x

F

dx

x

f







Untuk mengetahui hasil integrasi teresbut untuk

suatu rentangan wilayah tertentu, katakanlah

antara x = a dan x = b, dimana a<b, maka

persamaan diatas menjadi :



[F(b)+c] – [F(a)+c] = F(b) – F(a)

F(b) – F(a) : hasil integral tertentu dari f(x) antara a



F(b) – F(a) : hasil integral tertentu dari f(x) antara a

dan b.



Secara lengkap persamaan pertama tadi dapat

dituliskan menjadi :







b   

a

b

a F b F a x

F dx

x



Notasi

f(x)dx dibaca integral f(x) untuk rentangan

wilayah x dari a ke b. selanjutnya, mengingat a<b, a

dinamakan batas bawah integrasi (lower limit

integration) sedangkan b disebut batas atas

integrasi (upper limit integration)



b

a

 Jika suatu fungsi f(x) adalah kontinu dalam suatu

interval, maka fungsi tersebut mempunyai integral (antiderivatif) dalam intervalnya dan lebih lanjut jika F(x) adalah integral dari f(x) maka untuk 2 titik a dan b dalam interval kita dapatkan :

b dalam interval kita dapatkan :







b

a

a

F

b

F

dx

x

      _             5 5 5 2 5 5 4 4 5 2

4 _{(2) 5(618,6) 3093}

LIMIT



Limit merupakan konsep dasar yang penting

dalam cabang matematika yang dikenal

dengan kalkulus



Kita dapat mengetahui seberapa jauh suatu



Kita dapat mengetahui seberapa jauh suatu

fungsi akan berkembang apabila variabel di

dalam fungsi tersebut terus menerus

PERNYATAAN PADA LIMIT



Limit fungsi f(x) untuk mendekati a adalah L, dimana a

dan L masing-masing adalah bilangan.



Artinya jika x bertambah secara terus menerus hingga

mendekati a, maka nilai fungsi f(x) pun akan bertambah

L

x

f

a

x

(

)



lim

mendekati a, maka nilai fungsi f(x) pun akan bertambah

hingga mendekati L

KAIDAH-KAIDAH LIMIT

8 2 lim : lim ) ( . 1 3 3

2  

     x a n a x n x contoh a x x x f y 5 5 lim : lim . 2 2      x a x contoh k k k

LIMIT SUATU

PENJUMLAHAN/PENGURANGAN



Jumlah selisih dari limit fungsi-fungsinya



(

)

(

)



lim

(

)

lim

(

)

lim

)

(

)

(











  

Contoh

x

g

x

f

x

g

x

f

x

g

x

f

y

a x a x a x

17

8

9

)

(

lim

)

2

1

(

lim

)

(

)

2

1

(

3 2 2 2 3 2





















x

x

LIMIT DARI SUATU PEMBAGIAN



Pembagian dari limit fungsi-fungsinya dengan syarat

limit fungsi pembagi (penyebut)

) ( lim ) ( ) (  x f x g x f y  11 ) 1 ( ) 11 )( 1 ( ) 5 ( lim ) 5 )( 5 ( lim ) 5 ( lim ) 25 ( lim ) 5 ( ) 25 ( lim 5 25 : ) ( lim ) ( lim lim 6 6 6 2 6 2 6 2                        x x x x x x x x x y contoh x g x f x x x x x a x a x a x 0 ) ( lim 

a g x x

LIMIT 2 FUNGSI



Dua fungsi yang serupa mempunyai limit yang sama f(x)

= g(x)

L

x

f





(

)

lim

g

x



L



(

)

lim

juga

L

x

f

a

x

(

)



lim

g

x

L

a

x

(

)



lim

SOAL LIMIT

    x x x x 2 4 2 lim . 2 lim . 1 2 3 3 lim ) 3 ( ) 4 2 ( . 3      x x x y 16 2

x x2

      

 _{( 4)}

DIFERENSIAL



Pada dasarnya merupakan proses penarikan

limit atas suatu koefisien diferensi dalam hal

tambahan variabel bebasnya mendekati nol.



Hasil yang diperoleh dari proses diferensiasi

dinamakan turunan (y’) atau derivatif

     

PERHITUNGAN DIFERENSIAL

 Mencari laju perubahan suatu fungsi.

 Dalam ekonomi, diferensial dapat digunakan untuk memecahkan soal

bagaimana meminimalkan biaya dan memaksimalkan laba.

 Analisis dalam ekonomi adalah terutama analisa mengenai perubahan.

 Analisis marginal adalah analisis mengenai laju perubahan marginal yaitu

laju perubahan sesaat yang tak lain daripada hasil bagi diferensial atau turunan pertama dari fungsi-fungsi yang bersangkutan, misal fungsi permintaan, penawaran, produksi, biaya, pendapatan, konsumsi, tabungan, permintaan, penawaran, produksi, biaya, pendapatan, konsumsi, tabungan, harga, laba, dan lain-lain.

 Laju perubahan sesaat di suatu titik X dinamakan hasil bagi diferensial atau

turunan fungsi yang dilambangkan :

atau didefinisikan dengan suatu limit, yaitu



Jika

f

(

x

) =

y,

maka turunannya dituliskan juga

'

,

0

lim

y

atau

dx

dy

x

y

x









KAIDAH-KAIDAH DIFERENSIAL

A. Turunan Fungsi Aljabar 1. Turunan dari fungsi

 



n1

2. Turunan Suatu Konstanta

3. Turunan Suatu Jumlah

 

0 0 10 0          dx dy e y dx dy y contoh dx c d c y







_{ }  

 u v d u v u' v'

y

Turunan Suatu Jumlah





5.Turunan Suatu Hasil Bagi

 











3









2

 

2 3 2 2

3

2

1

4

3

3

2

'

'























x

x

x

x

x

dy

maka

x

x

x

y

contoh

v

uv

vu

dx

uv

d

v

u

y











 









6.Turunan Fungsi berantai (fungsi komposit)

Yaitu fungsi dari fungsi, misal y = F ( u ) sedang u = f ( x )

Sehingga y adalah juga fungsi dari x

 





dx

du

du

dy

dx

dy

x

f

F

y











x



y

contoh

3

3 2









 

 





 



Turunan Fungsi Kebalikan (invers)

Y = f(x) x = g (y) merupakan fungsi kebalikan

( x = f

-1

(y))

Rumus : dy/dx = 1/ dy/dx or dx/dy = 1/dy/dx

Contoh :

Contoh :



Turunan Fungsi Logaritma dengan bilangan 10

Y=

10

log x

Dy/dx = 1/x log e = 1/xln 10

Contoh :

y = log 8x

y= log 8 + log x

dy/dx = 1/x log e dy/dx = 1/x log e

Y = log 2x

3

y = log 4x

2

y = log 4x

2

y = log u

dy/dx = 1/u log e dy/dx

Contoh :



Turunan fungsi logaritma dengan bilangan pokok e

Y =

e

log x

dy/dx = 1/x

e

log e menjadi 1/x ln e = 1/x(1)

Contoh ;

Y = lnx

3

dy/dx = 3 ln x = 3/x

Y = ln u menjadi dy/dx = 1/u .du/dx/ ln e

Contoh :

Y = ln (4x-3) dy/dx = 1/(4x-3) . 4

Y = ln (4x-3) dy/dx = 1/(4x-3) . 4



Turunan fungsi logaritma dengan bilangan pokok

sembarang



Fungsi peubah lebih dari dari dua

Turunan Parsial



Merupakan

perluasan

lebih

lanjut

dari

perhitungan

dengan

konsep

penurunan

dihubungkan

langsung

dengan

fungsi

multivariat (banyak peubah)



Z = f(xy) differensial parsial fx ; fy



Z = f(xy) differensial parsial fx ; fy



Partial derivatives dz/dx ; dz/dy



Y = f(x

₁

, x

₂

, x

₃

)

Diferensial total



diferensial dy dari y = f(x,z) dinamakan

diferensial total yang besarnya dy = dy/dx .

dx + dy/dz.dz

Contoh :



Z= x

2

+xy – y

2 

Z= x

2

+xy – y

2

Turunan Fungsi Implisit

 F(x,y) = 0

 Df/dx.dx + df/dy.dy = o menjadi dy/dx = -df/dx/dfdy

 Contoh :

2x3 _{– xy}2 _{+ y}2 _{+12 df/dx.dx + df/dy.dy = o}

(6x2_{-2y) + (-2x + 2y) dy/dx = - 6x}2_{-2y/-2x + 2y}

X2 _{– xy -2y}2 _{= 0}

Fungsi dari fungsi

Jika Z = f (x,y) dimana x = x(t) dan y = y(t) maka total derivatif menjadi : dz = dz/dx.dx + dz/dy.dy dikatakan total deferensial

Dz/dt = dz/dx . Dx/dt + dz/dy.dy/dt Contoh :

Z = 5x +2y dimana x = t2 _{+3 dan y = 5t}3 _{+ 4}

Dz/dx = 5 dz/dy = 2 dx/dt =2t dy/dt = 15t2

Maksimum dan Minimum

Untuk fungsi perubah tiga z = f(x,y) maka titik stationer dapat merupakan ekstrem relatif, titik pelana dan titik belok, Dan syarat untuk mencapai titik ekstrem adalah:

1. Syarat perlu, adalah syarat orde pertama

dz/dx = fx = 0 dz/dy = fy = 0

2. Syarat cukup adalah syarat orde kedua Ekstem bila fxx fyy – fxy2 > 0

Titik pelana bila fxx fyy – fxy2 < 0

Ekstrem minimum bila fxx dan fyy > 0 Ekstrem maksimum bila fxx dan fyy < 0 tanda fxx dan fyy senantiasa sama

tanda fxx dan fyy senantiasa sama Contoh :

Z = -x2 _{+ 12x – y}2 _{+ 10y – 45}

Fx = dz/dx = -2x + 12 menjadi x = 6 Fy = dz/dy = -2y + 10 menjadi y = 5 Titik statisioner (6,5)

fxx = -2 fyy = -2 fxy = 0

fxx fyy – fxy2 = (-2) (-2) – 0 = 4 > 0 *titik ekstrem Fxx = -2 < 0 titik maksimum



Polinom atau suku banyak dalam X atau P(X) ialah

ungkapan yang mengandung suku KX

r

, dimana K

= konstanta serta r = bilangan bulat. Derajat

polinom adalah harga tertinggi r dalam P(X).

Fungsi polinom mempunyai bentuk umum:



Fungsi polinom mempunyai bentuk umum:

Y = a

₀

+ a1X + a

₂

X

2

+ ….. + a

_n

X

n



Fungsi polinom derajat dua atau fungsi kuadrat

 Bentuk umum : Y = aX2 + bX + c, dimana a,b dan c = konstanta

Y = variabel tidak bebas X = variabel bebas

 Dalam menggambarkan grafik parabola : Y = aX2 + bX + c, dapat

di perhatikan hal-hal berikut :

1. Parabola termuka ke arah Y positif (terbuka keatas) bila a positif 2. Parabola terbuka ke arah Y negatif (terbuka ke bawah)bila a

negatif negatif

3. Intersep = c

4. Harga x dan 2, yang cepat riil, berimpit atau hayal

a

ac

b

b

x

2

4

2 2

, 1





 Jika diskriminan (D) = b2 – 4ac > 0 maka terdapat 2 titik potong, yaitu :

jadi titik potong dengan sumbu Y = 0 adalah

dan

Jika D = b2 _{– 4ac = 0, maka hanya terdapat satu titik potong. Yaitu :}

a ac b a b x 2 4 2 2 1     a ac b a b x 2 4 2 2 2             _{ }

 ,0

2 4 2 a ac b b         _{ }

 ,0

2 4 2 a ac b b

 Jika D = b2 – 4ac = 0, maka hanya terdapat satu titik potong. Yaitu :

jadi titik potong dengan sumbu Y = 0 adalah :

 Jika D = b2 – 4ac < 0, maka tidak terdapat titik potong dengan sumbu X.

a b x x 2 2

1   

   



  ,0 2a

5. Sumbu parabola adalah

Disubstitusikan pada persamaan : Y = aX2 _{+ bX + c , maka}

a

b

x

x

x

2

2

2

1









ac

b

y

c

b

y

c

a

b

a

b

a

y

4

2

2

2 2 2 2

































Sehingga titik puncak parabola :

Contoh : gambarkan grafik fungsi : Y = x2 _{– 5X + 6 !!!}

 Fungsi Pangkat Banyak

jika Y = Xn_{atau Y = aX c,}

dimana: n = pangkat

n, x, a, c = bilangan real

 Fungsi Eksponen

Adalah suatu fungsi dimana variabel bebasnya merupakan pangkat dari suatu konstanta

Contoh : Y = f(X) = aX Contoh : Y = f(X) = aX

dimana; a = konstanta dan a>0 x dan Y = variabel

Karena a>0, maka nilai fungsinya selalu positif, sehingga diagram fungsinya terletak diatas sumbu X. Makin besar harga a maka diagram fungsi makin mendekati sumbu Y. Bilangan pokok yang sering dipakai adalah e =

2,7182818128……



Kaidah eksponensial yang penting :

n m n m q q l k

a

a

a

a

a

k

a

a











  / 0

1

1

Contoh : Gambarkan grafik fungsi Y = 2

X

!!!



Fungsi Logaritma adalah suatu fungsi non-linier

dimana variabel bebasnya dalam bentuk

logaritma.

Bentuk umum : Y =

a

log X

Dimana; a > 0 dan a

≠ 1

Dimana; a > 0 dan a

≠ 1



Fungsi log Y = f(X) =

a

log X merupakan invers

dari fungsi eksponen Y = g(X) = a

X

. Karena itu

diagram fungsi logaritma merupakan bayangan

pencerminan terhadap garis diagram dari fungsi

eksponen. Fungsi logaritma tidak memotong

sumbu Y.



Fungsi Hiperbolik

Fungsi pecah adalah fungsi non-linier yang

variabel bebasnya merupakan penyebut. Grafik

dari fungsi ini berbentuk Hiperbola.

Bentuk umum :

b

aX



Fungsi Hiperbolik

dimana; a,b,c dan d = konstanta

X = variabel bebas

Y = variabel tidak bebas

d

cX

b

aX

Y

 Ciri matematis dari fungsi pecah :

1. Titik potong dengan sumbu Y pada X = 0 yaitu b/d. Jadi P

(0,b/d).

2. Titik potong dengan sumbu X pada Y = 0 yaitu

sehingga aX + b = 0 x = -b/a Jadi Q (-b/a,0)

3. Asimtot datar (horizontal) bila x = ~ , maka







b X



a Y /   

b

aX

Y







d

cX

b

aX





b/~ = 0 dan d/~ = 0 maka Y = a/c

4. Asimtot tegak (vertikal) bila Y = ~ , adalah

, cX + d = 0 X = -d/c Jadi asimtot tegak adalah X = -d/c



d X



c Y /   d cX b aX Y   

d

cX

Y





d

cX

b

aX















[image:73.842.65.803.51.552.2]



Contoh : jika diketahui

Gambarkan grafik fungsinya !

1

3

2







 Fungsi linear sangat lazim diterapkan dalam ilmu ekonomi, baik dalam pembahasan ekonomi mikro maupun makro. Dua variabel ekonomi maupun lebih yang saling berhubungan acapkali diterjemahkan kedalam bentuk sebuah persamaan linear. Secara bertahap akan dibahas :

 Penerapan fungsi linear dalam teori ekonomi mikro.

1.Fungsi permintaan, fungsi penawaran dan keseimbangan pasar

Pengaruh pajak-spesifik terhadap keseimbangan pasar

2.Pengaruh pajak-spesifik terhadap keseimbangan pasar

3.Pengaruh pajak-proporsional terhadap keseimbangan pasar 4.Pengaruh subsidi terhadap keseimbangan pasar

5.Keseombangan pasar kasus dua macam barang 6.Fungsi biaya dan fungsi penerimaan

 Bentuk umum fungsi permintaan

bP

a

Q





a

P

Q

b

b

a

P

atau

1





Kurva Permintaan

b

a

Q

 Bentuk umum fungsi penawaran

P

a

atau

bP

a

Q

1











Kurva Penawaran

b

a

Q

0

a



Q

b

b

a

 Keseimbangan Pasar

Qd : jumlah permintaan Qs : jumlah penawaran E : titik keseimbangan

s

d

Q

Q



P

s

Q

E

P_e : harga keseimbangan Q_e : jumlah keseimbangan

e

P

Q

0

Q

_e

d

Q

Contoh Kasus 1 :

Diketahui : Fungsi Permintaan ; P = 15 – Q

Fungsi Penawaran ; P = 3 + 0,5 Q

Ditanyakan : P_e dan Q_e?...

Jawab : permintaan; P = 15 – Q Q = 15 – P keseimbangan penawaran; P = 3 + 0,5 Q Q = - 6 + 2P pasar; Q_d = Q_s

15 – P = - 6 + 2P

P

15 15 – P = - 6 + 2P

21 = 3P, P = 7

Q = 15 – P

= 15 – 7 = 8

Jadi, P_e= 7

Q_e = 8

7

Q

0

₈

d

Q

s

Q

E

15

15

 Pengaruh Pajak.

Pajak yang dikenakan atas penjualan suatu barang menyebabkan harga jual barang tersebut naik. Sebab setelah dikenakan pajak, produsen akan berusaha mengalihkan (sebagian) beban pajak tersebut kepada konsumen.

konsumen.

 Pengenaan pajak sebesar t atas setiap unit barang yang

 Contoh Kasus 2 :

Diketahui : permintaan; P = 15 – Q

penawaran; P = 3 + 0,5 Q

pajak; t = 3 per unit.

Ditanyakan : berapa P dan Q keseimbangan sebelum dan sesudah pajak ?...

Penyelesaian :

Dimisalkan sebelum pajak, P_e = 7 dan Q_e = 8 . Sesudah pajak, harga jual yang ditawarkan oleh produsen menjadi lebih tinggi, persamaan penawarannya berubah dan kurvanya bergeser keatas.

Penawaran sebelum pajak : P = 3 + 0,5 Q

Penawaran sesudah pajak : P = 3 + 0,5 Q + 3 = 6 + 0,5 Q Sedangkan permintaan tetap : P = 15 – Q

Keseimbangan Pasar : P_d = 15 – Q = 6 +0,5Q  -1,5Q = -9 Q = 6

Jadi, Kurvanya adalah sebagai berikut :

P

s

Q

15

9

s

Q

'

(sebelum pajak) (sesudah pajak)

'

E

7

Q

0

8

d

Q

E

15

6

3

9

 Beban pajak yang ditanggung konsumen (tk)

Rumus : tk = P’_e – P

Dalam contoh kasus diatas, tk = 9 – 7 = 2

 Beban pajak yang ditanggung produsen (tp)

Besarnya bagian dari beban pajak yang ditanggung oleh produsen (tp) adalah selisih antara besarnya pajak per unit barang (t) dan bagian pajak yang menjadi tanggungan konsumen barang (t) dan bagian pajak yang menjadi tanggungan konsumen

(tk).

Rumus : tp = t – tk

Dalam contoh kasus 2, tp = 3 – 2 = 1

 Jumlah pajak yang diterima oleh pemerintah (T)

Rumus : T = Q’_e X t

 Pajak Proporsional ialah pajak yang besarnya diterapkan berdasarkan persentase tertentu dari harga jual; bukan diterapkan secara spesifik (misalnya 3 rupiah) per unit barang. Meskipun pengaruhnya serupa dengan pengaruh pajak spesifik, menaikan harga keseimbangan dan mengurangi jumlah keseimbangan, namun analisisnya sedikit berbeda.

 Jika persamaan penawaran semula P = a + bQ (atau Q = -a/b + 1/b P) maka, dengan dikenakannya pajak proporsional sebesar t% dari harga jual, persamaan penawaran yang baru akan menjadi :

penawaran yang baru akan menjadi :

P = a + bQ + tP t : pajak proporsional dalam % P – tP = a + bQ

(l – t)P = a + bQ

   

 

b

P

t

l

b

a

Q

atau

Q

t

l

b

t

l

a

P













 Contoh Kasus 3 :

Diketahui : permintaan; P = 15 – Q

penawaran; P = 3 + 0,5 Q t = 25%

Ditanyakan : berapa P dan Q keseimbangan sebelum dan sesudah pajak ?...

Penyelesaian :

Sebelum pajak, Pe = 7 dan Qe = 8 , sesudah pajak, persamaan penawarannya akan berubah, sementara permintaannya tetap P = 15 – Q atau Q = 15 – P .

Penawaran sesudah pajak, dengan t = 25% = 0,25 : P = 3 + 0,5 Q + 0,25 P

P = 3 + 0,75 Q P = 3 + 0,75 Q

Keseimbangan Pasar : P_d= P_s

15 - Q = 3 +0,75Q -1,75Q = -12

Q = 6,6

Jadi, sesudah pajak : P’_e = 8,4 dan Q’_e = 6,6

Pajak yang diterima oleh pemerintah dari setiap unit barang adalah :

Kurvanya adalah :

P

7

s

Q

E

4 , 8

s

Q

'

'

E

 Besarnya pajak yang ditanggung oleh konsumen untuk setiap barang yang dibeli adalah tk = P’e – Pe = 8,4 – 7 = 1,4

 Sedangkan yang ditanggung produsen adalah : tp = t – tk = 2,1 – 1,4 = 0,7

 Jumlah pajak yang diterima oleh pemerintah adalah :

T = Q’e x t = 6,6 x 2,1 = 13,86.

Q

0

8

d

Q

 Subsidi merupakan kebalikan atau lawan dari pajak, oleh karena itu ia

sering juga disebut pajak negatif. Seiring dengan itu, pengaruhnya terhadap keseimbangan pasar berbalikan dengan pengaruh pajak, sehingga kita dapat menganalisisnya seperti ketika menganalisis pengaruh pajak. Subsidi dapat bersifat spesifik dan dapat juga bersifat proporsional.

proporsional.

 Pengaruh Subsidi. Subsidi yang diberikan atas produksi/penjualan

sesuatu barang menyebabkan harga jual barang tersebut menjadi lebih rendah. Dengan adanya subsidi, produsen merasa ongkos produksinya menjadi lebih kecil sehingga ia bersedia menjual lebih murah.

 Dengan subsidi sebesar s, kurva penawaran bergeser sejajar kebawah, dengan penggal yang lebih kecil (lebih rendah) pada sumbu harga.

 Contoh Kasus 4 :

Diketahui : permintaan; P = 15 – Q

penawaran; P = 3 + 0,5 Q

subsidi; s = 1,5 per unit.

Ditanyakan : berapa P dan Q keseimbangan sebelum dan sesudah subsidi ?...

Penyelesaian :

Tanpa subsid, Pe = 7 dan Qe = 8 . Dengan subsidi, harga jual yang ditawarkan oleh produsen menjadi lebih rendah, persamaan penawaran berubah dan kurvanya bergeser turun.

Penawaran tanpa subsidi : P = 3 + 0,5 Q

Penawaran dengan subsidi : P = 3 + 0,5 Q – 1,5

P = 1,5 + 0,5 Q  Q = -3 + 2P Permintaan tetap : P = 15 – Q  Q = 15 – P Maka, keseimbangan pasar : Q_d = Q_s

15 – P = -3 + 2P  18 = 3P, P = 6

 Jadi kurvanya sebagai berikut :

P

s

Q

E

15

s

Q

'

(dengan subsidi)

(tanpa subsidi)

6

Q

0

9

d

Q

15

3

5 , 1

7

E

'

 Bagian subsidi yang dinikmati konsumen. Besarnya bagian

dari subsidi yang diterima, secara tidak langsung, oleh konsumen (sk) adalah selisih antara harga keseimbangan tanpa subsidi (P_e ) dan harga keseimbangan dengan subsidi

(P’_e )



Dalam contoh kasus diatas,

sk =

7 – 6 = 1.

 Bagian subsidi yang dinikmati produsen.

sk

s

sp





e e

P

P

sk





'



Dalam contoh kasus diatas,

sp =

1,5 – 1 = 0,5.

 Jumlah subsidi yang dibayarkan oleh pemerintah.

Besarnya jumlah subsidi yang diberikan oleh pemerintah (S)

dapat dihitung dengan mengalikan jumlah barang yang terjual sesudah subsidi (Q’_e) dengan besarnya subsidi per unit barang (s).



Dalam contoh kasus diatas,

S =

9 x 1,5 = 13,5.

sk

s

sp





s

Q

 Bentuk Umum :

Qdx : jumlah permintaan akan X

Q_dy : jumlah permintaan akan Y

P_x : harga X per unit

P_y : harga Y per unit







_{y x}



dy

y x

dx

P

P

g

Q

P

P

f

Q

,

,





 _{Contoh Kasus 5 :}

Diketahui : permintaan akan X; Q_dx = 10 – 4P_x + 2P_y

penawarannya; Q_sx = -6 + 6P_x

permintaan akan Y; Q_dy= 9 – 3 P_y + 4 P_x

penawarannya; Q_sx= -3 + 7 P_y

Penyelesaian :

1) Keseimbangan pasar barang X

Q_dx = Q_sx

10 – 4P_x + 2P_y = -6 + 6P_x

10P_x – 2P_y = 16

2) Keseimbangan pasar barang Y

Qdy = Qsy

9 – 3P_y + 4P_x = -3 + 7 _Py

4P_x – 10 P_y = - 12

3) Dari 1) dan 2) : 3) Dari 1) dan 2) :

P_y = 2 , masukkan ke 1) atau 2), diperoleh P_x = 2

Masukkan kedalam persamaan semula, sehingga didapat nilai Q_xe = 6, dan nilai Q_ye = 11.

 Fungsi Biaya. Biaya total (total cost) yang dikeluarkan oleh sebuah

perusahaan dalam operasi bisnisnya terdiri atas biaya tetap (fixed cost)

dan biaya variabel (variable cost).

 

 

Q FC VC k vQ g

C

vQ Q

f VC

k FC

 

 



 



 

Q FC VC k vQ g

C     

FC : biaya tetap

VC : biaya variabel

C : biaya total

k : konstanta

v : lereng kurva VC dan kurva C

k

vQ VC 

0

k FC

Q

vQ

k

C





Contoh Kasus 6 :

Diketahui : FC = 20.000 , VC = 100 Q

Ditanyakan : Tunjukkan persamaan dan kurva totalnya !!! Berapa biaya total yang dikeluarkan jika diproduksi 500 unit barang ???

Penyelesaian :

C = FC + VC  C = 20.000 + 100 Q

Jika Q = 500, maka ; C = 20.000 + 100 (500) = 70.000

Q

C



20

.

000



100

C

000 .

20

Q VC  100

0

FC

Q

Q

C



20

.

000



100

C

000 .

50

000 .

70

 Fungsi Penerimaan. Penerimaan sebuah perusahaan dari

hasil penjualan barangnya merupakan fungsi dari jumlah barang yang terjual atau dihasilkan.

Semakain banyak barang yang diproduksi dan terjual, semakin besar pula penerimaannya. Penerimaan total

(total revenue) adalah hasilkali jumlah barang yang terjual

(total revenue) adalah hasilkali jumlah barang yang terjual dengan harga jual per unit barang tersebut. Secara matematik, penerimaan merupakan fungsi jumlah barang, kurvanya berupa garis lurus berlereng positif dan bermula dari titik pangkal.

 

Q

f

P

Q

Contoh Kasus 7 :

Harga jual produk yang dihasilkan oleh sebuah perusahaan Rp. 200,00 per unit. Tunjukkan persamaan dan kurva penerimaan total perusahaan ini !!!

Berapa besar penerimaannya bila terjual barang sebanyak 350 unit ???

Penyelesaian :

R = Q X P = Q X 200 = 200 Q

Bila Q = 350, maka ; R = 200 X 350 = 70.000

R

R



200

Q

Q

R

000

.

40

0

000

.

70

 Keuntungan (profit positif, π > 0) akan didapat apabila R > C .

 _Kerugian (profit negatif, π < 0) akan dialami apabila R < C .

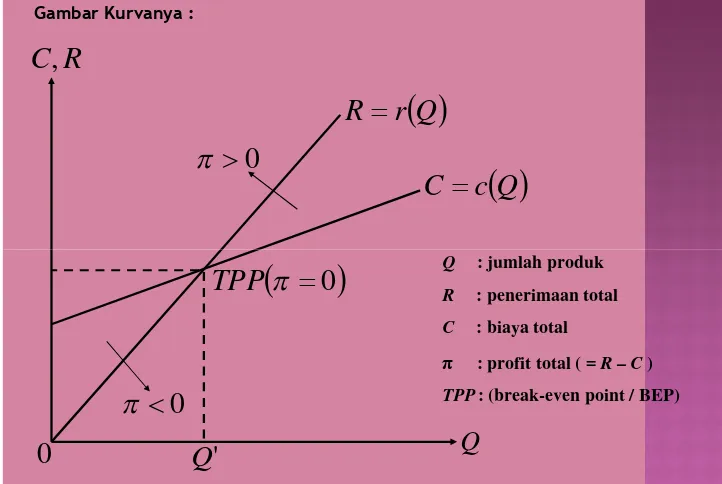
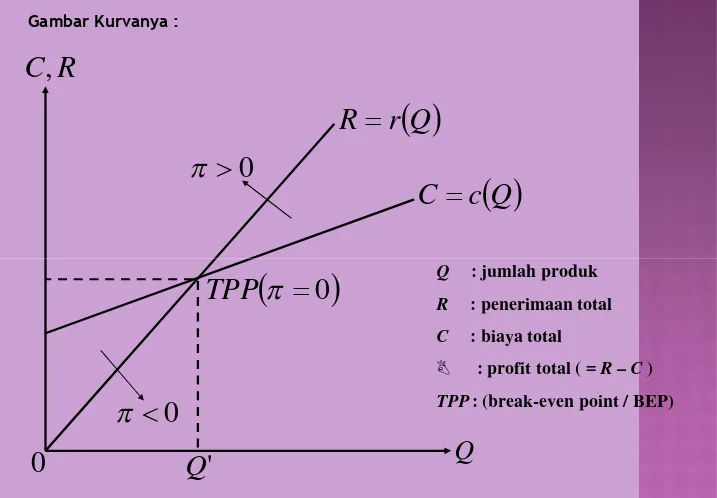
 Konsep yang lebih penting berkenaan dengan R dan C adalah konsep pulang-pokok (break-even), yaitu suatu konsep yang digunakan untuk pulang-pokok (break-even), yaitu suatu konsep yang digunakan untuk menganalisis jumlah minimum produk yang harus dihasilkan atau terjual agar perusahaan tidak mengalami kerugian. Keadaan break-even (profit nol, π = 0) terjadi apabila R = 0; perusahaan tidak memperoleh keuntungan tetapi tidak pula mengalami kerugian. Secara grafik, hal ini ditunjukkan oleh perpotongan antara kurva R dan kurva

[image:97.842.58.780.48.532.2]

Gambar Kurvanya :

R

C

,

 

Q

c

C



 

Q

r

R



0





Q







0



TPP

'

Q

0

0





Q : jumlah produk

R : penerimaan total

C : biaya total

π : profit total ( = R – C )

Contoh Kasus 8 :

Diketahui : C = 20.000 + 100 Q , R = 200 Q

Ditanyakan : Berapakah tingkat produksi pada saat BEP _{???.. Apa yang}

terjadi pada saat produksinya sebanyak 300 unit ???...

Penyelesaian :

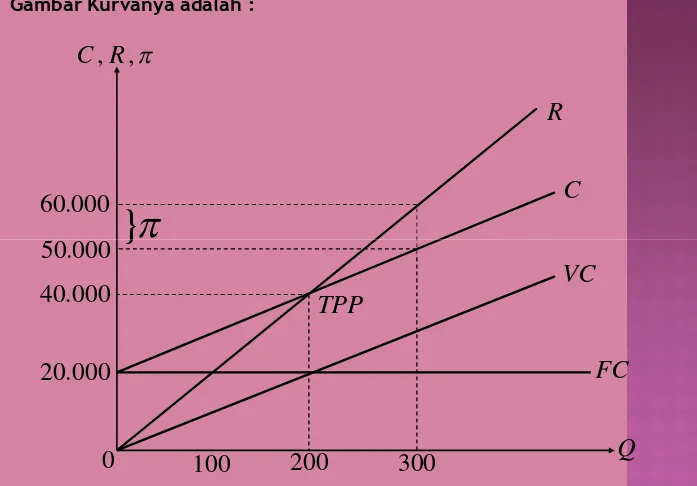
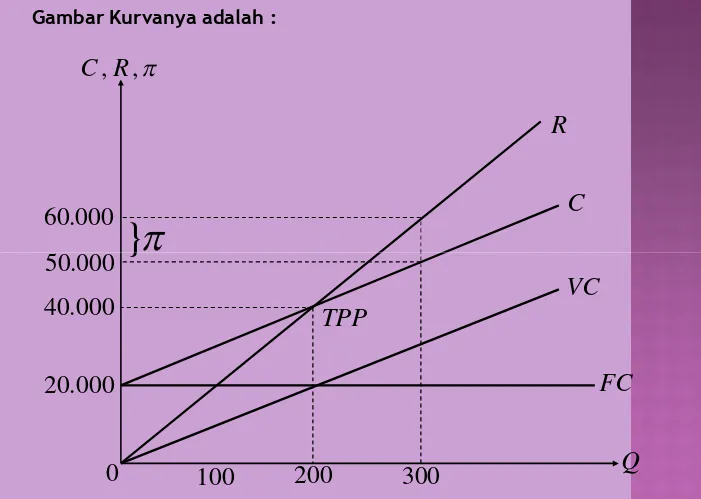
π = R – C jika Q = 300, maka : BEP ; π = 0,  R – C = 0 R = 200 (300) = 60.000 BEP ; π = 0,  R – C = 0 R = 200 (300) = 60.000

R = C C = 20.000 + 100 (300) 200 Q = 20.000 + 100 Q = 50.000

100 Q = 20.000

Q = 200 Keuntungan ; π = R – C

[image:99.842.76.773.58.544.2]

Gambar Kurvanya adalah :



,

,

R

C

C

R



}

000

.

60

Q

VC

FC

0

TPP



}

100

200

300

000

.

20

000

.

40

000

.



DEFINISI FUNGSI,

JENIS FUNGSI,



JENIS FUNGSI,

•Fungsi adalah suatu hubungan antara dua buah

variabel atau lebih, dimana masing-masing dari dua buah variabel atau lebih tersebut saling pengaruh-mempengaruhi.

•Sebuah Variabel adalah suatu jumlah yang mempunyai

nilai yang berubah-ubah pada suatu soal.

•Variabel yang terdapat dalam suatu fungsi dapat

dibedakan atas varibel bebas (independent variabel) dan variabel yang dipengaruhi/tidak bebas (dependent dan variabel yang dipengaruhi/tidak bebas (dependent variabel).

Contoh :

a) Y = f (X) atau Y = f (X1, X2)

X, X1, X2 = variabel bebas (independent variabel)

Y = variabel yang dipengaruhi (dependent Variabel) b) Y = a + bX

a dan b = Konstanta

 Fungsi Eksplisit : adalah suatu fungsi dimana antara variabel

bebas dan tidak bebas dengan jelas dibedakan. Contoh : Y = f (X) Y = 2X + 4

Fungsi diatas merupakan fungsi eksplisit dengan satu variabel bebas. Sedangkan

Y = 2X₁ + 3X₂ + 3 adalah fungsi eksplisit dengan dua variabel bebas

 Fungsi Implisit : adalah fungsi dimana antara variabel bebas dan  Fungsi Implisit : adalah fungsi dimana antara variabel bebas dan

variabel tidak bebas tidak dapat dengan mudah/jelas dibedakan. Bentuk umum dari fungsi implisit ini dinyatakan dengan :

f (X) = 0 untuk satu variabel f (X,Y) = 0 untuk dua variabel

f (X, Y, Z) = 0 untuk tiga variabel, dstnya contoh : 6X + 4Y – 7 = 0

Fungsi Linier/garis lurus adalah suatu fungsi

dimana variabel bebasnya paling tinggi

berpangkat satu.

Bentuk umum : Y = bX + a

a dan b = konstanta

a dan b = konstanta



Persamaan sebuah garis yang menelusuri/melewati

satu buah titik (X

₁

,Y

₁

) yaitu :

1

Y

Y

b

tg















₁ 1₁



1

1 1

bX

Y

bX

Y

X

X

b

Y

Y

X

X

b

tg



















 Persamaan sebuah garis yang menelusuri/melewati dua buah titik (X₁,Y₁) dan (X₂,Y₂) yaitu :

1 2

1

Y

Y

Y

Y

b

tg













 Dua garis linier dapat berimpit, sejajar, tegak lurus dan

berpotongan.

Dengan persamaan garis linier : g₁ : Y = bX + a

g₂ : Y’= b’X + c maka,

 Dua garis (g dan g ) akan sejajar bila tg kedua garis tersebut  Dua garis (g₁ dan g₂) akan sejajar bila tg kedua garis tersebut

sama atau b = b’

 Dua garis akan tegak lurus bila tg kedua garis pertama

dikalikan tg garis kedua sama dengan minus 1 atau b.b’ = -1

 Dua garis akan berimpit bila kedua persamaan garis tersebut

identik

1.

Gambarkan grafik fungsi: Y = 3X + 2

2.

Sebuah garis membentuk sudut 135

0

dengan

sumbu X positif dan melewati titik (3,4).

Ditanyakan persamaan garis serta

gambarkan grafik fungsinya dan apakah

gambarkan grafik fungsinya dan apakah

garis itu melewati titik P(2,3) dan titik

Q(2,5) ?

3.

Sebuah garis melewati titik A(2,1) dan

B(3,4). Ditanyakan persamaan garisnya!

4.

Hitung titik potong P dari dua persamaan

garis:

[image:108.842.63.743.88.523.2]

1. Fungsi permintaan, fungsi penawaran dan

keseimbangan pasar

2. Pengaruh pajak-spesifik terhadap

keseimbangan pasar

3. Pengaruh pajak-proporsional terhadap

keseimbangan pasar keseimbangan pasar

4. Pengaruh subsidi terhadap keseimbangan

pasar

5. Keseombangan pasar kasus dua macam

barang

6. Fungsi biaya dan fungsi penerimaan



Bentuk umum fungsi permintaan

bP

a

Q





a

P

Q

b

b

a

P

atau

1





Kurva Permintaan

b

a

Q

atau

bP

a

Q







P

Q

b

b

a

P

atau

1





Kurva Penawaran

b

a

Q

0

s

d

Q

Q



P

s

Q

e

P

Q

0

Q

_e

d

Q

Contoh Kasus 1 :

Diketahui : Fungsi Permintaan ; Q = 15 – P

Fungsi Penawaran ; Q = - 6 + 2P Ditanyakan : P_e dan Q_e ?...

Jawab : keseimbangan pasar; Q_d = Q_s

15 – P = - 6 + 2P

P

15 15 – P = - 6 + 2P

21 = 3P, P = 7

Q = 15 – P

= 15 – 7 = 8

Jadi, P_e= 7

Q_e = 8

7

Q

0

₈

d

Q

s

Q

E

15

15



Pengaruh Pajak.

Pajak yang dikenakan atas penjualan suatu

barang

menyebabkan

harga

jual

barang

tersebut

naik.

Sebab

setelah

dikenakan

pajak, produsen akan berusaha mengalihkan

(sebagian) beban

pajak tersebut

kepada

(sebagian) beban

pajak tersebut

kepada

konsumen.



Pengenaan pajak sebesar

t

atas setiap unit

barang

yang

dijual

menyebabkan

kurva

penawaran bergeser ke atas, dengan penggal

yang lebih tinggi pada sumbu harga. Jika

sebelum pajak persamaan penawarannya

P =

 Contoh Kasus 2 :

Diketahui : permintaan; P = 15 – Q

penawaran; P = 3 + 0,5 Q

pajak; t = 3 per unit.

Ditanyakan : berapa P dan Q keseimbangan sebelum dan sesudah pajak ?...

Penyelesaian :

Dimisalkan sebelum pajak, P_e = 7 dan Q_e = 8 . Sesudah pajak, harga jual yang ditawarkan oleh produsen menjadi lebih tinggi, persamaan penawarannya berubah dan kurvanya bergeser keatas.

penawarannya berubah dan kurvanya bergeser keatas.

Penawaran sebelum pajak : P = 3 + 0,5 Q

Penawaran sesudah pajak : P = 3 + 0,5 Q + 3 = 6 + 0,5 Q

Sedangkan permintaan tetap : P = 15 – Q

Keseimbangan Pasar : P_d = 15 – Q = 6 +0,5Q  -1,5Q = -9 Q = 6

Jadi, Kurvanya adalah sebagai berikut :

P

s

Q

15

9

s

Q

'

(sebelum pajak) (sesudah pajak)

'

E

7

Q

0

8

d

Q

E

15

6

3

9



Beban pajak yang ditanggung konsumen

(tk)

Rumus : tk = P’e – P

Dalam contoh kasus diatas, tk = 9 – 7 = 2



Beban pajak yang ditanggung produsen

(tp)

Besarnya bagian dari beban pajak yang ditanggung oleh produsen

(tp) adalah selisih antara besarnya pajak per unit barang (t) dan

(tp) adalah selisih antara besarnya pajak per unit barang (t) dan bagian pajak yang menjadi tanggungan konsumen (tk).

Rumus : tp = t – tk

Dalam contoh kasus 2, tp = 3 – 2 = 1



Jumlah pajak yang diterima oleh pemerintah

(T)

Rumus : T = Q’e X t

 Pajak Proporsional ialah pajak yang besarnya diterapkan berdasarkan persentase tertentu dari harga jual; bukan diterapkan secara spesifik (misalnya 3 rupiah) per unit barang. Meskipun pengaruhnya serupa dengan pengaruh pajak spesifik, menaikan harga keseimbangan dan mengurangi jumlah keseimbangan, namun analisisnya sedikit berbeda.

 Jika persamaan penawaran semula P = a + bQ (atau Q = -a/b + 1/b P)

maka, dengan dikenakannya pajak proporsional sebesar t% dari harga jual, persamaan penawaran yang baru akan menjadi :

harga jual, persamaan penawaran yang baru akan menjadi :

P = a + bQ + tP t : pajak proporsional dalam % P – tP = a + bQ

(l – t)P = a + bQ

   

 

b

P

t

l

b

a

Q

atau

Q

t

l

b

t

l

a

P













 Contoh Kasus 3 :

Diketahui : permintaan; P = 15 – Q

penawaran; P = 3 + 0,5 Q t = 25%

Ditanyakan : berapa P dan Q keseimbangan sebelum dan sesudah pajak ?...

Penyelesaian :

Sebelum pajak, Pe = 7 dan Qe = 8 , sesudah pajak, persamaan penawarannya akan berubah, sementara permintaannya tetap

P = 15 – Q atau Q = 15 – P .

Penawaran sesudah pajak, dengan t = 25% = 0,25 :

P = 3 + 0,5 Q + 0,25 P = 3 + 0,75 Q

Keseimbangan Pasar : P_d = P_s

15 - Q = 3 +0,75Q -1,75Q = -12

Q = 6,6

Jadi, sesudah pajak : P’_e = 8,4 dan Q’_e = 6,6

Pajak yang diterima oleh pemerintah dari setiap unit barang adalah :

Kurvanya adalah :

P

7

Q

s

Q

E

4 , 8

s

Q

'

'

E

 Besarnya pajak yang ditanggung oleh konsumen untuk setiap barang yang dibeli adalah tk = P’e – Pe = 8,4 – 7 = 1,4

 Sedangkan yang ditanggung produsen adalah : tp = t – tk = 2,1 – 1,4 = 0,7

 Jumlah pajak yang diterima oleh pemerintah adalah :

T = Q’e x t = 6,6 x 2,1 = 13,86.

Q

0

8

d

Q