DISUSUN OLEH:
NAMA : ANA SARI YANI
KELAS : III.B
MATA KULIAH : ALJABAR LINIER
KATA PENGANTAR
Assalamu’alaikum Wr. Wb.
Alhamdulillah, Puji syukur penulis panjatkan kepada Allah SWT. Karena berkat rahmat karuniaNya lah kami dapat menyelesaikan Artikel Ruang Vektor Umum ini.
Dalam menyelesaikan tugas ini kami mendapat banyak sekali bantuan dari berbagai pihak dan media, untuk bantuan tersebut kami megucapkan banyak terima kasih. Dan tidak lupa kami menyampaikan ucapan terima kasih kepada Ibu Nyayu Fahriza,F.S,Si, mpd yang telah banyak memberi bimbingan serta petunjuk kepada kami.
Kami telah berusaha semaksimal mungkin dalam penyelesaian makalah ini, Kami pun menyadari bahwa tugas ini masih jauh dari kesempurnaan, untuk itu kami mohon maaf apabila masih terdapat kesalahan kekurangan. dan kami mengharapkan saran dan kritik yang membangun untuk kesempurnaan makalah ini.
Semoga makalah yang kami buat ini dapat berguna bagi penulis maupun pembaca, dan dapat dimanfaatkan sebagaimana mestinya.
Wassalmu’alaikum Wr. Wb.
Palembang, Desenber 2012
BAB V
RUANG VEKTOR UMUM
5.
1. Ruang Vektor Real
Dalam bagian ini kita akan mengatakan sekumpulan aksioma yang jika dipenuhi oleh sekelompok himpunan, maka himpunan tersebut dapat dikatakan vektor.
Aksioma Ruang Vektor. Definisi berikut terdiri dari sepuluh aksioma. Definisi :
Misalkan V adalah sembarang himpunan dengan elemen yang didalamnya diberikan operasi penjumlahan dan perkalian dengan skalar. Jika sepuluh aksioma ini dipenuhi oleh , , di V dan skalar k,l yang sembarang, maka kita dapat
Perhatikan ruang vektor R2 dan R3 yang telah dibahas pada bagian lain. Komponen-komponen yang terlibat dalam ruang vektor tersebut ialah:
1. Himpunan pasangan berurutan (2 bilangan real untuk R2 dan 3 bilangan real untuk R3)
2. Himpunan skalar (untuk mendefinisikan perkalian vektor dan skalar) 3. Operasi vektor (yaitu operasi tambah) yang memenuhi sifat-sifat tertentu 4. Operasi perkalian vektor dengan skalar yang memenuhi sifat-sifat tertentu
Contoh : Himpunan yang bukan merupakan Ruang Vektor.
Misalkan V = R2 dan didefinisikan operasi-operasi penjumlahan dan perkalian skalar sebagai berikut:
Jika u = (u1, u2) dan v = (v1, v2) maka didefinisikan u + v = ( u1 + v1 , u2 + v2 ) dan jika k adalah bilangan real sebarang, maka definisikan
ku = ( ku1 , 0 )
Sebagai contoh, jika u = (2,4), v = (-3,5), dan k = 7, maka u + v = ( 2 + (-3), 4 +5) = (-1, 9)
ku = 7u = ( 7 .2 , 0 ) = (14, 0)
Operasi penjumlahan merupakan operasi penjumlahan standar pada R2, tetapi operasi perkalian skalar bukan merupakan perkalian skalar standar. Pada bagian latihan, kami akan meminta anda untuk menunjukkan bahwa kesembilan aksioma ruang vektor pertama terpenuhi; namun demikian, terdapat nilai-nilai u yang menyebabkan Aksioma 10 tidak berlaku, sebagai contoh , jika u = (u1, u2) sedemikian rupa sehingga u2 0, maka
lu = l (u1, u2) = ( l . u1 , 0 ) = (u1 , 0) u
jadi, V bukan merupakan ruang vektor untuk operasi-operasi tersebut. Contoh : Ruang Vektor Nol
Misalkan V terdiri dari suatu objek tunggal, yang dinotasikan dengan 0, dan didefinisikan
Untuk semua skalar k. Pemeriksaan untuk mengetahui apakah semua aksioma ruang vektor telah terpenuhi dapat dilakukan dengan mudah. Kita menyebut ruang vektor ini sebagai ruang vektor nol.
Kita pelajari dari R2 dan R3 sifat-sifat berikut ini.
Jika A, B, C vektor di R2 atau R3 maka (A + B) + C = A + (B + C)
Ada suatu vektor yang disebut Vektor nol dan dilambangkan dengan O, yaitu (0,0) untuk R2 dan (0,0,0) untuk R3
Untuk setiap vektor A di R2 atau R3 ada vektor –A sehingga A + (-A) = O Untuk A dan B vektor di R2 atau R3 berlaku A + B = B + A
Untuk setiap skalar c dan vektor A dan B di R2 atau R3 berlaku c(A+B)=cA + cB Untuk skalar c1 dan c2 dan vektor A di R
2
atau R3 berlaku (c1+c2)A = c1A + c2A Untuk skalar c1 dan c2 dan vektor A, B di R2 atau R3 berlaku (c1c2)A = c1(c2A) Untuk skalar satuan 1 berlaku 1A = A untuk setiap A vektor di R2 ata R3
Sifat- sifat vektor
Kita akan membuktikan bagian (a) dan (c) dan meninggalkan bukti-bukti bagian yang lainnya sebagai latihan.
Bukti (a). kita dapat menulis 0u + 0u = ( 0 + 0 ) u [ aksioma 8 ]
= 0u [ sifat dari bilangan 0 ]
Teorema
Misalkan V adalah suatu ruang vektor, u adalah suatu vektor pada V, dan k adalah suatu skalar, maka:
a. 0u = 0
b. k0 = 0
c. (-1)u = -u
Berdasarkan aksioma 5, vektor 0u memiliki bentuknegative, -0u. dengan menambahkan negatifnya ini pada kedua ruas diatas dan menghasilkan
[0u + 0u ] + (- 0u ) = 0u + ( -0u )
Atau
0u + [0u + (-0u ) ] = 0u + ( -0u ) [ aksioma 3] 0u +0 = 0 [ aksioma 5 ] 0u = 0 [ aksioma 4 ]
Bukti (c). untuk menunjukkan (-1)u = -u, kami harus memperlihatkan bahwa u + (-1)u =0. Untuk melihat ini amati bahwa
u + (-1)u = Iu + (-1)u [ aksioma 10 ]
= (1 + (-1)) u [ aksioma 8 ] = 0u [ sifat dari bilangan ]
= 0 [ bagian (a) diatas ]
5.2
SubRuang ( Ruang Bagian)
Definisi:
Suatu sub himpunan W dari suatu ruang vektor V disebut subruang dari V jika W itu juga merupakan sebuah ruang vektor dibawah penjumlahan dan perkalian skalar yang didefinisikan pada V.
Jika W adalah himpunan dari satu atau lebih vektor dari sebuah ruang vektor V, maka W adalah subruang dari V jika dan hanya jika kondisi-kondisi berikut berlaku
1) Jika u dan v adalah vektor-vektor pada W, maka u + v terletak di W
Kondisi-kondisi (1) dan (2) sering kita jelaskan dengan menyatakan bahwa W tertutup dibawah penambahan dan tertutup di bawah perkalian skalar.
Bukti : jika W adalah subruang dari V, maka semua aksioma ruang vektor dipenuhi; khususnya Aksioma 1 dan Aksioma 6 berlaku. Tetapi dalam hal ini persis merupakan kondisi (1) dan kondisi (2).
Setiap ruang vektor pada V mempunyai paling sedikit dua subruang. V sendiri adalah sebuah subruang, dan himpunan {0} yang terdiri dari vektor nol saja pada V yang merupakan sebuah subruang yang kita namakan subruang nol (zero subspace).
Contoh:
Misalkan W sebarang bidang yang melalui titik asal dan misalkan u serta V sebarang vektor pada W. maka u + v harus terletak pada W karena u + v adalah diagonal jajaran genjang yang ditentukan oleh u dan v (gambar 1) dan k u harus terletak pada W untuk sebarang skalar k karena ku terletak pada garis yang melalui u. jadi W adalah subruang dari R3.
Contoh
Perlihatkan bahwa himpunan W dari semua matriks 2 x 2 yang mempunyai bilangan nol pada diagonal utamanya adalah subruang dari ruang vektor M22 dari semua matriks 2 x 2 Pemecahan.
Adalah seberang dua matriks pada W dan K adalah sebarang skalar. Maka
Oleh karena kA dan A + B mempunyai bilangan nol pada diagonal utama, maka kA dan A + B terletak pada W. Jadi, W adalah subruang dari M22.
Contoh:
Vektor-vektor i = (1, 0, 0) j = (0, 1, 0) dan k = (0, 0, 1) merentang R3 karena setiap vektor (a, b, c) pada R3 dapat kita tuliskan sebagai :
(a, b, c) = ai + bj + ck
Teorema : jika Ax = 0 adalah suatu sistem linier homogen yang terdiri dari m persamaan dengan n factor yang tidak diketahui, maka himpunan vektor solusinya adalah suatu subruang dari Rn.
Contoh: ruang solusi yang merupakan subruang R3
Perhatikan sistem-sistem linier berikut:
a) =
Penyelesaian:
Solusinya adalah x = 2s – 3t , y = s , z = t
Dimana selanjutnya x = 2y – 3z , atau x – 2y + 3z =0
Ini merupakan persamaan bidang yang melewati titik asal dengan n = (1, -2, 3) sebagai vektor normal.
Definisi:
Suatu vektor w disebut suatu kombinasi linier dari vektor – vektor v1, v2, …….vr jika dapat dinyatakan dalam bentuk w = k1v1 + k2 v2 …. + kr.vr
Dimana k1, k2,…..,, kr adalah skalar.
Teorema Merentang (spanning) : Jika v1, v2, ……….vr adalah vektor–vektor pada ruang vektor V, maka:
2) W adalah subruang terkecil dari V yang mengandung v1, v2, …….vr, adalah arti bahwa setiap subruang lain dari V yang mengandung v1, v2,…….,vr harus mengandung W
Kombinasi linear vi, v2, ……..vr, maka kita dapatkan subruang V. subruang tersebut kita namakan ruang linear terentang oleh {v1, v2, …….vr}, atau dengan lebih sederhana kita namakan ruang terentang oleh {v1, v2,…….vr}
Bukti :
a. Untuk memperlihatkan bahwa W adalah subruang V, kita harus membuktikan bahwa W tertutup dibawah penambahan dan perkalian skalar. Jika u dan v adalah vektor-vektor pada W, maka
u = c1v1 + c2v2 + ……… + crvr
dimana c1, c2, …….cr, k1, k2,…………kr adalah skalar. Maka,
u + v = (c1k1)v1 + (c2 + k2)v2 + ……… + (cr+kr)vr dan, untuk sebarang skalar k,
ku = (kc1) v1 + (kc2) v2 + ………..+ (kcr) vr
jadi u + v dan ku adalah kombinasi-kombinasi linear v1, v2, ……… vr, dan sebagai konsekuensinya maka u + v dan ku terletak di W sehingga W tertutup di bawah penambahan dan perkalian skalar.
b. Setiap vektor vi adalah kombinasi-kombinasi v1, v2, ……..vr, karenanya dapat kita tulis
vi = 0v1+0v2 + ………..+ 1vi + …………..0vr
oleh karena itu, subruang w mengandung setiap vektor v1, v2, …….vr misalkan W1 adalah sebarang subruang lain yang mengandung v1, v2, …….vr. karena W-1 tertutup di bawah penambahan dan perkalian skalar, maka W-1 harus mengundang semua kombinasi linear.
c1v1 + c2v2 dari v1,v2……,vr
Diketahui vektor-vektor = ( 1, 1, 0, 1) , = (2, 1, 1,1 ), dan = (1, 1, 1, -1 ) dalam R4. Tunjukkan bahwa vektor = (4, 3, 2, 1 ) merupakan kombinasi linier dari , , dan .
Penyelesaian:
Supaya menjadi kombinasi linier dari , , dan , maka harus ada skalar k1, , k2, k3 sehingga:
= k1 , k2 , k3 , atau dengan kata lain
(4, 3, 2, 1 ) = k1 ( 1, 1, 0, 1) + k2 (2, 1, 1,1 ) + k3 (1, 1, 1, -1 ) Didapat tiga persamaan, yaitu:;
4 = k1 + 2 k2 + k3 3 = k1 + k2 + k3 2 = k2 + k3 1 = k1 + k2 - k3
Untuk k1 = k2 = k3 = 1, maka = 1 + , ini artinya dapat disajikan sebagai kombinasi linier dari , , dan .
5.3 Kebebasan Linear
Ketahui bahwa ruang vektor V direntang oleh himpunan vektor S = [v1, v2……..vr] jika setiap vektor pada V adalah kombinasi linear, v1, v2……..vr. dengan merentang himpunan tersebut akan berguna dalam berbagai soal, karena mungkin kita sering menelaah ruang vektor V dengan menelaah terlebih dahulu vektor-vektor dengan merentang himpunan S. dan kemudian dengan memperluas hasil-hasil tersebut pada bagian selebihnya dari V. maka, kita perlu mempertahankan perentangan himpunan S sekecil mungkin. Permasalahan untuk mendapatkan peretangan himpunan terkecil untuk ruang vektor bergantung pada pengertian kita mengenai kebebasan linear.
Definisi. Jika S = {v1, v2……..vr} adalah himpunan vektor, maka persamaan vektor.
k1v1 + k2v2 + …………..krvr = 0
Mempunyai paling sedikit satu pemecahan, yakni
Jika ini adalah satu-satunya pemecahan, maka S kita namakan himpunan bebas linier (linearly independen). Jika ada pemecahan lain, maka S kita namakan himpunan
tak-bebas linier (linier dependent).
Contoh :
Himpunan vector-vektor , dimana v1= (2, -1, 0, 3), v2 = (1, 2, 5, -1), dan v3 = (7, -1, 5, 8) adalah himpunan tak bebas linier, karena 3v1 + v2 – v3 = 0.
Contoh :
Tinjaulah vektor-vektor i = (1, 0, 0), j = (0, 1, 0) dan k = (0, 0, 1) pada R3. Ruas komponen persamaan vector
K1 i + k2 j + k3 k = 0
K1(1, 0, 0) + k2(0, 1, 0) + k3(0, 0, 1) = 0
Jadi , K1 = 0, k2 = 0 dan k3 = 0; sehingga himpunan S = (i, j, k) bebas linier. Uraian serupa dapat digunakan untuk memperlihatkan bahwa vector-vector e1 = (0, 0, 0, … , 1), e2 = (0, 1, 0, 0, …, 0), … ,en = (0, 0, 0, …,0) membentuk himpunan bebas linier pada Rn.
Contoh
Tinjaulah vektor-vektor i = (1, 0, 0), j = (0, 1, 0), dan k = (0, 0, 1) pada R3 ruas komponen persamaan vektor
Kii + 1 + k2v2 + ………..krvr = 0 Menjadi
k1 = (1, 0, 0), + k2 (0, 1, 0) + k3(0, 0, 1) = (0, 0, 0) atau secara ekivalen menjadi
(k1, k2, k3) = (0, 0, 0)
Jadi, k1 = 0, k2 = 0, k3 =0; sehingga himpunan S = (i, j, k) bebas linear. Uraian serupa dapat digunakan untuk memperlihatkan bahwa vektor-vektor e1 = (1, 0, 0,……..0), e2= (0, 1, 0, …..0),…….,cn = (0, 0, 0,……..1) membentuk himpunan bebas linear pada Rn.
a) Tak bebas linear jika dan hanya paling tidak satu diantara vektor S dapat dinyatakan sebagai kombinasi linear dari vektor S lainnya
b) Bebas linear jika dan hanya jika tidak ada vektor S yang dapat dinyatakan sebagai kombinasi dalam linear dalam vektor S lainnya .
Teorema:
a) Jika sebuah himpunan mengandung vektor nol, maka himpunan itu takbebas linear
b) Sebuah himpunan yang mempunyai persis dua vektor tak bebas jika bebas satu dari vektor itu adalah perkalian dari skalar lainnya.
Contoh:
Dalam R2 atau R3 satu vektor adalah kelipatan skalar dari vektor lainnya jika hanya jika kedua vektor yang terletak pada garis yang sama yang melalui titik asal ditempatkan pada titik awalnya melalui titik asal. Jadi, berikutnya dari bagian (b) dari teorema 7 bahwa dalam R2 dan R3 dua vektor yang berbentuk himpunan tak bebas linear adalah jika dan hanya jika vektor itu terletak pada garis yang sama melalui titik asal yang ditempatkan pada titik awalnya melalui titik asal itu sendiri.
Teorema 8. misalkan S = {v1, v2, ……….vr) adalah himpunan vektor-vektor pada R n
jika r > n, maka S tak bebas linear.
Bukti.
v1 = (v11, v12, ……….v1n) v2 = (v21, v22, ……….v2n) vr = (vr1, vr2, ……….vrn) tinjaulah persamaan
kiv1 + k2v2 + ………..krvr = 0
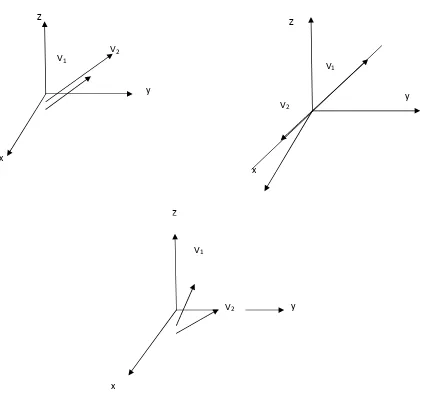
Interfretasi Geometris
• diR3, himpunan yang terdiri dari 3 vektor dikatakan bebas linear jika dan hanya jika vektor-vektor tersebut tidak berada pada bidang yang sama bila titik awal ketiga vektor tersebut berada pada origin
Contoh interpretasi geometric dari ketakbebasan linier dalam R2
Gambar 4.6 (a) takbebas linier, (b) takbebas linier, (C) bebas linier
5.4 Basis dan Dimensi
Definisi. Jika V adalah sebarang ruang vektor dan S = {V1, V2,...Vr} merupakan himpunan berhingga dari vektor-vektor pada V, maka S kita namakan basis untuk V jika
i. S bebes linear; ii. S merentang V
V2
V1
y
x x
y
Z Z
V2
V1
Z
V1
V2 y
Contoh:
Untuk melihat bahwa S bebas linear, anggaplah bahwa
aM1 + bM2 + cM3 + dM4 = 0
walaupun ruang vektor tersebut tidak mempunyai himpunan bebas linearm sehingga basispun tidak ada.
Teorema 9. Jika S = {V1,V2,….Vn} adalah basis untuk ruang vektor V, maka setiap himpunan dengan lebih dari n vektor adalah tak terbebas linear
Bukti
. Misalkan S= {W1, W2,….Wm} adalah sebarang himpunan m vektor pada V, dimana m>n. Kita ingin memperlihatkan bahwa S tak bebas linear. Karena S = {V1,V2….Vn} adalah sebuah basis maka setiap w dapat dinyatakan sebagai kombinasi linear dari vektor-vektor S, katakanlah,
w1 = a11v1 + a21v2 +………an1vn w1 = a12v1 + a22v2 +………an1vn
wm = a1mv1 + a2mv2 +………anmvn
Untuk memperlihatkan bahwa S tak bebas linear, maka kita harus cari skalar-skalar K1,K2…Km, yang tidak semuanya nol, sehingga
k1w1 + k2v2 +….………kmwm = 0
Teorema 10. Sebarang dua basis untuk ruang vektor berdimensi berhingga mempunyai jumlah vektor yang sama.
Bukti. :Misalkan S = {V1,V2….Vn} dan S {W1, W2,….Wm} adalah dua basis untuk sebuah ruang vektor V yang berdimensi berhingga. Karena S adalah sebuah basis dan S adalah himpunan basis linear, maka teorema 9 menunjukkan bahwa m≤n. Demikian juga, karena S adalah sebuah basis dan S bebas linear, kita juga memperoleh n≤m. maka m=n.
Definisi. Dimensi sebuah ruangan vektor V yang berdimensi berhingga didefinisikan sebagai banyaknya vektor pada basis untuk V. Tambahan lagi, kita mendefinisikan ruang vektor nol mempunyai dimensi nol.
Contoh
2x1 + 2x2 - x3 + x5 = 0
Sehingga vektor-vektor pemecahan tersebut dapat dituliskan sebagai
1 sebuah ruang V yang berdimensi n, maka S adalah sebuah basis untuk V.
b) Jika S = {V1,V2….Vn} adalah sebuah himpunan n vektor yang merentang ruang V yang berdimensi n, maka S adalah basis untuk V
DAFTAR PUSTAKA
Rorres, Anton. 2004. Aljabar Liniar Elementer versi aplikasi edisi kedelapan, jilid 1, Erlangga, Jakarta
Heri Purwanto, Gina Indriani, Erlina Dayanti. 2005. Aljabar Linier. PT Ercontara Rajawali; Jakarta