BAB 4 PROGRAM LINIER A. Pengertian Program Linier - Modul Siap UN Matematika SMA Program MIPA

(1)

5 3,5 7

x + y = 5 2x+y = 7

5 (2 , 3)

x y

a b

bx + ay = ab x + y = p

p

BAB 4

PROGRAM LINIER

A. Pengertian Program Linier

Program linier adalah suatu cara yang dapat digunakan untuk memecahkan permasalahan yang berhubungan dengan optimasi linier (nilai maksimum atau nilai minimum).

B. Grafik Himpunan Penyelesaian Pertidaksamaan Linier Dua Variabel

Contoh:

Gambarlah grafik x3y3, x0, dan y0 ! Jawab:

3 3 

 y

x

x y ( x , y )

0 1 ( 0 , 1 )

3 0 ( 3 , 0 )

Titik uji (0,0): x3y  3 0 + 3 (0)  3 0  3 Benar

Sehingga titik (0,0) termasuk daerah penyelesaian.

Jadi, daerah penyelesaiannya adalah sebelah bawah garis x3y3

Contoh:

1. Nilai minimal dari f(x,y)4x5y yang memenuhi pertidaksamaan 2x y7, x y5, x0, dan y0 adalah ....

Pembahasan:

Menentukan titik potong: 7

2xy xy5 x  2

Sehingga:

5  y x

5 )

2 ( y

2 5  y

3 

y , titik potongnya (2 , 3)

Titik Pojok Fungsi objektif

x y

3 1

(2)

90

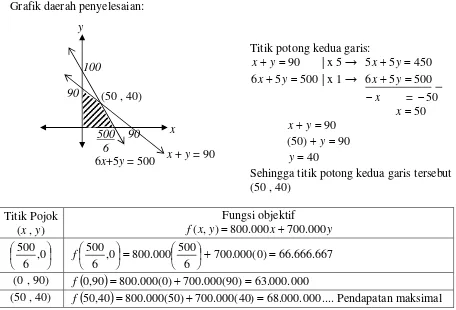
2. Sebuah pesawat dengan rute Jakarta – Surabaya dalam satu kali pemberangkatan dapat mengangkut penumpang paling banyak 90 penumpang yang terdiri dari penumpang kelas bisnis dan kelas ekonomi. Penumpang kelas bisnis boleh membawa barang seberat 12 kg dan kelas ekonomi 10 kg dengan daya angkut maksimal bagasi adalah 1.000 kg. Harga tiket penumpang kelas bisnis Rp800.000,00 dan kelas ekonomi Rp700.000,00. Pendapatan maksimal maskapai tersebut adalah .... Pembahasan:

Jika: banyak penumpang kelas bisnis = x banyak penumpang kelas ekonomi = y

maka, model matematikanya:

tentang banyak penumpang : x y90... (1) jumlah penumpang paling banyak 90 orang tentang daya angkut bagasi : 12x10y1.000... (2) maksimal bagasi menampung 1.000 kg

disederhanakan menjadi 6x5y500 syarat mutlak: x0 dan y0

Grafik daerah penyelesaian:

Titik potong kedua garis: 90

Sehingga titik potong kedua garis tersebut (50 , 40) Rp80.000,00 setiap pasang. Jika pedagang tersebut mempunyai modal sebesar Rp3.000.000,00 untuk membeli sepatu jenis I dan jenis II, maka model matematika dari permasalahan di atas adalah …. Pembahasan:

Jika: banyak sepatu jenis I = x banyak sepatu jenis II = y

maka, model matematikanya:

tentang daya tampung : x y40... (1) hanya cukup 40 berarti 

tentang modal : 60.000x80.000y3.000.000... (2) uang modal berarti  disederhanakan menjadi 3x4y150

(3)

x y

3 6

3 I II

III _IV

V

5 _{3x + 5y =15} 6x + 3y =18

2x + y =6

x y

2 3

2 4

2x + 4y = 8 x + 2y = 4 3x + 2y = 6

2. Daerah penyelesaian dari sistem pertidaksamaan linier       



 

  

0 0

6 2

15 5 3

y x

ditunjukkan pada gambar di

bawah ini dengan nomor daerah ….

Pembahasan:

Untuk menentukan  atau , kita lihat dari posisi daerah penyelesaiannya. Jika daerah penyelesaiannya di sebelah kiri atau bawah, maka . Sedangkan jika daerah penyelesaiannya di sebelah kanan atau atas, maka . Berarti daerah yang memenuhi:

15 5

3x y , 2x y6, x0, dan y0 adalah daerah I

3. Sistem pertidaksamaan linier yang memenuhi daerah yang diarsir pada gambar di bawah ini adalah ….

Pembahasan:

Karena daerah penyelesaiannya di bawah berarti sama-sama . Jadi sistem pertidaksamaan atau model matematika yang benar adalah x2y4, 3x2y6, x0, y0 (E)

4. Daerah yang diarsir pada gambar di bawah ini merupakan daerah penyelesaian suatu sistem pertidaksamaan linier. Nilai maksimal dari fungsi objektif f(x,y)5x6y adalah ....

x y

3 6

3 I II

III _IV

V

5

x y

2 3

2 4

(4)

x

5. Seorang penjahit membuat dua jenis pakaian untuk dijual. Pakaian jenis I memerlukan 2 m kain katun dan 4 m kain sutera, sedangkan pakaian jenis II memerlukan 5 m kain katun dan 3 m kain sutera. Bahan kain katun dan kain sutera yang tersedia masing-masing adalah 70 m dan 84 m. Pakaian jenis I dijual dengan laba Rp25.000,00 per pakaian, sedangkan pakaian jenis II Rp50.000,00 per pakaian. Agar ia memperoleh laba sebesar-besarnya, maka banyaknya pakaian jenis I dan jenis II masing-masing dibuat sebanyak ....

Pembahasan:

Jika: banyak pakaian jenis I = x banyak pakaian jenis II = y maka, model matematikanya:

Pakaian

Sehingga diperoleh sistem pertidaksamaan/model matematika: Kain katun: 2x5y70 .... (1)

Kain sutera: 4x3y84 .... (2)

Banyak pakaian jenis I dan II tidak mungkin negatif, berarti: 0 Grafik daerah penyelesaian:

(5)

x y

10 3

2 9 I

II III

IV V

15  x

Sehingga titik potong kedua garis tersebut (15 , 8)

Titik Pojok (x , y)

Fungsi objektif y x

y x

f( , )25.000 50.000 (21 , 0) f(21,0)25.000(21)50.000(0)525.000

(15 , 8) f(15,8)25.000(15)50.000(8)375.000400.000775.000 (0 , 14) f(0,14)25.000(0)50.000(14)700.000

Laba terbesar Rp775.000,00 dengan membuat 15 pakaian jenis I dan 8 pakaian jenis II.

LATIHAN UN:

1. Untuk membuat barang A diperlukan 6 jam pada mesin I dan 4 jam pada mesin II. Sedangkan membuat barang B diperlukan 2 jam pada mesin I dan 8 jam pada mesin II. Kedua mesin tersebut setiap harinya masing-masing bekerja tidak lebih dari 18 jam. Jika setiap hari membuat x barang A dan y barang B, maka model matematika permasalahan tersebut adalah ....

A. 2x3y9 ;4xy9 ;x0 ;y0 B. 3x2y9 ;2x4y9 ;x0 ;y0 C. 3xy9 ;2x4y9 ;x0 ;y0 D. x3y9 ;4x2y9 ;x0 ;y0 E. 4x3y9 ;x2y9 ;x0 ;y0

2. Daerah yang memenuhi sistem pertidaksaman linier 3xy9; x5y10; x0; y0; x,yR adalah ....

A. I B. II C. III D. IV E. V

3. Sistem pertidaksamaan linier yang memenuhi daerah penyelesaian (daerah yang diarsir) pada grafik di bawah ini adalah ….

A. 5x6y30, xy1, x4, y0 B. 5x6y30, xy1, x4, y0 C. 5x6y30, xy1, x4, y0

x y

1

–1 4 6

(6)

4. Diketahui sistem pertidaksamaan 2x3y24, xy10, x10, dan y0. Nilai maksimum dari fungsi objektif f(x,y)2.000x1.000y adalah ….

A. 8.000 B. 10.000 C. 16.000 D. 20.000 E. 24.000

5. Pada grafik di bawah ini, daerah yang diarsir merupakan himpunan penyelesaiaan program linier.

Nilai maksimum dari fungsi objektif f(x,y)2x5y pada grafik di atas adalah …. A. 15

B. 20 C. 25 D. 26 E. 30

6. Pada grafik di bawah ini, daerah yang diarsir adalah penyelesaiaan dari program linier. Nilai maksimum f(x,y)8x2y adalah ….

A. 4 B. 8 C. 9 D. 14 E. 16

7. Seorang pedagang kue akan menjual dua jenis kue. Harga beli setiap kue A Rp3.000,00, lalu dijual dengan keuntungan Rp1.000,00 per kue. Harga beli setiap kue B Rp4.000,00, lalu dijual dengan keuntungan Rp1.500,00 per kue. Modal yang dimiliki adalah Rp1.700.000,00. Setiap hari paling banyak dapat menjual 500 kue. Jika kue tersebut terjual habis, maka keuntungan maksimum yang diperoleh pedagang tersebut adalah ....

A. Rp500.000,00 B. Rp537.500,00 C. Rp600.000,00 D. Rp637.500,00 E. Rp750.000,00

x y

2

2 3 4

y = 2 1 1

x y

5

15 10

(7)

8. Tempat parkir seluas 600 m hanya mampu menampung bus dan mobil sebanyak 58 buah. Tiap 2 mobil memerlukan tempat 6 m dan bus 24 2 _{m . Biaya parkir tiap mobil Rp5.000,00 dan bus}2 Rp7.500,00. Jika tempat parkir penuh, maka hasil dari biaya parkir paling banyak adalah ....

A. Rp197.500,00 B. Rp220.000,00 C. Rp290.000,00

D. Rp325.000,00 kunci E. Rp500.000,00

9. Menjelang hari raya Idul Adha, Pak Mahmud hendak berjualan sapi dan kerbau. Harga seekor sapi dan kerbau di Jawa Tengah berturut-turut Rp9.000.000,00 dan Rp8.000.000,00. Modal yang beliau miliki Rp124.000.000,00. Pak Ahmad menjual sapi dan kerbau di Jakarta dengan harga Rp10.300.000,00 dan Rp9.200.000,00. Kandang yang beliau miliki hanya dapat menampung tidak lebih dari 15 ekor. Agar diperoleh keuntungan maksimum, maka banyak sapi dan kerbau yang harus dibeli Pak Mahmud adalah .... ekor.

A. 11 dan 4

B. 4 dan 11 kunci C. 13 dan 2

D. 0 dan 15 E. 7 dan 8

10. Suatu perusahan meubel memerlukan 18 unsur A dan 24 unsur B per hari. Untuk membuat barang jenis I dibutuhkan 1 unsur A dan 2 unsur B, sedangkan untuk membuat barang jenis II dibutuhkan 3 unsur A dan 2 unsur B. Barang jenis I dijual seharga Rp250.000,00 per unit dan barang jenis II dijual seharga Rp400.000,00 per unit. Agar penjualannya mencapai maksimum, banyak masing-masing barang yang harus dibuat adalah ....

A. 6 jenis I B. 12 jenis II

C. 6 jenis I dan 6 jenis II D. 3 jenis I dan 9 jenis II