4. PERSAMAAN DIFERENSIAL - PERSAMAAN DIFERENSIAL.pdf

Halaman | 1

4. PERSAMAAN DIFERENSIAL

Klasifikasi Persamaan Diferensial  Menyusun Persamaan Diferensial  Persamaan Diferensial Peubah Terpisah  Persamaan Diferensial Koefisien Fungsi Homogen  Persamaan Diferensial Eksak  Persamaan Diferensial Tidak Eksak  Persamaan Diferensial Koefisien Fungsi Linear  oleh : Marwan Persamaan Diferensial Linear Tingkat 2 

Persamaan yang memuat derivatif-derivatif satu atau lebih peubah

bebas terhadap satu atau lebih peubah tak bebas disebut Persamaan

Diferensial (PD). Definisi

4.1. Klasifikasi Persamaan Diferensial

Secara umum, PD dapat dibedakan menjadi 2, yaitu

1. PD Biasa (Ordinary Differential Equations), yaitu PD yang memuat 1 peubah bebas dan 1 peubah tak bebas. PD jenis ini dapat dirumuskan

0

2. PD Parsial (Partial Differential Equations), yaitu PD yang memuat 1 peubah tak bebas dan lebih dari satu peubah bebas. PD jenis ini

dengan dua peubah bebas dapat dirumuskan

0

Selain klasifikasi PD di atas, suatu PD juga dapat dikelompokkan

berdasarkan Tingkat (order) dan Derajat (degree). Tingkat suatu PD adalah tingkat tertinggi dari derivatif-derivatif di dalamnya, sedangkan derajat

Halaman | 2

Klasifikasi lainnya adalah berdasarkan Linear dan Nonlinear. Suatu PD biasa tingkat n disebut linear jika PD tersebut dapat ditulis ke dalam bentuk

( )

( )

( )

a

( )

x y g

( )

x

Selain PD bentuk tersebut adalah PD nonlinear.

Ada banyak permasalahan-permasalahan yang memerlukan PD

misalnya :

- Menentukan gerak proyektil, roket atau planet

- Studi tentang reaksi-reaksi kimia

- Studi tentang gelombang-gelombang pada permukaan membran

- Analisis lendutan balok atau pelat

Pada dasarnya ada dua permasalahan utama di dalam studi Persamaan

diferensial, yaitu : bagaimana menyusun suatu PD dan bagaimana

menyelesaikan PD

menyusun PD

F(x,y,c) = 0 f(x,y, dx dy

) = 0

menyelesaiakan PD

4.2. Menyusun Persamaan Diferensial

Suatu PD dapat muncul dari gejala-gejala fisis yang di-rumuskan secara

Halaman | 3 Misalkan akan ditentukan PD dari persamaan-persamaan berikut :

1. y = mx , m∈R

2. x2_+y2 _{– 2kx = 0 , k} ≥ ₀

1. y = mx ⇒ Penyelesaian :

dx dy

=m , diperoleh :

y=      

dx dy

x y=mx

⇔ y–x dx dy

=0 suatu PD tingkat 1 derajat 1

2. x2 _{+ y}2 _{– 2kx = 0 ...(i)} ⇔ x2 _{+ y}2 _{– 2kx + k}2 _{= k}2

⇔ x2 _{– 2kx + k}2 _{+ y}2 _{= k}2

⇔ (x – k)2 _{+ (y – 0)}2 _{= k}2 _{adalah persamaan lingkaran, pusat}

(k,0), jejari k.

Jika (i) diderivatifkan ke x diperoleh

2x + 2y dx dy

- 2k = 0 x2 _{+ y}2 _{– 2kx = 0}

⇔ x + y dx dy

= k ………... (ii)

Dari (i) dan (ii) diperoleh :

x2 _{+ y}2 _{– 2 (x + y} dx dy

) x = 0

⇔ y2 _{– x}2 _{– 2xy} dx dy

= 0, suatu PD tingkat 1 derajat 1

Menyusun Model PD Lendutan Balok

Halaman | 4 - dari teori elastisitas diketahui

M(x)=bending momen

w(x)=beban pada balok

Di lain pihak, Bending momen adalah ‘lengkungan’ (curvature) dari

lendutan itu sendiri, yaitu

EI = kakakuan lentur (flexural rigidity) balok

untuk y(x) kecil, y’≈0, jadi

sehingga diperoleh :

suatu PD tingkat 4.

Macam-macam penyelesaian PD

1. Penyelesaian Umum / PU (General Solution) yaitu penyelesaian yang memuat konstanta-konstanta sebarang.

2. Penyelesaian Khusus/PK (Particular Solution) yaitu penyelesaian yang tidak memuat konstanta, yang diperoleh dari PU dengan memberi nilai

konstanta-konstanta.

3. Penyelesaian Singular /PS (Singular Solotion) yaitu penyelesaian yang

tidak memuat konstanta tetapi bukan PK.

Selanjutnya akan ditinjau penyelesaian beberapa persamaan diferensial

tingkat 1 derajat 1, dengan bentuk umum:

Halaman | 5 4.3. Persamaan Diferensial Peubah Terpisah

PD (∗) disebut persamaan diferensial peubah terpisah jika dapat ditulis

ke bentuk

g(x) dx + h(y) = 0 ... (1)

PU-nya diperoleh dengan mengintegralkan (1), yaitu

∫

g(x) dx +

∫

h(y) dy = C

Contoh

1. Selesaikan PD : x + y

dx dy

= 0

Jawab :

x + y dx dy

= 0

⇔ x dx + y dy = 0

⇔ ∫x dx + ∫y dy = C ⇔ ½ x2 _{+ ½ y}2 _{= C}

⇔ x2 _{+ y}2 _{= k}2 _{, k = 2 : PU PD C}

2. Selesaikan PD : 1−y2 dx + 1−x2 dy = 0

Jawab

∫

∫

=

− +

− 1 y C

dy x

1 dx

2 2

: ⇔

⇔ sin-1_{x + sin}-1_{y = C}

Misal sin-1_{x =} α _{1 x}

sin-1_{y =} β _α

maka : 2

x

1−

⇔ α + β = C ⇔ sin (α + β) = sin C

⇔ sin α cos β + sin β cos α = sin C

⇔ x ₁−_y2 _{+ y 1}−_x2 _{= k , k = sin C : PU-PD}

Halaman | 6 Maka diperoleh PK :

x 2

y

1− + y 2

x

1− = 1

4.4. Persamaan Diferensial Koefisien Fungsi Homogen

- Fungsi f(x,y) disebut homogen berderajat n dalam x dan y jika

f(λx,λy) = λn _{f(x,y) ,} ∀λ∈ _Rasional.

- PD (∗) disebut PD koefisien fungsi homogen jika M(x,y) dan N(x,y) masing-masing fungsi homogen berderajat sama dalam x & y.

- Penyelesaian PD homogen diperoleh melalui substitusi y = ux atau x = wy , u dan w peubah-peubah baru.

Dengan substitusi tersebut diperoleh PD peubah terpisah.

Contoh :

PD : (x2 _{+ y}2_{) dx – 2xy dy = 0}

Jadi M(x,y) = x2 _{+ y}2 _{, fungsi homogen derajat 2}

N(x,y) = -2xy , fungsi homogen derajat 2

Ambil y = ux ⇒ dy = udx + xdu , maka PD menjadi

(x2 _{+ u}2 _x2_{) dx – 2x (ux)(udx + xdu) = 0}

⇔ (x2 _{+ u}2_x2 _{– 2x}2_u2_{) dx – 2ux}2 _{du = 0} ⇔ (1 – u2_{) x}2 _{dx - 2ux}3 _{du = 0}

⇔ du

u -1

2u -x dx

2 = 0 , PD peubah terpisah

⇔ du C

u -1

2u -x dx

2

∫

∫

=

⇔ ln x + ln (1 – u2_{) = ln K.}

⇔ x (1 –u2_{) = K , u =} x y

⇔ x (1 - _y2 _x2 _{) = K}

Halaman | 7 4.5. Persamaan Diferensial Eksak

- PD (∗) disebut PD eksak jika

Jika F suatu fungsi dua peubah yang mempunyai derivatif parsial

tingkat satu kontinu di dalam suatu domain D, maka diferensial

total fungsi F, dF didefinisikan oleh :

dF(x,y) = dy

Menyelesaikan PD eksak :

Misalkan PU PD (∗) adalah F(x,y) = C , maka :

persamaan (3) diintegralkan terhadap x :

Halaman | 8

Penyelesaian PD eksak dapat juga diperoleh dengan mengelompokkan

suku-suku PD sehingga masing-masing kelompok menjadi diferensial

total eksak suatu fungsi, kemudian diintegralkan. Cara lain

Diperhatikan kembali dua contoh di atas :

Halaman | 9

4.6. Persamaan Diferensial Tidak Eksak

- PD (∗) dikatakan PD tidak eksak jika

- Penyelesaikan PD tidak eksak dapat diperoleh dengan mengalikan (∗) dengan suatu fungsi u yang disebut faktor Integral (Integrating factor), sehingga diperoleh PD eksak yaitu :

u M(x,y)dy + u N(x,y)dy = 0 ... (8)

dengan syarat eksak :

x Mencari faktor integral u

Halaman | 10

Contoh : Selesaikan PD berikut

1. (4xy + 3y2 _{– x) dx + x (x + 2y) dy = 0}

Sehingga diperoleh faktor integral :

u = xdx 2lnx lnx 2

Diperoleh PD eksak :

x2 _{(4xy + 3y}2 _{– x) dx + x}2 _{. x (x + 2y) dy = 0}

⇔ (4x3_{y + 3x}2 _y2 _{– x}3_{) dx + (x}4 _{+ 2x}3 _{y) dy = 0} ⇔ x4_{y + x}3_y2 _{- ¼ x}4 _{= C : PU PD.}

2. M(x,y) = y(x+y+1)

Halaman | 11 

  

 

∂ ∂ ∂ ∂

x N -y M M

1

=

-y 1

dan u e ydy elny y

1

= = ∫ =

PD menjadi PD eksak :

(y2_{x + y}3 _{+ y}2_{) dx + (x}2_{y + 3y}2_{x + 2xy) dy = 0} ⇔ ½ x2_y2 _{+ xy}3 _{+ xy}2 _{= C : PU PD}

4.7. Persamaan Diferensial dengan Koefisien Fungsi Linear

PD (∗) disebut PD dengan koefisien fungsi linear jika :

M(x,y) = a1x + b1y + c1 , fungsi linear dalam x & y

N(x,y) = a2x + b2 y + c2 , fungsi linear dalam x & y

Ada 2 kemungkinan yang terjadi :

1.

2 1

2 1

b b a

a _≠

, maka ∃ titik (h,k) sedemikian hingga :

a1h+b1k+c1 = a2h+b2k+c2 = 0

Ambil substitusi

x = u+h dan y = v+k ... (14)

u & v peubah-peubah baru

diperoleh :

dx=dv dan dy=dv ... (15)

Selanjutnya persamaan (14) dan (15) disubstitusi ke persamaan (∗),

diperoleh :

{a1(u+h)+b1(v+k)+c1}dv+{a2(u+h)+b2(v+k)+c2}dv = 0 ⇔ {a1u+b1v+(a1h+b1k+c1)}du +

{a2u+b2v+(a2h+b2k+c2)}dv = 0

⇔ {a1u+b1v+0}du+{a2u+b2v+0}dv = 0

⇔ (a1u+b1v) du + (a2u+b2v) dv = 0 ... (16)

(16) adalah PD koefisien fungsi homogen dalam u dan v, selanjutnya

Halaman | 12 2.

2 1

2 1

b b a

a ₌

= λ ⇔ a1=λa2 dan b1=λb2

Pada kasus ini dapat diambil substitusi :

w=a2x+b2y ... (17)

maka diperoleh

λw = (λa2)x+(λb2)y = a1x+b1y dan

dw = a2dx+b2dy ⇔ dy= 2

b 1

(dw–a2dx) ... (18)

substitusi (17) dan (18) ke persamaan (∗) menghasilkan

(λw + c1) dx + (w + c2) dy = 0 ⇔ (λw + c1) dx + (w + c2)

2

b 1

(dw – a2 dx) = 0

⇔ b2 (λw + c1) dx + (w + c2) dw – a2 (w + c2) dx = 0

⇔ {b2(λw+c1)–a2(w+c2)}dx+(w+c2)dw = 0 ... (19)

(19) adalah PD peubah terpisah, selanjutnya diselesaikan.

Contoh :

1. (x+2y–4)dx–(2x+y–5)dy=0

Karena

2 1

2 1

b b 1

-2 2

-1 a

a _{= ≠ =}

, maka diambil x=v+h dan y=v+k

h dan k dicari

h + 2k – 4 = 0 × 2 2h + k – 5 = 0 –

3k – 3 = 0 ⇔ k=1 dan h = 2

Sehingga :

x = u+2 ⇒ dx = du

y = v+1 ⇒ dy = dv

diperoleh PD koefisien fungsi homogen :

(u + 2v) du - (2u + v) dv = 0

diselesaikan dengan substitusi

Halaman | 13 du = z dv + v dz

diperoleh :

(zv+2v)(zdv+vdz) - (2zv+v)dv = 0

Penyelesaian :

Karena

diperoleh :

Halaman | 14

Masih banyak jenis persamaan diferensial tingkat 1 yang sudah disusun

teknik penyelesaiannya. Beberapa jenis PD tingkat 1 yang diuraikan di atas

dianggap cukup sebagai dasar bagi mereka yang baru memulai mempelajari

PD. Selanjutnya akan ditinjau beberapa penyelesaian PD tingkat 2 yang

sederhana.

4.8. Persamaan Diferensial Linear Tingkat 2

Bentuk umum Persamaan Diferensial Linear Tingkat 2 yang akan

ditinjau adalah

a0(x) a (x)y

a0, a1 dan a2 masing-masing fungsi konstan, maka (20) disebut PD

Halaman | 15 Secara umum PD tingkat 2 dengan koefisien bukan fungsi konstan

tidak dapat diselesaikan ke dalam bentuk fungsi-fungsi yang diketahui

(eksplisit). Penyelesaian kasus non homogen dilakukan dengan

menyelesaikan bentuk homogen terlebih dahulu, kemudian dilanjutkan

(dengan metode koefisien tak tentu atau metode variasi parameter) mencari

penyelesaian yang bersesuaian untuk bentuk non homogennya.

Ada beberapa teorema penting menyangkut peyelesaian PD tingkat 2

homogen.

Teorema 1

Jika a0, a1 dan a2 masing-masing fungsi kontinu pada interval J, maka

terdapat tepat dua peyelesaian yang bebas linear pada interval J

tersebut.

Teorema 2

Jika y1(x) dan y2(x) penyelesaian PD (20), maka y1 dan y2 bebas linear

bila hanya bila Wronskian mereka tidak nol pada J, yaitu :

Teorema 3

Jika y1(x) dan y2(x) penyelesaian PD (20), c1 dan c2 konstan sebarang,

maka c1y1(x)+c2y2(x) juga penyelesaian PD (20)

PD Linear Tingkat 2 Homogen dengan Koefisien Konstan

Bentuk umum :

ao

dx dy a dx

y d

1 2 2

Halaman | 16 Penyelesaian PD (21) dapat diperoleh dengan substitusi y=emx

diperoleh :

(aom2 _{+ a1m + a2) e}mx _{= 0}

⇔ aom2 _{+ a1m + a2 = 0 , disebut persamaan karakteristik PD}

(21)

⇔ m1,2 =

0

2 1 2 1 1

a 2

a a 4 a

a ± −

−

Jadi y1=_em1x _{dan y2=e}m2x_{, masing-masing merupakan suatu}

penyelesaian PD (21)

Ada beberapa kemungkinan nilai m1 & m2 :

1. Jika m1 = m2 = m , maka PU PD (21) adalah

y = (k1+k2 x) emx _{... (22)}

2. Jika m1 ≠ m2 , maka PU PD (21)

y = k1 _em1x _{+ k2 e}m2x _{... (23)}

3. Jika m1 & m2 bilangan-bilangan kompleks

m1=α+βi dan m2=α−βi

maka PU PD (21) pada prinsipnya sama dengan kasus m1 ≠ m2 di atas.

Hanya saja untuk mendapatkan bentuk yang lebih sederhana dapat

digunakan rumus euler :

i

eβ = cos β + i sin β , i = −1

(rumus euler tersebut dapat dibuktikan dengan substitusi x=βi pada

deret Maclaurin ex_).

Dari rumus euler di atas, diperoleh : i

eα+β =eα(cos β + i sin β), sehingga

PU PD (21) yang diperoleh adalah :

y = eαx _{(k1 cos} β_{x + k2 sin} β_{x) ... (24)}

Halaman | 17 1. y’’ + y’– 2y = 0

Persamaan karakteristik : m2 _{+ m – 2 = 0}

⇔ m1 = 1 atau m2 = -2

maka PU PD : y = k1ex _{+ k2 e}-2x

2. y” – 2y’ + y = 0

Persamaan karakteristik : m2 _{– 2m + 1 = 0} ⇔ _{m1 = m2 = 1}

maka PU PD : y = ex _{(k1 + k2x)}

3. y” + 2y’ + 2y = 0

Persamaan karakteristik : m2 _{+ 2m + 2 = 0}

⇔ m1 = -1 + i atau m2 = -1 – i

maka PU PD :

y = k1 e(-1+i) x _{+ k2 e}(-1–i) x

= k1 e-x _{(cos x + i sin x) + k2 e}-x _{(cos x - i sin x)}

= [(k1 + k2) cos x + (k1 – k2) i sin x ] e-x

= (k1* cos x + k2* sin x) e-x

dengan k1* = k1 + k2 dan k2* = (k1 – k2) i

Kejadian khusus PD (21) adalah :

(a). PD bentuk + dx

y d

2 2

a2 _{y = 0 ... (25)}

Dalam hal ini, diperoleh m1=ai dan m2=-ai, sehingga PU PD (25)

adalah dari persamaan (24) dengan α=0, yaitu :

y = k1 cos x + k2 sin x

(b). PD bentuk − dx

y d

2 2

a2 _{y = 0 ... (26)}

Dalam hal ini, diperoleh m1=a dan m2=-a, sehingga PU PD (26)

adalah dari persamaan (23), yaitu :

y = k1 eax_{+ k2 e}-ax

atau (bentuk alternatif)

Halaman | 18 PD Linear tingkat 2 Non Homogen dengan Koefisien Konstan

Bentuk umum :

ao a y

dx dy a dx

y d

2 1

2 2

+

+ = R(x), dengan R(x) ≠ 0 ... (27)

Penyelesaian umum PD (27) diperoleh sebagai berikut

PU PD (27) = PU PD(21) + PK PD (27) ⇔ y = yc + yp

∗ yc ialah PU PD (21) dan disebut fungsi komplementer

(complementary function)

∗ yp ialah PU PD (21) dan disebut integral khusus (Particular Integral)

Ada beberapa metode mencari Integral khusus, salah satunya adalah Metode

Koefisien Tak Tentu.

Metode koefisien tak tentu pada dasarnya adalah mengambil yp sebagai

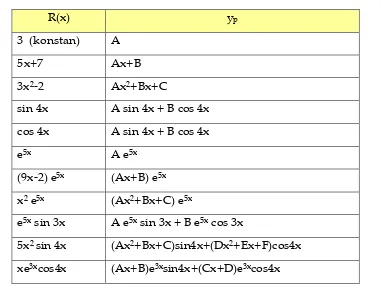
bentuk umum dari R(x). Tabel berikut memuat beberapa bentuk yp yang

bersesuaian dengan R(x).

Tabel

R(x) yp

3 (konstan) A

5x+7 Ax+B

3x2_{-2 Ax}2_+Bx+C

sin 4x A sin 4x + B cos 4x

cos 4x A sin 4x + B cos 4x

e5x _{A e}5x

(9x-2) e5x _{(Ax+B) e}5x

x2 _e5x _(Ax2_{+Bx+C) e}5x

e5x _{sin 3x A e}5x _{sin 3x + B e}5x _{cos 3x}

5x2 _{sin 4x (Ax}2_{+Bx+C)sin4x+(Dx}2_+Ex+F)cos4x

Halaman | 19 Contoh :

Selesaikan PD : y” – 5y’ + 6y = 5 sin x

Penyelesaian :

- Mencari yc

Persamaan karakteristik m2_–5m+6=0 ⇔ _{m1=2 , m2=3}

Diperoleh yc = k1 e2x _{+ k2 e}3x

- Mencari yp

Karena R(x)= 5 sin x, maka dapat diambil

yp = A sin x + B cos x

p

y′ = A cos x – B sin x

p

y′′= - A sin x – B cos x

disubstitusi ke PD , diperoleh

p

y′′–5yp′ +6 yp = 5 sin 4x

⇔ (5A + 5B) sin x + (-5A + 5B) cos x = 5 sin 4x ⇔ 5A + 5B = 5 dan -5A + 5B = 0

⇔ A = ½ dan B = ½

Diperoleh yp = ½ sin x + ½ cos x

Jadi PU PD :

y = yc + yp = k1 e2x _{+ k2 e}3x _{+ ½ sin x + ½ cos x}

Kadang-kadang dijumpai ada suku yp yang sama dengan suku yc. Pada

keadaan ini maka yp harus dikalikan dengan xn_{, dengan n bulat positif}

terkecil sedemikian hingga tidak terdapat suku yp yang sama dengan suku

yc.

Contoh

Selesaikan PD : y” – 2y’ + y = ex

Halaman | 20 - Mencari yc

Persamaan karakteristik m2_–2m+1=0 ⇔ _m1=m2=1

Diperoleh yc = k1ex _{+ k2xe}x

- Mencari yp

Karena R(x)=ex_{, maka menurut tabel di atas dapat diambil yp=Ae}x_.

Tetapi pengambilan tersebut mengakibat-kan adanya suku yang

sama dengan suku yc . Demikian juga halnya jika diambil

yp=Axex_{. Jadi bentuk yang dapat diambil adalah}

yp=Ax2_ex

p

y′ =2Axex_+Ax2_ex

p

y′′=2Aex_+4Axex_+Ax2_ex

Substitusi ke PD diperoleh A=½ ⇒ yp=½ x2_ex