VEKTOR-VEKTOR di BIDANG DAN di RUANG

(1)

VEKTOR-VEKTOR di BIDANG DAN di RUANG

1. Ruang-2 Dan Ruang-3

Vektor didefinisikan sebagai besaran yang memiliki arah. Kecepatan, gaya dan pergeseran merupakan contoh – contoh dari vektor karena semuanya memililiki besar dan arah walaupun untuk kecepatan arahnya hanya positif dan negatif. Vektor-vektor dalam dinyatakan secara geometris sebagai segmen-segmen garis yang terarah atau panah-panah di dalam ruang-2 atau ruang-3. Jika vektor bearada di R2 maka dikatakan vektor berada di bidang, sedangkan jika vektor

berada di R3 maka dikatakan vektor berada di ruang. Arah panah menentukan arah vektor dan panjang panah menyatakan besarnya.

Komponen Dan Panjang Vektor

Elemen-elemen dari pada vektor biasanya disebut komponen-komponen dan sebagai notasinya biasa dipakai huruf latin kecil (misalnya komponen x1, x2, x3, x4 untuk n = 4) sedangkan

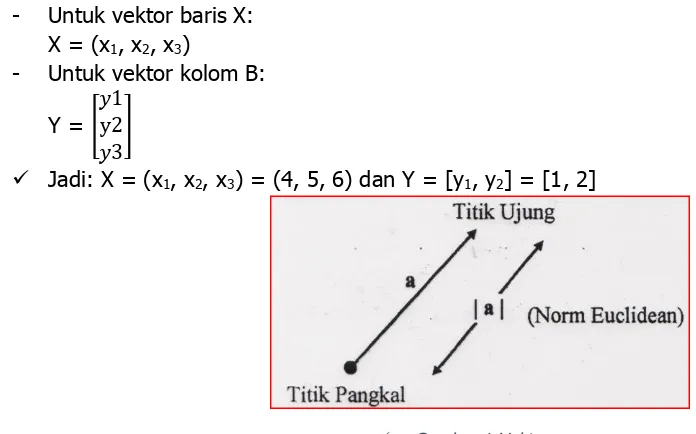
untuk vektornya dipakai huruf latin besar (A, K, V); kecil tebal (a, k, v, w, x); atau huruf kecil dengan ruas garis 𝑎̅. Panjang vector disimbolkan dengan | |, contohnya |a|. Secara geometri vektor memiliki titik pangkal/awal/permulaan (initial point) dan titik ujung/akhir/terminal (terminal point).

Apabila diperhatikan, maka vektor tidak lain daripada matirx yang terdiri dari satu baris dan n kolom untuk vektor baris dan terdiri dari satu kolom dan n baris untuk vektor kolom, yaitu sebagai berikut:

- Untuk vektor baris X: X = (x1, x2, x3)

- Untuk vektor kolom B: Y = [

𝑦1 y2 𝑦3]

 Jadi: X = (x1, x2, x3) = (4, 5, 6) dan Y = [y1, y2] = [1, 2]

(2)

Visualisasi Vektor

 Vektor a dan b dikatakan sama, jika Arah kedua vektor sama dan |a| = |b|

 Vektor a dan b dikatakan tidak sama, jika Arah kedua vektor tidak sama, meskipun |a| = |b|

 Vektor a dan b dikatakan tidak sama, jika Arah kedua vektor tidak sama dan |a| ≠ |b|

Vektor dalam sistem koordinat kartesian

1. Koordinat kartesian dua dimensi

a. Gambar vektor m (3,-2) dalam sumbu koordinat dengan pangkal vektor di (0,0) !!

(3)

2. Koordinat kartesian tiga dimensi Gambar vektor b (-2, 5, 1) dengan pangkal a (3, 4, 7)

Panjang Vektor

1. Panjang vektor a yang berpangkal pada (0,0) didefinisikan sebagai:

Disebut sebagai vektor nol, jika |a|=0 yang berarti a1=a2=0 Contoh :

Cari panjang vektor a (5,-3) !

2. Panjang vektor a (x2, y2, z2) dan berpangkal pada (x1, y1, z1) didefinisikan sebagai:

Contoh :

Cari panjang vektor a (5,-3,1) dengan titik pangkal (1,1,1) Gambar vektor b (-2, 5, 1) dengan pangkal a (3, 4, 7)!

LATIHAN 1

1. Gambarkan dalam satu koordinat, vektor-vektor berikut :

6 36 9

25 )

3 ( 5 |

|a  2  2    

2 4 32 0 16 16 ) 1 1 ( ) 1 3 ( ) 1 5 ( |

(4)

a. s (5,-4) dengan titik pangkal (0,0) b. g (2,1) dengan titik pangkal (-3,-2) c. j (-3,2) dengan titik pangkal (5,-2) d. m (3,2,1) dengan titik pangkal (1,2,1) e. b (3,-2,-1) dengan titik pangkal (-1,1,-3)

2. Cari panjang dari masing2 vektor yang ada pada soal no 1

2. OPERASI DENGAN VEKTOR

1. Penjumlahan dan pengurangan Vektor

Metode penjumlahan dan pengurangan vektor a. Cara Segitiga

Jumlahan 2 vektor a dan b adalah suatu vektor c yang berawal dari titik pangkal vektor a menuju ujung vektor b, setelah ujung vektor a ditempelkan dengan pangkal vektor b.

b. Cara Jajaran Genjang

Untuk memperoleh hasil vektor penjumlahan dari vektor a dan b, maka vektor a dan b harus diposisikan pada 1 titik dan masing-masing vektor diproyeksikan sehingga menghasilkan 1 titik potong antar kedua vektor. Vektor hasil dihubungkan dari titik awal dan titik potong akhir.

Penjumlahan dan pengurangan dari dua buah vektor a dan b, dimana A = (a1, a2, a3) dan B = (b1, b2, b3)

maka C = ai ± bj

contoh: A = (a1, a2) = (3, 5)

(5)

1) C = A + B = (a1 + b1, a2 + b2) = (3 + 1, 5 + 4) = (4, 9)

2) C = A - B = (a1 - b1, a2 - b2) = (3 – 1, 5 – 4) = (2, 1)

Sifat Penjumlahan Vektor

a. a + b = b + a komutatif

b. ( u + v ) + w = u + ( v + w ) asosiatif

c. a + 0 = 0 + a = a elemen netral

d. a + (-a) = 0 elemen invers

2. Perkalian Vektor

a. Perkalian vektor dengan skalar

Apabila vektor X dikalikan dengan suatu skalar, maka X.k = k.X

Contoh:

X = [2, 3, 1] dan k = 2 X.k = 2 [2, 3, 1]= 4, 6, 2 b. Perkalian vektor dengan vektor

Dua buah vektor bisa dikalikan apabila jumlah kolom vektor sebelah kiri sama dengan jumlah baris vektor sebelah kanan.

Contoh: X = ( 1, 2, 3) Y = ( 3, 4, 5)

X’Y = [12 3]

( 3, 4, 5 ) = [_{6 8 10}3 4 5 9 12 15]

, suatu matrix

XY’ = ( 1, 2, 3 ) [34 5]

= 3 + 8 + 15 = 26, suatu skalar

c. Perkalian Vektor dengan Matrix X = ( x1, x2, ... , xn)

B = [𝑎11 𝑎12 … 𝑎1𝑛_{𝑎21 𝑎22 … 𝑎2𝑛} 𝑎𝑛1 𝑎𝑛2 … 𝑎𝑛𝑛]

X.B hanya bisa dilakukan apabila jumlah baris dari matrix itu sama dengan banyakanya jumlah komponen dari vektor tersebut (jumlah kolom). 3. Perkalian Titik dan Perkalian Silang vektor satuan

(6)

Diketahui dua vektor 𝑎̅ = a1, a2, a3 dan 𝑏̅ = b1, b2, b3. Perkalian titik dua vektor

tersebut didefinisikan sebagai:

𝑎̅. 𝑏̅= a1 b1 + a2 b2 + a3 b3

Perkalian Silang (Cross Product)

Hasil perkalian silang diantara dua vektor 𝑎̅ dan 𝑏̅ adalah sebuah vektor lain 𝑐̅. Arah dari 𝑐̅ sebagai hasil perkalian vektor 𝑎̅ dan 𝑏̅ didefinisikan tegak lurus pada bidang yang dibentuk oleh 𝑎̅ dan 𝑏̅. Pada perkalian vektor ini ada ketentuan sebagai berikut :

i x i = 0 i x j = k j x i = -k j x j = 0 j x k = i k x j = -i k x k = 0 k x i = j i x k = -j

Contoh:

Tentukan perkalian titik dan silang dari vektor berikut: X = 2i – 2j + 4k

Y = i – 3j + 2

Perkalian Titik

X . Y = 2.1 + (-2)(-3) + 4.2 = 16

Perkalian Silang

X.Y =

= { (-2).2 – 4.(-3)} i – {2.2 – 4.1} j + {2.(-3) – (-2).1} k = (-4+12) i – (4-4) j + (-6+2) k

= 8i – 0j – 4k = 8i – 4k LATIHAN 2

1. Diketahui vektor A=(3, 4, 12), B=(-4, 3, 0) dan C=(1, 2, 1) Tentukan:

a. |A| b. |B| c. A+B-C d. |A+B-C| e. -3A f. |-3A|

g. Nilai x sehingga -3A+B+x=4x+C

2. Tentukan perkalian titik dan perkalian silang vektor berikut: a. A = 4i + 3j − 2k dan B = 7i + 2j + 5k

2

3

1

2 -

-

2

4 k

j

i

(7)

3. KOMBINASI LINEAR, BEBAS LINEAR dan BASIS

Kombinasi Linear

jika 𝑎̅ = (a1, a2, a3) dapat dinyatakan dengan 𝑎̅ = a1 𝑢̅ + a2 𝑣̅ + a3 𝑤̅. Dalam hal ini kita

sebut bahwa vektor 𝑎̅dapat disajikan dalam kombinasi linear dari tiga vektor 𝑢̅, 𝑣̅ dan 𝑤̅.

Secara umum, misalkan diketahui vektor 𝑢̅1, 𝑢̅2, 𝑢̅3, ... , 𝑢̅n dan vektor 𝑎̅. Vektor 𝑎̅dapat

disebut kombinasi linear dari vektor 𝑢̅1, 𝑢̅2, 𝑢̅3, ... , 𝑢̅n, jika terdapat bilangan s1, s2, sn

(bilangan skalar), sehingga berlaku:

𝑎̅ = s1 𝑢̅1 + s2 𝑢̅2 + .... + sn 𝑢̅

Contoh:

Diketahui vektor U = ( 2, -1, 3) dan V (-1, 5, -2). Jika mungkin tuliskan vektor A (4, 7, 5) sebagai kombinasi linear dari vaktor U dan V!

Jawab Dengan eliminasi Gauss

(1 0 30 1 2

berikut merupakan kombinasi linear dari vektor-vektor U dan V! a) A = ( 4, 2, 6 )

b) B = ( 1, 5, 6 ) c) C = ( 0, 0, 0 ) Jawaban

a) Tulis

k

₁

u



k

₂

v



a

. Akan diperiksa apakah ada k1, k2, sehingga kesamaan tersebut

dipenuhi. Tulis

(8)

dengan OBE, diperoleh:

dengan demikian A merupakan kombinasi linear dari U dan V atau ditulis

A=U + 2 V

b) tulis

k

₁

u





k

₂

v





b



. Akan diperiksa apakah ada k1, k2, sehingga kesamaan tersebut

dipenuhi. Tulis



dapat ditulis menjadi



Baris terakhir pada matriks ini menunjukkan bahwa SPL tersebut adalah tidak konsisten (tidak mempunyaisolusi). Jadi, tidak ada nilai k1 dan k2 yang memenuhi

 b tidak dapat dinyatakan sebagai kombinasi linear dari u dan v

c) Dengan memilih k1 = 0 dan k2 = 0, maka dapat ditulis

k

u



k

v



c



2

1 .

artinya vektor nol merupakan kombinasi linear dari vektor apapun

(9)

Bebas Linear

Kumpulan vektor {

𝑢̅

1

,

𝑢̅

2

,

𝑢̅

3

, ... ,

𝑢̅

n

} disebut kumpulan bebas linear jika persamaan:

s

1

𝑢̅

1

+ s

2

𝑢̅

2

+ .... + s

n

𝑢̅

= 0

hanya diperoleh jika s1 = s2 = ... = sn = 0. Jika skalar s1 , s2 , ... sn salah satunya tidak 0,

maka vektor tersebut bergantung linear. Contoh

a) Diketahui vektor 𝑢̅1 = ( 1, 0 ) dan 𝑢̅2 (1, 1). Buktikan bahwa vektor {𝑢̅1 , 𝑢̅2 } adalah

bebas linear! Jawab

Harus memenuhi persamaan

s1 𝑢̅1 + s2 𝑢̅2 = 0 atau s1 (1, 0) + s2 (1, 1)= 0

dengan operasi vektor dapat ditulis (s1 + s2, s2) = (0, 0).

Karena s2 = 0 dan juga s1 = 0, maka kumpulan vektor {𝑢̅1 , 𝑢̅2 } adalah bebas linear.

b) Diketahui vektor 𝑢̅1 = ( 1, 2, 4 ), 𝑢̅2 = ( 2, 2, 8 ) dan 𝑢̅3 =(1, 0, 4). Apakah vektor

{𝑢̅1 , 𝑢̅2 , 𝑢̅3 } bebas linear?

Jawab

Harus memenuhi hubungan berikut: s1 𝑢̅1 + s2 𝑢̅2 + s3 𝑢̅3= 0

s1 (1, 2, 4) + s2 (2, 2, 8) + s3 (1, 0, 4)= 0 atau s1[

1 2 4]

+ s2 [

2 2

8] + s3 [ 1 0 4] = [

0 0 0] akan diperoleh 3 persamaan:

s1 + 2s2+ s3 = 0 (1)

2s1 + 2s2+ 0= 0 (2)

4s1 + 8s2+ 4s3 = 0 (3)

Dengan jalan subtitusi: 𝑠1 + 2𝑠2 + 𝑠3 = 0 (1) 2𝑠1 + 2𝑠2 + 0 = 0 (2)

−𝑠1 + 0 + 𝑠3 = 0 𝑠1 = 𝑠3

−

4s1 + 8s2+ 4s3 = 0 (3)

4s3 + 8s2+ 4s3 = 0

8s2= -8s3

s2 = -s3

 Jadi, karena tidak semua sklar nilainya = 0, maka vaktor set vaktor {𝑢̅1 , 𝑢̅2 , 𝑢̅3 }

merupakan bergantung linear. Penyelesaian dengan OBE

Nilai s1 bergantung dengan s3

(10)

Matriks lengkap (1 2 1 0_{2 2 0 0} 4 8 4 0)

dengan eliminasi gauss didapat (1 0 −1 0_{0 1} ₁ ₀

0 0 0 0)

Dengan subtitusi diperoleh s2 + s3 = 0, berarti s2= -s3 s1 – s3= 0, berarti s1 = s3 LATIHAN 4:

1. tentukan apakah vektor-vektor dari Rn _{berikut, bebas atau tidak bebas linear!}

𝑢̅1 = [ 1 2 −1

2

] 𝑢̅2 = [ −2 −5 3 0

] 𝑢̅3 = [ 1 0 1 10

]

2. Diketahui vektor 𝑢̅1 = ( -1, 0, 1 ), 𝑢̅2 = ( -2, 1, 1 ) dan 𝑢̅3 =(2, 3, 1). Apakah vektor {𝑢̅1 2, 𝑢̅2 , 𝑢̅3 } bebas linear?

Jawaban

1. ₍

1 −2 1 0

2 −5 0 0

−1 3 1 0

2 0 10 0

) 𝑑𝑒𝑛𝑔𝑎𝑛 𝑂𝐵𝐸 (

1 0 5 0 0 1 2 0 0 0 0 0 0 0 0 0 )

karena nilai k1, k2 dan k3 tidak sama 0 maka vektor tersebut tidak bebas linear

2. (−1 −2 2 00 1 3 0

1 1 1 0) 𝑑𝑒𝑛𝑔𝑎𝑛 𝑂𝐵𝐸 (

1 0 0 0 0 1 0 0 0 0 1 0)

karena nilai k1 = k2 = k3 = 0 maka vektor tersebut adalah bebas linear

Basis dan Dimensi

Jika V adalah sembarang ruang vektor dan S = { ū1, ū2, … , ūn} merupakan himpunan

berhingga dari vektor – vektor di V, maka S dinamakan basis bagi V.

Jika kedua syarat berikut dipenuhi :

• S membangun V

• S bebas linear

Tunjukan bahwa himpunan matriks berikut :

merupakan basis bagi matriks berukuran 2 x 2

    

  

   

      

 

 

 

  

  

 

  

 

 

2 1

0 1 , 4 12

8 0 , 0 1

1 0 , 6 3

6 3

(11)

Jawab :

Tulis kombinasi linear :

Atau

dengan menyamakan setiap unsur pada kedua matriks, diperoleh SPL :

Determinan matriks koefisiennya (MK) = 48

• det(MK)  0  SPL memiliki solusi untuk setiap a,b,c,d

Basis untuk setiap ruang vektor adalah tidak tunggal. Contoh :

(12)

Contoh :

Diberikan SPL homogen : 2p + q– 2r– 2s = 0

p– q + 2r– s = 0 –p + 2q – 4r + s = 0 3p – 3s = 0

Tentukan basis ruang solusi dari SPL diatas Jawab :

SPL dapat ditulis dalam bentuk :



dengan melakukan OBE diperoleh :



Solusi SPL tersebut adalah

b

dimana a dan b adalah parameter Jadi, basis ruang solusi dari SPL diatas adalah :

