I. Tujuan Pembelajaran
Setelah mempelajari bab ini, peserta didik diharapkan mampu membaca dan menyajikan data dalam bentuk tabel distribusi dan histogram, mendeskripsikan serta menghitung berbagai ukuran pemusatan, ukuran letak, dan ukuran penyebaran, serta menerapkan konsep-konsep tersebut dalam menyelesaikan masalah. Dengan demikian, siswa dapat bersikap cermat dalam menganalisis setiap permasalahan.
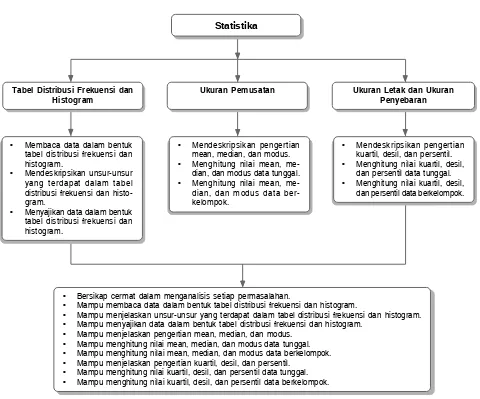
II. Statistika
Statistika mencakup berbagai teknik untuk membaca data dalam bentuk tabel distribusi frekuensi dan histogram. Peserta didik diajarkan untuk mendeskripsikan unsur-unsur dalam tabel distribusi frekuensi dan histogram, serta menyajikan data dalam format tersebut. Ini merupakan langkah awal untuk memahami data secara visual.
2.1. Tabel Distribusi Frekuensi dan Histogram
Peserta didik belajar untuk menyajikan data dalam bentuk tabel distribusi frekuensi dan histogram. Mereka diajarkan untuk menjelaskan unsur-unsur yang terdapat dalam tabel distribusi frekuensi dan histogram, serta cara menyajikan data secara efektif.
III. Ukuran Pemusatan, Ukuran Letak, dan Ukuran Penyebaran
Dalam bagian ini, peserta didik belajar tentang ukuran pemusatan seperti mean, median, dan modus, serta ukuran letak dan penyebaran. Mereka diajarkan untuk menghitung nilai-nilai ini dari data tunggal maupun data berkelompok, yang merupakan keterampilan penting dalam analisis data.
3.1. Ukuran Pemusatan
Peserta didik mempelajari pengertian dan cara menghitung mean, median, dan modus dari data tunggal dan data berkelompok. Pengertian ini penting untuk memahami bagaimana data dapat dikelompokkan dan dianalisis.
3.2. Ukuran Letak dan Penyebaran
Peserta didik juga belajar tentang kuartil, desil, dan persentil. Mereka diajarkan untuk menghitung nilai-nilai ini baik dari data tunggal maupun data berkelompok, yang membantu dalam memahami distribusi data.
IV. Latihan dan Aktivitas
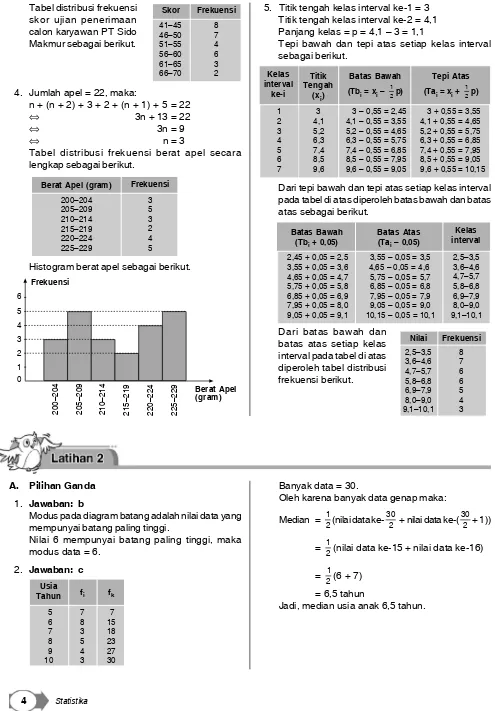
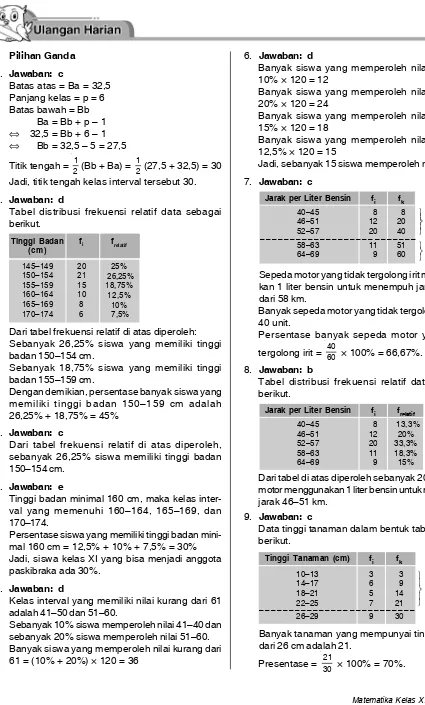
Bagian ini berisi latihan soal yang dirancang untuk membantu peserta didik menerapkan konsep yang telah dipelajari. Latihan ini mencakup soal pilihan ganda dan uraian yang menguji pemahaman peserta didik terhadap materi statistika dan analisis data.
4.1. Pilihan Ganda
Soal pilihan ganda dirancang untuk menguji pemahaman konsep dasar statistika dan penerapannya dalam situasi nyata. Peserta didik diminta untuk memilih jawaban yang paling tepat berdasarkan pengetahuan mereka.
4.2. Uraian
Soal uraian memberikan kesempatan kepada peserta didik untuk menjelaskan langkah-langkah penyelesaian masalah secara rinci. Hal ini membantu mereka untuk lebih memahami proses analisis data dan penerapan konsep statistika.
V. Referensi dan Sumber Tambahan
Di akhir materi, terdapat referensi dan sumber tambahan yang disarankan untuk pembelajaran lebih lanjut. Sumber-sumber ini dapat membantu peserta didik untuk memperdalam pemahaman mereka mengenai statistika dan analisis data.
Referensi Dokumen
- Buku Matematika SMA/MA Kelas XI ( Kementerian Pendidikan dan Kebudayaan Republik Indonesia )
- Buku Guru Matematika SMA/MA Kelas XI ( Kementerian Pendidikan dan Kebudayaan Republik Indonesia )
- Buku PR Matematika Kelas XIB ( PT Intan Pariwara )
- Buku PG Matematika Kelas XIB ( PT Intan Pariwara )