BAB II
LANDASAN TEORI
2.1 Pengertian Dasar Teori Antrian
Dalam kehidupan sehari-hari, antrian (queueing) sangat sering ditemukan. Mengantri sering harus dilakukan jika kita menunggu giliran misalnya mengambil atau menyetor uang ke bank. Antrian juga dapat terjadi pada barang misalnya antrian bahan mentah yang akan diproses untuk dijadikan produk jadi pada usaha manufaktur, ataupun data yang akan diolah di pusat komputer.
Teori antrian pertama kali dikemukan oleh A.K.Erlang, seorang insinyur denmark yang bekerja di Copenhagen Telephone. Tahun 1909 Saat itu, Permintaan hubungan telepon ke satu nomor masih dilayani secara manual oleh operator dimana pada saat sibuk peminta harus menunggu untuk bisa disambungkan dengan nomor yang dikehendaki karena padatnya lalu lintas komunikasi. Teori ini telah diperluas penerapannya ke masalah umum dengan memasukkan faktor antri dan garis tunggu, yakni suatu garis tunggu pelanggan yang memerlukan layanan dari sistem yang ada.
Untuk mempertahankan pelanggan, sebuah organisasi selalu berusaha untuk memberikan pelayanan yang terbaik. Pelayanan yang terbaik tersebut diantaranya adalah memberikan pelayanan yang cepat sehingga pelanggan tidak dibiarkan menunggu (mengantri) terlalu lama. Namun demikian, dampak pemberian layanan yang cepat ini akan menimbulkan biaya bagi organisasi, karena harus menambah fasilitas layanan. Oleh karena itu, layanan yang cepat akan sangat membantu untuk mempertahankan pelanggan, yang dalam jangka panjang tentu saja akan meningkatkan keuntungan bagi organisasi tersebut.
berarti diasumsikan bahwa ciri-ciri operasi seperti panjang antrian dan rata-rata waktu menunggu akan memiliki nilai konstan setelah berjalan selama satu periode waktu.
2.2 Sistem Antrian
Sistem antrian adalah kedatangan pelanggan untuk mendapatkan pelayanan, menunggu untuk dilayani jika fasilitas pelayanan (server) masih sibuk, mendapatkan pelayanan dan kemudian meninggalkan sistem setelah dilayani. Pelanggan tiba dengan waktu tetap atau tidak tetap untuk memperoleh pelayanan pada fasilitas pelayanan. Bila pelanggan yang tiba dapat masuk kedalam fasilitas pelayanan, maka pelayanan akan segera dilakukan. Tetapi kalau harus menunggu, maka mereka akan membentuk suatu antrian hingga tiba waktunya untuk dilayani. Mereka akan dilayani dengan waktu tetap atau tidak tetap. Dan setelah selesai, mereka pun meninggalkan antrian (Gross, 2001).
Berdasarkan uraian diatas, maka sistem antrian dapat dibagi menjadi 2 komponen yaitu :
a. Antrian yang memuat pelanggan atau satuan-satuan yang memerlukan pelayanan (pembeli, orang sakit, mahasiswa, kapal dan lain-lain). b. Fasilitas pelayanan yang memuat pelayanan dan saluran pelayanan
(Pompa minyak dan pelayanannya, loket bioskop, petugas penjual karcis, teller, dan lain-lain).
Secara garis besar, sistem antrian dapat diklasifikasikan menjadi sistem yang berbeda-beda dimana teori antrian dan simulasi sering diterapkan secara luas. Klasifikasi menurut Hillier dan Lieberman (2001) adalah sebagai berikut:
1. Sistem pelayanan komersial, merupakan aplikasi yang sangat luas dari model antrian, seperti restoran, kafetaria, toko-toko, salon, butik, dan supermarket.
3. Sistem pelayanan transportasi
4. Sistem pelayanan sosial, merupakan sistem-sistem pelayanan yang dikelola oleh kantor-kantor lokal maupun nasional, seperti kantor tenaga kerja, kantor pos, rumah sakit, puskesmas dan lain lain.
2.2.1 Faktor dan Elemen dalam Sistem Antrian
Elemen utama dari antrian yaitu: sumber (populasi), kedatangan pelanggan, barisan antrian, disiplin pelayanan, dan mekanisme pelayanan. Karakteristik setiap elemen ini akan memberi bentuk sistem antrian.
2.2.1.1 Sumber
Kumpulan orang atau barang dari mana datang atau dipanggil untuk memperoleh pelayanan disebut sumber. Menurut ukurannya, populasi yang akan dilayani bisa terbatas (finite) dan tidak terbatas (infinite). Ukuran populasi dikatakan terbatas apabila jumlah anggota dari populasi relatif kecil atau dapat dihitung. Contohnya jumlah mahasiswa yang antri untuk registrasi di sebuah perguruan tinggi sudah diketahui jumlahnya. Ukuran populasi tidak terbatas apabila jumlah anggota yang cukup besar atau tidak diketahui secara persis karena jumlahnya yang cukup besar. misalnya jumlah pasien yang berkunjung ke rumah sakit.
2.2.1.2 Kedatangan Pelanggan
dapat ditentukan melalui dua cara yaitu kedatangan per satuan waktu dan distribusi waktu antar kedatangan.
2.2.1.3 Barisan Antrian
Suatu antrian selalu ditandai dari besarnya jumlah pelanggan yang ada dalam sistem antrian untuk mendapatkan pelayanan. Barisan antri tergantung dari kapasitas sistem, jumlah maksimum dari pelanggan yang dapat ditampung oleh sistem dapat terbatas atau tidak terbatas. Antrian disebut terbatas apabila jumlah pelanggan yang dibenarkan masuk ke dalam sistem antrian dibatasi sampai jumlah tertentu. Bila pembatasan jumlah tidak ada, maka antrian tersebut disebut tidak terbatas.
2.2.1.4 Disiplin Pelayanan
Disiplin pelayanan adalah suatu aturan dimana para pelanggan dilayani, atau disiplin pelayanan (service discipline) yang memuat urutan para pelanggan menerima layanan. Disiplin antrian adalah konsep membahas mengenai kebijakan dimana para pelanggan dipilih dari antrian untuk dilayani, berdasarkan urutan kedatangan pelanggan. Ada 4 bentuk disiplin pelayanan yang biasa digunakan dalam praktek yaitu :
1. First come first served (FCFS) atau first in first out (FIFO), suatu peraturan dimana yang akan dilayani ialah pelanggan yang datang terlebih dahulu. Contohnya seperti pada pada antrian di loket-loket penjualan karcis kereta api.
3. Service in random order (SIRO) atau pelayanan dalam urutan acak atau sering dikenal juga random selection for services (RSS), artinya pelayanan atau panggilan didasarkan pada peluang secara random, tidak soal siapa yang lebih dahulu tiba. Contohnya ialah pada arisan, dimana pelayanan dilakukan secara random.
4. Priority service (PS) artinya, prioritas pelayanan diberikan kepada mereka yang mempunyai prioritas paling tinggi dibandingkan dengan mereka yang memiliki prioritas paling rendah, meskipun yang terakhir ini sudah lebih dahulu tiba dalam garis tunggu. Kejadian seperti ini bisa disebabkan oleh beberapa hal, misalnya seseorang yang keadaan penyakit yang lebih berat dibanding dengan orang lain dalam sebuah rumah sakit.
2.2.1.5 Mekanisme Pelayanan
Mekanisme pelayanan terdiri dari satu atau lebih fasilitas pelayanan yang dipasang serial. Setiap fasilitas dapat mempunyai satu atau lebih stasiun pelayanan paralel. Jika sistem mempunyai lebih dari satu fasilitas pelayanan maka pelanggan akan menerima pelayanan secara serial yaitu harus melewati serangkaian pelayanan lebih dahulu baru boleh meninggalkan sistem. Jika sistem mempunyai lebih dari satu pelayanan yang paralel maka beberapa pelanggan dapat dilayani secara simultan.
Atas dasar sifat proses pelayanannya, dapat diklasifikasikan fasilitas-fasilitas pelayanan dalam susunan saluran atau channel (single dan multiple) dan
Ada 4 model struktur antrian dasar yang umum terjadi dalam sebuah sistem antrian yaitu:
1. Single Channel - Single Phase
Hanya ada satu jalur untuk memasuki sistem pelayanan atau ada satu fasilitas pelayanan dan hanya ada satu stasiun pelayanan atau sekumpulan tunggal operasi yang dilaksanakan. Setelah menerima pelayanan, individu langsung keluar dari sistem. Contoh untuk model sistem ini adalah seorang tukang cukur, seorang pelayan toko, dan sebagainya. Model single channel - single pha se seperti pada Gambar 2.1.
Antrian Pelayan Gambar 2.1 Single Channel – Single Phase
2. Single Channel – Multi Phase
Istilah multi phase menunjukkan ada dua atau lebih pelayanan yang dilaksanakan secara berurutan dalam phase-phase. Sebagai contoh, lini produksi massa, pencucian mobil, tukang cat mobil dan sebagainya. Model single channel-multi phase seperti pada Gambar 2.2.
Antrian Pelayan
Gambar 2.2 Single Channel- Multi Phase
3. Multi Channel - Single Phase
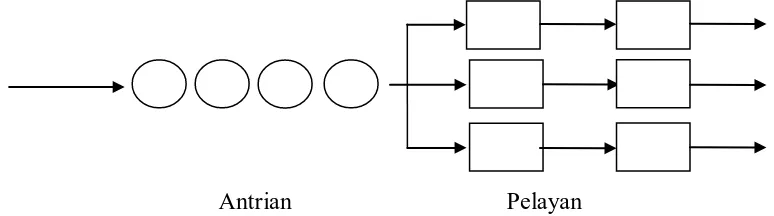
dilayani lebih dari satu loket pelayanan, nasabah yang dilayani lebih dari satu orang teller dan lain sebagainya. Model multi channel -single phase seperti pada Gambar 2.3.
Antrian Pelayan
Gambar 2.3 Multi Channel-Single Phase 4. Multi channel –Multi phase
Pada umumnya, jaringan antrian ini terlalu kompleks untuk dianalisa dengan teori antrian. Teknik simulasi lebih sering digunakan untuk menganalisa sistem ini. Sebagai contoh, registrasi para mahasiswa pada universitas, pelayanan pada pasien di rumah sakit dari pendaftaran, diagnosa, penyembuhan sampai pembayaran. Model Multi Channel–Multi Phase seperti pada Gambar 2.4
Antrian Pelayan
Gambar 2.4 Multi Channel–Multi Phase
2.2.2 Waktu Pelayanan
keadaan sebenarnya. Waktu yang dibutuhkan untuk melayani bisa dikategorikan sebagai konstan dan acak. Waktu pelayanan konstan, jika waktu yang dibutuhkan untuk melayani sama untuk setiap pelanggan. Sedangkan waktu pelayanan acak, jika waktu yang dibutuhkan untuk melayani berbeda-beda untuk setiap pelanggan.
2.3 Model –Model Antrian
Karakteristik dan asumsi dari model antrian dirangkum dalam bentuk notasi. Notasi standar yang digunakan adalah sebagai berikut :
( a / b / c / d / e )
Di mana simbol a, b, c, d, e merupakan elemen dasar dari model antrian :
a = Bentuk distribusi kedatangan yaitu jumlah kedatangan per satuan waktu b = Bentuk distribusi waktu pelayanan yaitu selang waktu antara
satuan-satuan yang dilayani
c = Jumlah fasilitas pelayanan dalam sistem d = Disiplin pelayanan
e = Jumlah maksimum yang diperkenankan berada dalam sistem (dalam pelayanan ditambah yang di garis tunggu).
Untuk huruf a dan b, kita gunakan kode-kode berikut sebagai pengganti:
M = Distribusi kedatangan Poisson atau distribusi pelayanan eksponensial D = Antar kedatangan atau waktu pelayanan tetap
G = Distribusi umum kedatangan atau waktu pelayanan Untuk huruf d dipakai kode-kode pengganti:
FIFO atau FCFS = First-in, first-Out atau First-Come First –Served LIFO atau LCFS = Last in First-Out atau Last-Come First-served SIRO = Service In Random Order
GD = Genaral service Discplint
Misalnya, kalau kita tulis model (M/M/1) : FIFO///), ini berarti bahwa model menyatakan kedatangan didistribusikan secara Poisson, waktu pelayanan didistribusikan secara eksponensial, pelayanan adalah satu atau seorang, disiplin antrian adalah first-in first-out, tidak berhingga jumlah langganan boleh masuk dalam sistem antrian, ukuran (besarnya) populasi masukan adalah tak berhingga (Siagian, 1987).
2.4 Uji Distribusi
Perlakuan terhadap input data yang bersifat acak untuk program simulasi dapat dilakukan sebagai berikut (Conover, 1971)
1. Nilai-nilai data tersebut digunakan secara langsung dalam simulasi. Sebagai contoh, jika data menggambarkan waktu pelayanan, maka salah satu data digunakan jika sebuah waktu pelayanan diperlukan dalam sebuah simulasi. Hal ini disebut trace-driven simulation.
2. Nilai data-data tersebut digunakan untuk mendefinisikan sebuah fungsi distribusi umum dengan cara tertentu. Jika diperlukan dalam sebuah simulasi, sampel diambil dari distribusi ini.
3. Data dicocokkan terhadap bentuk teoritis distribusi tertentu, misal eksponensial atau poisson, dengan menampilkan hipotesis tes untuk menentukan kecocokan tersebut (the goodness of fit). Pencocokan ini menghasilakan sejumlah parameter statistika. Saat dilakukan simulasi, sampel diambil dari jenis distribusi teoritis dan nilai-nilai parameter yang cocok.
2.5 Notasi Antrian
Notasi yang digunakan adalah sebagai berikut :
n = Jumlah nasabah yang mengantri pada waktu t. k = Jumlah satuan pelayanan
= Tingkat pelayanan = Tingkat kesibukan sistem
o
P = Peluang semua teller menganggur atau tidak ada nasabah dalam sistem
q
L = Peluang panjang antrian s
L = Peluang panjang sistem
q
W = Peluang waktu menunggu dalam antrian
s
W = Peluang waktu menunggu dalam sistem
2.6 Simulasi
Simulasi ialah suatu metodologi untuk melaksanakan percobaan dengan menggunakan model dari satu sistem nyata (Siagian, 1987). Menurut Hasan (2002), simulasi merupakan suatu model pengambilan keputusan dengan mencontoh atau mempergunakan gambaran sebenarnya dari suatu sistem kehidupan dunia nyata tanpa harus mengalaminya pada keadaan yang sesungguhnya.
Simulasi adalah suatu teknik yang dapat digunakan untuk memformulasikan dan memecahkan model – model dari golongan yang luas.
Golongan atau kelas ini sangat luasnya sehingga dapat dikatakan , “ Jika semua cara yang lain gagal, cobalah simulasi”. Keterbatasan metode analitik dalam mengatasi sistem dinamis yang kompleks membuat simulasi sebagai alternatif yang baik.
Model analitik sangat berguna bagi kehidupan sehari-hari, akan tetapi terdapat beberapa keterbatasan antara lain, yaitu :
Misalnya, penyelesaian persoalan program linier dengan masa perencanaan satu tahun, tidak menggambarkan prosedur operasional untuk masa bulan demi bulan, minggu demi minggu, atau hari demi hari. b. Model matematika yang konvensional sering tidak mampu menyajikan
sistem nyata yang lebih besar dan rumit. Sehingga sukar untuk membangun model analitik untuk sistem nyata yang demikian.
c. Model analitik terbatas pemakaiannya dalam hal–hal yang tidak pasti dan aspek dinamis (faktor waktu) dari persoalan manajemen.
Berdasarkan hal di atas, maka konsep simulasi dan penggunaan model simulasi merupakan solusi terhadap ketidakmampuan dari model analitik.
Beberapa kelebihan simulasi adalah sebagai berikut :
a) Simulasi dapat memberi solusi bila model analitik gagal melakukannya. b) Model simulasi lebih realistis terhadap sistem nyata karena memerlukan
asumsi yang lebih sedikit. Misalnya, tenggang waktu dalam model persediaan tidak perlu harus deterministik.
c) Perubahan konfigurasi dan struktur dapat dilaksanakan lebih mudah. Misalnya, banyak aturan dapat dicoba untuk mengubah jumlah langganan dalam sistem antrian.
d) Dalam banyak hal, simulasi lebih murah dari percobaannya sendiri. e) Simulasi dapat digunakan untuk maksud pendidikan.
f) Untuk sejumlah proses dimensi, simulasi memberikan penyelidikan yang langsung dan terperinci dalam periode waktu khusus.
1) Simulasi bukanlah presisi dan juga bukan suatu proses optimisasi. Simulasi tidak menghasilkan solusi, tetapi ia menghasilkan cara untuk menilai solusi termasuk solusi optimal.
2) Model simulasi yang baik dan efektif sangat mahal dan membutuhkan waktu yang lama dibandingkan dengan model analitik.
3) Tidak semua situasi dapat dinilai melalui simulasi kecuali situasi yang memuat ketidakpastian.
2.6.1 Model – Model Simulasi
Model-model simulasi dapat diklasifikasikan dengan beberapa cara. Salah satu pengelompokannya adalah :
a. Model simulasi statis adalah representasi sistem pada waktu-waktu tertentu atau model yang digunakan untuk mempresentasikan sistem dimana waktu tidak mempunyai peranan. Contohnya simulasi perilaku sistem fisika dan matematika.
b. Model simulasi dinamis adalah representasi sistem sepanjang pergantian waktu ke waktu. Contohnya sistem conveyor di pabrik .
c. Model simulasi deterministik adalah model simulasi yang tidak mengandung komponen yang sifatnya probabilistik (random) dan output telah dapat ditentukan ketika sejumlah input dalam hubungan tertentu dimasukkan.
d. Model simulasi stokastik adalah model simulasi yang mengandung input-input probabilistik (random) dan output yang dihasilkan pun sifatnya random.
f. Model simulasi diskrit adalah model suatu sistem dimana perubahan state terjadi pada satuan-satuan waktu yang diskrit sebagai hasil suatu kejadian (event) tertentu (discrete change state variables). Contohnya simulasi pergudangan.
2.6.2 Simulasi Monte Carlo
Metode Monte Carlo adalah algoritma komputasi untuk mensimulasikan berbagai perilaku sistem fisika dan matematika. Metode Monte Carlo digunakan dengan istilah sampling statistik. Penggunaan nama Monte Carlo, yang dipopulerkan oleh para pioner bidang tersebut (termasuk Stanislaw Marcin Ulam, Enrico Fermi, John von Neumann dan Nicholas Metropolis), merupakan nama kasino terkemuka di Monako. Penggunaan keacakan dan sifat pengulangan proses mirip dengan aktivitas yang dilakukan pada sebuah kasino. Dalam autobiografinya Adventures of a Mathematician, Stanislaw Marcin Ulam menyatakan bahwa metode tersebut dinamakan untuk menghormati pamannya yang seorang penjudi, atas saran Metropolis.
Penggunaan metode Monte Carlo memerlukan sejumlah besar bilangan acak, dan hal tersebut semakin mudah dengan perkembangan pembangkit bilangan acak, yang jauh lebih cepat dan praktis dibandingkan dengan metode sebelumnya yang menggunakan tabel bilangan acak untuk sampling statistik.
Jika suatu sistem mengandung elemen yang mengandung faktor kemungkinan, model yang digunakan adalah model Monte Carlo. Dasar dari simulasi Monte Carlo adalah percobaan elemen kemungkinan dengan menggunakan sampel acak (random) untuk sampel yang berdistribusi normal, pembangkit bilangan acak menggunakan rumus distribusi normal. Sedangkan sampel yang tidak berdistribusi normal dibangkitkan dengan 5 tahapan yaitu:
1. Membuat distribusi kemungkinan untuk variabel penting
Gagasan dasar dari simulasi monte carlo adalah membuat nilai dari tiap variabel yang merupakan bagian dari model yang dipelajari. Banyak variabel di dunia nyata yang secara alami mempunyai berbagai kemungkinan yang mungkin ingin kita simulasikan. Salah satu cara umum untuk membuat distribusi kemungkinan untuk suatu variabel adalah memperhitungkan hasil di masa lalu. Kemungkinan atau frekuensi relative untuk tiap kemungkinan hasil dari tiap variabel ditentukan dengan membagi frekuensi observasi dengan jumlah total observasi.
Contoh: Waktu proses dari suatu stasiun kerja tertentu.
2. Membangun distribusi kemungkinan kumulatif untuk tiap‐tiap variabel di tahap pertama
Konversi dari distribusi kemungkinan biasa, kumulatif dilakukan dengan menjumlahkan tiap angka kemungkinan dengan jumlah sebelumnya. Probabilitas kumulatif ini berguna untuk membantu menempatkan nilai random.
3. Menentukan interval angka random untuk tiap variabel
mewakili tiap kemungkinan hasil. hal tersebut ditujukan pada interval angka random. Penentuan interval didasari oleh kemungkinan kumulatif. 4. Membuat angka random
Untuk membuat angka random kita bisa menggunakan Excel spreadsheets dengan menggunakan perintah =rand(), lanjutkan sampai batas yang diinginkan.
5. Membuat simulasi dari rangkaian percobaan