Pembahasan ekstrem fungsi satu variabel dan dua variabel dengan teorema taylor.

Informasi Dokumen

Penulis:

Sihwanto

Pengajar:

Drs. A. Tutoyo, M. Sc

Sekolah: Universitas Sanata Dharma

Mata Pelajaran: Matematika

Topik: Pembahasan Ekstrem Fungsi Satu Variabel dan Dua Variabel Dengan Teorema Taylor

Tipe: skripsi

Tahun: 2007

Kota: Yogyakarta

Ringkasan Dokumen

I. PENDAHULUAN

Bab ini memberikan gambaran umum mengenai latar belakang, rumusan masalah, pembatasan masalah, manfaat, tujuan, metode, dan sistematika penulisan. Penelitian ini berfokus pada penggunaan Teorema Taylor dalam menentukan nilai ekstrem fungsi satu dan dua variabel. Penjelasan ini penting untuk memahami konteks dan relevansi dari pembahasan yang akan dilakukan.

1.1 Latar Belakang

Dalam banyak bidang seperti teknik dan ekonomi, penting untuk menentukan nilai maksimum dan minimum dari suatu fungsi. Penelitian ini bertujuan untuk memberikan pemahaman yang lebih dalam tentang kondisi yang diperlukan untuk mencapai nilai ekstrem tersebut, yang merupakan dasar dalam analisis fungsi.

1.2 Rumusan Masalah

Rumusan masalah ini mencakup bagaimana Teorema Taylor dapat digunakan untuk menjelaskan pemecahan masalah ekstrem fungsi satu dan dua variabel, serta kondisi-kondisi yang diperlukan untuk mencapai ekstrem tersebut.

1.3 Pembatasan Masalah

Pembatasan masalah dalam penelitian ini hanya mencakup ekstrem fungsi satu dan dua variabel dengan menggunakan Teorema Taylor, sehingga fokus analisis tetap terjaga.

1.4 Manfaat Penulisan

Manfaat yang diharapkan adalah agar pembaca dapat memahami dan menerapkan Teorema Taylor dalam penyelesaian masalah ekstrem fungsi, terutama ketika metode lain tidak dapat digunakan.

1.5 Tujuan Penulisan

Tujuan dari penulisan ini adalah untuk memberikan pemahaman yang jelas tentang syarat-syarat yang harus dipenuhi untuk mencapai maksimum dan minimum fungsi, serta penerapan Teorema Taylor dalam konteks ini.

1.6 Metode Penulisan

Metode penulisan yang digunakan adalah metode pustaka, dengan menelaah berbagai sumber literatur yang relevan untuk mendukung argumen dan analisis dalam penelitian ini.

1.7 Sistematika Penulisan

Sistematika penulisan ini menjelaskan struktur skripsi yang terdiri dari lima bab, mulai dari pendahuluan hingga penutup, yang masing-masing memiliki fokus dan tujuan tersendiri.

II. EKSTREM FUNGSI SATU VARIABEL DAN DUA VARIABEL

Bab ini membahas tentang definisi dan kondisi yang diperlukan untuk menentukan nilai maksimum dan minimum dari fungsi satu dan dua variabel. Pemahaman ini sangat penting untuk aplikasi dalam berbagai bidang ilmu.

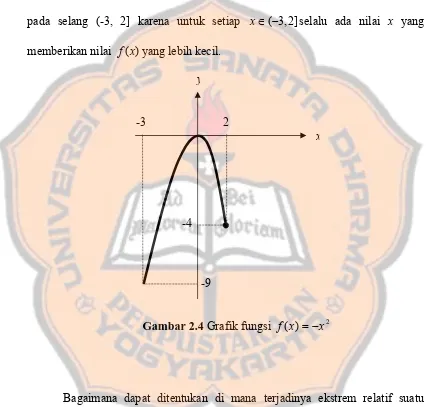
2.1 Maksimum dan Minimum Fungsi dengan Satu Variabel

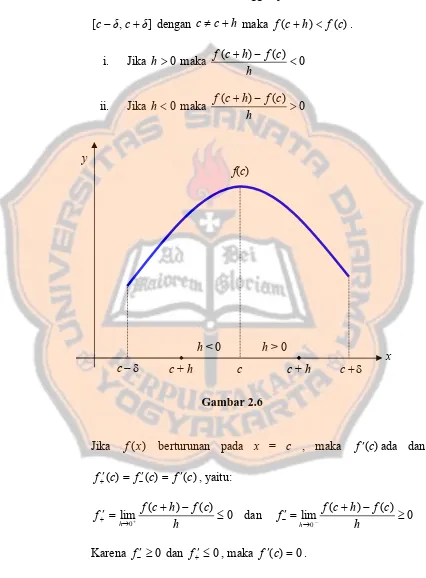
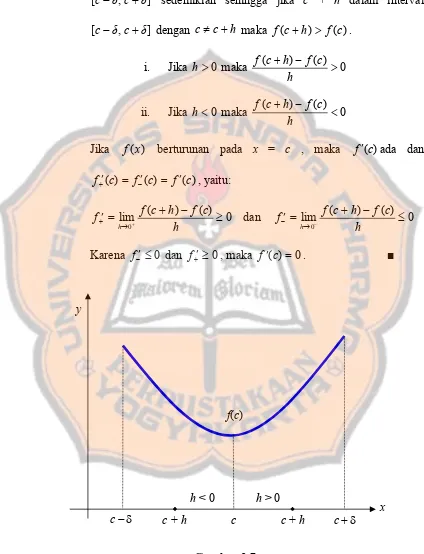
Maksimum dan minimum suatu fungsi satu variabel didefinisikan dengan jelas, termasuk syarat-syarat yang harus dipenuhi untuk mencapai nilai ekstrem. Definisi ini menjadi dasar bagi analisis lebih lanjut dalam konteks fungsi yang lebih kompleks.

2.2 Maksimum dan Minimum Fungsi dengan Dua Variabel

Pembahasan mengenai fungsi dua variabel memperluas konsep ekstrem yang telah dibahas sebelumnya. Dengan menggunakan turunan parsial, kita dapat menentukan titik kritis dan sifat ekstrem dari fungsi tersebut.

III. TEOREMA TAYLOR

Bab ini menjelaskan konsep dasar dari deret pangkat dan Teorema Taylor, yang merupakan alat penting dalam analisis fungsi. Teorema ini memungkinkan kita untuk mendekati fungsi dengan polinomial, sehingga memudahkan dalam menentukan ekstrem.

3.1 Deret Pangkat

Deret pangkat memberikan representasi fungsi dalam bentuk polinomial. Pemahaman ini penting untuk menerapkan Teorema Taylor dalam analisis fungsi.

3.2 Deret Taylor

Deret Taylor adalah ekspansi fungsi di sekitar titik tertentu yang memungkinkan kita untuk menganalisis perilaku fungsi tersebut. Ini adalah langkah awal sebelum menerapkan Teorema Taylor.

3.3 Teorema Taylor untuk Fungsi dengan Satu Variabel

Teorema Taylor untuk fungsi satu variabel memberikan cara untuk menghitung nilai fungsi dan turunannya pada titik tertentu, yang sangat berguna dalam menentukan ekstrem.

3.4 Teorema Taylor untuk Fungsi dengan Dua Variabel

Penerapan Teorema Taylor pada fungsi dua variabel melibatkan penggunaan turunan parsial, yang memungkinkan analisis lebih mendalam mengenai ekstrem fungsi tersebut.

IV. PENGGUNAAN TEOREMA TAYLOR UNTUK MENENTUKAN EKSTREM SUATU FUNGSI

Dalam bab ini, kita akan melihat bagaimana Teorema Taylor diterapkan untuk menentukan ekstrem fungsi. Contoh-contoh konkret akan membantu memperjelas konsep yang telah dibahas sebelumnya.

4.1 Penyelesaian Ekstrem Fungsi untuk Kasus f ′′ ( c ) = 0

Kasus ini menunjukkan bagaimana kita dapat menggunakan Teorema Taylor untuk menganalisis titik kritis ketika turunan kedua sama dengan nol, yang sering kali menjadi tantangan dalam analisis fungsi.

4.2 Penyelesaian Ekstrem Fungsi untuk Kasus H ( a , b ) = 0

Dalam konteks fungsi dua variabel, analisis dilakukan untuk kasus di mana H ( a , b ) sama dengan nol. Ini memberikan wawasan tentang kondisi yang lebih kompleks dalam menentukan ekstrem.

V. PENUTUP

Bab ini menyimpulkan hasil-hasil yang diperoleh dari penelitian ini, serta menggarisbawahi pentingnya pemahaman tentang Teorema Taylor dalam analisis ekstrem fungsi. Penelitian ini diharapkan dapat memberikan kontribusi yang berarti dalam studi lebih lanjut tentang fungsi matematis.