3. Grafik Fungsi Trigonometri.doc

(1)

GRAFIK FUNGSI TRIGONOMETRI GRAFIK FUNGSI TRIGONOMETRI

Langkah – langkah menggambar grafik fungsi trigonometri : Langkah – langkah menggambar grafik fungsi trigonometri : a.

a. MelMelengengkapi kapi tabtabel sel sudut udut – sud– sudut iut iststimeimewa.wa. b.

b. Menentukan titik pada bidang kartesiusMenentukan titik pada bidang kartesius c.

c. MenghuMenghubungkan bungkan titititik – tik – titik tetik tersebursebut sehit sehingga mengga membentmbentuk suatuk suatu kurvau kurva..

1. GRAFIK SINUS 1. GRAFIK SINUS

y

y = sin = sin x x

Tabel : Tabel :

x

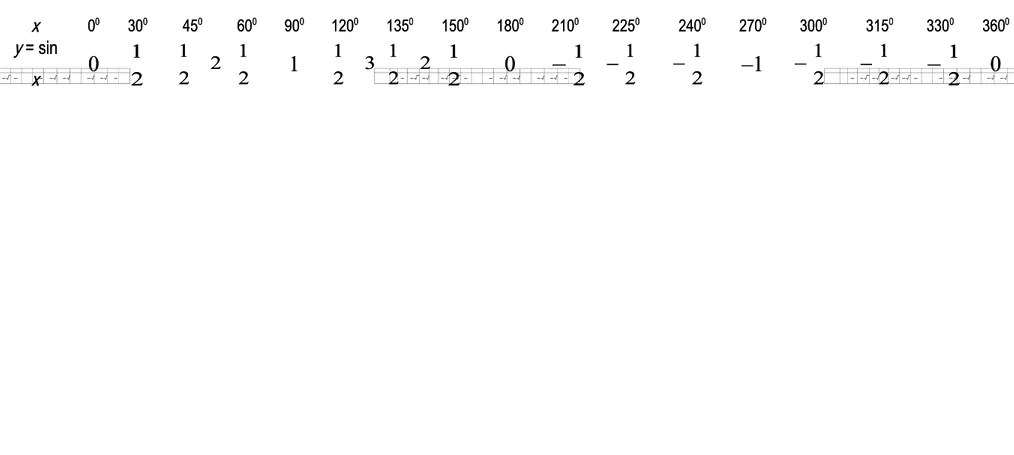
x 0000 303000 454500 606000 909000 12012000 13513500 15015000 18018000 21021000 22522500 24024000 27027000 30030000 31531500 33033000 36036000 y

y = sin = sin x x 00 22 1 1 ₂₂ 2 2 1 1 2 2 1 1 1 1  2 2 1 1 2 2 2 2 1 1 2 2 1 1 0 0 2 2 1 1   2 2 1 1   2 2 1 1   –1 –1 2 2 1 1   ₂₂ 1 1   2 2 1 1   00

!ada gambar "ang diperoleh dapat disimpulkan bahwa grafik sinus adalah : !ada gambar "ang diperoleh dapat disimpulkan bahwa grafik sinus adalah :

!ada gambar diperoleh bahwa : !ada gambar diperoleh bahwa : Nilai maksimum dari fungsi

Nilai maksimum dari fungsi sinsin x x adalah adalah 11 Nilai minimum dari fungsi

Nilai minimum dari fungsi sinsin x x adalah adalah –1 –1

Atau, dapat ditulis

Atau, dapat ditulis : : –1  sin –1  sin x x  1  1

S!"ara Umum# $!n%uk &!rsamaan grafik sinus adalah ' S!"ara Umum# $!n%uk &!rsamaan grafik sinus adalah '

y

= A sin k (

x

)

c

*

#eterangan : #eterangan :

$

$ %% amamplpliittududo o &&mamaksksimimum um ' ' mimininimumum(m(

k k %% T T   2 2 T

T %% perperiodiode & 1 gele & 1 gelombombang "aang "ang teng terdirdiri dari dari 1 bukri 1 bukit dait dan 1 lemn 1 lembah(bah( T

T == %!r%!rdirdiri dai dari + rri + ruas uas ,an,ang sag sama $ma $!s!sarar.. cc %% absabsis is titititik awk awal gal grarafifik) "k) "aiaitu :tu :

x

x - -cc# ar%in,a dig!s!r k!# ar%in,a dig!s!r k! kirikiri s!auh s!auh cc x

x – –cc# ar%in,a dig!s!r k! kanan# ar%in,a dig!s!r k! kanan s!auh s!auh cc

/ / 0/ 0/ // 1/ 1/ / / / / 23/23/// 45/45///

(2)

Contoh :

Tentukan nilai maksimum) minimum) periode dari grafik fungsi trigonometri berikut) kemudian gambarkan grafikn"a :

a. y % sin 2 x e. y % 1 * sin 2 x i. y % 1 – sin &2 x – 00₍

b. y % 2 sin x f. y % 1 – sin 2 x +. y % 1 * sin &2 x * 00₍

c. y % 2 sin 2 x g. y % sin &2 x * 00₍

d. y % – sin 2 x h. y % sin &2 x – 00₍

Penyelesaian : a. y = sin 2 x

diperoleh bahwa :

Nilai maksimum = 1 Nilai minimum = –1

k % 2) maka perioden"a adalah :

/ 1/ 2 2 2  _ k T

Artinya, 1 gelombang akan terbentuk pada saat 1,00_{& 1 bukit dan 1 lembah(}

Grafikn,a adalah '

b. y = 2 sin x

diperoleh bahwa :

/ 45/ 2 1 2 2  _ k T

Artinya, 1 gelombang akan terbentuk pada saat -00_{& 1 bukit dan 1 lembah(}

Grafikn,a ' / 0/ / 1/ / / / 45/ / 23/ / +6 146/ 226/ 416/ / 1/ / 45/ / / 0// 23//

(3)

c. y = 2 sin 2 x

diperoleh bahwa :

/ 1/ 2 2 2 2  _ T

Artinya, 1 gelombang akan terbentuk pada saat 1,00 & 1 bukit dan 1 lembah( Grafikn,a '

d. y = 1 - sin 2 x

diperoleh bahwa :

maksimum pada saat sin 2 x % 1) maka : y % 1 * sin 2 x

y % 1 * 1

y % 2 (Nilai maksimum* Titik maksimumn"a adalah :

sin 2 x % 1 sin 2 x % sin 00 2 x % 00_{* k . -0}0 x % /0 * k . 1,00 x % + x% + 6

Ti%ik maksimumn,a adalah       2 + ) atau      2 + 6 )

minimum pada saat sin 2 x % –1 y % 1 * sin 2 x

y % 1 – 1

y % 0 (Nilai minimum* Titik minimumn"a adalah :

sin 2 x % –1 sin 2 x % –sin 00 sin 2 x % sin &–00₍

2 x % –00_{* k . -0}0 x % –/0 * k . 1,00 x % / +6



%  ₊ x = 146/₌ + 4 x = 416/ = + 3

Ti%ik minimumn,a adalah 

      / + ) atau      / + 4 ) atau       / + 3 ) / / 0// _1// / 45/ / 23/ / +6 146/ 226/ 416/

(4)

k % 2) maka perioden"a adalah : / 1/ 2 2 2 2  _ T

Grafikn,a '

e. y = 1 – sin 2 x

diperoleh bahwa :

maksimum pada saat sin 2 x % –1) maka : y % 1 – sin 2 x

y % 1 – &–1(

sin 2 x % –1

sin 2 x % sin &–00₍

2 x % –00

x % –/0 x %

+



Titik maksimumn"a adalah        2 + )

minimum pada saat sin 2 x % 1 y % 1 – sin 2 x

y % 1 – 1

sin 2 x % 1 sin 2 x % sin 00 2 x % 00 x % /0 x % +

Titik minimumn"a adalah       / + )

/ 1/ 2 2 2 2  _ T

Grafikn,a ' / 0/ 1// / / 146 / +6 / +6  226/ 23// 416/ / 45/ / 0/ / 1/ / / 146 / +6 226/ / 23/ 416/ 45// / +6 

(5)

f. y = sin (2 x - 4//_*

y = sin 2 ( x - 16/*memenuhi bentuk y % $ sin k & x * c( dig!s!r k! kiri s!auh 16/

diperoleh bahwa :

maksimum pada saat sin 2 & x * 10_{( % 1) maka :}

y % sin 2 & x * 10₍

sin 2 & x * 10_{( % 1}

sin 2 & x * 10_{( % sin 0}0

2 & x * 10_{( % 0}0_{* k . -0}0 & x * 10_{( % /}0_{* k . 1,0}0 x % 00_{* k . 1,0}0 k = 0  x %4//₌ 5 k = 1  x %21//₌ 5 3

Titik maksimumn"a adalah       1 5 ) atau      1 5 3 )

minimum pada saat sin 2 & x * 10_{( % –1}

y % sin 2 & x * 10₍

y % –1 (Nilai minimum* Titik minimumn"a adalah :

sin 2 & x * 10_{( % –1}

sin 2 & x * 10_{( % sin &–0}0₍

2 & x * 10_{( % –0}0_{* k . -0}0 & x * 10( % –/0 * k . 1,00 x % –-00_{* k . 1,0}0 k = 0 → x % –5//₌ 4  k = 1 → x %12//₌ 4 2 k = 2 → x %4///₌ 4 6

Titik minimumn"a adalah         1 4 ) _  1 4 ) atau      1 4 6 )

/ 1/ 2 2 2 2  _ T

Grafikn,a ' / 3 atau    2 6 / / 12/ / 4/ / 226/ 21/ 4/// / 5/  / 156 4+6 / 45/ / 1/ / 16 

(6)

g. y = sin (2 x – 4//_*

y = sin 2 ( x – 16/* memenuhi bentuk y % $ sin k & x – c( dig!s!r k! kanan s!auh 16/

diperoleh bahwa :

maksimum pada saat sin 2 & x – 10_{( % 1) maka :}

y % sin 2 & x – 10₍

sin 2 & x – 10_{( % 1}

sin 2 & x – 10_{( % sin 0}0

2 & x – 10_{( % 0}0_{* k . -0}0 & x – 10_{( % /}0_{* k . 1,0}0 x % -00_{* k . 1,0}0 k = 0  x %5//₌ 4 k = 1  x %2+//₌ 4 +

Ti%ik maksimumn,a adalah       1 4 ) atau      1 4 + )

minimum pada saat sin 2 & x – 10_{( % –1}

y % sin 2 & x – 10₍

sin 2 & x – 10_{( % –1}

sin 2 & x – 10_{( % sin &–0}0₍

2 & x – 10_{( % –0}0_{* k . -0}0 & x – 10( % –/0 * k . 1,00 x % –00_{* k . 1,0}0 k = 0 → x % –4//₌ 5  k = 1 → x %16//₌ 5 6 k = 2 → x %44//₌ 5 11

Titik minimumn"a adalah         1 5 ) _  1 5 ) atau      1 5 11 )

/ 1/ 2 2 2 2  _ T

Grafikn,a ' / / 16/ / 5/ / 26/ 2+/ / 44/ / 1 atau    6 /6 / 45/ 1/ / 4/  164// 106/

(7)

2. GRAFIK 7OSINUS y = "8s x Tabel : x 00 300 450 600 900 1200 1350 1500 1800 2100 2250 2400 2700 3000 3150 3300 3600 y = sin x 1 2 1 2 2 1 2 1 0  2 1 2 2 1 2 1 –1 2 1 2 1  2 1  0 2 1 ₂ 2 1 2 1 1

!ada gambar "ang diperoleh dapat disimpulkan bahwa grafik cosinus adalah :

!ada gambar diperoleh bahwa :

Nilai maksimum dari fungsi cos x adalah 1 Nilai minimum dari fungsi cos x adalah –1 Atau, dapat ditulis : –1  cos x  1

ecara 3mum) bentuk persamaan grafik cosinus adalah :

y = A "8s k ( x ) c*

#eterangan :

$ % amplitudo &maksimum ' minimum(

k %

T



2

T % periode & 1 gelombang "ang terdiri dari 1 bukit dan 1 lembah( T = %!rdiri dari + ruas ,ang sama $!sar.

c % absis titik awal grafik) "aitu :

x - c# ar%in,a dig!s!r k! kiri s!auh c x – c# ar%in,a dig!s!r k! kanan s!auh c

/ 0/ / 1/ / / / 23/ 45//

(8)

Contoh :

Tentukan nilai maksimum) minimum) periode dari grafik fungsi trigonometri berikut) kemudian gambarkan grafikn"a :

a. y % cos 2 x e. y % 1 * cos 2 x i. y % 1 – cos &2 x – 00₍

b. y % 2 cos x f. y % 1 – cos 2 x +. y % 1 * cos &2 x * 00₍

c. y % 2 cos 2 x g. y % cos &2 x * 00₍

d. y % – cos 2 x h. y % cos &2 x – 00₍

Penyelesaian : a. y = "8s 2 x

diperoleh bahwa :

4ilai maksimum % 1 4ilai minimum % –1

/ 1/ 2 2 2  _ k T

Grafikn,a adalah '

b. y = 2 "8s x

diperoleh bahwa :

4ilai maksimum % 2 4ilai minimum % –2

/ 45/ 2 1 2 2  _ k T

Artinya, 1 gelombang akan terbentuk pada saat -00_{& 1 bukit dan 1 lembah(}

Grafikn,a ' / 1/ / 45/ / / 0// 23// / 0/ _1// / / +6/ 146/

(9)

c. y = 2 "8s 2 x

diperoleh bahwa :

4ilai maksimum % 2 4ilai minimum % –2 k % 2) maka perioden"a adalah :

/ 1/ 2 2 2 2  _ T

Artinya, 1 gelombang akan terbentuk pada saat 1,00 & 1 bukit dan 1 lembah( Grafikn,a '

d. y = – "8s 2 x

diperoleh bahwa :

maksimum pada saat cos 2 x % –1) maka : y % – cos 2 x

y % – &–1(

cos 2 x % –1

cos 2 x % cos 1,00

2 x % 1,00 * k . -00 x % 00_{* k . 1,0}0

x %0//

Ti%ik maksimumn,a adalah # 1 2

minimum pada saat cos 2 x % 1 y % – cos 2 x

cos 2 x % 1 cos 2 x % cos 1,00 2 x % 1,00_{* k . -0}0 x % 00 _{* k . 1,0}0 x %/0 x %1/0

Ti%ik minimumn,a adalah / # 1 _atau

/ 1/ 2 2 2 2  _ T

Grafikn,a ' e. y = 1 - "8s 2 x / 0/ / 1/ / / / 1 # 2 +6 146/ / 0/ 1// / / 146 / +6

(10)

diperoleh bahwa :

maksimum pada saat cos 2 x % 1) maka : y % 1 * cos 2 x

y % 1 * 1

cos 2 x % 1 cos 2 x % cos 00 2 x % 00_{* k . -0}0 x % 00_{* k . 1,0}0 x %// x%1/0

Ti%ik maksimumn,a adalah / # 2 _atau # 2

minimum pada saat cos 2 x % –1 y % 1 * cos 2 x

y % 1 – 1

cos 2 x % –1 cos 2 x % cos 1,00 2 x % 1,00_{* k . -0}0 x % 00 _{* k . 1,0}0 x %0/0 x %0/0

Ti%ik minimumn,a adalah # / 2

/ 1/ 2 2 2 2  _ T

Artinya, 1 gelombang akan terbentuk pada saat 1,00 & 1 bukit dan 1 lembah( Grafikn,a ' / 0/ 1// / / 146 / +6

(11)

f. y = 1 – "8s 2 x

diperoleh bahwa :

maksimum pada saat cos 2 x % –1) maka : y % 1 – cos 2 x

y % 1 – &–1(

cos 2 x % –1

cos 2 x % cos 1,00

2 x % 1,00_{* k . -0}0

x % 00_{*k . 1,0}0

x % 00

Titik maksimumn"a adalah # 2 2

minimum pada saat cos 2 x % 1 y % 1 – cos 2 x

y % 1 – 1

cos 2 x % 1 cos 2 x % cos 00 2 x % 00_{* k . -0}0 x % 00 * k . 1,00 x %/0 x %1/0

Titik minimumn"a adalah / # / _dan # /

/ 1/ 2 2 2 2  _ T

Grafikn,a '

g. y = "8s (2 x - 4//_*

y = "8s 2 ( x - 16/_* _{memenuhi bentuk y % $ cos k & x * c(}_{dig!s!r k! kiri s!auh 16}/ diperoleh bahwa :

maksimum pada saat cos 2 & x * 10( % 1) maka : y % cos 2 & x * 10₍

cos 2 & x * 10_{( % 1}

cos 2 & x * 10_{( % cos 0}0

2 & x * 10_{( % 0}0_{* k . -0}0

& x * 10_{( % 0}0_{* k . 1,0}0

x % –10 * k . 1,00 k = 0  x % –16/

k = 1  x %146/

Titik maksimumn"a adalah 16/ # 1 _atau 146/ # 1

minimum pada saat cos 2 & x * 10_{( % 0}0

y % cos 2 & x * 10(

y % –1 (Nilai minimum*

/ 0/ / 1/ / / 146 / +6

(12)

Titik minimumn"a adalah : cos 2 & x * 10_{( % –1}

cos 2 & x * 10( % cos 1,00 2 & x * 10_{( % 1,0}0_{* k . -0}0

& x * 10( % 00 * k . 1,00 x % 50_{* k . 1,0}0

k = 0 → x %36/ k = 1 → x %266/

Titik minimumn"a adalah 36/ # 1 _atau 266/ # 1

/ 1/ 2 2 2 2  _ T

Grafikn,a '

h. y = "8s (2 x – 4//_*

y = "8s 2 ( x – 16/_* _{memenuhi bentuk y % $ cos k & x * c(} _{dig!s!r k! kanan s!auh 16}/ diperoleh bahwa :

maksimum pada saat cos 2 & x – 10_{( % 1) maka :}

y % cos 2 & x – 10₍

cos 2 & x – 10_{( % 1}

cos 2 & x – 10_{( % cos 0}0

2 & x – 10_{( % 0}0_{* k . -0}0

& x – 10_{( % 0}0_{* k . 1,0}0

x % 10_{* k . 1,0}0

k = 0  x %16/

k = 1  x %106/

Titik maksimumn"a adalah 16/ # 1 _atau 106/ # 1

minimum pada saat cos 2 & x – 10_{( % –1}

y % cos 2 & x – 10₍

cos 2 & x – 10_{( % –1}

cos 2 & x – 10_{( % cos 1,0}0

2 & x – 10_{( % 1,0}0_{* k . -0}0

& x – 10( % 00 * k . 1,00 x % 100_{* k . 1,0}0

k = 0 → x %1/6/

Titik minimumn"a adalah 36/ # 1 _atau 266/ # 1

/ 1/ 2 2 2 2  _ T 36 / _4/ ₁₅₆_1/ 16 +6 0/12/146

(13)

Grafikn,a '

5/

(14)

4. GRAFIK TANGEN y = %ang!n x Tabel : x 00 300 450 600 900 1200 1350 1500 1800 2100 2250 2400 2700 3000 3150 3300 3600 y = sin x 0 4 4 1 1 4 –1 4 1 0 4 4 1 1 0 4 –1 4 1 1

!ada gambar diperoleh bahwa :

Nilai maksimum dari fungsi tan x adalah Nilai minimum dari fungsi tan x adalah Atau, dapat ditulis :  tan x 