Metode volume hingga untuk menyelesaikan masalah bendungan-bobol.

(1)

&

d

re

w

&

w

s

w

&a

.#

%

w

€

N

s

ry

H

re

€

%ee

Jurnal

Mcrt

Stcrt

Vol.

1 1

No.

1

Hlm.1-74

Jakarta

Januari 2011

ISSN:

1412 - 1220

JURNAL ILMIAH

ISSN:

1412-1220

C[

T

StUt

(2)

lssN 1412-1220

Mil''S

tut

Vol.

11

No.

1

Januari

2A11

Jurnal ltmiah MATIMATIKA,,SIATISTIKA

(

Mo.

Stot

_lditerbitkan_oleh_]irekt*rar_Ris*r_<J*n

ilil

_BINUS_Universiry memfokuskan pada artiket ilmiah berupa hasit peneLiiiarr, pengembangan ilmu datam biclang matematika, statistika, dan aplikasinya. Tujuan pubtikasi _{jurrraI ini}_{adaLah penyebaruiasan}_hJsit_kajian_{dan penetitian}

ui;;;;;r;;;il;ffi

penguasaan, pengembangan, penerapan matematika dan statistika datam bidang teknik, komputer dan industii, serta

aptikasi lainnya.

Pelindung

Penanggung Jawab Ketua Penyunting

Dewan Penyunting

Editor & Setter

Sekretariat

Alamat Sekretariat

Terbit & ISSN

Direktorat Riset dan HKI

Dekan FST Binus University

Drs. Ngarap im Manik, M.Kom.

Prof. Dr. Gerardus Potta, M.App.Sc

Prof. Dr. EdiAbdurachman. MS, M.Sc

Prof. Bahtiar S. Abbas, Ph.D

Dr. Haryono Soeparno, M.Sc Dr. Ashadi Salf m

Drs. lwa Sungkawa, MS

Rojali, S.5i, M.5i

Dra. Endang Ernawati, M.Lib. Prastari Asri Wiweko, 5.S.

Hotit

Angga Ferdiansyah

Anindito, S.Kom., M.Tl

Direktorat Riset dan Hl{t BINUS Uni',,erslty

Kampus,Anggrek, Jl.Kebnn Jeruk l{aya 22 Kebon Jeruk, Jakarta Barat 1 1 530

Tetp. 021 -5360660 ext. 1 190

Fax. 021 -5300244

http:/ /www. binus.edu

e-mait: manik@binus.edui arrindito€rbinr:s.edu Terbit 2 _{(dua) kati datam setahun {Januari & Juti}}

(3)

lssN 1412-1220

MilT'S

t..t

Vol.

11

No.

1

Januari

2011

Jurnal lLmiah MATEMATIKA,.STATISTIKA (

Mot

Srot

_tditerbitkan oteh Direktorat Riset dan htKi BTNUS Universiry

:l]{:lilj:li,tr*.,?:Y:l

l-tlll:1 ?:'yll.hasit, penetitian,,pensembangan irmu

airi*

niJ"rglnatematika, sratistika, dan aplikasinya- Tuiuan pubtikasi jurnat ini aoatarr penyebarlrJasan nJsil kajian dan penetitian

ui;;i,

;Jri;;il;;ffi;

penguasaan, pengembangan, penerapan matematika dan statjstika datam bidang teknik, komputer dan industii, serta

aptikasi iainnya.

DATTAR

I5I

Sabungan H.Hutapea; Alryadi; Ngarap Im Manik

Rancangan _{Modet Simulasi}_{OptimalisasiAntriarr}_Penumpang_{Busway-Transjakarta}

dengan Metoda _{Multichannei eueue}

(5i mulati on Ptanni ng Mode I

of

Busway-Transjakarta _eueui_{ng apdmalizati}_on

wi th lvlulti _{channel Queue lvlethod)....}

Herry Pribawanto Suryawan

Generalized Mixed Fractional Brownian Molion as a Generatized White Norse

Functionat...

10-19

Alexander A 5 Gunawan

Hubungan Deret Eertingkat Berdasar Bitangan fulerian ciengan operator Beda

({,ascade Series relations based an Eulerian Number with Diff erent

operatarl...

_z0-26 Margaretha 0hyver

Penerapan Metode Transformasi Wavetet Kontinu dan Partial Least Squares _{pada Data Gingerol}

(Continue Wavelet Transform and Portial Ledst Squares Nethad Appraach

in

Gingerot

Data)

ZZ-33

Ro'fah Nur Rachmawati

Pendugaan Furrgsi Intensitas Proses Poisson Periodik dengan Tren Fungsi pangkat

Menggunakan Metode Tipe Kernet

(Estimating lntensity Function of a periodic poisson Process with Cubic Function Trend using Kernet. Type lAethod)..

1-9

Sangadji

Pecahan Berlanjut Berhingga

(Finite Continuous Fraction).

Sudi Mungkasi

Metode Volume Hingga untuk Menyelesaikan Masalah Bendunqan-Bobol

(Finite Volume Method to Conclude Collapse Dam).

Nusar Hajarisman

Atgoritma Penduqaan Modet Regresi Kekar melalui Fenrjuga-M

(Estimated Algorithm

af

Robust Regression Martel through Estimator-N)

34-42

43-51

57-62

(4)

METODE VOLUME HINGGA

UNTUK MENYELESAIKAN MASALAH

BENDUN

GAN.BOBOL-Sudi

Nlungkasi

Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma

Mrican, Tromol Pos 29, Yogyakarta 55002

sudi@usd.ac.id

ABSTRACT

A lot

of clonts ctLn be _./btmclin Intlonesicr, y,hiclt is an ogric'tLlfirrol cottntr\:. Dcttn-breok rrtrtt'

re5rrit in a catastrophic collapse aromtcl the clam. L,nclerstctncling the behot'iour of v'ttter if'dntn-break

hoppens is then important.

In

thi,s paper, v,e ,solt,e clam-breok problents using.finite t,olunte. methotls in

the one-clintensionol cctse. The mctthematicol eclrtations colled the shollov,ttuter eqLtttlirttts got'erning the y:ctter _flows_{ond the anctlytical solutietn}

lo

c/um-breuk problent ore pre,\enrccl. Centrttl-upvirul

nrcthod, one oJ'.finite yolrune methocls, is tested to solte clcunJreuli _ltroltlent.

Keywords:.finite yolurne ntethods, clanrbreak problem, shollov'rt'uter ecltrcrlir.tns

ABSTRAK

Terclapat banyak benclungon yang clopat dijuntpui cli Intlonasicr, _{!-otlg ruerupakan}sttcttlt ilegctr(t

ogrttris. BenclLmgan-bobol clopcrt menyebttbkon _{kehuncurail ):tuto}hebat di dueroh sekitur benclungun.

tJleJt lcttrena ittt, pemahaman sifat gerakan air

jika

bencltmgan-bobol terjodi ntenrpctkcrn hal ycutg

penttng. Daleru mok(tlah

ini,

mosolah bendungan-bobol tliselesaikon ntenggunakctn netocle volmne

hinggct tmtuk kestts sattr climensi. Persumctctn ruulemati,s .vang tlisebrrt persantcttrrt

oir

clangkcrl yung

clttpttt ntenjelaskan uliron

air

dan penyelesaian onnlitis tutttLk nutscrlah bendungut-bobol disaiikurt.

Melocle central-ttpw*ind,

yang

merupokan

sqlah

sotu

jenis

nrctocle t'oltune hingga,

diLtji

untuk

rueny e I es uikon mas al q _hb encl un gan -b o b o l.

Ksts kunci: metode t,olunte ltinggu, rnasalsh bendungan-brfiol, per.\utltqot7 uir tlongkcrl

i.i

.lan nrakalah ini pemah diikutsertakan dan menjadi finalis dalam Olimpiade Kar-va Tulis lnovatil2009 yang

r

,:--'riggarakan oleh Perhimpunar.r Pelajar lndonesia di Perancis.

(5)

PENDAHULUAN

Sebagai suatu negara agraris, Indonesia

memiliki

banyak bendungan

untuk

membantu pengairan' Dalam keadaan yang tidak menguntungkan, misalnya gempa bumi, tinggul bendungan bisa saja bobol _{dan menyebabkan kerusakan}_wilayah

di

_{sekitarnya. oleh^sebab}_itu,_p;;ahaman

aliran air

apabila bendungan bobol sangatlah penting. Hal

ini

dapat _{mlmbantu menjawuf uugui*una}_sebaiknya

pembangunan bendungan ditempatkan, sehingga kerugLn dapat dibuat seklcil

-rrrikl,

apabila terjadi

kebobolan bendungan. Masalah bendungan-boLol dengan topografi rata sudah

dite;kan

penyelesaian

analitisnya. _{Penyelesaian masalah}_tersebut_dengan_{topografiTatu}_d,atar_{telah ditemukan sejak}

1g92

oleh Ritter untuk kasus yang sederhana (Ritter, 1892), sedangkan penyelesaian _untuk_rata_miring_telah

dipaparkan oleh chanson (2006). Dalam praktek yang sebJnarnya irampir tidak ada suafu masalah

bendungan-bobol dengan topografi yang rata sempurna. Dengan demikian, suatu metode yang bisa digunakan untuk menyelesaikan masalah ini dengan topografi slembarang sangatlah diperlukan.

Makalah

ini

memaparkan persamaan gelombang air dangkal atau _{cukup disebut persamaan}

Air

Dangkal (PAD) _{serta suatu metode}_{numeris yang}_disebut_Metode_Volume

inrggo

(Mt/H). pAD

adalah suatu persamaan _{matematis yang menjelaskan}_masalah_{aliran air}_termasuk

ma-salah

bendungan-bobol'

MVH

adalah suatu metode numeris yang dapat digunakan untuk menyelesaikan

pAD

dengan sembarang _{topografi. Agar}_{sederhana, pembahasan}_dalamLakalah_ini_terbatas

pada masalah-masalah satu dimensi,yang artinya hanya vektor dengan arah ke kanan/kiri yang _{dimodielkan, sedang arah ke} depan/belakang dan

ke

atas/bawah

tidak

ikut

dimodelkan.

PAD

merupakan suatu model yang

diperoleh berdasarkan perpindahan massa, momentum,

dan

energi,

yang

ketiganya merupakan

kuantitas-kuantitas kekal. Persamaan

ini

_{membentuk suatu sistem hiperbolik}

,orrlirii.

_dan_rnampu

memberikan penyelesaian _{diskontinu meskipun}_keadaan_awalnya_{halus. Terapan}_pAD_cukup

banyak,

meliputi: _{bendungan-bobol, perambatan tsunami,}_{aliran air}_{sungai, dan}

lainlain.

_Untuk

*"rrdrpuiku,

penyelesaian eksak secara analitis sering kali sangatlah sulit. oGh karena itu, metode-metode numeris termasuk MVH telah dikembangkan.

MVH didasarkan pada bentuk integral hukum kekekalan. _{Metode ini}_{memecah-mecah}_domain

menjadi banyak sel dan mengambil nilai pendekatan rata-rata kuantitas dalam setiap sel.

Di

setiap

waktu, nilai-nilai tersebut diperbarui oleh pendekatan/luxpada setiap ujung sel. Keakuratan metode ini sangat bergantung pada _{fungsi flux}_{numeris yang rnemberikan pendekatan}_flux_{yang sesungguhnya}

|e!ai-k mungkin. Tujuan makalah

ini

adalah_untuklenerapkan

MVH

pada penyelesaian

bendungan-bobol' Hukum kekekalan massa dan kekekalan momentum digunakan _{pada^pAb dalam makalah}

ini

unluk memodelkan

profil

air dangkal. Selain itu, metode

cenial-upwiia

yangmerupakan _salah_satu

jenis

MYH

_akan

diuji

_untuk_{menyelesaikan masalah bendungan-bobol. sJtaniutnya,}

penampilan metode numeris ini dianalisis secara kuantitatif dari kesalahan yang dihasilkan.

anllisis

t<uatitatii3uga

dilakukan dengan membandingkan grafik _{oenyelesaian numeris}_dengan_grafik_penyelesaian_analitis.

Fersamaan

Air

Dangkar dan Masarah Bendungan-Bobol

Bab ini terdiri atas _{dua seksi. Seksi pertama menjelaskan notasi-notasi}_{yang digunakan}

dalam persamaan-persamaan _{matematis serta menyatakan bentuk}

PAD.

_{Seksi kedua}

membahas masalah bendungan-bobol.

Persamaan

Air

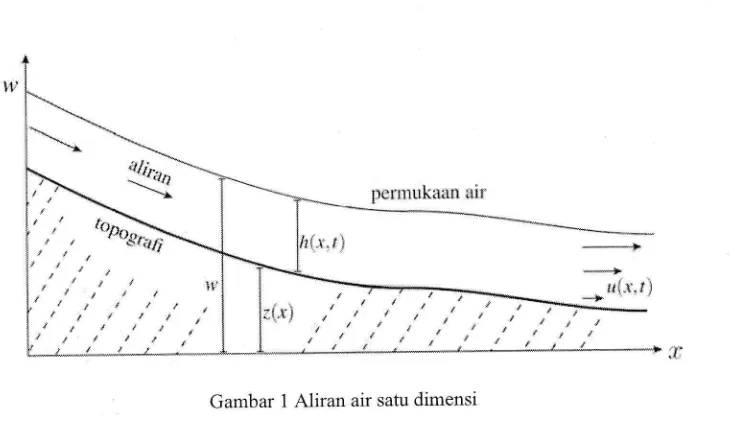
Dangkal

Aliran air _{dangkal dapat digambarkan seperti tampak pada Gambar}_1._{Notasi yang}_digunakan adalah sebagai berikut:

x

mewakili jarak _{yang ditempuh aliran,}

r

_{mewakili variabel}

wakti,

z(x)

adalah topografi

di titik

x,

h(x,t)

adalah ketinggian air di

titik

x

pada _waktu

t,

ty:

z-t

h

_disebfi dengan stage, dan

u(x,/)

mewakili kecepatan aliran di titik x pada _waktu_l.

Mefode Vo/ume Hinggo,,..,, (Sudi Mungkasr)

53

(6)

----perrilukaitn ilil'

f,,IJ ""-**-"*"s

.€

[image:6.612.123.488.73.289.2]

r

Gambar 1 Aliran air satu dimensi

pAD _yang_{juga terkenal}dengan nama sistem Saint-Venant merupakan sistem dua persamaan

simultan yang terairi atas hukurn kekekalan massa dan hukum kekekalan momentum, secara berturut-turut diberikan sebagai berikut

h, +

(ht),

=

O,

I

trr

(htt), +(hu1

+!ght), =-ghz,.

₎

Di

sini,

g

adalah konstanta gravitasi dengan

nilai

9.81 m/s2. Dalam bentuk vektor, PAD (1)

dapat ditulis sebagai q, + _.f(q)

,: s

dengan kuantitas q,

flux

_.f(q) , dan sumber s diberikan oleh

(

-

1,,'

Masalah Bendungan-Bobol

Menyelesaikan masalah bendungan-bobol artinya adalah menentukan aliran yang disebabkan

oleh

bobolnya bendungan secara tiba-tiba. Penyebab bobolnya bendungan

ini

bisa karena usia

bendungan yang sudah tua disertai tidak kuatnya tanggul bendungan menahan air dengan volume yang

terlalu besar, atau bisa saja karena disertai gempa bumi.

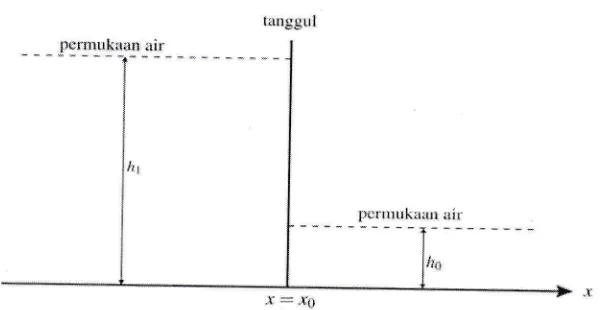
Diasumsikan bahwa suatu bendungan terdiri atas dua bagian dengan ketinggian air yang lebih

rendah pada bagian kanan seperti tampak pada Gambar 2, dan diasumsikan pula bahwa air pada kedua

sisi dalam keadaan diam pada saat awal

(/

=

0).

Secara matematis, kondisi awal

ini

dapat dituliskan

sebagai berikut

(3)

clengan catatan bahwa

h,rho >0.

Pada saat

l=0,

dinding bendungan (tanggul) secara spontan

bobol c1a1 menyebabkan mengalirnya

air

yang lebih tinggi

ke

sisi yang lebih rendah pada waktu berikutnya. Profil aliran dalam rnakalah

ini

terdiri atas ketinggian air, momentum dan kecepatan di trtik.r sembarang dan pada waktu I sembarang.

l'rr^')' '

=[-;,.)

/

ft\

'

=lo,)'

1 @)

rr(

r.o): o

,,.,.0,=

{f;

],ll

i];

Jurna/ltt* St t, Vol, I

I

No.

I

Jonuori 2011: 52-62

(2)

(7)

Gambar 2 Keadaan Awal suafu _{Bendungan dengan Dua Bagian yang Berbeda.}

Penyelesaian analitis masalah tersebut clengan Jn

:0 , ho:0,

dan

hrrO

pertama kali diternukan oleh Ritter (1892). Beberapa _{penulis misalnya Jakeman (2006), Mungkasi (200g)}_dan

Stoker (1957)

jrga

_{membahas penyelesaian}_masalah

analitis

_{bendungan-bofiol,}

yang

mana

penyelesaiannya dapat dituliskan sebagai

dan

(5) Io

,,trl

=

],

[0

ho

0

,..

=r(.'*4*;)

(6)

1,,,

,.r<-rrg/r,

l(r)=

1t,,-:"(,gr,

-l,l

-rrg/r,

<

x<2trglt,

I

[o

'

'r>2ttglr,

,

<

-tnQf

/t

, =

i(,, glt,

-

;l

-trglt,

<.r<2rrglr,

.

x>2rrgi,

untuk setiap waktu

I

>

0.

Lebih lanjut, penyelesaian analitis masalah

di

muka dengan

ro

=

0

dan

hr,

ho >

0

dapat dinyatakan sebagai

h(x)

₌

hl

/_

fr, ₌

*

\l

sh,

-J'

,

x<-tEi

-rr[i[<r'<r(,,-G[)

/

_\

rl,,,-.lsn,)<

r<rS,

-r > /S,

r

<

-/

_rig/r,

-

t

rih,

< -r < r(,,.

-.,s[)

,(,.

-

,Etr)..,.,s,

-r > 15.

(4)

h,=+(,trS-')

u(.t) =

rr, =

s.

-

_;1.

[r*

,

rr

]i'J

(7)

ttrrggLrl

[image:7.612.173.473.75.230.2]

(8)

t > O .

Di

sini kecepatan gelombang shock

S,

bernilai kons

2ghr)

tan dan diberikan oleh

s,

=

2{sh.

*(,

.,,[

#)

-(r

ro,f$

METODE

Metode Volumen Hingga

(MVH)

digunakan untuk menyelesaikan

PAD

secara uumeris' Rumusan pendekatan hukum keiekalan dipergunakan untuk_rnenurunkan skema umum

MVH'

Perlu

diketahui bahwa

MVH

clapat dipergunakan

untuk

menyelesaikan hukum kekekalan

dan

sistem

hiperbolik secara umum. Dipandang

PAD (1)

dengan z

,

--

0.

Suatu

MVH

didasarkan pada

pemecah-mecahan dor-nait-r ruang menjadi banyak sel, dan terus tnenelus lllemantau pendekatan

integral kuantitas cl pada setiap sel tersebut (LeVeque, 2002: 64-65)' Sel ke-l dinotasikan dengan

C,=

(x,-r,z.,xi*ttz)

yang merupakan suatu interval dari

lfr-rrz

hingga

Xi*,2. Nilai

Qi

ne*akili

pendekata, nilai

rata-rata kuantitas r7 pada interval ke-i pada waktu 1,, . yaitu

L

qG,t,)

clx untuk setiap waktu

persamaan

dengan

Ax

=

xi+1t2-

xi-tt2

adalah panjang untuk rata-rata flux di

titik

Jli

=

J;+1/2 _,yaitu

(8)

( 10)

pendekatan (e)

Oi'-L

Ax

sel.

Notasi F,lr,rdigunakan

sebagai

1

Dil -I'.-t _{tltt L}, _t

-Lt

* t

c1(x,t)ctx:

.f'(q@,-,,,,t))'

f

(q@,.,,r,/))

Pengintegralan persamaan (11) terhadap variabel r'vaktu dari t,, hiugga /,,*, menghasilkan

I,rQ,t,,*,)

dx

-

L

q-,t,,) clx=

L

-f(q(*,-,,r,il)dt

-

l'

t(ufxi*r2'D)tu'

l,','.'

f

(q

(*

it1 t 2,

))

dt

(11)

(1 2)

(13)

dengan

Lt

=

t,,n,

-

/,,

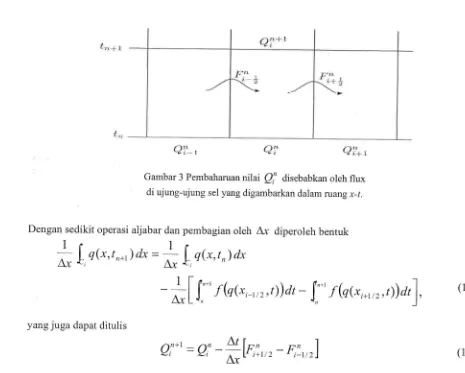
tlerupakan satu langkah waktu'

Karena massa total dalarn sel

ini

berubah hanya bergantung pada

flux di

ujung-ujung sel seperti

tampak pada Gambar 3, kita dapatkan persalnaan

(9)

tp I1

t )t] (

)".

Gambar 3 Pembaharuan nilai

pi'

disebabkan oleh flux

di ujung-ujung _{sel yang digambarkan dalam ruang}_x-t.

Dengan sedikit operasi aljabar dan pembagian oleh

ar

diperoreh bentuk

lrlt

^

I

q(*-t,,-,\dx

=l

Lq$.t,,)dx

Ar

{,

Ar

{,'

*t

!"'

f(,q@,-,'"0)dt-

1,,'.'

.f

G

t*,.r,.,

t!)

cltl,

(14)

( 16)

mempunyai topografi yang topografi yang

tidak

rata

(17) yang juga dapat ditulis

( 1s)

menurut notasi yang diberikan oleh (9) dan (10). Bentuk (14) merupakan bentuk diskrit-penuft; bentuk setengah-diskrit yang berkaitan dengan bentuk ini adalah

)

Lr,+e:

'dt-'

+

F,;,,,,-

Filr,,

=0.

Persamaan (16) rne,ruat asumsi bahwa masalah yang diselesaikan

rata

datar

(2,:0).

Apabila masalah yang drseiesaikan mernpunyai

(z,

*

0 _),maka bentuk setengah-diskrit (16) menjaili

Lr,Le:'

'dt''

+

F,Ir,r-

F,l,,r=

Ar,

s,,

dengan S, adalah diskritisasi sumber.

HASIL

DAN

PEMBAHASAN

Terdapat dua seksi yang akan disajikan,

yaitu: hasil

simulasi bendungan-bobol dengan

topografi rata datar dan hasil simulasi dengan topografi ticlak rata. Secara garis besar, flux-flux dalarn

selrua simulasi dihitung menggunakan ru1-nusan _{central-rtpw,izrl rnenurut Kurganov,}

dkk.

(200

l).

Sebagai _{tambahan, apabila ditemukan suatu topografi}_1,ang_tidak_rata,

yaitu

z.

* 0,

MVH

_yang

_

_ ttjptada

lblumelltnaao*_,

/Sudi Munokosi) ₅₇

{ rtt_'u

[image:9.612.62.527.67.440.2]

(10)

terimbang dengan baik atau biasa disebut well-balanced

finite

volume methods menurut Audusse, dkk. (2004) dan Noelle, dkk. (2006) diterapkan. Semua simulasi dilakukan menggunakan metode berorde dua dengan pembatas lereng minmod;

air

dengan ketinggian

lebih

rendah

dari 10-6

m

tidak dimasukkan dalam perhitungan

flux;

bilangan

CFL=1.0.

Selain

itu,

stage

w=z*h

dan

momentum

p

₌

hu

dianggap kekal. Error dalam perhitungan dikuantifikasi dengan rumus

(18)

dengan i/adalah banyaknya sel, serta

q,

dan

Q,

secara berturut-turut adalah nilai eksak kuantitas dan

nilai pendekatannya untuk sel ke-i. Satuan besaran yang digunakan adalah Sistem Internasional

(S!.

Simulasi Bendungan-Bobol dengan Topografi Rata Datar

Dipandang suatu masalah bendungan-bobol dengan keadaan awal

lJ-E--)

la.-O

IV

a'''

'1

rz(x,O)

:

0

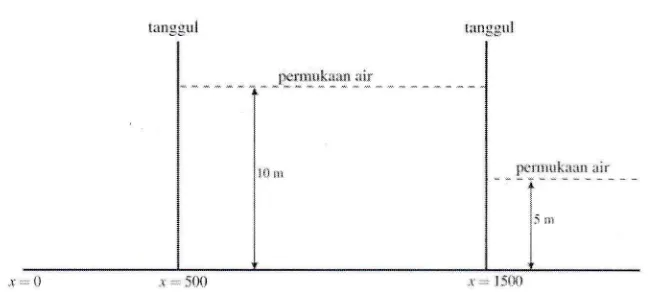
dan ( 1e)

dengan topografi ruta datar seperti tampak pada Gambar 4. Dalam hal

ini,

z =

0

dan h =

w.

Keadaan

awal tersebut menyatakan bahwa terdapat dua tanggul bendungan, yang satu terdapat pada posisi 500

m dan yang satunyapada posisi 1500 m dari acuan. Ada tiga bagian dalam gambar dengan tinggi air berbeda: sisi

kiri

adalah sisi kering, bagian tengah mempunyai ketinggian

air

10

m

dan sisi kanan [image:10.612.135.459.571.720.2]

mempunyai ketinggian air 5 m. Pada saat

t

= 0 _,kedua tanggul bobol. Selanjutnya simulasi dikerjakan untuk memperoleh gambaran gerak air di sembarang titik x dan sembarang waktu l.

Gambar 5 menunjukkan hasil simulasi 20 detik setelah bendungan bobol dengan panjang sel

seragam

Ax:5.

Dalam simulasi

ini

didapatkan error untuk stage, momentum dan kecepatan secara

berturut-turut sebesar 0,028; 0,260; dan 0,606. Nampak pada gambar bahwa ada gelombang yang

bergerak ke

kiri

dan bergerak ke kanan menuju ke arah air yang lebih rendah. Hasil tersebut juga menunjukkan bahwa penyelesaian numeris terjadi penyebaran (difusi\ pada batas afltara wilayah kering dan wilayah basah. Selain

itu,

terjadi pula ketidak-akuratan penyelesaian numeris

di

sekitar

sudut-sudut seperti nampak pada gambar. Hal-hal tersebut merupakan kekurangan metode numeris dalam menyelesaikan masalah.

.r', it I 5{{l .r . litta}

Gambar 4 Keadaan ar'val bendungan topografi rata datar dengan tiga bagian yang berbeda.

Tanggul dan topografi digambar dengan garis tebai. permukaan air dengan uaris putus-putr.rs.

fo

,jika

u(x,o)

=

]to.

,it

u

[s,litu

0<x<500

500<r<1500

1500<-r<2000

lii*r$ui

Jurno/Mut Stat, Vol. I

I

No,

I

Jonuori 2011: 52-62

tar:g.grrl

(11)

{J

0'

PosiFi

Gambar 5 Hasil simulasi setelah 20 detik bendungan bobol topografi rata datar.

Metode menggunakan

Ar

= 5 .

Gambar 6 }.Iasil simuiasi setelah 20 detik bendungan bobol topografi rata datar.

Metode menggunakan

Ar

:

1 .

Namutr deniikian, _{kekurangan-kekurangan tersebut dapat}_diatasi_{dengan menetapkan}_panjalg

sel

At

yang

lebih kecil

_{dengan catatan perhitungan matematis rnenjadi}_lebih_banyak_sehingga simulasi menjadi lebih larna. Sebagai contoh adalah Gambar 6, yang menunjukkal hasil siurulasi

dengan panjang sel seragam

At

= 1 . Error untuk stage, molrentum dan kecepatan dalam simulasi rni

secaraberturut-turutadalahsebesar0,006:0,0571 danO,4gJ.Jelasbahr,vaerroryallgdihasilkandalam simulasi ini jauh lebih kecil drbandingkan hasil simulasi sebelumnya. Tampak pula dalam garnbar

s

G

L 0

ql

*1

4 2

D

P.si5i

* o,

o

Itr

[image:11.612.178.473.72.308.2] [image:11.612.160.468.376.599.2]

(12)

bahwa gelombang yang bergerak

ke

kanan dapat dikontruksi oleh penyelesaian numeris yang

dihasilkan

oleh

MVH

dengan tepat.

Hal

ini

adalah kelebihan

MVH

yang dapat menghasilkan penyelesaian akurat untuk gelombang shock. Keakuratan

ini

disebabkan oleh penurunan

MVH

yang didasarkan pada bentuk integral hukum-hukum kekekalan sebagaimana dijelaskan dalam persamaan

(8)-(15). Pada gambar

ini

juga

tampak bahwa penyebaran penyelesaian numeris masih terjadi di sekitar perbatasan kering dan basah.

Hal ini

bisa terjadi karena

flux

yang diperhitungkan dalam

simulasi adalah hanya flux dari sel-sel yang mempunyai ketinggian air minimum 10-6 m.

Simulasi Bendungan-Bobol dengan Topograli Tidak Rata

Sebagaimana telah dikemukakan dalam Bab PENDAHULUAN, masalah bendungan-bobol dengan topografi rata, sudah ditemukan penyelesaian analitisnya. Akan tetapi,

jika

topografinya tidak

rata, berlekuk-lekuk, atau bahkan diskontinu, masalah bendungan-bobol hanya mungkin dicari

penyelesaiannya menggunakan metode numeris.

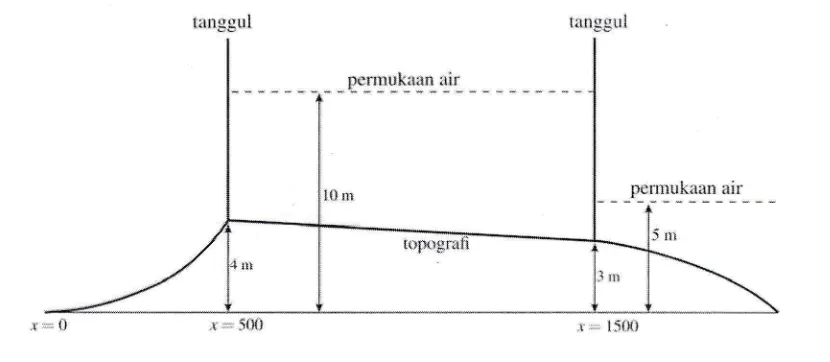
Sebagai contoh masalah bendungan-bobol dengan topografi tidak rata adalah sebagai berikut. Dipandang suatu keadaan awal (19) dengan topografi diberikan oleh

:l[h::::,,,

(20,

2

+3,6.10-2x

-24,jika

1500 < x < 2000. [image:12.612.84.499.432.613.2]

Masalah ini diilustrasikan seperti tampak pada Gambar 7.

Gambar 7 Keadaan awal bendungan topografi tidakrata dengan tiga bagian yang berbeda.

Tanggul dan topografi digambar dengan garis tebal, permukaan air dengan garis putus-putus

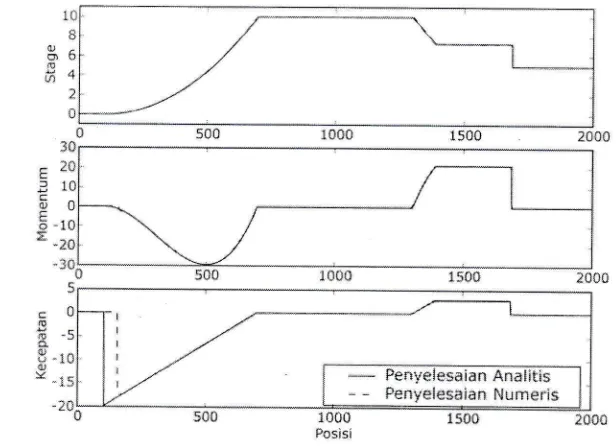
Setelah 20 detik bendungan bobol, hasil sirnulasi gerakan air rnenggunakan

MVII

dapat dilihat pada

Garnbar

8.

Hasil

ini

tentu saja berbeda dengan hasil pada Gambar

5

dan Ganbar

6.

Perbedaan

rrencolok adalah

profil

air

di

sekitar

titik

x

:

500.

Setelah air melalui

titik

x

=

500,

air bergerak

lebih cepat dari pada gerakan pada topografi rata datar.

fr,6

.ro-'r'

z(x):jO,t-10-rx

l-,,,

1o-5x

t;rnggul

I\rl]rr!'lill'l

60 Jurno/ Ma Stut, Vol, I

I

No I

Jonuori 2011: 52-62

(13)

Garnbar 8 Hasil simulasi setelah 20 _{detik be,dungan bobol topografi tidak}_rata.

Metode menggunakan _atr₌_{1. Topografi}_{digambarkan dengan}

titik-titik.

UCAPAN

TERIMA KASIH

Penulis mengucapkan _{terima kasih}_kepada_{Associate Professor}

Stephen _{Roberts (Australian}

National University) atas _{birnbingan yang diberikan.}

PENUTUP

Makalah ini teiah memaparkan _{Metode volume Hingga}_(MVH)

dan terapannya pada masalah

bendungan-bobol' MvH-didasaikan pada bentuk integrai

t-u?r--hrkum

kekekalan _{sehingga cukup} akurat dalam me,yelesaikan _Persamaan_{gelombang ai".}

orrftrl

_(pAD)

yang sering kali melibatkan gelombang _shock'_Keakuratan_ini_{merupa"kan alasan}

utama

-Jrgupu MVH

_adalah_{mltode yang}_cocok

untuk

me.yelesaikan _{rnasalah bendungan-bobo1.}_{nrrg"rr-^iiternukannya}

penyelesaian masaiah

tersebut' gerakan

air

dapat diprediksi

_{sehingga dapa-t rnembantu}

pl."n"ururn

pembangunan bendungan dengan baik' _{Dengan demikian, apabila}_benar-benar_{terjadi bendungan-bobol,}

kerugian yang diakibatkan dapat diminirnalkan.

1

8t

il

*l

l-)

al

E

(ri

r

J

qJ

t

to0*

Posisi

(14)

DAFTAR PUSTAKA

Audusse, E., Bouchut, F., Bristeau, M. O., Klein, R., and Perthame, B. (2004)

A

fast and stable well-balanced scheme with hydrostatic reconstruction fbr shallow water flows, SIAM Journol o.f

Scientific Computing. 25 (6): 2050-2065.

Chanson,

H.

(2006) Analytical solutions of laminar and turbulent darn break wave,

Riler

Flow, hal. 465-474. London: Taylor & Francis Group.

Jakeman, J. (2006) Honottrs Thesis: On lt{umericul Solutions of the Shallow Wuter Wate Ecluations,

tidak diterbitkan. Canberra: The Australian National University.

Kurganov, A., Noelle, S., and Petrova, G. (2001) Sernidiscrete central-upu,ind schemes for hyperbolic conservation laws and hamilton-jacobi equations, SIA]l,I Journol on Scientific Coruputing,23 (3):707-740.

LeVeque,

R.

J.

(2002) Finite-Volume Methods

.for

Hyperbolic Problents. Carnbridge: Cambridge

University Press.

Mungkasi, S. (2008) Mosters Thesis: Finite Volume Methcttl.s.lbr"tlte One-Diruensionol Shallov'lllcter

Eqtrutions, tidak diterbitkan. Canberra: The Australian National University.

Noelle, S., Pankratz, N., Puppo, G., and Natvig, J. R. (2006) Well-balanced flnite

volutle

schemes

of

arbitrary order of accuracy for shallow water flo.,vs, Journol of'Coutlttrtcrtiorutl Plnsics, 213 (2):474-499.

Ritter,

A.

(1892) Die fortpflan^)ng der wasserwellen, Zeitschrift cles Vereine.s Deutscher Ingenieure,

36 (33): 941-9s4.

Stoker, J. J. (1957) Water Waves: The Mathematicol Theory with Applicalion. New York: Interscience Publishers.

Jurnol Ma Stut, Vol, I

I

No,

I

Jonuori 2011: 52-62