matematika diskrit (1) Filsafat Matematika (1) Filsafat Matematika (1)

(1)

Sugi Guritman

Prapto Tri Supriyo

Departemen Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

BOGOR

2004

(2)

Chapter 1 Prinsip Dasar Mencacah

Enumerasi ataupencacahanmerupakan bahasan awal dari matematika diskret yang digunakan sebagai alat dasar untuk mempelajari materi-materi lainnya yang umumnya bersifat kombinatorik. Disamping itu ia juga mempunyai ap-likasi di banyak area seperti: teori peluang, statistika, teori graf, teori koding, kriptogra… dan analisis algoritme. Materi1 _{pembahasannya akan ditekankan} pada:

Aturan Jumlah dan Kali,

Permutasi,

Kombinasi, dan

Kombinasi dengan Pengulangan.

1.1 Aturan Jumlah dan Kali

De…nisi 1.1 (Aturan Jumlah) Jika tugas jenis pertama dapat dilakukan dengan m cara, tugas jenis kedua dapat dilakukan dengan n cara, dan kedua jenis tugas itu tidak dapat dilakukan secara simultan, maka banyaknya cara untuk menyelesaikan tugas-tugas tersebut adalah m+n cara.

Contoh 1.1 Di dalam suatu laboratorium komputer ada 4 printer (merk) jenis laserjet dan6printer jenis deskjet. Jika seorang praktikan diperbolehkan menggunakan kedua jenis printer tersebut, maka ada 4 + 6 = 10printer yang bisa dipilih untuk dipakai.

1_{Beberapa bahasan disampaikan hanya sebagai} _review _{karena telah diberikan pada} matakuliah Matematika Dasar (MAT 212).

(5)

Contoh 1.2 Aturan jumlah dapat diperluas untuk lebih dari dua tugas. Mis-alnya, seorang instruktur laboratorium komputer memiliki4jenis buku bahasa pemrograman: 5 buku (judul) tentang C++, 4 buku tentang FORTRAN, 3

buku tentang Java, dan 5 buku tentang Pascal: Jika seorang praktikan dian-jurkan untuk meminjam satu buku bahasa pemrograman dari sang instruktur, maka ada 5 + 4 + 3 + 5 = 17 buku yang bisa dia pinjam.

De…nisi 1.2 (Aturan Kali) Jika suatu prosedur dapat dipecah menjadi dua tahap, dan jika tahap pertama menghasilkan m keluaran yang mungkin dan masing-masing keluaran dilanjutkan ke tahap kedua dengan n keluaran yang mungkin, maka prosedur tersebut akan menghasilkan mnkeluaran yang mungkin.

Contoh 1.3 Pada Contoh 1.2, jika seorang praktikan diwajibkan menguasai keempat jenis bahasa pemrograman yang masing-masing diberi waktu satu bulan untuk mempelajarinya, maka ada 5 4 3 5 = 120cara belajar yang mungkin.

Dengan aturan kali, de…nisi berikut dengan mudah dapat dipahami.

De…nisi 1.3 Jika dalam suatu kotak berisi n obyek (benda) yang berbeda, maka banyaknya cara memilih (mengambil) r obyek dari kotak itu dengan

urutan diperhatikan dan pengulangan (pengembalian) dibolehkan adalah

nr

Ungkapan dari de…nisi di atas bisa diganti dengan: “banyaknya cara men-empatkannobyek yang berbeda ke dalamrposisi yang berbeda pula dengan pengulangan dibolehkan adalah nr _cara”.

Contoh 1.4 Untuk penyimpanan data, suatu memori utama komputer me-muat sejumlah besar sirkuit, masing-masing mampu menyimpan suatu bit (0

atau 1). Sirkuit simpanan ini disusun berdasarkan satuan-satuan yang dise-but dengansel. Untuk mengidenti…kasi sel di dalam memori utama, masing-masing diberikan satu dan hanya satu nama yang disebut dengan adres. Pada beberapa jenis mesin komputer, adres direpresentasikan sebagai daftar terurut terdiri atas 8 bit yang secara kolektif disebut dengan byte. Dengan aturan kali, maka ada 28 _{adres yang bisa digunakan untuk mengidenti…kasi}

sel dimana informasi akan disimpan.

(6)

1.1 Aturan Jumlah dan Kali 3

Soal 1.1.1 Seorang turis asing akan melakukan perjalanan dari Jakarta ke Bandung menggunakan mobil. Pemandu Wisata menjelaskan bahwa ada2 al-ternatif yang bisa dipilih, yaitu lewat Purwakarta atau Cianjur. Jika memilih jalur Cianjur, ada2alternatif yang bisa dipilih, yaitu lewat Jonggol atau Bo-gor. Jika memilih jalur Bogor, ada 3 alternatif yang bisa dipilih, yaitu lewat Parung, Cibinong, atau Tol, kemudian dari Bogor dilanjutkan dengan 2 al-ternatif, yaitu lewat Puncak atau Sukabumi. Ada berapa cara perjalanan yang bisa ditempuh turis tersebut dari Jakarta ke Bandung, apabila:

1. tanpa batasan apapun.

2. Turis tidak memilih jalur Purwakarta karena tujuannya melancong.

3. Turis ingin mengujungi Kebun Raya Bogor.

4. Turis tidak memilih jalur Puncak karena sering terjadi kemacetan.

Soal 1.1.2 Aminah mempunyai 20 buku yang berberda akan ditempakan di

3 rak berbeda. Tentukan banyaknya cara penempatan jika:

1. tidak ada batasan apapun.

2. tidak ada rak yang kosong.

Soal 1.1.3 Syarat penulisan plat nomor mobil untuk wilayah Bogor dan sek-itarnya adalah:

a. dijit petama harus huruf F,

b. dijit terakhir harus dipilih dari huruf A, B, D, atau E;

c. dijit kedua harus angka yang bukan 0;

d. dijit sisanya harus angka (bebas), dan maksimum ada 3 dijit.

(7)

1.2 Permutasi

Diberikan suatu himpunan yang beranggota n obyek, sembarang susunan linear (mendatar) dari obyek-obyek tersebut disebut permutasi. Permutasi berukuran r dari n obyek bisa diartikan sebagai menempatkann obyek yang berbeda ke dalamrposisi yang berbeda pula dengan cara pengulangan tidak dibolehkan. Jika n obyek dinotasikan dengan a1; a2; :::; an; dan r adalah

intejer positif dengan 1 r n; maka banyaknya permutasi berukuran r

dari n obyek, dinotasikanP(n; r); adalah

n (n 1) (n 2) ::: (n r+ 1) = n!

(n r)!

pos-1 pos-2 pos-3 pos-r

Jelas bahwa P(n; n) = n! dan P(n;1) =n: Berikut ini adalah pende…nisian permutasi dengan ungkapan yang lain.

De…nisi 1.4 Permutasi berukuran r dari n obyek dapat diartikan sebagai seleksi (pengambilan) sebanyak r dari kumpulan yang beranggota n obyek dengan urutan diperhatikan dan pengulangan (pengembalian) tidak di-bolehkan.

Contoh 1.5 Di dalam suatu kelas yang terdiri 10 mahasiswa, dipilih 5 dan disuruh berjajar dalam suatu baris untuk difoto. Tentukan banyaknya susunan yang mungkin.

Jawab. Banyaknya susunan yang mungkin adalah langsung mengikuti kaidah banyaknya permutasi, yaitu P(10;5) = 10 9 8 7 6: z

Contoh 1.6 Susunan huruf (kata) akan dibentuk dengan mengambil huruf-huruf yang ada di dalam kata KOMPUTER. Tentukan banyaknya kata (susun-an huruf tidak harus mempunyai arti) y(susun-ang bisa dibentuk:

1. jika yang diambil semua huruf.

2. jika yang diambil hanya 5 huruf.

3. jika kata terdiri atas 12 huruf dengan syarat pengulangan huruf di-bolehkan.

Jawab. Banyaknya kata yang bisa dibentuk:

(8)

1.2 Permutasi 5

2. jika yang diambil hanya5 huruf adalahP(8;5) = 8! (8 5)!:

3. jika kata terdiri atas 12 huruf dengan syarat pengulangan huruf di-bolehkan adalah 812_:

z

Teorema 1.1 Diberikann obyek, n1 diantaranya berjenis sama (tidak dapat

dibedakan) dan disebut jenis pertama; n2 berjenis kedua; :::; dan nr berjenis

ke r dengan

n1+n2+:::+nr =n;

maka banyaknya susunan berukuran n dari n obyek tersebut adalah

n!

n1! n2! ::: nr!

:

Bukti. Misalkan K adalah banyaknya semua susunan yang dimaksud oleh teorema. Ambil sembarang satu susunan diantara K susunan tersebut, jika semua anggota dari susunan ini dianggap berbeda, maka satu susunan tersebut akan menghasilkann1! n2! ::: nr!susunan yang berbeda. Dengan

demikian, K(n1! n2! ::: nr!) = n! atau

K = n!

n1! n2! ::: nr!

:

z

Contoh 1.7 Tentukan banyaknya kata yang mungkin dibentuk dengan meng-ambil semua huruf di dalam kata MATEMATIKA.

Jawab. Berdasarkan Teorema 1.1, banyaknya kata yang mungkin diben-tuk dengan mengambil semua huruf di dalam kata MATEMATIKA (2M;3A;

2T; 1E; 1I; dan 1K) adalah 10!

(2!)(3!)(2!)(1!)(1!)(1!): z

Contoh 1.8 Buktikan bahwa jika n dank adalah intejer positif dengan n= 2k; maka n!

2k adalah intejer.

Bukti. 2_n_{= 2}_k _{diartikan sebagai kumpulan} _n _{obyek yang mempunyai}_k jenis dengan masing-masing jenis beranggota2obyek yang sama. Banyaknya permutasi berukuranndarinobyek tersebut adalah n!

(2!)k =

(9)

Contoh 1.9 Jika 6 orang didudukkan mengelilingi meja melingkar, maka banyaknya susunan melingkar yang mungkin adalah

5 4 3 2 1 = 5!

Secara umum, jelaskan bahwa banyaknya susunan melingkar berukuran n

adalah

n!

n = (n 1)!:

Jawab. Setiap satu susunan melingkar menghasilkan n susunan linear (mendatar). Jika banyaknya semua susunan melingkar adalanK;makanK =

n! _,

K = n!

n = (n 1)!:

z

Contoh 1.10 5pasang suami-istri didudukkan mengelilingi meja melingkar. Jika duduknya disyaratkan selang-seling laki-laki dan perempuan, tentukan banyaknya susunan yang mungkin.

Jawab. Format susunan melingkar dapat dipandang sebagai format susunan linear dengan membuat satu posisi tetap yang bebas dari pemil-ihan obyek, sedangkan posisi-posisi lainnya mengikuti pola susunan linear. Dalam kasus di contoh ini, ambil satu posisi tetap untuk satu orang dari 5 pasang suami istri tersebut. Selanjutnya, 9 posisi lainnya mengikuti pola susunan linear selang-seling, sehingga diperoleh rumusan

5 4 4 3 3 2 2 1 1 = (5!)(4!):

z

Soal 1.2.1 Daftarkan semua permutasi untuk huruf x; y; z; w:

Soal 1.2.2 Tentukan jumlah permutasi untuk 7 huruf a; b; c; d; x; y; z. Ke-mudian, tentukan jumlah permutasi yang diawali huruf d: Tentukan jumlah permutasi yang diawali huruf d dan diakhiri huruf x atau z:

(10)

1.3 Kombinasi 7

Soal 1.2.4 Dalam bahasa pemrograman “Celebes”, identi…er dituliskan den-gan satu huruf yang diikuti oleh 7 simbol yang berupa huruf atau angka. (Diasumsikan komputer tidak mampu membedakan huruf besar dan kecil, jadi jumlah huruf ada 26). Seperti layaknya bahasa pemrogrman yang lain, Celebes mempunyai “keyword” yang tidak bisa digunakan sebagai identi…er. Jika ada 36 keyword di dalam Celebes, ada berapa identi…er bisa dituliskan?

Soal 1.2.5 Ada berapa susunan dari huruf-huruf di dalam kata SOCIOLOG-ICAL? Kemudian, ada berapa susunan agar A dan G bersebelahan? Ada berapa susunan agar semua vokal bersebelahan?

Soal 1.2.6 Ada berapa intejer positif n yang bisa dibentuk dengan menggu-nakan angka 3; 4; 4; 5; 5; 6; dan 7 sehingga n 5000000:

Soal 1.2.7 Tunjukkan bahwa untuk setiap intejer n; r 0; jika n+ 1 > r;

maka

P(n+ 1; r) = n+ 1

n+ 1 r P(n; r):

Soal 1.2.8 Tentukan nilai n sehingga:

1. P(n;2) = 90:

2. P(n;3) = 3P(n;2):

3. 2P(n;2) + 50 =P(2n;2):

Soal 1.2.9 Ada berapa cara jika 7 orang duduk mengelilingi meja bundar? Kemudian, jika 2 orang ingin duduk bersebelahan, ada berapa susunan yang mungkin?

1.3 Kombinasi

De…nisi 1.5 Kombinasi berukuran r dari n obyek dapat diartikan sebagai seleksi (pengambilan) berukuran r dari kumpulan beranggota n obyek den-gan urutan tidak diperhatikan dan pengulangan (pengembalian) tidak dibolehkan.

(11)

berbeda. Banyaknyakombinasi berukuran r dari n obyek,dinotasikan den-ganC(n; r) atau n_r dan dibaca ”n memilih r”, adalah

C(n; r) = n! (n r)!r! =

P(n; r)

r! :

Rumus ini dijelaskan dengan argumen berikut. Setiapsatu kombinasi beruku-ran r dari n obyek akan menentukanr! permutasi berukuran r dari n obyek, sehingga untuk C(n; r)kombinasi akan menghasikan

C(n; r) (r!) =P(n; r)

Dengan mudah dimengerti bahwa, untuk sembarang intejer positif n,

n

0 = 1,

n

1 =n, dan

n

n = 1:

Selanjutnya, dide…nisikan bahwa n_r = 0 jika:

n tak-positif denganr semua intejer, atau

n positif denganr negatif atau r > n.

Contoh 1.11 Dalam ujian tengah semester Matematika Diskret diberikan

12 soal. Tentukan banyaknya cara mengerjakan soal jika:

1. seorang mahasiswa di wajibkan hanya mengerjakan 8 soal.

2. mahasiswa yang bersangkutan diwajibkan memilih 3 soal dari 5 nomor soal pertama dan memilih 5 soal dari 7 nomor soal terakhir.

3. dari 8 soal yang dikerjakan mahasiswa tersebut, dipilih sedikitnya 3

soal dari 5 nomor soal pertama dan sisanya diambil dari 7 nomor soal terakhir.

Jawab. Perhatikan jawaban-jawaban berikut ini.

1. Banyaknya cara mengerjakan 8soal dari 12soal adalah 12₈ = _4!8!12!:

2. Banyaknya cara mengerjakan 3 soal dari 5 soal pertama adalah 5₃ ;

dan banyaknya cara mengerjakan5soal dari7soal terakhir adalah 7₅ :

(12)

1.3 Kombinasi 9

3. Mengerjakan sedikitnya 3 soal dari 5 nomor soal pertama dan sisanya diambil dari 7 nomor soal terakhir mempunyai tiga alternatif penger-jaan:

(a) 3 soal dari 5 nomor soal pertama dan 5 soal dari 7 nomor soal terakhir, berarti ada 5₃ 7₅ cara pengerjaan.

(b) 4 soal dari 5 nomor soal pertama dan 4 soal dari 7 nomor soal terakhir, berarti ada 5₄ 7₄ cara pengerjaan.

(c) 5 soal dari 5 nomor soal pertama dan 3 soal dari 7 nomor soal terakhir, berarti ada 5₅ 7₃ cara pengerjaan.

Selanjutnya, secara keseluruhan mengikuti aturan jumlah, berarti ada

5

Contoh 1.12 Banyaknya susunan huruf di dalam kata ANTABRANTA ada-lah

10! 4!2!2!1!1!

: 37 800Jika disyaratkan tidak ada dua hurufAyang berdampingan, buktikan bahwa banyaknya susunan huruf menjadi

6! 2!2!1!1!

7 4

Bukti. Pertama, dipandang bahwa huruf A tidak ada, maka banyaknya

susunan huruf tanpa A adalah

6! 2!2!1!1! :

Kemudian setiap satu susunan huruf tanpa A tersebut disisipkan4 huruf A

dengan gambaran sebagai berikut

N T T R N B

(13)

maka banyaknya cara penyisipan mempunyai arti sama dengan banyaknya kombinasi berukuran 4dari 7 obyek, yaitu

7 4 :

Akhirnya dengan aturan kali kita dapatkan jawaban yang dimaksud di atas. z

Contoh 1.13 Di dalam Teori Pengkodean atau Teori Bahasa Komputer, kita mengenal istilahkata(word) ataustringyang dide…nisikan sebagai susu-nan simbol (alfabet). Banyaknya simbol dalam string disebutpanjang string, misalnya diberikan simbol 0,1, dan 2, maka02,22,12, dan 10adalah empat contoh string yang panjangnya 2. Secara umum, jika intejer positif n adalah panjang string, maka banyaknya semua string yang mungkin adalah 3n_;

di-mana 3 adalah banyaknya simbol. Misalkan x=x1x2:::xn adalah salah satu

dari string tersebut,bobot darix, dengan notasi wt(x);dide…nisikan sebagai

wt(x) :=x1+x2+:::+xn:

Ambil contoh: wt(22) = 4; wt(10) = 1;danwt(102) = 3:Dengan pede…nisian ini, maka banyaknya semua string yang panjangnya 10 adalah

310:

Buktikan bahwa banyaknya string yang panjangnya 10 dan berbobot genap adalah

Bukti. Dari de…nisi jelas bahwa suatu string yang panjangnya 10 dan berbobot genap jika dan hanya jika banyaknya simbol 1 dalam string terse-but juga genap. Dengan demikian banyaknya simbol 1 dalam string yang mungkin adalah 0; 2; 4; ..., 10: Misalkan banyaknya simbol 1 dalam string adalah j; maka banyaknya string yang mungkin adalah

10

j 2

(14)

1.3 Kombinasi 11

Bilangan ini diperoleh dari menempatkan simbol 1 sebanyak j ke dalam 10 posisi simbol dalam string:

simbol:

posisi: 1 2 3 5 6 7 8 9 10 :

Banyaknya penempatan yang mungkin adalah 10_j : Selanjutnya, setiap satu penempatan tersebut, (10 j)posisi simbol sisanya ditempati simbol 0atau 2 (urutan diperhatikan dan pengulangan dibolehkan), sehingga banyaknya penempatan yang mungkin adalah 210 j_: _{Kemudian penerapan aturan kali}

menghasilkan 10_j 210 j_{. Akhirnya, untuk semua nilai} _j _{yang mungkin}

diter-apkan aturan jumlah, sehingga diperoleh

Teorema 1.2 (Teorema Binomial)Jikaxdanyadalah variabel dannadalah intejer positif, maka

Ekspansi dari perkalian tersebut menghasilkan jumlahan dengan suku-suku bertipexi_yn i _untuk_i_{= 0}_;₁_;₂_{; :::; n:}_{Banyaknya suku}_xi_yn i _{dalam ekspansi}

tersebut merupakan koe…sien dari xi_yn i_; _yaitu n

i . Bilangan ini diperoleh

dari banyaknya cara memilih i faktor dari n faktor. z

Akibat 1.1 Untuk setiap intejer positif n 1;

1.

(15)

1. x= 1 dan y= 1;

2. x= 1dan y= 1;

z

Contoh 1.14 Himpunan kuasa (power set) dari suatu himpunan A; dino-tasikan dengan _P(A); adalah koleksi (himpunan) semua subhimpunan dari

A: Jika _jA_j=n; dengan n intejer positif, jelaskan bahwa banyaknya subhim-punan berkardinal k; dengan 0 k n; adalah n_k ; dan

jP(A)_j=

Jawab. Menentukan banyaknya subhimpunan berkardinal k dari suatu himpunan berkardinalnmempunyai arti sama dengan menentukan banyaknya pemilihan berukuran k dari n obyek dengan syarat pengulangan tidak di-bolehkan dan urutan tidak diperhatikan. Dengan demikian, banyaknya sub-himpunan berkardinal k;dengan 0 k n; adalah n_k : Selanjutnya, berda-sarkan Akibat 1.1 No. 1, maka

jP(A)_j=

Dengan demikian koe…sien dari x5_y2 _{adalah (yaitu untuk} _i_{= 5)}

7 5 (2

5_{)( 3)}2_:

(16)

1.3 Kombinasi 13

Teorema 1.3 Untuk sembarang intejer n; r dengan n r 1;

n+ 1

Bukti. Walaupun teorema ini bisa dibuktikan secara aljabar, yaitu den-gan menggunakan de…nisi n_r = n!

r!(n r)!; namun disini pembuktian akan di-lakukan secara kombinatorik. Misalkan

A=_fx; a1; a2; :::; ang;

banyaknya subhimpunan berkardinal r dari A adalah n+1_r : Setiap subhim-punan tersebut hanya ada dua kemungkinan: memuat x atau tidak memuat

x: Banyaknya subhimpunan yang memuat x adalah _rn₁ , sedangkan yang tidak memuat x adalah n_r : Dengan aturan jumlah, kita dapatkan rumusan

yang dimaksud. z

Teorema 1.4 (Teorema Multinomial)Untuk intejer positifndant;koe…sien dari

Bukti. Banyaknya sukuxn1

1 xn22xn33:::xn

t

t dalam ekspansi(x1+x2+:::+xt)n

adalah banyaknya cara memilih secara berurutann1 faktor,n2 faktor,:::, dan

nt faktor dari n faktor (x1+x2+:::+xt); yaitu

dan merupakan koe…sien dari sukuxn1

1 xn22xn33:::x

nt

t dalam ekspansi(x1+x2+

(17)

Contoh 1.16 Tentukan koe…sien dari a2_b3_c2_d5 _{dalam ekspansi}

(a+ 2b 3c+ 2d+ 5)16:

Jawab. Karena

(a+ 2b 3c+ 2d+ 5)16= [(a) + (2b) + ( 3c) + (2d) + (5)]16;

dan berdasarkan Teorema Multinomial, maka

16!

(2!)(3!)(2!)(5!)(4!)

adalah koe…sien dari (a)2₍₂_b₎3_{( 3}_c₎2₍₂_d₎5₍₅₎4_: _{Dengan demikian,}

16!

(2!)(3!)(2!)(5!)(4!)(1)

2₍₂₎3_{( 3)}2₍₂₎5₍₅₎4

adalah koe…sien dari a2_b3_c2_d5_: _z

Soal 1.3.1 Hitunglah 6₂ ; dan periksalah jawabannya dengan mendaftarkan semua pemilihan berukuran 2yang bisa dibuat dari huruf a; b; c; x; y;danz:

Soal 1.3.2 Jika n adalah intejer positif dan n > 1; buktikan bahwa n₂ +

n 1

2 merupakan bentuk kuadratik.

Soal 1.3.3 Suatu panitia terdiri dari 12orang yang dipilih dari 10 pria dan

10 wanita. Tentukan banyaknya cara pemilihan, jika:

1. tidak ada batasan apapun.

2. ada 6 pria dan 6 wanita.

3. jumlah wanita harus genap.

4. jumlah wanita harus lebih besar dari pria.

5. ada sedikitnya 8 pria.

Soal 1.3.4 Tentukan banyaknya byte yang memuat banyaknya simbol “1” sedikitnya 5:

(18)

1.3 Kombinasi 15

1. masing-masing anak mendapatkan 3 buku.

2. dua anak yang tertua masing-masing mendapat 4 buku, sedangkan dua yang termuda masing-masing mendapatkan 2 buku.

Soal 1.3.6 Tentukan banyaknya huruf di dalam kata MISSISSIPPI sehingga tidak ada huruf S yang bersebelahan.

Soal 1.3.7 Dari Contoh 1.13, tentukan banyaknya string dengan panjangnya

10 yang:

1. memuat 4 simbol “0”, 3 simbol “1”, dan 3 simbol “2”.

2. memuat sedikitnya 8 simbol “1”.

3. berbobot 4:

Soal 1.3.8 Misalkan string dengan panjang 10 dibentuk dari afabet 0; 1; 2;

dan 3:

1. Tentukan banyaknya string yang berbobot 3:

2. Tentukan banyaknya string yang berbobot genap.

Soal 1.3.9 Tentukan koe…sien dari x9_y3 _{di dalam ekspansi:}

1. (x+y)12_:

2. (x+ 2y)12_:

3. (2x 3y)12_:

Soal 1.3.10 Tentukan koe…sien dari:

1. xyz2 _{di dalam}₍_w₊_x₊_y₊_z₎4_:

2. xyz2 _{di dalam}₍₂_x _y _z₎4_:

3. xyz 2 _{di dalam}₍_x ₂_y_{+ 3}_z 1₎4_:

(19)

Soal 1.3.11 Tentukan jumlah semua koe…sien di dalam ekspansi:

1. (x+y)10_:

2. (x+y+z)10_:

3. (w+x+y+z)5_:

4. (2s 3t+ 5u+ 6v 11w+ 3x+ 2y)10_:

Soal 1.3.12 Untuk sembarang intejer positif n; tentukan:

1.

Soal 1.3.13 Tunjukkan bahwa untuk sembarang intejer positif m dan n ber-laku

n m+n

m = (m+ 1)

m+n m+ 1 :

Soal 1.3.14 Misalkann adalah intejer positif, evaluasi (sederhanakan) jum-lahan

(20)

1.4 Kombinasi dengan pengulangan 17

1.4 Kombinasi dengan pengulangan

De…nisi 1.6 Kombinasi dengan pengulangan berukuran r dari n obyek adalah seleksi (pengambilan) berukuran r dari kumpulan beranggota n obyek dengan urutan tidak diperhatikan dan pengulangan (pengembalian) di-bolehkan.

Teorema 1.5 Banyaknya kombinasi dengan pengulangan berukuran r

dari n obyek adalah

Untuk memperoleh dari mana bilangan dalam teorema tersebut diper-oleh, berikut ini diberikan contoh sebagai ilustrasi untuk menuju ke suatu generalisasi.

Contoh 1.17 Untuk memenuhi syarat kelulusan, 7 orang mahasiwa De-partemen Matematika IPB yang terancam DO (drop out) diwajibkan mengam-bil1mata kuliah pilihan yang dipilih dari4mata kuliah pilihan yang ditawar-kan: Kriptologi, Teori Pengkodean, Matematika Finansial, dan Optimisasi Kombinatorial. Ada berapa cara pemilihan4 mata kuliah oleh ketujuh maha-siswa yang bersangkutan?

Jawab. Misalkan K, T, M, dan O menyatakan Kriptologi, Teori Pengko-dean, Matematika Finansial, dan Optimisasi Kombinatorial. Sebagai gam-baran, suatu contoh cara pemilihan yang mungkin adalah K dipilih oleh 2

mahasiswa, T oleh 2 mahasiswa, M oleh 2 mahasiswa, dan O oleh 1 ma-hasiswa, kemudian dinotasikan dengan K,K,T,T,M,M,O dan ditulis sebagai

xx_jxx_jxx_jx. Agar lebih jelas beberapa cara pemilihan yang mungkin lainnya diberikan dalam tabel berikut ini.

Cara pemilihan yang mungkin Ditulis sebagai K,K,K,K,T,M,O xxxx_jx_jx_jx

(21)

dapat dibawa ke masalah mencari banyaknya permutasi berukuran 10 den-gan2jenis, yaitu7obyek berjenis ”x” dan tiga obyek berjenis ”_j”. Dengan demikian ada

10! 3!7! =

10 7

cara ketujuh mahasiswa tersebut memilih4mata kuliah yang ditawarkan. z Bentuk umum dari Contoh 1.17 adalah banyaknya kombinasi dengan pen-gulangan berukuran r dari n obyek yaitu Persamaan 1.2.

Contoh 1.18 Ada berapa cara apabila13kelereng yang identik didistribusikan ke dalam 5 lubang yang berbeda?

Jawab. Dengan argumen yang sama dengan jawaban Contoh 1.17 diper-oleh jawaban

Contoh 1.19 Tentukan banyaknya semua penyelesaian intejer dari persa-maan

x1+x2+x3+x4 +x5+x6 = 20;

dimana xi 0 untuk setiap 1 i 6:

Jawab. Dengan argumen yang sama dengan jawaban Contoh 1.17 diper-oleh jawaban

Catatan 1.1 Dari ketiga contoh terakhir di atas, kita sampai pada kesim-pulan bahwa ketiga pernyataan berikut adalah ekuivalen:

1. Banyaknya pemilihan berukuran r dari koleksi beranggotan obyek den-gan urutan tidak diperhatikan dan pengulang dibolehkan.

2. Banyaknya solusi intejer dari persamaan

x1+x2+:::+xn =r;

(22)

3. Banyaknya cara pendistribusian apabila r obyek yang identik didis-tribusikan ke dalam n wadah yang berbeda.

Contoh 1.20 Ada berapa cara apabila kita ingin memberikan 7 apel dan 6

jeruk kepada 4 orang anak apabila masing-masing anak sedikitnya menerima

1 apel?

Jawab. Tetapkan dulu bahwa masing-masing anak telah menerima 1 apel, sehingga ada 4+3 1₃ cara pendistribusian 3 apel sisanya. Setiap cara ini kemudian diikuti dengan pendistribusian 6 jeruk yaitu 4+6 1₆ . Dengan aturan kali diperoleh jawab

1 6

3

9 6 :

z

Contoh 1.21 Tentukan banyaknya solusi intejer dari persamaan

x1+x2+x3+x4+x5+x6 <200; (1.3)

dimana xi 0 dengan 1 i 6: Jelaskan problem komputasinya!

Jawab. 3_Misalkan

x1+x2+x3+x4+x5+x6 =k; (1.4)

maka banyaknya solusi yang dimaksud adalah semua solusi Persamaan 1.4, untuk 0 k 199:Dengan aturan jumlah diperoleh jawaban

199 X

k=0

6 +k 1

k :

Jawaban ini kalau dicari nilainya cukup melelahkan; apalagi kalau ruas kanan Pertidaksamaan 1.3 jauh lebih besar dari 200; katakanlah 2000: Berikut ini diberikan penyelesaian dengan pendekatanidentitas kombinatorial. Men-cari banyaknya solusi intejer dari Pertidaksamaan 1.3 setara dengan menMen-cari banyaknya semua solusi persamaan

x1+x2+x3+x4+x5 +x6+x7 = 200;

(23)

dimana xi 0 untuk setiap 1 i 6 dan x7 > 0: Problem ini juga setara dengan problem mencari jumlah solusi intejer untuk

y1+y2 +y3+y4+y5+y6+y7 = 199;

dimana xi = yi untuk setiap 1 i 6 dan y7 = x7 1 (sekarang yi 0

untuk setiap 1 i 7): Dengan demikian solusinya adalah

199 + 7 1

Contoh 1.22 Setiap intejer positif m dapat dinyatakan sebagai jumlahan intejer-intejer positif lainnya yang tidak lebih dari m dengan urutan diper-hatikan. Jumlahan yang demikian disebut komposisi darim: Misalnya, se-mua komposisi dari 4ada 8; yaitu: 4;3 + 1;1 + 3;2 + 2; 2 + 1 + 1; 1 + 2 + 1;

1 + 1 + 2; dan 1 + 1 + 1 + 1: Secara umum, berapa banyaknya komposisi dari

m?

Jawab. Problem menentukan banyaknya semua komposisi darimsetara dengan problem menentukan banyaknya solusi intejer dari persamaan:

x1+x2+:::+xk=m;

dimana xi 1 untuk setiap 1 i k; dan k adalah intejer dengan 1

k m: Dengan mengambil yi = xi 1 untuk setiap 1 i k; kemudian

persamaan itu ditransformasikan menjadi

y1+y2+:::+yk=m k;

dimana yi 0 untuk setiap 1 i k dan 1 k m: Banyaknya solusi

intejer dari persamaan terakhir ini adalah

(24)

z

Contoh 1.23 Perhatikan segmen program berikut, dimanai; j;dank adalah peubah-peubah intejer.

Jawab. Sebagai gambaran, beberapa contoh pilihan i; j; dan k (dalam urutan: i pertama, j kedua, dan k ketiga) adalah: (1;1;1); (2;1;1);

(2;2;1);(3;2;1);(17;12;5);(16;16;2);dan (13;6;6):Catatan bahwa(1;2;1) dan (1;1;2) tidak mungkin; demikian juga (17;5;12); (12;17;5); (12;5;17);

(5;12;17);dan(5;17;12):Gambaran ini membawa kita pada suatu kesimpu-lan bahwa banyaknya kali perintah print dieksekusi setara dengan pemili-han berukuran3dari kumpulan obyek_f1;2; :::;20_gdengan pengurutan tidak diperhatikan dan pengulangan dibolehkan, yaitu

20 + 3 1

3 :

Jawaban ini juga dapat diperoleh dengan cara lain, misalnya menggunakan

diagram pohon. z

Contoh 1.24 Perhatikan segmen program berikut, dimanai; j; n danCO U N T ER adalah peubah-peubah intejer dengan COU N T ER di berikan nilai awal 0:

COU N T ER:= 0

for i:= 1 to n do for j := 1 to i do

COU N T ER:=COU N T ER+ 1

Pertanyaannya, berapa nilai COU N T ER setelah segmen tersebut diek-sekusi?

Jawab. NilaiCOU N T ERtersebut setara dengan banyaknya pemilihan nilai-nilai i dan j yang mungkin, yaitu

n+ 2 1

2 =

n(n+ 1)

2 :

(25)

Ringkasan

Ringkasan bahasan dalam bab ini adalah membandingkan pengertian pemil-ihan berukuran r dari kumpulan beranggotan obyek, yang diberikan dalam tabel berikut.

Urutan (YA) Urutan (TIDAK) Ulangan (YA) nr (n+r 1)!

r!(n 1)!

Ulangan (TIDAK) P(n; r) = ₍_{n r}n!_)! C(n; r) = _r_!(_{n r}n! _)!

Soal 1.4.1 Tentukan ada berapa cara pendistribusian10koin kepada5orang anak jika:

1. tidak ada batasan apapun,

2. setiap anak sedikitnya mendapatkan 1 koin, dan

3. anak yang tertua sedikitnya mendapatkan 2 koin.

Soal 1.4.2 Tentukan banyaknya semua solusi intejer dari persamaan

x1+x2+x3 +x4 = 32;

apabila:

1. xi 0; 1 i 4;

2. xi >0; 1 i 4;

3. x1; x2 5; x3; x4 7;

4. xi 8; 1 i 4;

5. xi 2; 1 i 4; dan

6. x1; x2; x3 >0; 0< x4 25:

Soal 1.4.3 Dua intejer berdijit-n (awalan 0 dibolehkan) disebut ekuivalen

jika yang satu merupakan permutasi dari yang lain. Ilustrasi: 12033; 20331;

dan 01332 adalah contoh tiga intejer berdijit-5 yang saling ekuivalen.

(26)

2. Jika dijit 1; 3; dan 7 harus muncul paling banyak satu kali, tentukan banyaknya semua intejer berdijit-5 yang saling tidak ekuivalen.

Soal 1.4.4 Tentukan jumlah solusi intejer dari persamaan

x1+x2+x3+x4 +x5 <500;

jika:

1. xi 0; 1 i 5:

2. xi 2; 1 i 5:

Soal 1.4.5 Perhatikan segmen program berikut, dimanai; j; k danm adalah peubah-peubah intejer.

for i:= 1 to 20do for j := 1 to i do

for k:= 1 to j do for m := 1 to k do

print (i j) + (k m)

Berapa kali perintah print dieksekusi?

Soal 1.4.6 Perhatikan segmen program berikut, dimana i; j; k dan CO U N T ER adalah peubah-peubah intejer dengan COU N T ER di berikan nilai awal 10:

COU N T ER:= 10

for i:= 1 to 15do for j := 1 to 15 do

for k := 1 to 15 do

COU N T ER:=COU N T ER+ 1

Pertanyaannya, berapa nilai COU N T ER setelah segmen tersebut diek-sekusi?

Soal 1.4.7 Perhatikan segmen program berikut, dimana i; j; k; IN CREA

-M EN T dan SU M adalah peubah-peubah intejer.

IN CREAM EN T := 0

SU M := 0

for i:= 1 to 10do for j := 1 to i do

for k := 1 to j do

IN CREAM EN T :=IN CREAM EN T + 1

SU M :=SU M +IN CREAM EN T

(27)

Soal 1.4.8 Tulislah program komputer (atau, bangunlah suatu algoritme) yang outputnya semua solusi intejer dari:

1. x1+x2+x3 = 10; 0 xi; 1 i 3:

(28)

Chapter 2 Sifat Dasar Intejer

Di dalam bab ini, pembicaraan banyak terkait dengan sifat-sifat dasar inte-jer (bilangan bulat). Materinya ditekankan pada bahasan tentang: induksi matematik, de…nisi rekursif, dan algoritme pembagian.

2.1 Prinsip Induksi Matematik

Topik bahasan intejer tidak terlepas dari notasi himpunan bilangan. Be-berapa notasi himpunan bilangan yang umum dipakai diantaranya: Z meno-tasikan himpunan semua bilangan bulat yang anggotanya disebutintejer,Z+ menotasikan himpunan semua intejer positif, N menotasikan himpunan se-mua intejer tak-negatif,Rmenotasikan himpunan semua bilangan nyata, dan Qmenotasikan himpunan semua bilangan rasional. Secara sama, penotasian R+ _dan _Q+ _{adalah untuk himpunan bilangan nyata dan rasional positif.}

Pada setiap himpunan bilangan di atas dapat dikenai relasi urutan: " = "; " < ", atau "> ". Artinya untuk setiap dua bilangan a dan b; satu dan hanya satu berlaku:

"a=b"; "a < b"; atau "a > b":

Sifat dasar intejer yang melandasi induksi matematik dinyatakan pada prin-sip berikut ini.

Prinsip Pengurutan Baik (well-ordering principle): Setiap subhimpunan tak-kosong dari Z+ _{mempunyai unsur terkecil.}

Teorema 2.1 (Prinsip induksi matematik) MisalkanS(n) menotasikan suatu pernyataan matematik terbuka yang melibatkan peubah intejer positif

n: Jika:

(29)

(a) S(1) benar, dan

(b) untuk sembarang pilihan k₂Z+_; _berlaku: _S₍_k₎₎_S₍_k_{+ 1)}_;

kesimpulannya: S(n) benar untuk semua n₂Z+_:

Bukti. MisalkanS(n)adalah suatu pernyataan terbuka yang memenuhi syarat (a) dan (b), dan misalkanF =_ft₂Z+ _S₍_t₎_salah_g_:_{Akan dibuktikan} bahwaF =?:AndaikanF ₆=?;berdasarkan prinsip pengurutan baik, maka

F mempunyai unsur terkecil s:Karena S(1) benar, maka jelas bahwa s >1;

dan akibatnya s 1₂ Z+_: _Karena _s _{terkecil, maka} ₍_s ₁₎ ₂₌ _F; _{ini berarti}

S(s 1)benar. Dari fakta ini dan berdasarkan syarat (b), maka S(s)harus benar, suatu kontradiksi bahwa s₂F yang berartiS(s)salah. Pengandaian harus diingkar dan kita simpulkan bahwa F =?: z Prinsip induksi matematik disebut juga prinsip induksi berhingga. Di dalam teorema di atas, syarat (a) disebutlangkah basis dan syarat (b) disebut

langkah induktif. Catatan bahwa pada langkah basisS(n)benar tidak harus dimulai untuk n = 1; tetapi secara umum bisa digantikan untuk n = n0 dimana n0 adalah suatu intejer berhingga dan bisa bernilai negatif. Jika demikian halnya, kesimpulan akhir menjadi S(n) benar untuk semua nilai

(30)

2.1 Prinsip Induksi Matematik 27

Disini yang akan dibuktikan hanya contoh nomor 1, pembuktian 5 nomor yang lainnya disisakan sebagai latihan.

(2) Langkah Induktif _! Diasumsikan S(k):

k

Contoh 2.2 Buktikan bahwa ₈n ₂Z+ _berlaku:

1. Jika n 3; maka 2n ₂_n_{+ 1}_:

2. 12_{+ 2}2₊_:::_{+ (}_n ₁₎2 _< n3 3 :

3. Jika n 10; maka 2n_{> n}3

Disini yang akan dibuktikan hanya contoh nomor 1, pembuktian 2 nomor lainnya disisakan sebagai latihan.

Bukti. MisalkanS(n): 2n ₂_n_{+ 1} _dengan _n ₃_:

(31)

(2)Langkah Induktif _!DiasumsikanS(k): 2k ₂_k_{+ 1} _benar_untuk

suatu k ₂ Z+ _dan _k ₃_: _{Akan dibuktikan bahwa} _S₍_k_{+ 1)} _{juga benar, ini} berarti harus dibuktikan

2k+1 ₂₍_k_{+ 1) + 1}_: Berdasarkan asumsi diketahui 2k ₂_k_{+ 1}_;_maka

2k_:₂ ₍₂_k_{+ 1)}_:₂

,

2k+1 (2k+ 1) + (2k+ 1)_, 2k+1 (2k+ 2) + 2k_,

2k+1 2(k+ 1) + 2k:

Karena k 3; maka2k 1: Jadi

2k+1 2(k+ 1) + 2k 2(k+ 1) + 1:

z Perhatikan dua prosedurpseudocode berikut ini.

PROSEDUR 1

procedure SumOfSquares1(n: positive integer) begin

sum:= 0

for i:= 1 ton do

sum:=sum+i2 end

PROSEDUR 2

procedure SumOfSquares1(n: positive integer) begin

sum:=n (n+ 1) (2 n+ 1)=6 end

Terlihat bahwa kedua prosedur di atas sama-sama menghitung jumlah kuadrat intejer positif dari 1 sampai dengan n. Karena Prosedur 1 meng-gunakan perintah loop for, maka total operasinya melibatkan n adisi dan

n multiplikasi (ini belum termasuk n 1 adisi untuk penambahan variabel

(32)

Contoh 2.3 Kita amati jumlah intejer positif ganjil berurutan berikut. 1) 1 = 1 (= 12₎

2) 1 + 3 = 4 (= 22₎

3) 1 + 3 + 5 = 9 (= 32₎

4) 1 + 3 + 5 + 7 = 16 (= 42₎

Dari4intejer positif pertama ini, kita dapatkan pola untuk membuat suatu

konjektur (suatu proposisi yang belum diketahui benar dan salahnya) yang berbunyi: Jumlah n intejer positif ganjil pertama yang berurutan adalah n2_; _{dengan kata lain,} ₈_n₂_Z+_;

Selanjutnya, buktikan kebenaran konjektur itu dengan prinsip induksi matem-atik.

Contoh 2.4 Diantara banyak barisan bilangan yang cukup menarik di dalam matematika diskret dan kombinatorika adalahbarisan bilangan harmonik:

H1; H2; H3; :::, dimana

(33)

dapat dirumuskan dengan

Teorema 2.2 (Bentuk Alternatif - Prinsip Induksi Berhingga) Mis-alkan S(n) menotasikan suatu pernyataan matematik terbuka yang meli-batkan satu atau lebih variabel intejer positif n; dan misalkan n0; n1 2 Z+

dengan n0 n1: Jika:

(34)

Contoh 2.5 Kita perhatikan barisan intejer a0; a1; a2; :::; dimana

a0 = 1; a1 = 2; a2 = 3; dan

an = an 1+an 2+an 3; 8n 2Z; n 3:

Buktikan bahwa ₈n ₂N; an 3n:

Bukti. MisalkanS0₍_n_): _a

n 3n;8n 2N:

Langkah Basis: Kita amati bahwa S0₍₀₎_{; S}0₍₁₎_; _dan _S0₍₂₎ _benar: (1)a0 = 1 = 30 30;

(2)a1 = 2 3 = 31; dan (3)a2 = 3 9 = 32:

Langkah Induktif: AndaikanS0₍₀₎_{; S}0₍₁₎_{; S}0₍₂₎_{; :::; S}0₍_k₎ _benar un-tuk suatu k ₂ N; dan k 2: Ini berarti k + 1 pernyataan berikut adalah benar

a0 30

a1 31

a2 32 ...

ak 3k

Berdasarkan asumsi tersebut, maka

ak+1 = ak+ak 1+ak 2 3k+ 3k 1+ 3k 2 3k+ 3k+ 3k = 3k+1:

z

Soal 2.1.1 Perhatikan empat persamaan berikut:

1 = 1 (1)

2 + 3 + 4 = 1 + 8 (2)

5 + 6 + 7 + 8 + 9 = 8 + 27 (3)

10 + 11 + 12 + 13 + 14 + 15 + 16 = 27 + 64 (4)

Buatlah konjektur rumus umum dari keempat persamaan di atas, dan buk-tikan kebenaran konjektur yang anda buat.

(35)

1. Untuk n= 3; misalkan X3 =f1;2;3g: Perhatikan jumlahan

dimanaPA adalah produk dari semua anggota subhimpunan tak-kosong

A dari X3: Evaluasi (tentukan nilai) jumlahan tersebut.

2. Ulangi perhitungan Soal 1: untuk s2 (dimana n = 2 dan X2 = f1;2g)

dan s4 (dimana n= 4 dan X2 =f1;2;3;4g)

3. Buatlah konjektur hasil umum yang digeneralisasi dari Soal 1: dan Soal

2:, kemudian buktikan kebenaran konjektur yang anda buat.

Soal 2.1.3 Untuk n ₂Z+_; _misalkan _H

n adalah bilangan harmonik ke-n:

1. Untuk semua n₂N; buktikan bahwa (1 + n

2) H2:

2. Untuk semua n₂N; buktikan bahwa

n

Untuk memahami de…nisi rekursif, terlebih dahulu perhatikan barisan intejer genap tak-negatif: 0; 2; 4; 6; 8; .... Barisan itu bisa kita tuliskan dengan:

bn= 2n;8n2N:Suku ke berapapun dari barisan itu bisa kita peroleh secara

langsung, misalnya: suku ke-125 adalah b125 = 250: Barisan yang demikian kita sebut dengan barisan dengan rumus eksplisit.

Sebagai badingannya, sekarang kita perhatikan barisan pada Contoh 2.5, untuk mendapatkan suku ke-k, yaitu ak; kita tidak mempunyai rumus

ek-splisit, sebagai gantinya dibutuhkan nilai tiga suku sebelumnya, yaitu ak 1;

ak 2; dan ak 3, sehingga ak = ak 1 +ak 2 +ak 3: Kemudian nilai ketiga suku itu, masing-masing juga membutuhkan nilai tiga suku sebelumnya lagi. Demikian seterusnya, pada akhirnya semua nilaiak;untukk 3;bergantung

(36)

2.2 De…nisi Rekursif 33

contoh tersebut: a0 = 1; a1 = 2; dan a2 = 3: Proses rekursi memberikan ni-lai suku berikutnya secara rekursif didasarkan pada nini-lai basis rekursi, pada contoh tersebut ak =ak 1+ak 2+ak 3:

De…nisi rekursif merupakan suatu jawaban ketika untuk menentukan ru-mus eksplisit suatu barisan sangat rumit atau bahkan ru-mustahil. Hal ini terjadi tidak hanya pada barisan bilangan, tetapi juga paling sering terjadi pada beberapa konsep matematika yang lain, seperti: operasi himpunan, proposisi dalam logika, relasi, fungsi, bahasa mesin, dll.

Contoh 2.6 Misalkan p1; p2; p3; ..., pn adalah n proposisi. Untuk

menen-tukan nilai kebenaran

p1 ^p2^p3^:::^pn;

dimanan 2;diperlukan konsep rekursif atas dasarhukum asosiatif kon-jungsi.

Basis Rekursi: p1^p2:

Proses Rekursi: Untuk n 2;

p1^p2^p3^:::^pn 1^pn,(p1 ^p2^p3^:::^pn 1)^pn

De…nisi rekursif berdasarkan hukum asosiatif pada contoh tersebut bisa diperumum melalui ilustrasi berikut ini. Ambil untuk kasus n = 4; maka

p1^p2^p3^p4 , (p1^p2 ^p3)^p4 , [(p1^p2)^p3]^p4 , (p1^p2)^(p3^p4) , p1^[p2^(p3^p4)] , p1^(p2 ^p3^p4):

Dari fakta ini dapat diambil suatu kesimpulan bahwa berdasarkan sifat asosi-atif tanda kurung bisa diletakkan secara bebas. Hasil ini dimantabkan secara lebih umum pada penyataan di dalam contoh berikut ini.

Contoh 2.7 Misalkan n ₂ Z+ _dengan _n ₃_; _{dan misalkan} _r ₂_Z+ _dengan 1 r < n:Maka, untuk sembarang proposisip1; p2; :::; pr; pr+1; ...; pn berlaku

(p1^p2^:::^pr)^(pr+1^:::^pn)

, p1^p2^:::^pr^pr+1^:::^pn:

(37)

dasar. Sekarang diasumsikan benar untukn=k dan untuk setiap1 r < k;

ini berarti berlaku

(p1^p2^:::^pr)^(pr+1^:::^pk)

, p1 ^p2^:::^pr^pr+1^:::^pk:

Berdasarkan asumsi ini harus dibuktikan benar untuk n =k+ 1 dan untuk setiap 1 r < k+ 1: Dalam hal ini perhatikan dua kasus berikut ini.

1. Jikar=k; berdasarkan de…nisi rekursif jelas berlaku

(p1^p2^p3^:::^pk)^pk+1 ,p1^p2^p3^:::^pk^pk+1: 2. Jika1 r < k;maka

(p1^p2^:::^pr)^(pr+1^:::^pk^pk+1) , (p1^p2^:::^pr)^[(pr+1^:::^pk)^pk+1] , [(p1^p2^:::^pr)^(pr+1^:::^pk)]^pk+1 , (p1^p2^:::^pr^pr+1^:::^pk)^pk+1 , p1^p2^:::^pr^pr+1^:::^pk^pk+1:

z

Contoh 2.8 Contoh 2.4 memenuhi pola pende…nisian rekursif:

Basis Rekursi: H1 = 1:

Proses Rekursi: Untuk n 1; Hn+1 =Hn+ _n₊₁1 :

Contoh 2.9 Menghitungn!untukn 0mengikuti pola pende…nisian rekur-sif:

Basis Rekursi: 0! = 1:

Proses Rekursi: Untuk n 0; (n+ 1)! = (n+ 1) (n!):

Contoh 2.10 Pende…nisian rekursif bilangan Fibonacci.

Basis Rekursi: F0 = 0; :F1 = 1

Proses Rekursi: Untuk n₂Z+ _dan _n ₂_;

Fn=Fn 1+Fn 2

(38)

Contoh 2.11 Pada Bab 1 telah diperkenalkan koe…sien binomial n_r untuk

n; r ₂Ndengan 0 r n:Berikut ini diberikan pede…nisian secara rekursif,

n+ 1

Berdasarkan de…nisi rekursif ini, penentuan nilai n_r ;dimana0 n 4dan

0 k n dapat dinyatakan dalam tabel segitiga Pascal:

n k

Berdasarkan de…nisi rekursif ini, penentuan nilai am;k; dimana 1 m 5

dan 0 k m 1 dapat dinyatakan dalam tabel berikut.

(39)

Dari tabel ini didapat suatu pola bahwa jumlah baris ke-m adalah m!:

Secara umum, buktikan bahwa untuk suatum ₂Z+_;_berlakuPm 1

k=0 am;k =m!:

Dari fakta ini, dan berdasarkan induksi matematik, jika diasumsikan

m 1

Soal 2.2.1 Barisan intejer a1; a2; a3; :::dide…nisikan secara eksplisit dengan

rumus an= 5n untuk n2Z+; dapat juga secara rekursif

a) a1 = 5; dan

b) an+1 =an+ 5; untuk n 1:

Barisan intejer b1; b2; b3; ::: dide…nisikan secara eksplisit dengan rumus

(40)

a)’ b1 = 3; dan

b)’ bn+1 =bn+ 2n+ 3; untuk n 1:

Buatlah de…nisi rekursif untuk setiap barisan intejer c1; c2; c3; ::: berikut

ini, dimana untuk n ₂Z+_;

1. cn= 7n:

2. cn= 7n:

3. cn= 3n+ 7:

4. cn= 7:

5. cn=n2:

6. cn= 2 ( 1)n:

Soal 2.2.2

1. Buatlah de…nisi rekursif untuk dijungsi dari proposisi p1; p2; p3; :::pn+1;

n 1:

2. Buktikan bahwa jika n; r ₂Z+_; _dengan _n ₃ _dan ₁ _{r < n;} _maka

(p1_p2_:::_pr)_(pr+1_pr+2_:::_pn)

, p1_p2_:::_pr_pr+1_:::_pn:

Soal 2.2.3

1. Bangunlah suatu de…nisi rekursif untuk adisi (jumlahan) dari n bilan-gan nyata x1; x2; :::; xn; dimana n 2:

2. Berdasarkan hukum asosiatif untuk adisi bilangan nyata, buktikan bahwa jika n; r ₂Z+_; _dengan _n ₃ _dan ₁ _{r < n;} _maka

(41)

Soal 2.2.4 Perhatikan bahwa untuk setiap x; y ₂R;

Soal 2.2.6 Misalkan Fn adalah bilangan Fibonacci ke-n:

1. untuk n 0; buktikan bahwa

n

P

i=0

Fi =Fn+2 1:

2. untuk n 1; buktikan bahwa

(42)

2.3 Algoritma Pembagian 39

Walaupun Ztidak tertutup terhadap pembagian, namun ada beberapa inte-jer yang dapat dibagi oleh inteinte-jer yang lain.

De…nisi 2.1 Misalkana; b₂Z; dan b₆= 0: Kita sebut b membagia; ditulis

b _j a; jika ada intejer n sehingga a = bn: Dalam hal ini b disebut juga

pembagi/faktor dari a atau a disebut kelipatan dari b: Dalam hal b tidak membagi a dinotasikan denganb -a:

Sebagai ilustrasi, 7 _j 42 karena 42 = 7:6; sedangkan 7 - 18 karena tidak ada n ₂ Z sehingga 18 = 7n: Terkait dengan pengertian pembagian, suatu sifat yang cukup penting yang dimiliki olehZadalah bahwaZtidak memuat pembagi nol, artinya

(₈a; b₂Z)ab= 0 ₎a= 0_{_}b = 0;

atau lebih mudah dimegerti kotraposisinya

(₈a; b₂Z)a₆= 0_^b ₆= 0₎ab₆= 0;

Teorema 2.3 (Sifat-sifat Dasar Pembagian) Untuk semua a; b; c ₂ Z;

berlaku:

1. 1_ja dan a_j0:

2. [(a_jb)_^(b _ja)]₎a = b:

3. [(a_jb)_^(b _jc)]₎a_jc:

(43)

5. (x=y+z)_^((a_jx)_^(a_jy))₎a _jz:

6. (₈a; b₂Z+_{) (}_a_j_b₎₎_a _b:

7. Untuk 1 i n; misalkan ci 2Z: Jika ajci; maka

a_jc1x1+c2x2+:::+cnxn

dimana xi 2Z untuk setiap 1 i n:

Bukti. Disini hanya akan dibuktikan yang No. 4, lainnya disisakan sebagai latihan. a _j b dan a _j c; berarti ada m; n ₂ Z sehingga b = ma

dan c=na: Dengan demikian untuk setiapx; y ₂Z berlaku xb =xma dan

yc=yna:Akibatnya,

bx+cy = xma+yna

= (xm+yn)a;

dan ini berarti a_j(bx+cy): z

Contoh 2.13 Adakah x; y; z ₂ Z yang memenuhi persamaan 14x+ 21y

7z = 64:

Jawab. Perhatikan bahwa 7_j14; 7_j21 dan 7_j( 7); maka berdasarkan Teorema 2.3 (No 7),7_j(14x+ 21y 7x):Dilain pihak7-64;kesimpulannya

tidak ada x; y; z ₂Zyang memenuhi persamaan 14x+ 21y 7x= 64: z

Contoh 2.14 Misalkan a; b₂Z sehingga 2a+ 3b merupakan kelipatan dari

17: Buktikan bahwa 17_j9a+ 5b:

Bukti. Perhatikan bahwa17_j2a+ 3b ₎17_j( 4)(2a+ 3b);di lain pihak 17_j17a+ 17b: Dengan demikian

17 _j [( 4)(2a+ 3b) + (17a+ 17b)]_, 17 _j (9a+ 5b):

(44)

Teorema 2.4 (Algoritma Pembagian) Jika a; b₂Z dengan b >0; maka ada tepat satu q; r ₂Z sehingga

a =qb+r; 0 r < b:

Dalam hal ini a disebut yang dibagi, b adalah yang membagi, q adalah

hasil bagi, dan r adalah sisa pembagian. Selanjutnya sisa pembagian dinotasikan dengan r=a mod b dan hasil bagi dinotasikan q=a div b:

Fakta bahwa misalkan a; b₂Z; b₆= 0;maka

a div b = _ba

bc; dan a mod b = a b:_ba

bc;

notasi _bx_c mengartikan bilangan bulat terbesar yang x:

Contoh 2.15 Berdasarkan algoritma pembagian, berikut ini diberikan beber-apa ilustrasi.

1. Misalkan a= 67 dan b= 7; maka

q =_b67

7 c= 9 dan r= 67 7:9 = 4:

q =_b48

6 c= 8 dan r= 48 6:8 = 0:

q=_b 72

11 c= 7 dan r= ( 72) (11)( 7) = 5:

4. Misalkan a; b₂Z+_:

(a) Jika a = qb untuk suatu q ₂ Z+_; _maka _a _{= (} _q₎_b: _{Dalam hal}

(45)

(b) Jika a=qb+r untuk suatu q₂N dan 0< r < b; maka

Untuk lebih jelasnya, proses mendapatkanq danr dalam algoritme pem-bagian dirinci dengan pseudocode dalam Prosedur 3.

PROSEDUR 3

Salah satu penerapan algoritma pembagian adalah digunakan untuk men-gubah sistem basis bilangan, misalnya: desimal ke biner, oktal, heksadesimal, dll. Lengkapnya hal ini dinyatakan pada bagian berikut ini.

2.3.1 Representasi Basis

Intejer positif dapat direpresentasikan dalam berbagai cara, namun paling umum dipakai adalah sistem desimal atau sistem basis 10. Jadi apabila diberikan suatu intejer positif tanpa keterangan apapun, maka yang di-maksud adalah intejer tersebut memiliki representasi basis 10. Misalnya

a = 1367; ini berarti

(46)

Sistem lain yang cukup populer adalah sistem biner atau representasi basis 2 yang dipakai dalam kerja mesin komputasi. Misalnya a = 110101 basis 2;

ini berarti

a= 1:25 _{+ 1}_:₂4_{+ 0}_:₂3_{+ 1}_:₂2_{+ 0}_:₂1_{+ 1}_:₂0_:

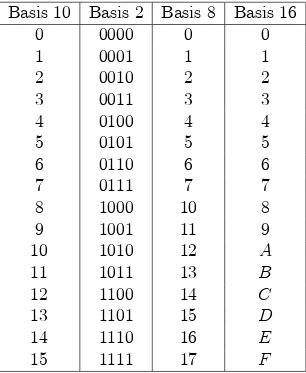
Tabel berikut ini mengilutrasikan hubungan antara sistem representasi desi-mal, biner, oktal (basis 8), dan heksadesimal (basis 16) untuk intejer dari 0 sampai15:Faktanya keempat sistem inilah yang paling sering dipakai dalam bidang terapan, khususnya ilmu komputer.

Basis 10 Basis 2 Basis8 Basis 16

0 0000 0 0

1 0001 1 1

2 0010 2 2

3 0011 3 3

4 0100 4 4

5 0101 5 5

6 0110 6 6

7 0111 7 7

8 1000 10 8

9 1001 11 9

10 1010 12 A

11 1011 13 B

12 1100 14 C

13 1101 15 D

14 1110 16 E

15 1111 17 F

Secara umum representasi basis dari suatu intejer dinyatakan dalam de…nisi berikut ini.

De…nisi 2.2 Jikab 2 adalah suatu intejer, maka sembarang intejer positf

a dapat diekspresikan secara tunggal sebagai

a =anbn+an 1bn 1 +:::+a1b+a0; (2.1)

dimana 0 ai < b untuk i= 0;1; :::; n dan an 6= 0: Ruas kanan Persamaan

2.1 disebut representasi basis b dari a; dan dinotasikan dengan

a= (anan 1:::a1a0)b:

Selanjutnya dari de…nisi di atas, intejerai;untuk0 i n; disebutdijit.

(47)

rendah. Catatan bahwa jikab = 10; representasia cukup ditulis

a =anan 1:::a1a0:

Banyaknya dijit dariadisebut denganpresisi ataupanjang daria:Dalam de…nisi di atas terlihat bahwa presisi dari a adalah n: Jika n = 0; maka a

disebutintejer presisi tunggal. Sedangkan jikan > 0;makaadisebut sebagai

intejer presisi ganda.

Dari De…nisi 2.2, berikut ini diberikan prosedur untuk mengubah repre-sentasi basis-b dari intejer a kebentuk standar desimal daria:

PROSEDUR 4

procedure ChangeDecimal((anan 1:::a1a0)b :intejer)

begin

a:= 0

for i:= 0 ton do

a:=a+aibi

return(a) end

Contoh 2.16 Misalkan (1110101)2 adalah representasi basis-2 dari intejer

a: Tentukan intejera:

Jawab. Nilai intejer a adalah

(1110101)2 = 1:26+ 1:25+ 1:24+ 0:23+ 1:22 + 0:21+ 1:20 = 64 + 32 + 16 + 0 + 4 + 0 + 1

= 117:

z Dalam langkah-langkah berikut ini perhatikan bahwa algoritma pemba-gian melandasi sistem perubahan representasi basis.

1. Persamaan (2.1) dapat dituliskan sebagai

a= (anbn 1+an 1bn 2+:::+a2b+a1)b+a0:

Ini berarti a0 merupakan sisa dari a dibagi oleh b: Dalam hal ini hasil baginya adalah

(48)

2. Persamaan (2.2) dapat dituliskan sebagai

q1 = (anbn 2+an 1bn 3+:::+a3b+a2)b+a1:

Ini berarti a1 merupakan sisa dariq1 dibagi oleh b: Dalam hal ini hasil baginya adalah

q2 =anbn 2+an 1bn 3+:::+a3b+a2 (2.3) 3. Persamaan (2.3) dapat dituliskan sebagai

q2 = (anbn 3+an 1bn 4+:::+a4b+a3)b+a2:

Ini berarti a2 merupakan sisa dariq2 dibagi oleh b: Dalam hal ini hasil baginya adalah

q3 =anbn 3+an 1bn 4+:::+a4b+a3

4. Proses berlanjut sampai didapatkan an merupakan sisa dari qn dibagi

oleh b dan hasil baginya adalah0:

Contoh 2.17 Nyatakan intejer a= 938 sebagai representasi:

1. basis 8; dan

2. basis 2:

3. basis 16:

Jawab. Berdasarkan uraian di atas perhatikan proses berikut ini.

(49)

3. Algoritme representasi basisbdinyatakan dalam prosedur berikut dengan input intejer a 0 dan b 2:

PROSEDUR 5

procedure Basis-bRepresetation(a, b:intejer positif) begin

Intejer negatif dapat direpresentasikan dalam beberapa cara. Dua diantaranya akan dibahas dalam tulisan ini, yaitu: representasi besaran-bertanda dan rep-resentasi komplemen.

Representasi Besaran-bertanda

Tanda dari suatu intejer (baik positif maupun negatif) danbesarannya (nilai mutlak) direprsentasikan sebagairepresentasi besaran-bertanda. Intejer posi-tif diberi suatu tanda dijit0;sementara intejer negatif diberi suatu tanda dijit

b 1:Untuk suatu representasi basis-bbedijitn (berupa barisan) terdiri dari:

(50)

Barisan Besaran- Barisan Besaran-Bertanda

Besaran-0111 7 1111 7

0110 6 1110 6

0101 5 1101 5

0100 4 1100 4

0011 3 1011 3

0010 2 1010 2

0001 1 1001 1

0000 0 1000 0

Representasi Komplemen

Penjumlahan dan pengurangan representasi komplemen tanpa perlu me-meriksa dijit tanda. Intejer tak-negatif dalam selang [0; bn _1]

direpresen-tasikan sebagai barisan basis-b dengan panjang dijit n dan dijit order tinggi 0: Misalkanx adalah intejer positif yang direpresentasikan sebagai barisan

(xn; xn 1; :::; x1; x0)b

dimana xn= 0:Maka x direpresentasikan sebagai barisan

(xn; xn 1; :::; x1; x0) + 1

dimana xi = b 1 xi dan + adalah jumlahan standar. Sebagai ilustrasi,

berikut ini diberikan tabel representasi komplemen untuk biner dari intejer dalam selang [ 7;7]:

Barisan Komple- Barisan Komple-mennya 2 mennya 2

0111 7 1111 1

0110 6 1110 2

0101 5 1101 3

0100 4 1100 4

0011 3 1011 5

0010 2 1010 6

0001 1 1001 7

0000 0 1000 8

Soal 2.3.1

1. Jika a; b; c₂Z+ _dan _a_j_bc; _{apakah dapat disimpulkan bahwa} _a_j_b _atau

(51)

2. Untuk setiapa; b; c₂Z;buktikan bahwa jikaa-bc;makaa-b dana-c:

3. Misalkan a; b ₂ Z+_: _Jika _b _j _a _dan _b _j ₍_a_{+ 2)}_; _{buktikan bahwa} _b _{= 1}

atau b= 2:

4. Jika n ₂Z+ _dan _n _{ganjil, buktikan bahwa} ₈_j₍_n2 ₁₎_:

5. Jika a; b₂Z+ _{dan keduanya ganjil, buktikan bahwa} ₂_j₍_a2₊_b2₎ _tetapi 4-(a2₊_b2₎_:

6. Jika n ₂N; buktikan bahwa 3_j(7n ₄n₎_:

Soal 2.3.2 Tentukan hasil bagi q dan sisa r dari pembagian a oleh b yang diketahui berikut ini.

1. a= 23 dan b= 7:

2. a= 115 dan b= 12:

3. a= 0 dan b = 42:

4. a= 434 dan b= 31:

Soal 2.3.3 Tuliskan intejer berbasis-10berikut ini ke dalam basis-2, basis-4;

dan basis-8:

a) 137 b) 6243 c) 12:345.

Soal 2.3.4 Tuliskan intejer berbasis-10berikut ini ke dalam basis-2dan

basis-16:

a) 22 b) 527 c) 1234 d) 6923.

Soal 2.3.5 Konversikan masing-masing dari bilangan heksadesimal berikut ini ke dalam bilangan basis-10 dan basis-2:

a) A7 b) 4C2 c) 1C2B d) A2DF E.

Soal 2.3.6 Konversikan masing-masing dari bilangan biner berikut ini ke dalam bilangan basis-10 dan basis-16:

a) 11001110 b) 00110001 c) 11110000 d) 01011110.

Soal 2.3.7 Tuliskan masing-masing dari bilangan biner berikut ini ke dalam representasi komplemen dua, hasilnya mengikuti pola 8-bit.

(52)

2.4 Algoritme Euclid 49

Soal 2.3.8 Jika suatu mesin menyimpan intejer dengan metode komplemen dua, berapa intejer terbesar dan terkecil yang dapat disimpan apabila meng-gunakan pola 8-bit.

a) 4-bit b) 8-bit c) 16-bit d) 32-bit e) 2n-bit, n₂Z+ Soal 2.3.9 Dide…nisikan himpunan X Z+ _{secara rekursif sebagai berikut:}

a) 3₂X; dan

b) jika a; b₂X; maka a+b ₂X:

Buktikan bahwaX =_f3k k₂Z+_g_;_{himpunan semua intejer positif yang}

habis dibagi 3:

Soal 2.3.10 Misalkan n₂Z+ _dengan

n =rk:10k+:::+r2:102 +r1:10 +r0:

Buktikan bahwa

1. 2_jn jika dan hanya jika2_jr0:

2. 4_jn jika dan hanya jika(r1:10 +r0):

3. 8_jn jika dan hanya jika(r2:102+r1:10 +r0):

Buatlah generalisasi dari hasil tersebut.

2.4 Algoritme Euclid

Bahasan yang diberikan pada bagian ini dan pada bagian berikutnya meru-pakan landasan dasar dari teori bilangan. Berapa teorema dan sifat-sifat diberikan tanpa disertai bukti dengan alasan bahwa seluruh materinya akan dibahas lebih rinci di matakuliah Pengantar Teori Bilangan.

De…nisi 2.3 Untuk a; b ₂ Z, suatu intejer positif x dikatakan pembagi bersama dari a dan b jika x _j a dan x _j b: Selanjutnya, untuk a dan b

tidak keduanya nol, c₂Z+ _disebut _{pembagi bersama terbesar}_dari _a _dan

b; dinotasikan dengan c = gcd (a; b); jika c adalah yang terbesar diantara semua pembagi bersama dari a dan b, atau dengan kata lain

c= max_fx₂Z+ ₍_x

(53)

Teorema 2.5 Misalkan c = gcd (a; b): Jika pembagi bersama d dari a dan

b; maka d_jc:

Teorema 2.6 Untuk setiap a; b ₂ Z+_; _{ada tepat satu} _c ₂ _Z+ _sehingga _c₌ gcd (a; b): Selanjutnya ada x; y ₂ Z sehingga c = xa+yb (c adalah suatu kombinasi linear dari a dan b):

Sifat-sifat dasar dari pembagi bersama terbersar dapat dirinci sebagai berikut. Misalnya c= gcd (a; b);maka:

1. c adalah intejer positif terkecil dari himpunan_fxa+yb=x; y₂Zg:

2. Jikad=sa+tb untuk suatus; t ₂Z;maka c_jd:

Intejer a dan bdisebut prima relatif jika gcd (a; b) = 1; selanjutnya ada

x; y ₂Z sehinggaxa+yb= 1:

Contoh 2.18 Karena gcd (42;70) = 14; maka adax; y ₂Z; sehingga

42x+ 70y= 14_,3x+ 5y= 1:

Mudah diperiksa bahwa x = 2 dan y = 1 adalah solusinya. Kemudian untuk k ₂Z;

3(2 + 5k) + 5( 1 3k) = 1;

juga

42(2 5k) + 70( 1 + 3k) = 14:

Jadi nilai x dan y tidak tunggal.

Teorema 2.7 (Algoritme Euclid) Misalkan a; b ₂ Z+_; _{jika dengan}

algo-ritme pembagian berlaku langkah-langkah berikut ini:

(54)

Contoh 2.19 Dengan algoritma Euclid, tentukan gcd(250;111); kemudian tentukan x; y ₂Z sehingga gcd(250;111) = 250x+ 111y:

Jawab. Perhatikan langkah-langkah berikut ini.

Langkah ke-1 250 = 2(111) + 28 0<28<111 Langkah ke-2 111 = 3 (28) + 27 0<27<28 Langkah ke-3 28 = 1(27) + 1 0<1<27 Langkah ke-4 27 = 27(1) + 0

Maka gcd(250;111) = 1:Perhatikan bahwa langkah-langkah algotima Euclid bisa diringkas penulisannya dengan menggunakan sifat-sifat gcd berikut

gcd(250;111) = gcd(111;28) = gcd(28;27) = gcd(28;27) = gcd(27;1) = gcd(1;0) = 1:

Selanjutnya, untuk mendapatkan kombinasi linearnya kita lakukan langkah balik. Perhatikan pada Langkah ke-3:

1 = 28 1 (27)

= 28 1 (111 3 (28))

= ( 1) (111) + (4) (28)

= ( 1) (111) + (4) (250 2 (111)) = (4) 250 + ( 9) (111):

Secara umum, untuk k₂Z;

1 = (4 111k) 250 + ( 9 + 250k) 111:

(55)

PROSEDUR 6

procedure gcd(a; b: intejer positif, a b) begin

r :=a mod b d:=b

while r >0 do begin

c:=d d:=r

r :=c modd

end return(d) end

De…nisi 2.4 Misalkan a; b ₂ Z: Suatu interjer positif x disebut kelipatan bersamadariadanbjikaxadalah kelipatan dari keduaadanb;atau dengan kata lain

(a_jx)_^(b _jx)

Untuka danb semuanya tak nol,cdisebutkelipatan bersama terkecildari

a dan b; dinotasikan c = lcm (a; b); jika c adalah yang terkecil dari semua kelipatan bersama dari a dan b; atau dengan kata lain

c= min_fx₂Z+ ₍_a

jx)_^(b _jx)_g:

Sifat-sifat dasar dari kelipatan bersama terkecil dinyatakan sebagai berikut.

1. ₈n ₂Z+_; _berlaku

lcm(1; n) = lcm(n;1) = n:

2. ₈a; n₂Z+_; _berlaku

lcm(a; na) =na:

3. Jikaa; m; n₂Z+ _dengan _m _n; _maka

lcm(am_{; a}n_{) =} _an _dan _gcd(_am_{; a}n_{) =} _am_:

Teorema 2.8 Misalnya c= lcm (a; b):Jikay adalah kelipatan bersama dari

(56)

Teorema 2.9 Untuk a; b₂Z+_;

ab= lcm (a; b):gcd (a; b):

Jelas bahwa, jika a dan b adalah prima relatif, maka

lcm (a; b) =ab:

Contoh 2.20 Tentukan lcm(168;456):

Jawab. Periksalah bahwa gcd(168;456) = 24: Akibatnya,

lcm(168;456) = (168)(456)

24 = 3192:

z Algoritme Euclid dapat diperluas sehingga tidak hanya mengasilkan pem-bagi bersama terbesar dari dua intejer a dan b; tetapi juga menghasilkan intejer x dan y yang memenuhiax+by =d; diberikan dalam Prosedur 7.

PROSEDUR 7

procedure gcd(a; b: intejer positif, positif, a b) begin

if b= 0 then begin

d:=a; x:= 1; y := 0 return(d; x; y) end

x2 := 1; x1 := 0; y2 := 0; y1 := 1 while b >0 do

begin

q :=_ba

bc; r :=a qb; x:=x2 qx1; y :=y2 qy1

a:=b; b:=r; x2 :=x1; x1 :=x; y2 :=y1; y1 :=y end

d:=a; x:=x2; y :=y2 return(d; x; y)

end

Contoh 2.21 Gunakan Prosedur 7 untuk untuk menentukan gcd(a; b), x, dan y, sehingga gcd(a; b) =ax+by jika diketahui a = 4864 dan b= 3458:

(57)

(4864)(32) + (3458)( 45) = 38:

q r x y a b x2 x1 y2 y1

4864 3458 1 0 0 1

1 1406 1 1 3458 1406 0 1 1 1

2 646 2 3 1406 646 1 2 1 3

2 114 5 7 646 114 3 5 3 7

5 76 27 38 114 76 5 27 7 38

1 38 32 45 76 38 27 32 38 45

2 0 91 28 38 0 32 91 45 128

z Catatan bahwa jawaban dengan tabel pada contoh di atas dapat diseder-hanakan sebagai berikut, demi perhitungan menggunakan pensil dan kertas.

i qi+1 ri xi yi

0 4864 1 0

1 1 3458 0 1

2 2 1406 1 1

3 2 646 2 3

4 5 114 5 7

5 1 76 27 38

6 2 38 32 45

7 0

Perhatikan bahwa isian awal tabel ini adalah r0 =a; x0 = 1; y0 = 0; r1 =b;

x1 = 0; dan y1 = 1:Isian selanjutnya dihitung:

qi = b

ri 1

ri c

; untuki 1;

xi = xi 2 qi 1:xi 1; untuk i 2; dan

yi = yi 2 qi 1:yi 1; untuki 2:

Jika rs = 0; maka proses berhenti. Dalam hal ini gcd(a; b) =rs 1; x=xs 1, dan y =ys 1:

De…nisi 2.5 Intejer positif p disebut prima jika faktor dari p hanyalah 1

dan dirinya sendiri p: Intejer positif yang bukan prima disebutkomposit.

Dari de…nisi tersebut jelas bahwa suatu intejer positifpadalah prima jika memenuhi

(58)

Suatu intejer positif n adalah komposit jika

(₉n1; n2 2Z; 1< n1 < n; 1< n2 < n)n =n1n2:

Sebagai ilutrasi, barisan prima dapat ditulikan

2;3;5;7;11;13;17; :::

Lemma 2.1 Jikan₂Z+ _{adalah komposit, maka ada prima}_p_sehingga_p_j_n:

Bukti. Andaikan ada komposit n yang tidak mempunyai faktor prima, dan de…nisikan himpunanSyang anggotanya semua komposit ini, maka jelas bahwaS ₆=?:Berdasarkan prinsip keterurutan dengan baik, makaSmemuat unsur terkecil, sebut saja s: Karena s komposit, maka ₉s1; s2 2 Z; dengan 1 < s1 < sdan1 < s2 < ssehingga s = s1s2: Karena s tidak mepunyai faktor prima, maka s1 dan s2 haruslah juga tidak mempunyai faktor prima. Akibatnya, s1; s2 2 S; suatu kontradiksi, karena s adalah terkecil di dalam

S: Kesimpulannya,S =? atau n mempunyai faktor prima. z

Lemma 2.2 Jika p prima dan p_jab; maka p_ja atau p_jb:

Lemma 2.3 Misalkan ai 2 Z+ untuk setiap 1 i n: Jika p prima dan

p_ja1a2:::an; maka pjai untuk suatu 1 i n:

Teorema 2.10 (Teorema Dasar Aritmatika) Setiap intejer n 2 dapat di-faktorisasikan secara tunggal sebagai produk kuasa prima:

n =pe1 1 p

e2 2 :::p

ek

k ;

dimana pi prima berbeda dan ei intejer positif.

Ilustrasi untuk teorema di atas: 63 = 32_:₇_; _{100 = 2}2_:₅2_; _{4864 = 2}8_:₁₉_; 3458 = 2:7:13:19:

Contoh 2.22 Tentukan faktorisasi intejer 980220:

Jawab. Perhatikan langkah-langkah berikut ini

980220 = 21(490110) = 22(245055) = 2231(81685)

= 223151(16337) = 223151171(961) = 223151171312:

(59)

Contoh 2.23 Misalkan n₂Z+ _dan

10:9:8:7:6:5:4:3:2:n= 21:20:19:17:16:15:14:

Tunjukkan bahwa 17_jn:

Jawab. Perhatikan bahwa karena17 membagi ruas kanan, maka

17_j10:9:8:7:6:5:4:3:2:n:

Dari fakta ini dan karena 17- 10; 17- 9; 17 - 8; 17 - 7; 17 - 6; 17 -5; 17 -4;

17 - 3; dan 17- 2; berdasarkan Lemma 2.3 maka dapat disimpulkan bahwa

17_jn: z

Soal 2.4.1 Untuk masing-masing dari pasangan a; b ₂ Z+ _{berikut ini,}

ten-tukan gcd(a; b) dan nyatakan sebagai kombinasi linear dari a; b:

a) a= 231; b= 1820 b) a= 1369; b= 2597 c) a = 2689; b= 4001.

Soal 2.4.2

1. Untuk a; b₂Z+ _dan _d_{= gcd(}_{a; b}₎_; _{buktikan bahwa}

gcd(a

d; b d) = 1

2. Untuk a; b; n₂Z+ _dan _d _{= gcd(}_{a; b}₎_; _{buktikan bahwa}

gcd(na; nb) = n:gcd(a; b)

3. Misalkan a; b; c₂Z+ _dengan _c_{= gcd(}_{a; b}₎_; _{buktikan bahwa}

c2 _jab:

4. Untuk a; b; c; d₂Z+_; _{buktikan bahwa jika} _d₌_a₊_bc; _maka

gcd(b; d) = gcd(a; b):

5. Misalkan a; b; c₂Z+ _dengan _gcd(_{a; b}_{) = 1}_: _Jika _a_j_bc; _{buktikan bahwa}

a_jc:

matematika diskrit (1) Filsafat Matematika (1) Filsafat Matematika (1)

Sugi Guritman

Prapto Tri Supriyo

Departemen Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

BOGOR

2004

Contents

Chapter 1

Prinsip Dasar Mencacah

1.1

Aturan Jumlah dan Kali

1.2

Permutasi

1.3

Kombinasi

1.4

Kombinasi dengan pengulangan

Chapter 2

Sifat Dasar Intejer

2.1

Prinsip Induksi Matematik

2.3.1

Representasi Basis

2.4

Algoritme Euclid