METODE TITIK-INTERIOR PADA PEMROGRAMAN KUADRATIK KONVEKS

i

METODE TITIK-INTERIOR

PADA PEMROGRAMAN KUADRATIK KONVEKS

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh: Fenny Basuki NIM: 083114003

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

INTERIOR-POINT METHODS

IN CONVEX QUADRATIC PROGRAMMING

Research

Presented as Partial Fulfillment of the Requirements To Obtain the Sarjana Sains Degree

In Mathematics

By: Fenny Basuki

Student Number: 083114003

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY YOGYAKARTA

! "#

viii ABSTRAK

Penyelesaian pemrograman kuadratik konveks secara analitik memerlukan langkah yang panjang. Pada skripsi ini akan dipaparkan metode numerik yang dapat digunakan untuk menyelesaikan permasalahan tersebut, yakni metode titik-interior primal-dual. Metode titik-interior primal-dual merupakan suatu metode untuk menemukan penyelesaian primal-dual dengan menerapkan metode Newton dan memodifikasi arah selidik dan panjang langkah. Tujuan dari metode ini adalah membatasi pergerakan nilai optimum yang dihasilkan pada setiap iterasinya dengan toleransi tertentu. Pencarian penyelesaian optimum dimulai dari sebarang titik-interior, sehingga konvergensinya cepat diperoleh.

Kata kunci: Karush Kuhn Tucker, metode titik-interior primal-dual, pemrograman kuadratik konveks, penyelesaian optimum.

ix ABSTRACT

Solving the convex quadratic programming need a long step when it is finished analytically. In this thesis, numerical method will be introduced which can be used to solve this problem, namely a primal-dual point method. Primal-dual interior-point method is a method to find the primal-dual solution by applying Newton method and modifying the search direction and step-length. This method purpose to restricting the movement of the optimum value generated from each iteration method with certain tolerances. Optimum solution search start from the any interior-point so that the convergence will be faster to obtain.

x

KATA PENGANTAR

Puji syukur kepada Tuhan Yesus atas anugerah dan karunia-Nya sehingga penulisan skripsi ini dapat terselesaikan. Skripsi ini berjudul: “METODE TITIK-INTERIOR PADA PEMROGRAMAN KUADRATIK KONVEKS”_{, yang} diajukan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Matematika, Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma Yogyakarta.

Penulisan skripsi ini tidak lepas dari bantuan dan dukungan dari berbagai pihak. Oleh karena itu, dengan segala kerendahan hati penulis ingin menyampaikan ucapan terima kasih kepada:

1. Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen pembimbing dan Kaprodi Matematika FST-USD yang dengan rendah hati mau meluangkan banyak waktu dan penuh kesabaran telah membimbing penulis selama penyusunan skripsi. 2. P. H. Prima Rosa, S.Si., M.Sc., selaku Dekan FST-USD.

3. MV. Any Herawati, S.Si., M.Si., selaku dosen pembimbing akademik dan dosen penguji.

4. Dominikus Arif Budi Prasetyo, S.Si., M.Si., selaku dosen penguji.

5. A. Prasetyadi, S.Si., M.Si., dan Prof. Drs. R. Soemantri yang telah banyak membantu dan memberi masukan kepada penulis.

xii

DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

HALAMAN PERSEMBAHAN ... vi

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... vii

ABSTRAK ... viii

ABSTRACT ... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xii

DAFTAR GAMBAR ... xiv

DAFTAR TABEL ... xv

BAB I PENDAHULUAN ... 1

A. Latar Belakang Masalah ... 1

B. Perumusan Masalah ... 4

C. Batasan Masalah ... 5

D. Tujuan Penulisan ... 5

E. Manfaat Penulisan ... 5

F. Metode Penulisan ... 5

G. Sistematika Penulisan ... 6

xiii

A. Matriks dan Ruang Vektor ... 8

B. Fungsi Terdiferensial ... 41

C. Himpunan Konveks dan Fungsi Konveks ... 55

D. Teori Optimisasi ... 72

E. Metode Newton untuk Sistem Persamaan Nonlinear ... 85

BAB III METODE TITIK-INTERIOR ... 91

A. Pemrograman Kuadratik Konveks ... 91

B. Metode Titik-Interior ... 94

BAB IV PENUTUP ... 120

A. Kesimpulan ... 120

B. Saran ... 121

DAFTAR PUSTAKA ... 122

xiv

DAFTAR GAMBAR

Halaman

Gambar 1.1.1Minimum sama dengan maksimum ... 2

Gambar 2.1.1 Lingkaran 1 ... 30

Gambar 2.1.2 Himpunan Terurut ... 38

Gambar 2.2.1 Teorema Nilai Rata-Rata ... 45

Gambar 2.3.1 Ilustrasi dari Himpunan Konveks ... 56

Gambar 2.3.2 Lingkaran x2₊y2 ₌1 ... 57

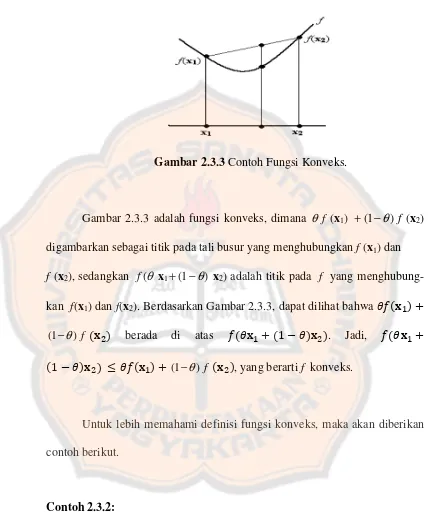
Gambar 2.3.3 Contoh Fungsi Konveks ... 58

xv

DAFTAR TABEL

Halaman

Tabel 3.2.1 Output Penyelesaian Contoh 3.2.1 dengan Matlab ... 117

Tabel 3.2.2 Tabel Perbandingan Nilai Awal Metode Titik-Interior

1 BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Saat ini semakin banyak permasalahan pada kehidupan sehari-hari yang memerlukan pendekatan optimisasi dalam penyelesaiannya. Sebagai contoh, misalkan sebuah perusahaan ingin meminimumkan biaya pembuatan dua produk. Untuk menyelesaikan permasalahan ini, maka harus diketahui hal-hal apa saja yang mempengaruhi pembuatan dua produk tersebut, misal-nya jumlah bahan baku yang tersedia. Misalkan, meminimumkan biaya pem-buatan dua produk dinyatakan dengan fungsi f . Sedangkan, banyaknya barang yang dihasilkan dari masing-masing produk, misalnya , . Variabel-variabel tersebut perlu diberi batasan yang disebut dengan kendala, dalam hal ini berupa jumlah bahan baku yang tersedia, sedangkan fungsi , di-sebut dengan fungsi obyektif.

Untuk lebih jelasnya, perhatikan Gambar 1.1.1:

Gambar 1.1.1 Minimum sama dengan maksimum

Berdasarkan Gambar 1.1.1, (dalam hal ini sebagai contoh adalah

suatu fungsi dengan satu variabel) dapat dilihat bahwa jika suatu titik me-nunjukkan nilai pembuat minimum dari fungsi , maka titik yang sama itu juga menunjukkan nilai pembuat maksimum dari negatif fungsi tersebut,

yak-ni .

persamaan. Sedangkan, permasalahan optimisasi tidak berkendala adalah op-timisasi suatu fungsi obyektif tanpa kendala.

Secara garis besar, permasalahan dalam teknik optimisasi dapat berupa permasalahan pemrograman linear maupun nonlinear. Pemrograman linear adalah pemrograman yang mempelajari kasus dimana fungsi obyektifnya ada- lah fungsi linear dan kendalanya merupakan persamaaan atau pertidaksamaan linear. Sedangkan, pemrograman nonlinear adalah pemrograman yang mem-pelajari kasus dimana salah satu fungsi obyektif atau fungsi kendalanya meru-pakan persamaaan atau pertidaksamaan nonlinear.

Salah satu subklas dalam permasalahan pemrograman nonlinear adalah pemrograman kuadratik konveks. Pemrograman kuadratik konveks adalah permasalahan optimisasi berkendala nonlinear dimana fungsi obyektifnya ada-lah fungsi kuadratik konveks, sedangkan kendala-kendalanya merupakan per-samaan atau pertidakper-samaan linear. Fungsi kuadratik konveks pada fungsi ob-yektif yang terdapat dalam pemrograman kuadratik konveks memiliki bentuk

umum dengan G adalah matriks semidefinit positif.

me-thod). Namun dalam skripsi ini metode yang akan dibahas hanya metode

titik-interior primal-dual.

Metode titik-interior primal-dual merupakan salah satu metode nume-rik yang menerapkan metode Newton dalam menyelesaikannya. Pada metode titik-interior primal-dual, pencarian penyelesaian optimum dimulai dari seba-rang titik-interior sehingga akan menghasilkan iterasi yang lebih sedikit kare-na konvergensinya lebih cepat diperoleh.

B. Perumusan Masalah

Berdasarkan uraian yang dikemukakan dalam latar belakang, pokok–

pokok permasalahan yang akan dibahas dalam tulisan ini dapat dirumuskan

sebagai berikut :

1. Apa yang dimaksud dengan pemrograman kuadratik konveks?

2. Apa yang dimaksud dengan metode titik-interior primal-dual untuk

me-nyelesaikan permasalahan optimisasi berkendala pada pemrograman

kua-dratik konveks?

3. Bagaimana cara menyelesaikan pemrograman kuadratik konveks dengan

menggunakan metode titik-interior primal-dual?

4. Bagaimana mengimplementasikan metode titik-interior primal-dual

C. Batasan Masalah

Pembatasan masalah metode titik-interior primal-dual dalam skripsi

ini hanya dibatasi untuk pemrograman kuadratik konveks dengan

kendala-kendala berupa pertidaksamaan.

D. Tujuan Penulisan

Tujuan penulisan skripsi ini adalah untuk menyelesaikan

permasala-han optimisasi berkendala dengan menggunakan metode titik-interior

primal-dual pada pemrograman kuadratik konveks serta bagaimana

mengimplemen-tasikan metode titik-interior primal-dual dengan menggunakan Matlab.

E. Manfaat Penulisan

Manfaat yang diharapkan dalam skripsi ini adalah dapat memahami

bagaimana penggunaan metode titik-interior primal-dual pada pemrograman

kuadratik konveks serta dapat mengimplementasikan metode titik-interior

primal-dual dengan menggunakan Matlab.

F. Metode Penulisan

Metode yang digunakan penulis dalam skripsi ini adalah metode studi

pustaka, yaitu dengan mempelajari buku-buku yang berkaitan dengan topik

G. Sistematika Penulisan

Sistematika penulisan skripsi ini terdiri dari empat bab dengan urutan

sebagai berikut:

BAB I : PENDAHULUAN

Dalam bab ini akan dibahas mengenai latar belakang masalah,

perumusan masalah, batasan masalah, tujuan penulisan,

man-faat penulisan, metode penulisan, dan sistematika penulisan.

BAB II : HIMPUNAN KONVEKS DAN TEORI OPTIMISASI DA-

LAM

Dalam bab ini akan dibahas mengenai matriks dan ruang

vek-tor, fungsi terdiferensial, himpunan konveks dan fungsi

kon-veks, teori optimisasi, dan metode Newton untuk sistem

per-samaan nonlinear yang akan digunakan untuk memahami

me-tode titik-interior primal-dual.

BAB III : METODE TITIK-INTERIOR

Dalam bab ini akan dibahas mengenai pemrograman kuadratik

konveks, metode titik-interior, konsep metode titik-interior

contoh permasalahan pemrograman kuadratik konveks yang

diselesaikan dengan metode titik-interior primal-dual, dan yang

terakhir akan dibahas juga implementasinya dengan

menggu-nakan program Matlab.

BAB IV : PENUTUP

8 BAB II

HIMPUNAN KONVEKS

DAN TEORI OPTIMISASI DALAM

Dalam bab ini akan dibahas mengenai matriks dan ruang vektor, fungsi

terdi-ferensial, himpunan konveks dan fungsi konveks, teori optimisasi, dan metode

Newton untuk sistem persamaan nonlinear yang akan digunakan untuk

memaha-mi metode titik-interior primal-dual.

A. Matriks dan Ruang Vektor

Pada subbab ini akan dibahas mengenai matriks, panjang (norm),

ja-rak, ruang vektor, dan beberapa definisi serta teorema dasar tentang analisis

real.

Definisi 2.1.1 (Ruang Berdimensi n)

Jika n adalah suatu bilangan bulat positif, maka tupel n berurutan adalah suatu

urutan dari n bilangan real , , … , . Himpunan semua tupel n

Definisi 2.1.2 (Matriks)

Matriks adalah jajaran empat persegi panjang dari bilangan-bilangan yang

atur menurut baris dan kolom. Bilangan-bilangan dalam jajaran tersebut

di-sebut dengan elemen dari matriks.

Elemen-elemen yang terletak pada baris i dan kolom j di dalam

ma-triks A dapat dinyatakan sebagai . Sehingga, matriks secara umum dapat

di-tulis sebagai berikut:

Atau lebih singkat dapat ditulis sebagai atau .

Definisi 2.1.3 (Matriks Simetrik)

Sebuah matriks bujur sangkar A adalah simetrik jika dan hanya jika A = AT.

Definisi 2.1.4 (Matriks Definit Positif dan Matriks Semidefinit Positif)

Misalkan A adalah matriks simetrik.

A dikatakan definit positif jika xTAx > 0, , 0.

Dari Definisi 2.1.4, dapat disimpulkan bahwa jika A adalah matriks

definit positif, maka A juga adalah matriks semidefinit positif.

Untuk lebih memahami definisi matriks, matriks simetrik, matriks

de-finit positif dan matriks semidede-finit positif, maka akan diberikan contoh

beri-kut.

Contoh 2.1.1

Misalkan diberikan suatu matriks simetrik:

2 1 0

1 2 1

0 1 2

Untuk mengkaji bahwa matriks A adalah matriks definit positif, maka harus

ditunjukkan bahwa xTAx > 0, , 0.

! ! ! 2_{1 2}1 0₁

0 1 2

! ! !

! ! ! ! " 2!2! ! ! ! " 2!

! #2! ! $ " ! # ! " 2! ! $ " ! # ! " 2! $

2! ! ! ! ! " 2! !%!& !%!&" 2!

2! 2! ! " 2! 2!%!&" 2!

! " #! ! $ " #!% !&$ " !

Dari sini dapat disimpulkan bahwa matriks A bersifat definit positif karena

! " #! ! $ " #!% !&$ " ! ' 0, ,kecuali jika

! ! ! 0.

▄

Contoh 2.1.2

Misalkan diberikan suatu matriks simetrik:

( )2 0_{0 2*}

Untuk mengkaji bahwa matriks G adalah matriks semidefinit positif, maka

ha-rus ditunjukkan bahwa xTGx ≥ 0, .

( ! ! )2 0_{0 2* )}!_! *

! ! ₊2!_{2! ,}

! #2! $ " ! #2! $

2! " 2!

Karena ( 2! " 2! - 0, , maka dapat disimpulkan bahwa

matriks G adalah matriks semidefinit positif.

Definisi 2.1.5 (Ruang Vektor)

Misalkan . adalah himpunan tak kosong yang dilengkapi dengan operasi

pen-jumlahan dan perkalian skalar dengan bilangan real. Artinya, bila diberikan

dua elemen / dan 3 di . dan , 5 , maka penjumlahan / " 3 dan

perka-lian skalar /didefinisikan dan terletak di V juga. Kemudian V dengan kedua

operasi ini disebut ruang vektor jika kedua operasi tersebut memenuhi

aksi-oma-aksioma berikut.

Untuk setiap /, 3, 6 . dan , 5 berlaku:

(i) / " 3 3 " /.

(ii) / " #3 " 6$ #/ " 3$ " 6.

(iii) Ada elemen 7 . sehingga / " 7 /.

(iv) Ada elemen / . sehingga / " # /$ 7.

(v) #/ " 3$ / " 3.

(vi) # " 5$/ / " 5/.

(vii) # 5$/ #5/$.

(viii) 1/ /.

Untuk lebih memahami definisi ruang vektor, maka akan diberikan

Contoh 2.1.3

Buktikan bahwa 8#9 , 9 , … , 9 $|9 , 9 , … , 9 < adalah

ruang vektor!

Bukti:

Misalkan / #9 , 9 , … , 9 $dan3 #= , = , … , = $, maka

/ " 3 #9 " = , 9 " = , … , 9 " = $dan / # 9 , 9 , … , 9 $.

a) / " 3 #9 " = , 9 " = , … , 9 " = $

#= " 9 , = " 9 , … , = " 9 $ 3 " /

b) #/ " 3$ " 6 >#9 " = , 9 " = , … , 9 " = $? " #@ , @ , … , @ $

>#9 , 9 , … , 9 $ " #= , = , … , = $? " #@ , @ , … , @ $

#9 , 9 , … , 9 $ " #= , = , … , = $ " #@ , @ , … , @ $ #9 , 9 , … , 9 $ " ##= , = , … , = $ " #@ , @ , … , @ $$ #9 , 9 , … , 9 $ " #= " @ , = " @ , … , = " @ $ / " #3 " 6$

c) / " 7 #9 , 9 , … , 9 $ " #0, 0, … , 0$

#9 , 9 , … , 9 $ /

d) / " # /$ #9 , 9 , … , 9 $ " # 9 , 9 , … , 9 $

#9 " # 9 $, 9 " # 9 $, … , 9 " # 9 $$ #0, 0, … , 0$

7

e) #/ " 3$ #9 " = , 9 " = , … , 9 " = $

##9 , 9 , … , 9 $ " #= , = , … , = $$ #9 , 9 , … , 9 $ " #= , = , … , = $ / " 3

f) # " 5$/ # " 5$#9 , 9 , … , 9 $

># " 5$9 , # " 5$9 , … , # " 5$9 ?

# 9 " 59 , 9%" 59%, … , 9 " 59 $ # 9 , 9 , … , 9 $ " #59 , 59 , … , 59 $

#9 , 9 , … , 9 $ " 5#9 , 9 , … , 9 $ / " 5/

># 5$9 , # 5$9 , … , # 5$9 ?

# #59 $, #59 $, … , #59 $$ #59 , 59 , … , 59 $

#5/$

h) 1/ 1#9 , 9 , … , 9 $

#19 , 19 , … , 19 $ #9 , 9 , … , 9 $ /

Karena 8#9 , 9 , … , 9 $|9 , 9 , … , 9 < dengan operasi

penjumlahan dan perkalian skalar memenuhi aksioma-aksioma seperti pada

Definisi 2.1.5, maka terbukti bahwa adalah ruang vektor.

▄

Definisi 2.1.6 (Ruang Hasil Kali Dalam)

Hasil kali dalam pada adalah sebuah fungsi yang mengasosiasikan

se-buah bilangan real A , BC dengan sepasang vektor x dan y di , sehingga

ak-sioma-aksioma berikut ini terpenuhi bagi semua vektor x, y, dan z di dan

semua bilangan skalar s.

(i) A , BC AB, C (Aksioma Kesimetrian)

(iii) AE , BC EA , BC (Aksioma Homogenitas)

(iv) A , C - 0 (Aksioma Positivitas)

(v) A , C 0 jika dan hanya jika 0

Sebuah ruang vektor real yang memiliki sebuah hasil kali dalam disebut

ruang hasil kali dalam.

Untuk lebih memahami sifat hasil kali dalam yang pertama, yakni

! H " ! H " … " ! H H ! " H ! " … " H !

H H … H F ! ! !

G

B AB, C

Jadi, terbukti bahwa A , BC AB, C.

▄

Definisi 2.1.7 (Panjang atau Norm)

Panjang atau norm sebuah vektor di dinotasikan dengan L L dan

dide-finisikan sebagai

L L A , CMN # · $MN P! " ! " … " ! .

Sebuah pemetaan L . L dikatakan sebuah norm jika dan hanya jika

memenuhi sifat berikut:

(1) L L - 0,

(2) L L 0 jika dan hanya jika x = 0,

(3) Lα L |R|L L, R ,

Definisi 2.1.8 (Ortogonal)

Dua vektor u dan v di dalam ruang hasil kali dalam di dikatakan

ortogo-nal jika A/, 3C 0.

Teorema 2.1.1 (Hukum Phytagoras)

Jika u dan v adalah vektor-vektor ortogonal di dalam ruang hasil kali dalam di

,maka

L/ " 3L L/L " L3L .

Bukti:

L/ " 3L A/ " 3, / " 3C

A/, /C " A/, 3C " A3, /C " A3, 3C A/, /C " A/, 3C " A/, 3C " A3, 3C

A/, /C " 2A/, 3C " A3, 3C

L/L " L3L

▄

Definisi 2.1.9 (Proyeksi Skalar dan Proyeksi Vektor)

Jika u dan v adalah vektor-vektor di dalam ruang hasil kali dalam di dan

3 0, maka proyeksi skalar dari u pada v diberikan oleh R A/,3C L3L dan

proyeksi vektor dari u pada v diberikan oleh T R U L3L3V

Teorema 2.1.2

Jika 3 0 dan p adalah proyeksi vektordari u pada v, maka / Tdan p

ada-lah ortogonal.

Bukti:

Karena AT, TC A_L3LW 3,_L3LW 3C U_L3LW V A3, 3C R dan A/, TC #A/,3C$_A3,3C R .

Ini mengakibatkan A/ T, TC A/, TC AT, TC R R 0. Oleh karena

itu, / Tdan p adalah ortogonal.

▄

Teorema 2.1.3 (Ketaksamaan Cauchy-Schwarz)

Jika u dan v adalah vektor-vektor di dalam ruang hasil kali dalam di , maka

|A/, 3C| S L/LL3L

Bukti:

Jika 3 0, maka |A/, 3C| 0 L/LL3L. Jika 3 0, maka misalkan p

seba-gai proyeksi vektor dari u pada v. Karena p ortogonal pada / T, maka

me-nurut Hukum Phytagoras

LTL " L/ TL L/L

X LTL L/L L/ TL

X#A/, 3C$_L3L L/L L/ TL

X #A/, 3C$ L/L L3L L/ TL L3L S L/L L3L

Dengan mengambil akarnya, maka diperoleh |A/, 3C| S L/LL3L.

▄

Untuk lebih memahami definisi norm serta sifat-sifat dari norm, maka

akan diberikan contoh berikut.

Contoh 2.1.5

Buktikan bahwa

L L Y|! |

Z

[\

adalah norm!

Bukti:

Untuk membuktikan bahwa L L adalah norm, maka harus ditunjukkan

bah-wa L L memenuhi keempat sifat dari norm.

Misalkan, x dan y adalah sebarang vektor di dan R adalah sebarang

bila-ngan real.

(1) Akan dibuktikan bahwa L L - 0

L L Y|! | Z

[\

- 0

(2) Akan dibuktikan bahwa L L 0 jika dan hanya jika 0.

Jika 0, maka ! 0, ].

Oleh karena itu, ∑ |! |Z_[\ 0 dan L L 0.

Sebaliknya, jika L L 0, maka ∑ |! |Z_[\ 0.

Karena |! | - 0, dengan demikian ∑ |! |Z_[\ 0 hanya dipenuhi jika

|! | 0 sehingga 0.

(3) Akan dibuktikan bahwa LR L |R|L L , R , .

LR L Y|R! |

\

|R| _Y|! | \

`

|R|L L

(4) Akan dibuktikan bahwa L " BL S L L " LBL .

L " BL Y|! " H | \

S Y|! | " \

Y|H | \

L L " LBL

Jadi, L " BL S L L " LBL . ▄

Teorema 2.1.4 (Ketaksamaan Cauchy-Buniakowski-Schwarz)

Misalkan , B , maka

gY ! H \

g S L L LBL

Bukti:

Pertidaksamaan |∑ ! Hh_i\j | S L L LBL akan bersifat trivial jika dan hanya

jika 0 atau B 0. Oleh karena itu, andaikan bahwa dan B, keduanya

taknol. Misalkan, k adalah sebarang bilangan real. Maka,

0 S L " kBL Y#! " kH $ \

Y ! \

" 2k Y ! H " k Y H \ \

L L " 2k Y ! H " k LBL \

Misalkan, LBL , 5 ∑ ! H , dan l L Lh_i\j . Sehingga

jika dan hanya jika diskriminan atau m #25$ 4 l 45 4 l o 0.

Karena itu, 5 o l. Dengan mensubstitusikan nilai dari , 5, dan l, maka

di-peroleh

_Y ! H \

` S L L LBL

Dengan mengambil akarnya, maka diperoleh

gY ! H \

g S L L LBL

▄

Contoh 2.1.6

Buktikan bahwa

L L _Y !

\ `

p

adalah norm!

Bukti:

Untuk membuktikan bahwa L L adalah norm, maka harus ditunjukkan

bah-wa L L memenuhi keempat sifat dari norm.

Misalkan, x dan y adalah sebarang vektor di dan R adalah sebarang

(1) Akan dibuktikan bahwa L L - 0 .

Karena ! - 0 untuk sebarang bilangan real !, maka

L L #Y ! $ / _{- 0} \

(2) Akan dibuktikan bahwa L L 0 jika dan hanya jika 0.

Jika 0, maka ! 0, ].

Oleh karena itu, ∑ !h_i\j 0 dan L L 0.

Sebaliknya, jika L L 0, maka ∑ !h_i\j 0.

Karena ! - 0, dengan demikian #∑ ! $h_i\j / 0 hanya dipenuhi

jika ! 0 sehingga 0.

(3) Akan dibuktikan bahwa LR L |R|L L , R , .

LR L _Y#R! $

\

`

_R Y ! \

` /

|R| _Y ! \

` /

(4) Akan dibuktikan bahwa L " BL S L L " LBL .

L " BL

Y#! " H $ \

Y ! " 2 \

Y ! H " Y H \ \

S L L " 2 gY ! H \

g " LBL #Sifat nilai mutlak$

S L L " 2L L LBL " LBL # Ketaksamaan

Cauchy-Buniakowski-Schwarz)

#L L " LBL $

Dengan mengambil akarnya, maka diperoleh

L " BL S L L " LBL .

▄

Selanjutnya, akan diberikan definisi dan sifat jarak pada .

Definisi 2.1.10 (Jarak)

Jarak antara dua buah titik titik dan Bdinotasikandengan

Oleh karena itu, ∑ #! H $_\ 0 dan L BL 0.

Sebaliknya, jika L BL 0, maka ∑ #! H $_\ 0.

Karena #! H $ - 0, dengan demikian ∑ #!_\ H $ 0 hanya dipe-

nuhi jika ! H 0 sehingga B.

▄

(3) Akan dibuktikan bahwa L DL S L BL " LB DL.

Bukti:

L DL L B " B DL

A B " B D, B " B DC

A B, B " B DC " AB D, B " B DC A B, BC " A B, B DC " AB D, BC

"AB D, B DC

L BL " A B, B DC " AB D, BC " LB DL

L BL " A B, B DC " A B, B DC " LB DL L BL " 2A B, B DC " LB DL

S L BL " 2L BLLB DL " LB DL (Ketaksamaan

Cauchy-Schwarz)

#L BL " LB DL$

L DL S L BL " LB DL.

Jadi, terbukti untuk L DL S L BL " LB DL.

▄

(4) Akan dibuktikan bahwa L BL LB L.

Bukti:

L BL L# 1$#B $L

| 1|LB L

LB L

▄

Teorema 2.1.6 (Hukum Paralelogram)

Untuk semua , B

L " BL " L BL 2#L L " LBL $

Bukti:

L " BL " L BL

A " B, " BC " A B, BC

A , " BC " AB, " BC " A , BC AB, BC

A , C " AB, BC " A , C " AB, BC 2A , C " 2AB, BC

2L L " 2LBL 2#L L " LBL $

▄

Selanjutnya, akan diberikan definisi kitar dan titik-interior.

Definisi 2.1.11 (Kitar)

Diberikan titik dan δ > 0. Kitar- δ dari x didefinisikan sebagai

st# $ 8B |LB L o δ<

Definisi 2.1.12 (Titik Interior)

Misalkan m v dan m. Titik x dikatakan titik interior dari D

jika ada suatu kitar- δ dari x sedemikian sehingga s_t# $ v m.

Untuk lebih memahami definisi titik interior, maka akan diberikan

contoh berikut.

Contoh 2.1.7

Himpunan ini merepresentasikan titik yang berada di dalam lingkaran dengan

pusat (0,0) dan radius 1 seperti pada Gambar 2.1.1.

Gambar 2.1.1 Lingkaran ! " ! o 1

Titik-titik yang berada di dalam lingkaran adalah titik interior. Sedangkan,

ti-tik-titik yang berada pada batas dan luar lingkaran bukan merupakan titik

inte-rior.

Definisi 2.1.13 (Himpunan Terbuka)

Himpunan semua titik interior dari D disebut interior D dan dinotasikan

de-ngan int(D). Selanjutnya, jika int(D) = D, yakni setiap titik dari D adalah titik

interior dari D, maka D adalah himpunan terbuka.

Definisi 2.1.14 (Himpunan Tertutup)

Suatu himpunan m v dikatakan tertutup jika dan hanya jika

Untuk lebih memahami definisi himpunan terbuka, maka akan

diberi-kan contoh berikut.

Contoh 2.1.8

Berdasarkan Contoh 2.1.7, A adalah himpunan terbuka, karena titik-titik yang

berada di dalam lingkaran adalah titik interior.

Selanjutnya, akan diberikan definisi relasi dan himpunan terurut secara

parsial.

Definisi 2.1.15 (Relasi)

Sebuah relasi dari suatu himpunan A ke himpunan B adalah suatu subset R

dari X x, di mana X x 8# , 5$: , 5 x<.

Relasi dapat pula ditulis sebagai z 5 yang berarti bahwa # , 5$ z.

Definisi 2.1.16 (Himpunan Terurut Secara Parsial)

Misalkan R adalah sebuah relasi pada sebuah himpunan S, maka R disebut

re-lasi urutan parsial jikayang memenuhi tiga sifat berikut:

(i) Refleksif

(ii) Antisimetris

R dikatakan antisimetris jika dan hanya jika z 5 dan 5 z , maka

5, untuk setiap # , 5$ {.

(iii) Transitif

R dikatakan transitif jika dan hanya jika z 5 dan 5 z l, maka z l,

untuk setiap # , 5, l$ {.

Himpunan S bersama dengan suatu relasi urutan parsial R pada A dikatakan

himpunan terurut secara parsial.

Relasi urutan parsial dari sebuah himpunan S biasanya dinotasikan

dengan S atau -. Relasi S 5 dibaca dengan “a mendahului b”, sedangkan

relasi - b dibaca dengan “a melampaui b”.

Untuk lebih memahami definisi himpunan terurut secara parsial, maka

akan diberikan contoh berikut.

Contoh 2.1.9

Perhatikan bilangan bulat positif }. Didefinisikan relasi " membagi 5"

de-ngan |5, jika terdapat sebuah l } sedemikian sehingga l 5. Misalnya,

2|4, 3|12, 7|21, dan seterusnya. Tunjukkan bahwa pembagian adalah sebuah

a. Refleksif: | .

b. Antisimetris: Jika |5 dan 5| maka 5.

c. Transitif: Jika |5 dan 5|l maka |l.

Bukti:

a. Karena · 1 , maka | .

b. Andaikan |5 dan 5| , misalkan 5 † dan E5. Maka, 5 †E5

se-hingga †E 1. Karena † dan E adalah bilangan bulat positif, maka

† 1 dan E 1. Dengan demikian, 5.

c. Andaikan |5 dan 5|l, misalkan 5 † dan l E5. Maka, l E†

se-hingga |l.

▄

Berikut ini diberikan definisi batas atas, supremum, batas bawah, dan

infimum.

Definisi 2.1.17 (Batas Atas)

Misalkan A adalah himpunan bagian dari sebuah himpunan S yang terurut

Sebuah elemen M dalam S dikatakan sebuah batas atas dari A jika M

me-lampaui setiap elemen dari A, yaitu M adalah sebuah batas atas dari A jika

un-tuk setiap x dalam A diperoleh ! S ‡.

Definisi 2.1.18 (Supremum)

Jika sebuah batas atas dari A mendahului setiap batas atas lain dari A maka

di-sebut batas atas terkecil atau supremum dari A yang dinotasikan dengan

sup (A).

Definisi 2.1.19 (Batas Bawah)

Sebuah elemen m dalam S dikatakan sebuah batas bawah dari A jika m

men-dahului setiap elemen dari A, yaitu m adalah sebuah batas bawah dari A jika

untuk setiap x dalam A diperoleh ˆ S !.

Definisi 2.1.20 (Infimum)

Jika sebuah batas bawah dari A melampaui setiap batas bawah lain dari A

ma-ka disebut batas bawah terbesar atau infimum dari A yang dinotasikan

dengan inf (A).

Definisi 2.1.21 (Terbatas ke Atas dan Terbatas ke Bawah)

a. Himpunan { dikatakan terbatas ke atas jika ada bilangan 9

sedemi-kian sehingga E S 9 untuk semua E {. Setiap bilangan 9 dikatakan batas

atas dari {.

b. Himpunan { dikatakan terbatas ke bawah jika ada bilangan @

se-demikian sehingga @ S E untuk semua E {. Setiap bilangan @

dikata-kan batas bawah dari {.

Lemma 2.1.1

Batas bawah ‰ dari himpunan tak kosong { di adalah infimum dari { jika

dan hanya jika Š ' 0 terdapat ! { sedemikian sehingga ‰ " Š ' !.

Bukti

#‹$

Diketahui ‰ inf { dan Š ' 0.

Akan ditunjukkan terdapat ! { sedemikian sehingga ‰ " Š ' !.

Jika 5 batas bawah { maka 5 S ‰.

Karena ‰ " Š ' ‰ maka ‰ " Š bukan batas bawah {.

Karena ‰ " Š bukan batas bawah { maka harus ada ! { sehingga ‰ " Š ' !.

#Œ$

Jika ‰ suatu batas bawah {, dan untuk setiap Š ' 0 terdapat ! { sedemikian

Akan dibuktikan ‰ inf {.

Misalkan bahwa 5 suatu batas bawah {. Karena ! { dan 5 suatu batas

ba-wah { maka ! - 5.

Karena ‰ " Š ' ! maka ‰ " Š ' 5.

Jadi untuk setiap Š ' 0 berlaku ‰ " Š ' 5. Andaikan 5 ' ‰ maka jika diambil

Š •Ž• akan diperoleh ‰ " Š ••• sehingga 5 ' ‰ " Š ' ‰ dan 5 ' ‰ " Š ' !

yang kontradiksi dengan pernyataan bahwa 5 batas bawah. Jadi, jika 5 batas

bawah { haruslah ‰ - 5 sehingga ‰ merupakan batas bawah terbesar atau

‰ inf {.

▄

Definisi 2.1.22 (Barisan Naik dan Barisan Turun)

Misalkan ‘ 8! < merupakan barisan bilangan real. Barisan ‘ dikatakan

naik jika memenuhi pertidaksamaan

! S ! S S ! S ! • S

dan dikatakan turun jika memenuhi pertidaksamaan

! - ! - - ! - ! •

-Jika barisan ‘ merupakan barisan naik atau barisan turun maka merupakan

Teorema 2.1.7

Barisan turun dan terbatas ke bawah adalah konvergen.

Bukti:

Diberikan 8! < turun dan terbatas ke bawah. Karena 8! : ’ }< “ maka

terdapat 5 dan 5 inf8! : ’ }<. Jadi, untuk setiap ’ } berlaku

! - 5 (2.1)

Karena 5 inf8! : ’ }<, maka untuk Š ' 0 yang diberikan terdapat s }

dan

5 Š ' !_” - 5 (2.2) Karena 8! < turun, maka mengingat (2.1) dan (2.2), untuk setiap ’ - s

ber-laku

5 Š ' !_” - ! - 5 ' 5 " Š (2.3) Jadi, diperoleh pernyataan bahwa untuk setiap Š ' 0 terdapat s }

sedemi-kian sehingga untuk setiap ’ - } dan ’ - s, maka |! 5| o Š. Jadi, 8! <

konvergen dan lim ! 5 inf8! : ’ }<.

▄

Untuk lebih memahami definisi batas atas, batas bawah, supremum,

Contoh 2.1.10

Misalkan . 8 , 5, l, r, •, –, —< terurut seperti pada Gambar 2.1.1 dan

misal-kan ‘ 8l, r, •<. Tentukan batas atas, batas bawah, supremum, dan infimum

dari X!

– — • l r

5

Gambar 2.1.2 Himpunan Terurut

Penyelesaian:

Elemen •, –, dan — didahului oleh setiap elemen dari X, sehingga •, –, dan —

adalah batas atas dari X.

Elemen mendahului setiap elemen dari X, sehingga adalah batas bawah

dari X.

Elemen • mendahului – dan —, sehingga • adalah supremum dari X.

Elemen mendahului setiap batas bawah dari X, sehingga adalah infimum

dari X.

Definisi 2.1.23 (Barisan Cauchy)

Barisan 8 _˜< v dikatakan Barisan Cauchy jika lim _,•™šL _•L 0.

Dengan kata lain untuk setiap Š ' 0, terdapat bilangan bulat s sedemikian

sehingga L _•L o Š untuk semua ˆ, ‰ ' s.

Untuk lebih memahami definisi barisan Cauchy, maka akan diberikan

contoh berikut.

Contoh 2.1.11

Buktikan bahwa › œ adalah barisan Cauchy!

Bukti:

Jika diberikan Š ' 0, dapat dipilih s } sedemikian sehingga s '

• . Maka,

jika ’, ˆ - s, diperoleh S ”o

•

dan dengan cara yang sama diperoleh

S_”o• . Oleh karena itu, jika ’, ˆ - s, maka

ž ž S " o•"• Š.

Karena berlaku untuk sebarang Š ' 0, maka dapat disimpulkan bahwa › œ

adalah barisan Cauchy.

Definisi 2.1.24 (Konvergen)

Barisan 8E < dikatakan konvergen jika terdapat E dengan sifat, untuk

se-barang Š ' 0 yang diberikan, terdapat s } sehingga untuk semua ’ }

dengan ’ - s berlaku |E E | o Š. Bilangan s dinamakan limit 8E < untuk

’ ™ ∞ dan ditulis lim_’™∞E_’ EataudisingkatlimE E.

Untuk lebih memahami definisi konvergen dari suatu barisan, maka

akan diberikan contoh berikut.

Contoh 2.1.12

Jika E l untuk semua ’ } dan c suatu konstanta, maka buktikan bahwa

8E < konvergen ke c!

Bukti:

Untuk semua ’ } berlaku |E l| 0. Jadi, jika diberikan Š ' 0, maka

terdapat s } sehingga ’ - s berlaku |E l| o Š. Dalam hal ini, dapat

diambil bilangan bulat positif manapun untuk }, karena |E l| 0 o Š

un-tuk ’ }.

▄

B. Fungsi Terdiferensial

Pada subbab ini akan dibahas mengenai fungsi, fungsi kontinu, fungsi

terdiferensial secara kontinu, fungsi terdiferensial dua kali secara kontinu dan

beberapa definisi serta teorema dasar tentang kalkulus.

Definisi 2.2.1 (Fungsi atau Pemetaan)

Relasi dari himpunan A ke himpunan B disebut dengan fungsi atau pemetaan,

jika dan hanya jika setiap anggota dari himpunan A berpasangan tepat hanya

dengan sebuah anggota dalam himpunan B.

Fungsi f dapat pula dinotasikan dengan f :A→ B, yang mana

me-nunjukkan bahwa fungsi tersebut merupakan pemetaan dari himpunan A ke

himpunan B. Himpunan A disebut dengan domain atau daerah asal, sedangkan

himpunan B disebut dengan kodomain atau daerah kawan.

Definisi 2.2.2 (Fungsi Kontinu di )

Misalkan , –: ™ , dan l .Fungsi f dikatakan kontinu di c, jika

untuk setiap Š ' 0 yang diberikan, dapat dicari ¡ ' 0, sehingga untuk semua

Teorema 2.2.1

Jika –, — kontinu di x, maka – — juga kontinu di x.

Bukti:

Andaikan f dan — kontinu di x.

Akan dibuktikan bahwa – — kontinu di x.

Jika Š adalah sebarang bilangan positif yang diberikan, maka Š/2 adalah

posi-tif. Karena f kontinu di x, maka untuk setiap Š • ' 0, terdapat suatu

bila-ngan positif ¡ , sedemikian sehingga untuk H dan |! H| o ¡ maka |–#!$ –#H$| o Š dan karena — kontinu di x, maka untuk setiap

Š • ' 0, terdapat suatu bilangan positif ¡ , sedemikian sehingga untuk

H dan |! H| o¡ maka |—#!$ —#H$| o Š . Ambil sebarang Š ' 0

dan pilih ¡ min 8 ¡ , ¡ <, yakni pilih ¡ yang terkecil diantara ¡ dan ¡ .

Maka, untuk H dan |! H| o¡ mengimplikasikan | –#!$ –#H$ —#!$ —#H$ |

| –#!$ –#H$ " # 1$ —#!$ —#H$ |

S |–#!$ –#H$| " |# 1$ —#!$ —#H$ | (Ketaksamaan Segitiga) S |–#!$ –#H$| " |# 1$|| —#!$ —#H$ |

S |–#!$ –#H$| " |—#!$ —#H$|

Langkah-langkah di atas memperlihatkan bahwa untuk H dan |! H| o ¡, maka | –#!$ –#H$ —#!$ —#H$ | o Š.

Oleh karena itu, dapat disimpulkan bahwa – — kontinu di x.

▄

Definisi 2.2.3 (Nilai Maksimum, Nilai Minimum, dan Nilai Ekstrim)

Andaikan S adalah daerah asal dari f yang memuat titik c. Dapat dikatakan

bahwa:

(i) f(c) adalah nilai maksimumf pada S jika –#l$ - –#!$ untuk semua

x di S.

(ii) f(c) adalah nilai minimum f pada S jika –#l$ S –#!$ untuk semua x

di S.

(iii) f(c) adalah nilai ekstrim f pada S jika f(c) adalah nilai maksimum

atau nilai minimum.

Teorema 2.2.2 (Titik Kritis)

Andaikan f terdefinisikan pada selang , 5 yang memuat titik c. Jika f(c)

adalah nilai ekstrim, maka c haruslah berupa suatu titik kritis, yakni c berupa

salah satu:

(i) Titik ujung dari , 5 .

(iii) Titik singular dari f, yakni titik c sedemikian sehingga –¢#l$ tidak ada.

Bukti:

Akan dibuktikan untuk f(c) yang berupa nilai maksimum f pada , 5 .

Andaikan bahwa c bukan titik ujung ataupun titik singular, sehingga harus

di-perlihatkan bahwa c adalah titik stasioner. Karena f(c) adalah nilai maksimum,

maka –#!$ S –#l$ untuk semua x dalam , 5 diperoleh –#!$ –#l$ S 0.

Jadi, jika ! o l sehingga ! l o 0, maka £#¤$Ž£#¥$

¤Ž¥ - 0. Sedangkan, jika ! ' l, maka £#¤$Ž£#¥$

¤Ž¥ S 0. Akan tetapi, –¢#l$ ada, karena c bukan titik singu-lar. Karena f terdiferensial pada c, maka diperoleh –¢#l$ –_Ž¢#l$ lim¤™¥¦£#¤$Ž£#¥$

¤Ž¥ - 0 dan –¢#l$ –•¢#l$ lim¤™¥§

£#¤$Ž£#¥$

¤Ž¥ S 0, yang ma-na mengakibatkan bahwa –¢#l$ - 0 dan –¢#l$ S 0. Sehingga dapat disimpul-kan bahwa –¢#l$ 0, yang mana menunjukkan bahwa c adalah titik stasio-ner. Jadi, terbukti untuk f(c) yang berupa nilai maksimum f pada , 5 .

Se-lanjutnya, untuk f(c) yang berupa nilai minimum f pada , 5 dibuktikan

dengan cara yang sama seperti untuk f(c) yang berupa nilai maksimum f pada

, 5 .

Teorema 2.2.3 (Teorema Nilai Rata-Rata)

Jika – kontinu pada selang tertutup , 5 dan terdiferensiasikan pada

titik-titik dalam dari # , 5$, maka terdapat paling sedikit satu bilangan c dalam

# , 5$ dengan

–#5$ –# $

5 –¢#l$ #2.4$

atau sama dengan –#5$ –# $ –¢#l$#5 $.

Bukti:

Pembuktian ini berdasarkan pada analisis dari fungsi E#!$ –#!$ —#!$

yang diperlihatkan pada Gambar 2.2.1.

Gambar 2.2.1 Teorema Nilai Rata-Rata.

Pada Gambar 2.2.1, terlihat bahwa H —#!$ adalah persamaan garis yang

–#5$ –# $ /#5 $ dan melalui titik # , –# $$, maka garis tersebut

me-miliki persamaan titik kemiringan, yakni

—#!$ –# $ –#5$ –# $₅ #! $

X —#!$ –# $ "–#5$ –# $₅ #! $ #2.5$

Sedangkan, jarak antara fungsi – dengan fungsi — adalah

E#!$ –#!$ —#!$

Sehingga persamaan (2.5) dapat ditulis menjadi

E#!$ –#!$ —#!$

–#!$ –# $ –#5$ –# $₅ #! $ #2.6$

Dapat dilihat bahwa E#5$ E# $ 0 dan bahwa untuk ! dalam # , 5$

berla-ku

E¢_{#!$ –}¢_#!$ –#5$ –# $

5 #2.7$

Jika diketahui bahwa terdapat suatu bilangan c dalam # , 5$ yang memenuhi

E¢_{#l$ 0, maka bukti akan selesai. Sehingga, persamaan (2.7) menjadi}

0 –¢_#l$ –#5$ –# $

5 #2.8$

yang mana persamaan (2.7) tidak lain merupakan persamaan (2.4).

Untuk melihat bahwa E¢#l$ 0 untuk suatu c dalam # , 5$ alasannya jelas karena s kontinu pada , 5 yang merupakan selisih dua fungsi kontinu.

men-capai nilai maksimum dan minimum, sehingga s harus mencapai nilai

maksi-mum ataupun nilai minimaksi-mum pada , 5 . Jika kedua nilai ini kebetulan adalah

0, maka E#!$ secara identik adalah 0 pada , 5 , akibatnya E¢#!$ 0 untuk semua x dalam # , 5$. Jika nilai maksimum atau nilai minimum berlainan

de-ngan 0, maka nilai tersebut dicapai pada sebuah titik-dalam c, karena E# $

E#5$ 0. Sekarang s mempunyai turunan di setiap titik dari # , 5$, sehingga

berdasarkan Teorema Titik Kritis diperoleh E¢#l$ 0. ▄

Definisi 2.2.4 (Fungsi Kontinu di )

Sebuah fungsi –: ™ dikatakan kontinu pada « , jika untuk setiap

, 0

>

ε terdapat δ >0 sedemikian sehingga L «L o δ maka

L–# $ –#«$L o Š .

Definisi 2.2.5 (Turunan Parsial)

Andaikan bahwa f adalah suatu fungsi dua variabel dari ! dan H.

Turunan parsial f terhadap ¬ adalah fungsi yang dinyatakan dengan

–¤#!, H$ atau -£#¤,®$_-¤ yang nilainya di setiap titik #!, H$ diberikan oleh

apabila limitnya ada. Dengan cara yang sama, turunan parsial f terhadap ²,

fungsi yang dinyatakan dengan –_®#!, H$ atau -£#¤,®$

-® yang nilainya di setiap ti-tik #!, H$ diberikan oleh

–®#!, H$ ¯–#!, H$_{¯H ∆®™±}lim –#!, H " ∆H$ –#!, H$_∆H

apabila limitnya ada.

Untuk lebih memahami definisi turunan parsial, maka akan diberikan

contoh berikut.

Contoh 2.2.1:

Tentukan turunan parsial terhadap x dan turunan parsial terhadap y dari fungsi

yang dinotasikan dengan –#!, H$ ! H " 5! " 4!

Penyelesaian:

¯–#!, H$

¯H ∆¤™±lim

–#! " ∆!, H$ –#!, H$ ∆!

lim ∆¤™±

#! " ∆!$ H " 5#! " ∆!$ " 4 #! H " 5! " 4$ ∆!

lim ∆¤™±

! H " 2!∆!H " #∆!$ H " 5! " 5∆! " 4 #! H " 5! " 4$ ∆!

lim ∆¤™±

2!H " 5

Definisi 2.2.6 (Fungsi Terdiferensial Kontinu)

Sebuah fungsi kontinu –: ™ dikatakan terdiferensial kontinu di

Definisi 2.2.8 (Turunan Berarah)

Fungsi –: ™ terdiferensial kontinu pada himpunan terbuka D⊆ .

Maka untuk x∈D dan ¼ turunan berarah dari f di dalam arah d

di-definisikan sebagai

–¢_{# , ¼$ ½ lim} ¾™±

–# " ¿¼$ –# $

¿ ³–# $ ¼

dimana ³–# $ adalah gradien dari f di x, vektor berukuran n x 1.

Teorema 2.2.4 (Teorema Taylor di )

Misalkan –: ™ terdiferensial secara kontinu dan bahwa ¼ . Maka

diperoleh

–# " ¼$ –# $ " ³–# " À¼$ ¼ (2.9)

untuk suatu À #0,1$.

Bukti:

Misalkan –: ™ terdiferensial secara kontinu pada himpunan terbuka

m v sehingga m dan ¼ . Dengan menggunakan Definisi Turunan

Berarah diperoleh bahwa

–¢_{# , ¼$ lim} ¾™±

–# " ¿¼$ –# $

¿ ³–# $ ¼ #2.10$

Misalkan, f(x) merupakan fungsi norm ‰ , yakni f(x) = L L .

Jadi, turunan berarah dari fungsi f(x) ada untuk sebarang x dan d.

Misalkan f terdiferensial secara kontinu pada suatu kitar dari x, maka

dipero-leh

–¢_{#–# $, ¼$ ³–# $ ¼ (2.11)}

Untuk membuktikan rumus ini, didefinisikan fungsi

“#À$ –# " À¼$ –#B#À$$

dimana B#À$ " À¼. Dapat dicatat bahwa

lim ¾™±

–# " ¿¼$ –# $

¿ ¾™±lim

“#¿$ “#0$

¿ “¢#0$

Dengan menggunakan aturan rantai pada –#B#À$$ diperoleh

“¢_#À$ ¯–>B#À$?

¯B · ¯B¯À "¯–>B#À$?¯B · ¯B¯À " … "¯–>B#À$?¯B · ¯B¯À " … " ¯–#B#À$$

¯B ·¯B¯À

Y¯–>B#À$?_¯B · ³B \

#À$

Y¯–>B#À$?_¯B · r \

³–>B#À$? ¼

³–# " À¼$ ¼ (2.12)

Substitusikan untuk À 0 ke dalam persamaan (2.12), sehingga diperoleh

yang mana persamaan (2.13) adalah persamaan (2.11).

Berdasarkan Teorema Nilai Rata-Rata, misalkan diberikan sebuah fungsi yang

terdiferensial secara kontinu “: ™ dan terdapat dua bilangan real

À± dan À yang memenuhi À ' À± untuk suatu Ä #À±, À $, sehingga

dipero-leh

“#À $ “#À±$ " “¢#Ä$#À À±$ (2.14)

Dapat diingat bahwa “#À$ –# " À¼$. Andaikan bahwa À_± 0 dan À 1. Jika À diganti menjadi À , maka diperoleh

“#À $ –# " À ¼$ (2.15)

Substitusikan À 1 ke dalam persamaan (2.15) sehingga diperoleh

“#1$ –# " ¼$. Jika À diganti menjadi À_±, maka

“#À±$ –# " À±¼$ (2.16)

Substitusikan À_± 0 ke dalam persamaan (2.16) sehingga diperoleh

“#0$ –# $. Suatu perluasan dari hasil ini untuk fungsi multivariabel –: ™ bahwa untuk sebarang vektor d diperoleh bahwa

–# " ¼$ –# $ " ³–# " À¼$ ¼untuk suatu À #0,1$.

▄

Definisi 2.2.9 (Fungsi Terdiferensial Dua Kali Secara Kontinu)

dua kali secara kontinu di jika _

(x) ada dan kontinu dengan

] 1, … , ’ dan Å 1, … , ’.

Definisi 2.2.10 (Matriks Hesse)

Misalkan –: ™ dan , matriks Hesse dari f didefinisikan sebagai

matriks simetri berukuran n x n, yang dinotasikan dengan H(x) dengan

ele-men-elemen sebagai berikut:

³ –# $ _{¯! ¯! # $, ] 1, … , ’ dan Å 1, … , ’}¯ –

Atau dapat juga dinyatakan sebagai berikut:

Æ# $

Untuk lebih memahami definisi gradien dan matriks Hesse, maka akan

diberikan contoh berikut.

Contoh 2.2.2:

Maka ³Í#! , ! $ F -Î

-¤M#! , ! $

-Î

-¤N#! , ! $

G +2_2!! 2₅, dan

Æ#! , ! $

-N_Î#¤M,¤N$

-¤MN

-N_Î#¤M,¤N$

-¤M-¤N

-NÎ#¤M,¤N$

-¤N-¤M

-NÎ#¤M,¤N$

-¤NN

)2 0_{0 2*} .

C. Himpunan Konveks dan Fungsi Konveks

Pada subbab ini akan dibahas mengenai himpunan konveks dan fungsi

konveks serta beberapa teorema-teorema yang berkaitan dengan fungsi

kon-veks.

Definisi 2.3.1 (Himpunan Konveks)

Sebuah himpunan Ï v disebut himpunan konveks apabila memenuhi

si-fat berikut: jika diberikan sebarang dua titik x1, x2∈C, maka

θx1 +(1−θ) x2 ∈C _{untuk setiap} θ∈

[ ]

0,1 . Suku θx1+(1−θ) x2 dengan

[ ]

0,1 ∈

θ menggambarkan titik-titik yang terletak pada ruas garis yang

meng-hubungkan x1 dan x2.

Dalam pengertian geometri, himpunan konveks dapat digambarkan

Gambar 2.3.1 Ilustrasi dari Himpunan Konveks.

Berdasarkan Gambar 2.3.1, jika diberikan sebarang dua titik x1 dan x2

yang berada di dalam C, maka ruas garis yang menghubungkan titik x1 dan x2

akan berada di dalam C.

Untuk lebih memahami definisi himpunan konveks, maka akan

diberi-kan contoh berikut.

Contoh 2.3.1:

(

)

{

₁, ₂ : ₁2 + ₂2 <1

}

= x x x x

K v

Himpunan ini merepresentasikan titik yang berada di dalam lingkaran dengan

Gambar 2.3.2 Lingkaran x2 + y2 =1

Berdasarkan Gambar 2.3.2, jika diberikan sebarang dua titik x1 dan x2

yang berada di dalam lingkaran, maka ruas garis yang menghubungkan titik x1

dan x2 akan berada di dalam lingkaran.

Definisi 2.3.2 (Fungsi Konveks)

Fungsi –: ™ _dikatakan konveks jika untuk dua vektor x1, x2

ber-laku f(θ x1+(1−θ) x2)≤θ f (x1) +(1−θ) f (x2) untuk semua θ∈

[ ]

0,1 .

Fungsi f dikatakan konveks tegas (strictly convex) jika

θ

(

f x1+(1−θ) x2)<θ f (x1) +(1−θ)f (x2) dimana x1≠x2 dan 0 <θ< 1.

Gambar 2.3.3 Contoh Fungsi Konveks.

Gambar 2.3.3 adalah fungsi konveks, dimana θ f (x1) +(1−θ) f (x2)

digambarkan sebagai titik pada tali busur yang menghubungkan f (x1) dan

f (x2), sedangkan f(θ x1+(1−θ) x2) adalah titik pada f yang

menghubung-kan f(x1) dan f(x2). Berdasarkan Gambar 2.3.3, dapat dilihat bahwa ¿–# $ "

f

) 1

( −θ # $ berada di atas –#¿ " #1 ¿$ $. Jadi, –#¿ "

#1 ¿$ $ S ¿–# $ " (1−θ) f # $, yang berarti f konveks.

Untuk lebih memahami definisi fungsi konveks, maka akan diberikan

contoh berikut.

Contoh 2.3.2:

2H 5¿! " 5¿H 5H " 7.25

Sedangkan,

¿Í# $ " #1 ¿$Í#B$ ¿#! " ! 2! 5! $ " #1 ¿$

#H " H 2H 5H $ " 7.25

¿! " ¿! 2¿! 5¿! " H " H 2H 5H ¿H ¿H " 2¿H " 5¿H " 7.25

Karena θ∈

[ ]

0,1 , maka θ2 <θ

sehingga diperoleh:

Í#¿ " #1 ¿$B$

#¿ #! 2! H " H $ " 2¿! H 2¿H " H $

"#¿ #! 2! H " H $ " 2¿! H 2¿H " H $ 2¿! " 2¿H 2H 5¿! " 5¿H 5H " 7.25

o #¿#! 2! H " H $ " 2¿! H 2¿H " H $

"#¿#! 2! H " H $ " 2¿! H 2¿H " H $ 2¿! " 2¿H 2H 5¿! " 5¿H 5H " 7.25

o ¿! 2¿! H " ¿H " 2¿! H 2¿H " H " ¿! 2¿! H

"¿H " 2¿! H 2¿H " H 2¿! " 2¿H 2H 5¿!

"5¿H 5H " 7.25

¿! " ¿! 2¿! 5¿! " H " H 2H 5H ¿H ¿H

Jadi, Í#¿ " #1 ¿$B$ S ¿Í# $ " #1 ¿$Í#B$ untuk sebarang θ∈

[ ]

0,1 ,

maka terbukti bahwa Í# $ ! " ! 2! 5! " 7.25 dengan

adalah fungsi konveks.

▄

Teorema 2.3.1

Misalkan S ⊆ adalah himpunan konveks terbuka tidak kosong dan

–: { ™ adalah fungsi terdiferensial. Maka f dikatakan konveks jika

dan hanya jika

–# $ - –#«$ " ³–#«$ # «$, «, {

Bukti:

) (⇒

Misalkan f konveks.

Akan ditunjukkan bahwa –# $ - –#«$ " ³–#«$ # «$, «, {.

Berdasarkan Definisi Fungsi Konveks bahwa jika f adalah konveks, maka

un-tuk semua ¿ dengan 0 < ¿ < 1 berlaku

–#¿ " #1 ¿$«$ S ¿–# $ " #1 ¿$–#«$ Ð –#¿ " « ¿«$ S ¿–# $ " –#«$ ¿–#«$

Ð –#« " ¿# «$$ S ¿>–# $ –#«$? " –#«$

Ð –#« " ¿# _¿ «$$ –#«$S –# $ –#«$

Dengan pengambilan limit untuk ™ 0 , maka

lim ¾™±

–#« " ¿# «$$ –#«$

¿ S –# $ –#«$

Berdasarkan Definisi Turunan Berarah diperoleh

³–#«$ # «$S –# $ –#«$

Maka terbukti bahwa

–# $ - –#«$ " ³–#«$ # «$

) (⇐

Misalkan bahwa –# $ - –#«$ " ³–#«$ # «$.

Akan ditunjukkan f konveks.

Anggap bahwa –# $ - –#«$ " ³–#«$ # «$, «, { benar.

Pilih sebarang x1, x2 { dan ¿ " #1 ¿$ untuk semua ¿ #0,1$.

Maka diperoleh

–# $ - –#«$ " ³–#«$ # «$

dan

–# $ - –#«$ " ³–#«$ # «$

Oleh karena itu,

¿–# $ " #1 ¿$–# $

¿–#«$" ³–#«$ ¿# «$ "–#«$" ³–#«$ # «$ ¿–#«$

³–#«$ ¿# «$

–#«$" ³–#«$ #¿# «$ " # «$ ¿# «$$

–#«$" ³–#«$ #¿ ¿«" « ¿ "¿«$ –#«$" ³–#«$ #¿ " #1 ¿$ «$

–#¿ " #1 ¿$ $

Karena –#¿ " #1 ¿$ $ S ¿–# $ " #1 ¿$–# $ untuk sebarang

x1, x2 { dan ¿ #0,1$, maka terbukti bahwa – konveks.

▄

Teorema 2.3.2

Misalkan { v adalah himpunan konveks terbuka tidak kosong dan

–: { v ™ terdiferensial dua kali secara kontinu. Maka f adalah konveks

jika dan hanya jika matriks Hesse adalah semidefinit positif pada setiap titik

dalam S.

Bukti:

#Ñ$

Andaikan bahwa matriks Hesse ³ –# $ adalah semidefinit positif pada setiap

titik {. Akan dibuktikan bahwa f adalah konveks. Anggap , « {.

# «$ ³ –#Ò$# «$ dimana Ò « " ¿# «$, ¿ #0,1$. Dapat dicatat

bahwa Ò {. Karena ³ –# $ adalah semidefinit positif, {, maka

# «$ ³ –#Ò$# «$ - 0. Sehingga diperoleh –# $ - –#«$ "

³–#«$ # «$. Dengan menggunakan Teorema 2.3.1 diperoleh bahwa f

ada-lah fungsi konveks.

#Ó$

Andaikan bahwa f adalah fungsi konveks dan « {.

Akan dibuktikan bahwa T ³ –#«$T - 0, Ô . Karena S terbuka, maka

terdapat ¡ ' 0 sedemikian sehingga ketika |k| o ¡, « " kT {. Dengan

Teo-rema 2.3.1 diperoleh

–#« " kT$ - –#«$ " ³–#«$ #« " kT «$

X –#« " kT$ - –#«$ " k³–#«$ T (2.17)

Karena –# $terdiferensial dua kali pada «, maka

–#« " kT$ –#«$ " ³–#«$ #« " kT «$ "1_{2 #« " kT «$} ³ –#«$

#« " kT «$ " Õ#LkTL $

–#«$ " k³–#«$ T "1_{2 #kT$} ³ –#«$kT " Õ#LkTL $

Substitusikan persamaan (2.18) ke dalam persamaan (2.17), sehingga

dipero-leh

–#« " kT$ - –#«$ " k³–#«$ T

X –#«$ " k³–#«$ T "k_{2 T} ³ –#«$T " Õ#LkTL $ - –#«$ " k³–#«$ T

X1_{2 k T} ³ –#«$T " Õ#LkTL $ - 0

Bagi dengan k dan misalkan k ™ 0, sehingga diperoleh T ³ –#«$T - 0.

▄

Teorema 2.3.3

Misalkan –, — adalah fungsi konveks pada himpunan { v , maka – " —

juga adalah fungsi konveks pada S.

Bukti:

Misalkan , { dan 0 o ¿ o 1, maka

–#¿ " #1 ¿$ $ " —#¿ " #1 ¿$ $ S ¿–# $ " #1 ¿$– " ¿—# $ " #1 ¿$—

S ¿ –# $ " —# $ " #1 ¿$ –# $ " —# $

Teorema 2.3.4 (Teorema Proyeksi)

Misalkan { v adalah himpunan konveks tertutup tidak kosong dan B Ö {,

maka ada titik tunggal « { dengan jarak minimum dari y, yakni

LB «L inf_×LB L #2.19$

Selanjutnya, « adalah titik minimum dari persamaan (2.19) jika dan hanya jika

AB «, «C S 0, { (2.20)

atau dapat dikatakan bahwa « adalah proyeksi Ù_×#B$ dari y di S jika dan hanya jika persamaan (2.20) dipenuhi.

Bukti:

Pembuktian Teorema 2.3.4 di atas dapat dibagi menjadi tiga bagian, yakni:

(i) Akan dibuktikan bahwa jika { v adalah himpunan konveks

tertu-tup tidak kosong dan B Ö {, maka ada titik tunggal « { dengan jarak

minimum dari y, yakni LB «L inf _×LB L. Misalkan

inf8LB L| {< Ú ' 0 (2.21)

Karena Ú adalah batas bawah terbesar maka Ú S LB L, {.

ti-tik y, diperoleh titik ₂. Kemudian, dari titik ₂ dibuat kitar dengan

ra-dius 1

2. Dari titik limit yang diperoleh dari kitar 2 dan berada pada ga-ris yang menghubungkan titik ₂ dan titik y, diperoleh titik ₃. Demi-kian seterusnya, hingga diperoleh titik _{Û 1}. Kemudian dari titik _{Û 1}

dibuat kitar dengan radius 1_Û. Dari titik limit yang diperoleh dari kitar

Û 1 tersebut dan terletak pada ruas garis yang menghubungkan titik Û 1 dan titik y diperoleh titik _Û. Dengan demikian akan ada barisan 8 _Û<v {.

Akan ditunjukkan bahwa LB _ÛL™ Ú.

Karena Ú inf8LB L| {< maka berdasarkan Lemma 2.1.1,

un-tuk setiap Š

˜ ' 0 terdapat LB ÛL dengan Û { sedemikian

se-hingga Ú "

˜' LB ˜L.

Dengan demikian, terbentuk barisan 8LB _ÛL< yang terbatas dan tu-run.

Berdasarkan Teorema 2.1.7, maka 8LB _ÛL< akan konvergen dan lim

Û™∞LB ÛL Ú inf8LB ÛL<.

Melalui Teorema Paralelogram diketahui bahwa L " BL "

L BL 2#L L " LBL $. Misalkan ambil _˜, {, di mana x

diganti dengan _˜ B dan B diganti dengan B. Dengan men-substitusikan x dan y ke dalam Teorema Paralelogram, diperoleh

L# ˜ B$ " # B$L " L# ˜ B$ # B$L 2L ˜ BL "2L BL

L _˜" 2BL " L ˜ L 2L ˜ BL " 2L BL L _˜ L 2L ˜ BL " 2L BL L ˜" 2BL

2L ˜ BL " 2L BL Ü´ ˜"₂ Bµ 2Ü

2L ˜ BL " 2L BL 4 Ü ˜"₂ BÜ #2.22$

Karena 8 _˜<⊂{ , maka # _˜" $/2 {. Dari definisi Ú dikatakan

bahwa inf LB L Ú, sehingga LB L L BL - Ú, {.

Dengan mengganti # _˜" $/2 diperoleh

Ü ˜"₂ BÜ - Ú

X Ü ˜"₂ BÜ - Ú #2.23$

Dengan menggunakan persamaan (2.22) dan (2.23) diperoleh

L _˜ L S 2L ˜ BL " 2L BL 4Ú .

2Ú " 2Ú 4Ú 0 atau L _˜ L ™ 0, yang mana menunjukkan

bahwa 8 _˜< adalah barisan Cauchy dengan limit «. Karena S tertutup, maka « {. Hal ini menunjukkan bahwa ada « sedemikian sehingga

LB «L Ú.

Selanjutnya, akan dibuktikan ketunggalan.

Andaikan Ý tidak tunggal, artinya ada Ý′ { dan Ý′ Ýdengan

LÝ′ BL Ú.

Melalui Hukum Parallelogram, misalkan diganti dengan Ý′ Bdan

Bdiganti dengan Ý B, maka diperoleh

LÝ′"Ý 2BL2"LÝ′ ÝL2 2LÝ′ BL2" 2LÝ BL2 LÝ′ ÝL2 2LÝ′ BL2" 2LÝ BL2 LÝ′"Ý 2BL2

2L«′ BL " 2L« BL Ü2 ´«′" «

2 BµÜ

2L«′ BL " 2L« BL 4 Ü«′" «

2 BÜ

2Ú " 2Ú 4 Ü«′" «₂ BÜ

Karena «"«₂ ′ {, maka menurut (2.23), Ú2SÞ«′"«₂ BÞ2.

Akibatnya,

Jadi, LÝ′ ÝLS 0, padahal LÝ′ ÝL' 0. Jadi, ada kontradiksi.

Ter-bukti Ý′ Ý.

(ii) Akan dibuktikan bahwa jika AB «, «C S 0, {, maka «

ada-lah titik minimum dari LB «L inf ×LB L.

Ambil x sebarang di S dan misalkan AB «, «C S 0, {

dipe-nuhi, sehingga LB L LB « " « L

LB «L " L« L " 2AB «, « C LB «L " L« L " 2#« $ #B «$

Karena L« L - 0 dan #« $ #B «$ - 0, maka

LB L - LB «L dan « adalah titik minimum dari LB «L inf ×LB L.

(iii) Akan dibuktikan bahwa jika « adalah titik minimum dari

LB «L inf ×LB L, maka AB «, «C S 0, {.

Misalkan LB L - LB «L , {.

Karena « " k# «$ { dengan k #0,1$, maka diperoleh

LB #« " k# «$$L - LB «L X LB « k# «$L - LB «L

X LB «L " k L« L " 2k#« $ #B «$ - LB «L

X LB «L " k L «L " 2k# «$ #« B$ - LB «L X k L «L " 2k# «$ #« B$ - 0

Bagi dengan k dan misalkan k ™ 0, maka diperoleh

AB «, «C S 0, {.

▄

D. Teori Optimisasi

Secara umum, bentuk baku untuk permasalahan optimisasi berkendala

adalah sebagai berikut:

minimumkan_ß –# $ (2.24)

dengan kendala ci(x) = 0, i à (2.25)

ci(x) ≥ 0, i á (2.26) dimana:

f adalah fungsi obyektif

à = {1, … , me} adalah himpunan indeks dari kendala persamaan

á = {me + 1, … , m} adalah himpunan indeks dari kendala

pertidak-samaan

Apabila fungsi obyektif dan kendala dari permasalahan (2.24)-(2.26)

merupa-kan fungsi konveks, maka permasalahan tersebut merupamerupa-kan permasalahan

pemrograman konveks.

Definisi 2.4.1 (Titik Layak atau Penyelesaian Layak)

Titik dikatakan titik layak atau penyelesaian layak dari masalah

op-timisasi jika dan hanya jika memenuhi persamaan (2.25) dan (2.26).

Definisi 2.4.2 (Titik Optimum atau Penyelesaian Optimum)

Titik â dikatakan titik optimum atau penyelesaian optimum dari

masalah optimisasi jika dan hanya jika merupakan penyelesaian layak yang

mengoptimumkan fungsi obyektif.

Definisi 2.4.3 (Titik Stasioner atau Titik Kritis)

Titik â dikatakan titik stasioner atau titik kritis untuk f yang terdife-rensial jika ³–# â$ 0.

Definisi 2.4.4 (Himpunan Layak atau Daerah Layak)

Himpunan semua titik layak dikatakan himpunan layak atau daerah layak

yang dinotasikan dengan X, dimana X didefinisikan sebagai

atau

‘ 8 |l# $ 0, ] à;l# $ - 0, ] á<

Definisi 2.4.5 (Peminimum Global dan Peminimum Global Tegas)

Jika â ‘ dan jika –# $ - –# â$, ‘, maka â dikatakan peminimum global dari permasalahan (2.24) – (2.26). Jika â ‘dan jika

–# $ ' –# â_{$, ‘, maka} â _{dikatakan peminimum global tegas.}

Definisi 2.4.6 (Peminimum Lokal dan Peminimum Lokal Tegas)

Jika â ‘ dan jika ada suatu kitar B( â, ¡$ dari â sedemikian sehingga –# $ - –# â_{$, ‘ è x#} â_{, ¡$, maka} â _{dikatakan peminimum lokal dari}

permasalahan (2.24) – (2.26), dimana x# â, ¡$ 8 |L âL S ¡< dan ¡ ' 0. Jika â ‘ dan jika ada suatu kitar B( â, ¡$ dari â sedemikian

se-hingga –# $ ' –# â$, ‘ è x# â, ¡$, â, maka â dikatakan pemi-nimum lokal tegas.

Definisi 2.4.7 (Himpunan Indeks)

Misalkan á# $ 8]|l# $ 0, ] á<. Untuk sebarang , himpunan é# $ à ê á# $ adalah himpunan indeks dari kendala-kendala aktif di x,