BAB I PENGERTIAN DAN KEGUNAAN LOGIKA

_______________________________________________

BAB I

PENGERTIAN DAN KEGUNAAN LOGIKA

1.1 Kompetensi

Mahasiswa diharapkan mampu menguasai dan mengembangkan ilmu pengetahuan dasar, dengan logika yang dimiliki akan mampu memikirken sesuatu dengan menalar.

Dalam penalaran, manusia menggunakan logika untuk mengatur alur pemikiran serta memisahkan hal yang benar dan yang salah. Dalam Bab ini akan dipelajari beberapa pengetahuan dasar dari logika matematika sehingga mahasiswa mampu menjelaskan pengertian dan pentingnya belajar logika, dasar-dasar logika, sejarah dan perkembangan logika, jenis dan kegunaan logika, aliran-aliran dalam logika, fungsi dan kegunaan bahasa, serta beberapa perbedaan antara bahasa umum dengan bahasa matematika.

1.2 Pengertian logika Matematika

Setiap orang pasti bertanya, apa itu logika? Logika berasal dari kata yunani kuno λόγος (logos) yang berarti hasil pertimbangan dari akal fikiran yang diutarakan lewat kata- kata dan dinyatakan dalam bahasa. Logika sering dikatakan sebagai salah satu cabang dari filsafat. Sebagai ilmu, logika disebut dengan logica scientia atau ilmu logika (ilmu pengetahuan) yang mempelajari kecakapan untuk berfikir secara lurus, teratur dan tepat. [Hendrik JR, 1996]. Ilmu disini mengacu pada kemampuan rasional mengetahui dan kecakapan mengacu pada kesanggupan akal budi untuk mewujudkan pengetahuan ke dalam tindakan. Kata logis yang dipergunakan tersebut bisa diartikan dengan masuk akal.

Logika, lahir bersamaan dengan filsafat di Yunani. Dalam usaha untuk menaruh pikiran-pikirannya, pendapat-pendapatnya, filosuf-filosuf Yunani kuno tidak jarang mencoba membantah pikiran lain dengan menunjukkan kesesatan penalarannya. Seringkali logika diartikan sebagai ilmu untuk berfikir dan menalar dengan benar sehingga didapatkan kesimpulan yang absah. Manusia mampu mengembangkan pengetahuan karena mempunyai bahasa dan kemampuan menalar. Untuk dapat menarik konklusi/kesimpulan yang tepat, diperlukan kemampuan menalar. Kemampuan menalar adalah kemampuan untuk menarik konklusi yang tepat dari bukti-bukti yang ada, dan menurut aturan-aturan tertentu.

Logika membantu untuk mengatur pemikiran kita dalam memisahkan hal yang benar dari yang salah. Sering kali kita membuat asumsi/anggapan yang salah terhadap sesuatu hal, hanya karena salah menginterprestasikan/menafsirkan. Disini logika/logika simbolik, dapat membantu kita menghindari salah penafsiran, dan meningkatkan daya berfikir secara analitis. Simbol-simbol atau notasi dalam logika merupakan sarana yang sangat penting dalam melakukan penalaran.

Notasi dalam logika adalah suatu alat atau perangkat untuk mengekpresikan suatu obyek (dapat berupa benda, kalimat, bilangan-bilangan, dan sebagainya), karena dengan adanya notasi (simbol) dapat menyatakan secara singkat kalimat verbal yang panjang menjadi kalimat yang singkat (pendek) dan penuh arti. Kalimat verbal yang berlebihan cenderung tidak jelas, dan sebaliknya penggunaan notasi yang berlebihan juga cenderung

membuat materi itu menjadi sulit untuk dipelajari. Oleh karena itu penggunaan notasi harus dijaga agar tidak menghilangkan kelengkapan makna kalimat yang diwakili.

Contoh (1.1):

Ada sebuah bilangan yang jika ditambah dengan 2 menghasilkan 5. Cari bilangan itu!

Masalah di atas dapat ditulis dengan kalimat yang lebih singkat (pendek):

“Selesaikan persamaan x 2 5”.

Ada beberapa catatan dalam penggunaan notasi diantaranya adalah: untuk menunjuk obyek yang spesifik gunakan huruf / simbol tertentu, setiap huruf / simbol dapat digunakan untuk mewakili suatu obyek, ada simbol-simbol tertentu yang mewakili obyek-obyek tertentu.

Penggunaan simbul harus konsisten, sekali sebuah simbol sudah dipakai untuk mewakili suatu obyek, harus digunakan secara konsisten untuk mewakili hanya obyek itu saja. Logika simbolis merupakan logika formal yang cenderung bersifat teknis dan ilmiah.

Logika simbolis merupakan ilmu tentang bagaimana menyimpulkan yang sah (absah), khususnya yang dikembangkan dengan penggunaan metode-metode matematika dan dengan bantuan simbol-simbol khusus sehingga dapat terhindar dari makna arti ganda dari bahasa sehari-hari.

Pemakaian simbol-simbol matematika itu untuk mewakili bahasa. Simbol-simbol itu diolah sesuai dengan aturan-aturan yang diberlakukan di bidang matematika untuk menetapkan apakah pernyataan bernilai benar atau salah. Demikian juga ketidakjelasan berbahasa dapat dihindari dengan menggunakan simbol-simbol ini, karena setelah problem diterjemahkan ke dalam notasi simbolik, penyelesaiannya menjadi bersifat sederhana 1.3 Dasar-dasar Logika Matematika

Konsep bentuk logis adalah inti dari logika. Konsep itu menyatakan bahwa kesahihan (validitas) dari sebuah argumen ditentukan oleh bentuk logisnya, bukan oleh isinya. Dalam hal ini logika menjadi alat untuk menganalisis argumen, yakni hubungan antara kesimpulan dan bukti atau bukti-bukti yang diberikan (premis). Logika silogistik tradisional Aristoteles dan logika simbolik modern adalah contoh-contoh dari logika formal. Dasar penalaran dalam logika ada dua, yakni deduktif dan induktif.

1.3.1 Penalaran Deduktif.

Penalaran deduktif, kadang disebut logika deduktif, adalah penalaran yang membangun atau mengevaluasi argumen deduktif. Argumen dinyatakan deduktif jika kebenaran dari kesimpulan ditarik atau merupakan konsekuensi logis dari premis- premisnya. Argumen deduktif dinyatakan valid atau tidak valid, bukan benar atau salah.

Sebuah argumen deduktif dinyatakan valid jika dan hanya jika kesimpulannya merupakan konsekuensi logis dari premis-premisnya.

Contoh (1.2) argumen deduktif:

Premis 1: Setiap mamalia punya sebuah jantung Premis 2: Semua kuda adalah mamalia

--- Kesimpulan: Setiap kuda punya sebuah jantung

______________________________________________

Pembuktian melalui deduksi adalah sebuah jalan pemikiran yang mengguna kan argumen-argumen deduktif untuk beralih dari premis-premis yang ada, yang dianggap benar, kepada kesimpulan-kesimpulan, yang mestinya benar apabila premis-premisnya benar. Penalaran deduktif didukung oleh logika deduktif. Metode deduksi sifatnya pasti.

Berikut ini adalah contoh logika deduksi:

Contoh (1.3) argumen deduktif:

Premis 1 : Semua manusia fana (pasti akan mati). (premis mayor) Premis 2 : Socrates adalah manusia (premis minor)

--- Kesimpulan : Sokrates pasti (akan) mati.

"Socrates pasti mati" adalah kesimpulan atau konsekuensi dari dua premis sebelumnya.

Jika premis 1 dan premis 2 benar, maka kesimpulannya juga benar.

1.3.2 Penalaran Induktif

Sebagai alternatif dari penalaran deduktif adalah penalaran induktif. Perbedaan dasar di antara keduanya dapat disimpulkan dari dinamika deduktif dengan progresi secara logis dari bukti-bukti umum kepada kebenaran atau kesimpulan yang khusus; sementara dengan induksi, dinamika logisnya justru sebaliknya. Penalaran induktif dimulai dengan pengamatan khusus yang diyakini sebagai model yang menunjukkan suatu kebenaran atau prinsip yang dianggap dapat berlaku secara umum.

Penalaran induktif adalah proses berpikir untuk menarik kesimpulan berupa prinsip atau sikap yang berlaku umum berdasarkan atas fakta-fakta yang bersifat khusus.

Prosesnya disebut induksi. Penalaran induktif dapat berbentuk generalisasi, analogi, atau hubungan sebab akibat. Penalaran induktif, kadang disebut logika induktif, yaitu penalaran yang berangkat dari serangkaian fakta-fakta khusus untuk mencapai kesimpulan umum.

Contoh (1.4) argumen induktif:

Premis 1 : Kuda Sumba punya sebuah jantung Premis 2: Kuda Australia punya sebuah jantung Premis 3: Kuda Amerika punya sebuah jantung Premis 4: Kuda Inggris punya sebuah jantung --- Kesimpulan: Setiap kuda punya sebuah jantung

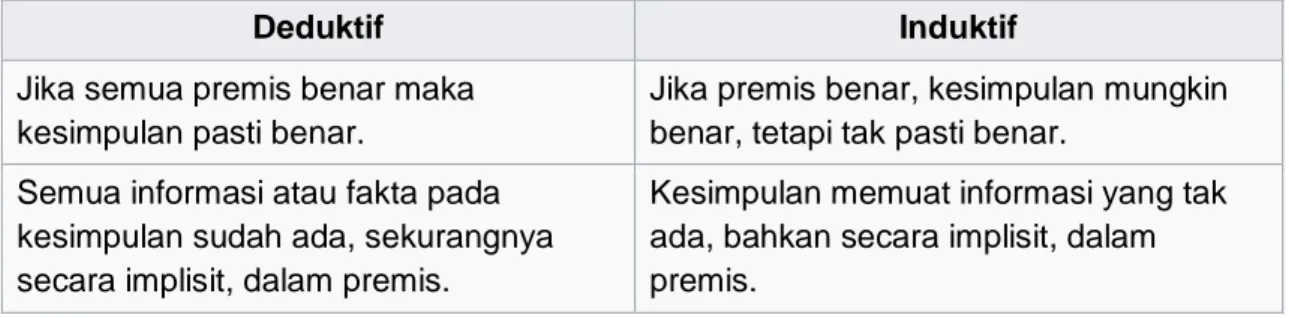
Tabel di bawah ini menunjukkan beberapa ciri utama yang membedakan penalaran induktif dan deduktif.

Deduktif Induktif

Jika semua premis benar maka kesimpulan pasti benar.

Jika premis benar, kesimpulan mungkin benar, tetapi tak pasti benar.

Semua informasi atau fakta pada kesimpulan sudah ada, sekurangnya secara implisit, dalam premis.

Kesimpulan memuat informasi yang tak ada, bahkan secara implisit, dalam premis.

1.4 Sejarah Logika dan Perkembangannya 1.4.1 Masa Yunani Kuno

Manusia belajar logika sejak Jaman Yunani Kuno. Aristoteles (384 - 322 SM) adalah seorang filsuf yang mengembangkan logika pada jaman itu, yang pada waktu itu dikenal dengan sebutan logika tradisional.

Mulai sejak Thales (624 SM - 548 SM), filsuf Yunani pertama yang memperkenalkan logika dan meninggalkan segala dongeng, takhayul, dan cerita-cerita isapan jempol dan berpaling kepada akal budi untuk memecahkan rahasia alam semesta. Thales mengatakan bahwa air adalah arkhe (Yunani) yang berarti prinsip atau asas utama alam semesta. Saat itu Thales telah mengenalkan logika induktif.

Dalam logika Thales, air adalah arkhe alam semesta, yang menurut Aristoteles disimpulkan dari: Air adalah jiwa tumbuh-tumbuhan (karena tanpa air tumbuhan mati), Air adalah jiwa hewan dan jiwa manusia, Air jugalah uap, dan Air jugalah es. Jadi, air adalah jiwa dari segala sesuatu, yang berarti air adalah arkhe alam semesta. Sejak saat Thales sang filsuf mengenalkan pernyataannya, logika telah mulai dikembangkan. Kaum Sofis beserta Plato (427 SM – 347 SM) juga telah merintis dan memberikan saran-saran dalam bidang ini.

Aristoteles kemudian mengenalkan logika sebagai ilmu, yang kemudian disebut logica scientica. Aristoteles mengatakan bahwa Thales menarik kesimpulan bahwa air adalah arkhe alam semesta dengan alasan bahwa air adalah jiwa segala sesuatu.

Pada masa Aristoteles logika masih disebut dengan analitica, yang secara khusus meneliti berbagai argumentasi yang berangkat dari proposisi yang benar, dan dialektika yang secara khusus meneliti argumentasi yang berangkat dari proposisi yang masih diragukan kebenarannya. Inti dari logika Aristoteles adalah silogisme.

Buku Aristoteles to Oraganon (alat) berjumlah enam, yaitu:

1) Categoriae menguraikan pengertian-pengertian 2) De interpretatione tentang keputusan-keputusan 3) Analytica Posteriora tentang pembuktian.

4) Analytica Priora tentang silogisme.

5) Topica tentang argumentasi dan metode berdebat.

6) De sohisticis elenchis tentang kesesatan dan kekeliruan berpikir.

Pada 370 SM – 288 SM Theophrastus, murid Aristoteles yang menjadi pemimpin Lyceum, melanjutkan pengembangan logika. Istilah logika untuk pertama kalinya dikenalkan oleh Zeno dari Citium (334 SM – 226 SM) pelopor Kaum Stoa. Sistematisasi logika terjadi pada masa Galenus (130 M – 201 M) dan Sextus Empiricus 200 M, dua orang dokter medis yang mengembangkan logika dengan menerapkan metode geometri.

Porohyus (232 – 305) membuat suatu pengantar (eisagoge) pada Categoriae, salah satu buku Aristoteles. Boethius (480-524) menerjemahkan Eisagoge Porphyrius ke dalam bahasa Latin dan menambahkan komentar- komentarnya. Johanes Damascenus (674- 749)) menerbitkan Fons Scienteae.

1.4.2 Abad pertengahan dan logika modern

Pada abad ke 9-15, buku-buku Aristoteles seperti De Interpretatione, Eisagoge oleh Porphyus dan karya Boethius masih digunakan Thomas Aquinas (1224-1274) dan kawan-

______________________________________________

kawannya berusaha mengadakan sistematisasi logika. Kemudian Lahirlah logika modern dengan tokoh-tokoh seperti: Petrus Hispanus (1210 - 1278), Roger Bacon (1214 - 1292), Raymundus Lullus (1232-1315) yang menemukan metode logika baru yang dinamakan Ars Magna, yang merupakan semacam aljabar pengertian, William Ocham (1295-1349)

Pengembangan dan penggunaan logika Aristoteles secara murni diteruskan oleh Thomas Hobbes (1588-1679) dengan karyanya Leviatan dan John Locke (1632-17040) dalam An Essay Concerning Human Understanding. Francis Bacon (1561-1626) mengembangkan logika induktif yang diperkenalkan dalam bukunya Novum Organum Scientiarum. J.S. Mills (1806-1873) melanjutkan logika yang menekankan pada pemikiran induksi dalam bukunya System of Logic.

Kemudian logika diperkaya dengan hadirnya pelopor-pelopor logika simbolik seperti:

Gottfried Wilhelm Leibniz (1646-1716) menyusun logika aljabar berdasarkan Ars Magna dari Raymundus Lullus. Logika ini bertujuan menyederhanakan pekerjaan akal budi dan lebih mempertajam kepastian.

George Boole (1815-1864), seorang matematikawan Inggris, merupakan peletak dasar bagi sistem logika yang sekarang dikenal sebagai logika Boole dan merupakan fondasi dari komputer modern.

John Venn (1834-1923) telah menulis tiga buku logika: The Logic of Chance, yang memperkenalkan interpretasi frekuensi atau frekuensi teori probabilitas pada 1866, Symbolic Logic yang memperkenalkan diagram Venn pada 1881, dan The Principles of Empirical Logic pada tahun 1889.

Gottlob Frege (1848-1925) adalah seorang matematikawan ahli logika, dan filsuf Jerman. Dia dianggap sebagai salah satu pendiri logika modern dan berkontribusi besar dalam pengembangan matematika. Dia umumnya dianggap sebagai bapak filsafat analitik, karena tulisan-tulisannya tentang filsafat bahasa dan matematika. Dalam bukunya yang berjudul Begriffsschrif , eine der arithmetischen nachgebildete Formelsprache des reinen Denkens , ia membuat terobosan baru dengan membuat perlakuan yang ketat dari konsep- konsep fungsi dan variabel. Frege ingin menunjukkan bahwa matematika tumbuh dari logika, tetapi dengan demikian, ia menciptakan teknik yang membawanya jauh melampaui logika silogisme Aristotelian dan logika proposisional Stoic yang telah ia pelajari sebagai logika tradisional.

Akibatnya, Frege menemukan logika predikat aksiomatik seperti variabel kuantifikasi yang pada akhirnya dipakai dimana-mana dalam matematika dan logika, serta memecahkan masalah perumuman ganda (multiple generality). Pada awalnya, logika hanya menangani konstanta-konstanta logika dan konektor dan, atau, jika...maka..., beberapa, dan semua. Namun iterasi dari operasi-operasinya, khususnya untuk kuantor beberapa dan semua masih kurang dipahami. Bahkan perbedaan antara sepasang kalimat seperti "setiap anak lelaki mencintai beberapa gadis" dan "beberapa gadis dicintai oleh setiap anak laki-laki " masih sulit untuk dipahami. Dengan formalisme dari Frege, kita tidak mengalami kesulitan untuk memahami pernyataan " setiap anak laki-laki mencintai beberapa gadis yang mencintai beberapa anak laki-laki yang mencintai beberapa gadis ".

Lalu Chares Sanders (1839-1914), seorang filsuf Amerika Serikat yang pernah mengajar di John Hopkins University, melengkapi logika simbolik dengan karya-karya tulisnya. Ia memperkenalkan dalil Peirce (Peirce's Law) yang menafsirkan logika selaku teori umum mengenai tanda (general theory of signs)

Puncak kejayaan logika simbolik terjadi pada tahun (1910 - 1913) dengan terbitnya Principia Mathematica tiga jilid yang merupakan karya bersama Alfred North Whitehead (1861-1914) dan Bertrand Arthur William Russel (1872-1970). Logika simbolik lalu diteruskan oleh Ludwig Wittgenstein (1889-1951), Rudolf Carnap (1891-1970), Kurt Godel (1906-1978), dan lain-lain.

1.4.3 Logika Sebagai Matematika Murni

Logika masuk ke dalam kategori matematika murni karena matematika adalah logika yang tersistematisasi. Matematika adalah pendekatan logika kepada metode ilmu ukur yang menggunakan tanda-tanda (simbol-simbol) matematik (logika simbolik). Logika tersistemati-sasi dikenalkan oleh dua orang dokter medis, Galenus (130-201 M) dan Sextus Empiricus (sekitar 200 M) yang mengembangkan logika dengan menerapkan metode geometri.

Puncak logika simbolik terjadi pada tahun 1910-1913 dengan terbitnya Principia Mathematica tiga jilid yang merupakan karya bersama Alfred North Whitehead (1861-1914) dan Bertrand Arthur William Russel (1872-1970).

1.5 Jenis Dan Kegunaan Logika 1.5.1 Jenis-jenis Logika

Secara garis besar, logika dapat digolongkan ke dalam dua jenis yakni logika alamiah dan logika ilmiah

(a). Logika alamiah

Logika alamiah adalah kinerja akal budi manusia yang berpikir secara tepat dan lurus sebelum dipengaruhi oleh keinginan-keinginan dan kecenderungan-kecenderungan yang subyektif. Kemampuan logika alamiah manusia ada sejak lahir. Logika ini bisa dipelajari dengan memberi contoh penerapan dalam kehidupan nyata.

(b). Logika ilmiah

Logika ilmiah memperhalus, mempertajam pikiran, serta akal budi. Logika ilmiah menjadi ilmu khusus yang merumuskan azas-azas yang harus ditepati dalam setiap pemikiran. Berkat pertolongan logika ilmiah inilah akal budi dapat bekerja dengan lebih tepat, lebih teliti, lebih mudah, dan lebih aman. Logika ilmiah dimaksudkan untuk menghindarkan kesesatan atau, paling tidak, dikurangi.

1.5.2 Kegunaan Logika

Kegunaan logika matematika yang dikutip dari sumber Wikipedia adalah

 Membantu setiap orang yang mempelajari logic a untuk berpikir secara rasional, kritis, lurus, tetap, tertib, metodis dan masuk akal dalam memecahkan suatu masalah

 Meningkatkan kemampuan berpikir secara abstrak, cermat, dan objektif.

 Menambah kecerdasan dan meningkatkan kemampuan berpikir secara tajam dan mandiri.

 Memaksa dan mendorong orang untuk berpikir sendiri dengan menggunakan asas- asas sistematis

______________________________________________

 Meningkatkan cinta akan kebenaran dan menghindari kesalahan-kesalahan berpkir, kekeliruan, serta kesesatan.

 Mampu melakukan analisis terhadap suatu kejadian.

 Terhindar dari klenik, gugon-tuhon (bahasa Jawa)

 Meningkatkan citra diri seseorang.

1.6 Aliran dalam logika

Aliran dalam logika matematika terdiri atas 5 aliran besar, yaitu : (a) Aliran Logika Tradisional:

Logika ditafsirkan sebagai suatu kumpulan aturan praktis yang menjadi petunjuk pemikiran.

(b) Aliran Logika Metafisis:

Susunan pikiran itu dianggap kenyataan, sehingga logika dianggap seperti metafisika.

Tugas pokok logika adalah menafsirkan pikiran sebagai suatu tahap dari struktur kenyataan. Sebab itu untuk mengetahui kenyataan, orang harus belajar logika lebih dahulu.

(c) Aliran Logika Epistemologis:

Dipelopori oleh Francis Herbert Bradley (1846 - 1924) dan Bernard Bosanquet (1848 - 1923). Untuk dapat mencapai pengetahuan yang memadai, pikiran logis dan perasaan harus digabung. Demikian juga untuk mencapai kebenaran, logika harus dihubungkan dengan seluruh pengetahuan lainnya.

(d) Aliran Logika Instrumentalis (Aliran Logika Pragmatis):

Dipelopori oleh John Dewey (1859 - 1952). Logika dianggap sebagai alat (instrumen) untuk memecahkan masalah.

(e) Aliran Logika Simbolis:

Dipelopori oleh Leibniz, Boole dan De Morgan. Aliran ini sangat menekankan penggunaan bahasa simbol untuk mempelajari secara terinci, bagaimana akal harus bekerja. Metode-metode dalam mengembangkan matematika banyak digunakan oleh aliran ini, sehingga aliran ini berkembang sangat teknis dan ilmiah serta bercorak matematika, yang kemudian disebut Logika Matematika (Mathematical Logic). G.W.

Leibniz (1646 - 1716) dianggap sebagai matematikawan pertama yang mempelajari Logika Simbolik.

Pada abad kesembilan belas, George Boole (1815 - 1864) berhasil mengembangkan Logika Simbolik. Bukunya yang berjudul Low of Though mengembangkan logika sebagai sistem matematika yang abstrak. Logika Simbolik ini merupakan logika formal yang semata- mata menelaah bentuk dan bukan isi dari apa yang dibicarakan.

1.7 Fungsi dan Kegunaan Bahasa

Secara umum, bahasa dalam kehidupan sehari-hari digunakan antara lain untuk menyampaikan informasi, memberikan informasi dan pendapat kepada orang lain, mengungkapkan isi hati dan perasaan (Bahasa para penyair), melarang melakukan sesuatu atau mengharuskan melakukan sesuatu (Bahasa para Pemuka Agama), dan lain-lainnya.

Jadi bahasa adalah alat komunikasi. Bahasa di bidang matematika berfungsi untuk menyatakan fakta-fakta secara eksak.

Yang dimaksud bahasa sebagai alat komunikasi yang diciptakan dan digunakan untuk mencapai tujuan. Dan diketahui bahwa tidak ada alat yang sempurna yang dapat mencapai segala tujuan. Contohnya: gunting cukur hanya cocok untuk mencukur rambut, tetapi tidak mampu untuk menggergaji pohon. Sebaliknya, gergaji sangat efisien untuk memotong pohon, tetapi tidak akan digunakan untuk memotong rambut.

Bahasa umum dengan segala keunggulannya sebagai bahasa “pergaulan” tidak cocok untuk menyajikan uraian-uraian matematika. Hal ini disebabkan karena bahasa umum dipandang dari sudut ke-tepat-an mempunyai banyak kelemahan, diantaranya:

mempunyai sifat yang multivalen (arti ganda), samar-samar, tidak jelas, dan juga kurang beraturan. Karena bahasa adalah amat penting, maka demi kelancaran perkembangan ilmu matematika, jika perlu, bahasa matematika terpaksa menyimpang dari kaidah-kaidah bahasa umum.

Contoh penyimpangan-penyimpangan bahasa matematika dengan bahasa umum antara lain:

Contoh (1.2):

Kata “terbesar” atau “terkecil” di suatu kelompok mahasiswa mempunyai arti mengungguli atau merendahi anggota-anggota lainnya. Sehingga jika dalam suatu kelas semua mahasiswa mempunyai berat badan 65 kg, maka:

Dalam Bahasa umum dikatakan bahwa diantara semua mahasiswa tidak ada yang mempunyai berat badan terbesar dan tidak ada yang terkecil. Dalam bahasa matematika dikatakan bahwa jika semua unsur sama, maka semua unsur tersebut dikatakan “terbesar”

dan sekaligus “terkecil”.

Contoh (1.3):

Kata “sekitar gedung”, maka Dalam bahasa umum dimaksud adalah tempat-tempat yang letaknya di dekat gedung tersebut. Dalam bahasa matematika adalah seluruh ruangan gedung tersebut dimana suatu titik terletak disebut sekitar (neighbourhood) dari titik itu.

Contoh (1.4):

Jika diantara 1.000 mahasiswa ISTA terdapat 999 mahasiswa diantaranya mempunyai sifat rajin, maka dalam bahasa umum dikatakan bahwa pada umumnya mahasiswa ISTA tersebut semuanya rajin-rajin. Sedangkan dalam bahasa matematika, pada umumnya mahasiswa ISTA tersebut tidak mempunyai sifat rajin.

Catatan: Jika ada (sekurang-kurangnya) satu anggota dalam suatu kelompok tidak memiliki sifat rajin, maka bahasa matematika dikatakan bahwa pada umumnya sifat rajin tidak dimiliki oleh para mahasiswa tersebut.

Contoh diatas merupakan beberapa penyimpangan-penyimpangan bahasa matematika terhadap bahasa umum. Dan perlu ditekankan bahwa “bahasa matematika”

tidak dimaksudkan untuk digunakan diluar matematika. Tetapi jika kaidah-kaidah bahasa umum tidak menghambat perkembangan ilmu matematika, bahasa umum tetap dapat digunakan dalam ilmu matematika (untuk kelancaran komunikasi ).

______________________________________________

1.8 Soal-Soal Latihan (Tugas)

1. Buatlah rangkuman sejarah perkembangan logika

2. Carilah 10 contoh penyimpangan-penyimpangan bahasa matematika dengan bahasa umum

===@@@@@===

BAB II

PROPOSISI DAN PENGGUNAANNYA

2.1. Kompetensi

Salah satu konsep dasar logika yang penting adalah logika proposisional. Setelah mempelajari bab ini diharapkan mahasiswa mampu dan terampil dalam menggunakan aljabar proposional dalam logika proposisional, menyajikan tabel nilai kebenaran suatu negasi, disjungsi, konjungsi, implikasi, k onvers, invers, kontraposisi, dan biimplikasi. Serta menguasai urut-urutan penggunaan kata hubung kalimat, menyusun ingkaran dari suatu pernyataan, menyatakan apakah dua pernyataan merupakan ekivalen logis, serta mengenali pernyataan yang berupa tautologi atau kontradiksi.

2.2. Arti Proposisi

Sebelum membahas tentang proposisi, kita mengingat terlebih dahulu apa yang dimaksud dengan kalimat disini. Kalimat adalah kumpulan kata-kata yang disusun menurut aturan tata bahasa. Kata yang dimaksudkan adalah rangkaian huruf yang mengandung arti.

Jadi kalimat adalah rangkaian kata-kata yang disusun menurut aturan tata bahasa dan mengandung arti.

Di dalam logika matematika, tidak semua kalimat berhubungan dengan logika. Hanya kalimat yang bernilai benar saja atau salah saja yang digunakan dalam logika. Kalimat tersebut dinamakan proposisi (preposition). Jadi Proposisi adalah kalimat logika yang merupakan pernyataan tentang hubungan antara dua atau lebih hal yang mempunyai nilai benar saja atau salah saja tetapi tidak ke dua-duanya. Sebab fakta-fakta yang ada dalam kehidupan sehari-hari itu hanya dapat disajikan dalam bentuk pernyataan matematis yang selalu mempunyai nilai benar saja atau salah saja. Secara umum bahwa tidak semua kalimat itu selalu mempunyai arti, misalnya:

(1). Harimau adalah bilangan bulat.

(2). Batu makan rumput, (3). 16 mencintai 3.

Pernyataan (1), (2), dan (3) tersebut secara gramatika merupakan kalimat, tetapi kalimat itu hanyalah sebuah rangkaian kata-kata yang tidak mempunyai arti (meaningless).

Setiap kalimat yang mempunyai arti dapat dikelompokkan menjadi dua kategori.

Kategori yang pertama misalnya:

(1). Jam berapa sekarang ? (2). Astaga!

(3). Tolong tutuplah pintu itu!

(4). Mudah-mudahan hari ini tidak hujan.

(5). Sejuk benar udara di sini!

Kalimat (1), (2), (3), (4) dan (5) walaupun secara gramatika mempunyai arti, tetapi tidak mempunyai nilai benar ataupun salah.

Sedangkan kategori yang kedua misalnya:

(1). 16 habis dibagi 4

______________________________________________

(2). 7 adalah bilangan genap,

(3). Penduduk Solo lebih banyak dari Jakarta, (4). Jerman berada di Indonesia.

Kalimat (1), (2), (3) dan (4) di atas jelas merupakan suatu pernyataan karena memiliki nilai benar saja atau salah saja. Pernyataan (1) bernilai benar, sedangkan pernyataan (2), (3) dan (4) bernilai salah.

Untuk mempermudah pemahaman, suatu proposisi mempunyai tiga unsur yaitu subyek, predikat dan kopula (penghubung antara subyek dan predikat). Misalnya “Semua manusia adalah hamba Allah”. Disini subyeknya “Semua manusia “, predikatnya

“hamba Allah “, dan kopula (penghubung antara subyek dan predikat) kata “adalah”.

Kalimat yang mempunyai nilai benar saja atau salah saja juga disebut kalimat deklaratif. Jadi proposisi (kalimat deklaratif) adalah suatu kalimat yang berarti yang mempunyai nilai benar saja atau salah saja. Selanjutnya, semua kalimat yang dibicarakan dalam buku ini hanya kalimat deklaratif dan sering disingkat sebagai “ kalimat” atau

“pernyataan” saja.

Notasi (lambang, symbol) yang digunakan dalam logika matematika disini adalah huruf kecil p, q, r …. digunakan untuk menyatakan kalimat, sedangkan symbol B atau angka 1 menyatakan benar, dan S atau angka 0 menyatakan salah

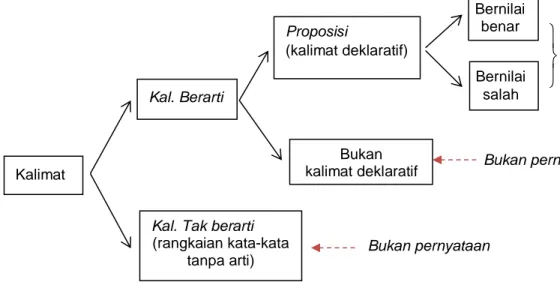
Gambar 2.1 Proposisi (kalimat deklaratif) adalah suatu pernyataan

Jadi tidak semua kalimat bisa dijadikan proposisi (kalimat deklaratif), ada yang tidak bisa dijadikan sebuah proposisi yaitu

a. Kalimat perintah b. Kalimat harapan c. Kalimat pertanyaan d. Kalimat keheranan

Beberapa contoh kalimat yang bisa dijadikan proposisi, diantaranya berupa kalimat berita, misalnya:

1. Anak-anak itu sedang bermain di tanah lapang 2. 3 + 7 < 12

3. Ada air di matahari Kalimat

Kal. Berarti

Kal. Tak berarti (rangkaian kata-kata

tanpa arti)

Proposisi

(kalimat deklaratif)

Bukan kalimat deklaratif

Bernilai benar

Bernilai salah

Bukan pernyataan

Bukan pernyataan

 



pernyataan

4. Hasan adalah guru Contoh (2.1):

(a) 31 < (13+7+9)

(b) Ini Bulan januari dan 19 < 7 (c) Jangan tidur di kelas (d) x + y > 15

(e) x < y jika dan hanya jika y > x (f) 3 + 7 = 10

(g) Kamu tinggal dimana?

(h) 4 adalah bilangan genap

Kalimat (a) dan (b) merupakan proposisi bernilai salah. Kalimat (c), (d), dan (g) bukan proposisi, sebab kalimat (c) merupakan kalimat harapan/himbauan, kalimat (d) merupakan kalimat tapi bukan proposisi, sedangkan (g) merupakan kalimat tanya. Kalimat (e), (f) dan (h) merupakan proposisi bernilai benar

2.3. Pernyataan dan Bukan Pernyataan

Ketika kita belajar tentang logika matematika, maka salah satu konsep dasar yang sangat penting untuk diingat adalah apa itu yang dimaksud pernyataan. Kita harus dapat membedakan mana kalimat yang merupakan pernyataan dan yang mana kalimat yang bukan pernyataan. Pertama-tama kita ingat bahwa semua pernyataan adalah kalimat, tetapi sebuah kalimat belum tentu merupakan pernyataan (lihat diagram gambar 2.1). Artinya tidak semua kalimat dapat digolongkan sebagai pernyataan (kalimat deklaratif) dan disebut juga proposisi. Kalimat yang tidak deklaratif tidak dapat dinyatakan sebagai pernyataan karena nilai kebenarannya sangat bergantung pada keadaan.

Jadi pernyataan adalah semua kalimat deklaratif yang bersifat pasti, bernilai benar saja atau salah saja, tidak bergantung pada keadaan. Suatu pernyataan umumnya diberi lambang huruf kecil, dan diikuti dengan tanda titik dua. Sebagai contoh pernyataan: “enam adalah bilangan genap” dapat dinyatakan sebagai p: enam adalah bilangan genap.

Salah satu cara untuk menentukan pernyataan atau bukan adalah dengan melihat atau menentukan nilai kebenaran dari pernyataan n(p). Pernyataan p yang bernilai benar ditulis n(p) = B dan bernilai salah ditulis n(p) = S.

Nilai kebenaran dari suatu pernyataan dapat ditentukan dengan dua cara yaitu a. Secara empiris: nilai kebenarannya ditentukan oleh fakta atau kebenaran umum.

b. Secara tidak empiris: nilai kebenarannya ditentukan oleh bukti atau perhitungan.

Dibawah ini diberikan contoh kalimat sebagai pernyataan dan bukan pernyataan Contoh (2.2): Beberapa contoh kalimat yang bukan pernyataan

1) Tolong tutup pintu itu (tidak deklaratif, bukan pernyataan)

2) Gedung itu sangat tinggi dan megah (nilai kebenaran tergantung fakta/keadaan, bukan pernyataan)

3) Bagaimana kabarmu sekarang? (tidak deklaratif, bukan pernyataan)

4) Enak sekali kueh buatanmu ini (nilai kebenaran tergantung fakta/keadaan, bukan pernyataan)

5) Si do’I nanti mau ke rumah (nilai kebenaran tergantung fakta/keadaan, bukan

______________________________________________

6) Tolong ambilkan sepatu itu. (Bukan kalimat deklaratif, bukan pernyataan)

7) Gedung itu sangat tinggi dan megah. (Kalimat deklaratif relatif nilainya tergantung fakta, bukan pernyataan,)

8) Bagaimana kabarmu hari ini. (Bukan deklaratif, bukan pernyataan) 9) Cabe merah yang pedas disukai anak muda. (Bukan pernyataan) 10) Semoga cepat sembuh (nilainya tergantung fakta, bukan pernyataan) Contoh (2.3): Beberapa contoh pernyataan

1) Delapan belas adalah bilangan genap (pernyataan benar) 2) Air adalah benda padat (pernyataan salah)

3) 111 habis dibagi 3 (pernyataan benar)

4) Yogyakarta adalah ibukota bali (pernyataan salah) 5) Tujuh belas ditambah 5, (pernyataan salah) 6) 3 + 9 x 5 < 50. (Pernyataan benar)

7) Batu adalah benda cair. (pernyataan salah) 8) 16 habis dibagi 4 Deklaratif, pernyataan benar

9) Tiga puluh tujuh adalah bilangan prima (deklaratif, pernyataan) 10) 34 + 3 x 2 = 109 (pernyataan bernilai salah)

Sering kali kita menjumpai pernyataan yang tidak dapat langsung ditentukan nilai kebenarannya, karena nilainya masih bergantung pada nilai variabel yang belum ada.

Karena nilai bergantung pada peubahnya, maka kalimatnya bisa saja bernilai benar atau salah. Kalimat yang seperti ini disebut kalimat terbuka (lebih rinci dibahas di bab 3). Jadi kalimat terbuka adalah kalimat yang memuat peubah, sehingga belum dapat ditentukan nilai kebenarannya.

Kalimat terbuka ini dapat diubah menjadi kalimat deklaratif (pernyataan) dengan cara memberikan nilai tertentu pada peubahnya sehingga kalimatnya bernilai benar saja atau salah saja. Berikut diberikan contoh kalimat yang belum mempunyai nilai kebenaran (bukan kalimat deklaratif)

Contoh (2.4):

a. X adalah bilangan genap b. 3x + 5 = 10

c. N adalah bilangan prima d. Y + X < 9

e. Log n = 4

Ke 5 contoh kalimat tersebut belum merupakan pernyataan, karena nilainya masih bergantung dari peubahnya. Agar kalimat tersebut mempunyai nilai, maka harus memberi kan nilai tertentu pada peubahnya sehingga menjadi kalimat deklaratif

Pembahasan:

a. Ambil x = 4, sehingga menjadi 4 adalah bilangan genap (pernyataan bernilai benar) b. Jika x =1, maka pernyatannya menjadi 3(1) + 5 = 10. (pernyataan yang bernilai salah) c. Ambil N = 13, Maka pernyataan menjadi, 13 adalah bilangan prima (Pernyataan akan

bernilai benar)

f. Ambil X = 2 dan Y = 8, sehingga kalimatnya menjadi “8 + 2 < 9” (pernyataan bernilai salah)

d. Ambil n = 100, diperoleh log 100 = 4 (ini merupakan pernyataan salah) 2.4. Pernyataan Tunggal dan Pernyataan Majemuk

Untuk memudahkan pembicaraan selanjutnya, kalimat deklaratif akan disingkat sebagai kalimat saja atau pernyataan, dan juga kadang-kadang menyebutnya dengan proposisi. Pernyataan yang biasa kita gunakan disini dapat dibedakan menjadi pernyataan tunggal dan pernyataan majemuk.

Pernyataan Tunggal adalah pernyataan yang tidak memuat pernyataan lain, yang berdiri sendiri atau tidak mempunyai kata penghubung. Sedangkan pernyataan majemuk adalah pernyataan yang menggabungkan dua atau lebih pernyataan tunggal dan memiliki kata penghubung (kopula). Berikut diberikan contoh kalimat tunggal atau pernyataan tunggal, dan contoh pernyataan majemuk.

Contoh (2.5): Pernyataan Tunggal a. Hari ini di yogyakarta hujan deras

b. Beberapa bilangan prima adalah bilangan genap c. Aliran listrik di kantor putus

Contoh (2.6): Pernyataan Majemuk

a. Pak Bambang Sucipto mengajar matematika atau bahasa Inggris

b. Jika semua warga negara membayar pajak maka pembangunan berjalan lancar c. Cuaca hari ini cerah dan si Rudi tetap bermain sepakbola

Dengan memperhatikan contoh diatas, pernyataan majemuk terdiri atas subyek predikat dan kopula (penghubung kalimat)

2.5. Kata Hubung Logika (operator logika)

Dalam bahasa Indonesia kita sering menggunakan kata-kata “tidak”, “dan”, “atau”,

“jika. . . maka. . .”, dan “jika dan hanya jika”. Marilah sekarang kita memperhatikan penggunaan kata-kata itu dengan lebih cermat dalam logika matematika dan membanding kannya dengan penggunaan dalam percakapan sehari-hari. Kita pelajari sifat-sifatnya untuk memperjelas cara berpikir kita dan terutama karena pentingnya kata-kata itu untuk melakukan pembuktian. Dalam logika matematika, khususnya logika proporsional, kata- kata itu disebut operator logika atau kata hubung kalimat.

Logika Proposisional merupakan suatu metoda penalaran dari proposisi majemuk.

Dengan kalimat yang sederhana, dalam logika proposisional kita akan belajar, bagaimana menilai kebenaran suatu proposisi majemuk. Setiap proposisi majemuk memiliki sekurang- kurangnya satu operator logika. Dalam logika proposisonal ini untuk memudahkan penalaran terhadap proposisi majemuk, digunakan Tabel nilai Kebenaran.

Terdapat lima macam operator logika yaitu negasi, konjungsi, disjungsi, kondisional, dan bikondisional yang dinyatakan dalam tabel 2.1 di bawah ini.

______________________________________________

Tabel 2.1 Lima operator logika proposisional

No Operator Logika Nama Simbol

1. Tidak/Bukan (NOT) Negasi a. ~ atau ^{“  ”}

2. Dan, (AND)

(tetapi, meskipun, juga, sedangkan, padahal) Konjungsi Λ

3. Atau (OR) Disjungsi V

4. Jika/kalau… maka…. (IF THEN) Implikasi 

Jika dan hanya jika (IF ONLY IF) Biimplikasi 

Simbol-simbol khusus tersebut diatas kita gunakan untuk mempermudah dalam memahami konsep-konsep dasar logika proporsisional, karena dalam tata bahasa matematika urutan penggunaan operator logika tersebut sangat memperhatikan ketepatan yang setinggi-tingginya, sehingga perlu adanya penertiban dalam penggunaannya.

Penertiban tersebut dituangkan dalam bentuk daftar-daftar tabel nilai kebenaran.

2.5.1. Negasi (Ingkaran)

Dalam logika matematika, arti negasi atau ingkaran adalah operasi logika terhadap suatu pernyataan, baik tunggal maupun majemuk. Negasi dari suatu pernyataan adalah pernyataan yang nilai kebenarannya berlawanan dengan pernyataan asalnya. negasi dari pernyataan p dinotasikan dengan ~p. Jika pernyataan p bernilai benar maka pernyataan ~p bernilai salah, begitu pun sebaliknya. Negasi dari suatu pernyataan berbeda-beda tergantung dari jenis pernyataannya. Negasi dari pernyataan tunggal cukup sederhana. Kita cukup membubuhkan kata "tidak" atau "bukan" untuk menyangkal atau mengingkari pernyataan asalnya.

Sedangkan untuk negasi suatu pernyataan majemuk dan negasi dari pernyataan berkuantor ada aturan tertentu untuk menentukan negasinya. Mari kita bahas satu persatu bagaimana menentukan negasi dari suatu pernyataan.

Definisi (2.1):

Ingkaran suatu pernyataan adalah suatau pernyataan yang bernilai benar, jika pernyataan semula salah, atau sebaliknya. Negasi pernyataan p ditulis ~ p atau “p” dan diucapkan “tidak p”. Dengan tabel nilai kebenarannya sebagai berikut :

Tabel 2.2. Tabel nilai kebenaran Negasi suatu pernyataan

Contoh (2.7)

1. Misal: p: Jakarta ibu kota RI (benar, atau B)

Maka ingkarannya: ~p: Tidak benar bahwa Jakarta ibu kota RI (salah atau S) atau ~p: Jakarta bukan ibu kota RI (salah atau S)

2. Misal: q: zainal memakai kacamata (benar atau B)

Maka ingkarannya: ~q: Tidak benar bahwa zainal memakai kacamata (bernilai salah atau S)

atau ~q: zainal tidak memakai kacamata (salah atau S)

p p dibaca

B S Jika p benar maka pbernilai salah S B Jika p salah maka pbernilai benar

3. Jika r: 2 + 3 < 6 (benar atau B)

maka ingkarannya: ~r: Tidak benar bahwa 2 + 3 < 6 (salah atau S) atau ~r : 2 + 3  6 (salah atau S)

Perhatikan bahwa cara membuat ingkaran di atas, jangan membuat ingkaran yang salah. Membentuk ingkaran suatu pernyataan dapat dengan menambahkan kata-kata tidak benar bahwa di depan pernyataan aslinya, atau jika mungkin dengan menambah bukan atau tidak di dalam pernyataan itu, tetapi untuk pernyataan-pernyataan tertentu tidak demikian halnya.

2.5.2. Konjungsi

Konjungsi adalah pernyataan yang dibentuk dari dua pernyataan yang dirangkai dengan operator logika “dan”, dinyatakan dengan symbol logika “∧”. Konjungsi merupakan salah satu jenis pernyataan dalam logika matematika yang sering digunakan untuk menganalisis kebenaran dalam kasus kepolisian, biasanya digunakan untuk membuktikan suatu kejadian berdasarkan pernyataan-pernyataan yang muncul.

Dua buah pernyataan p dan q yang dihubungkan dengan operator logika “dan”

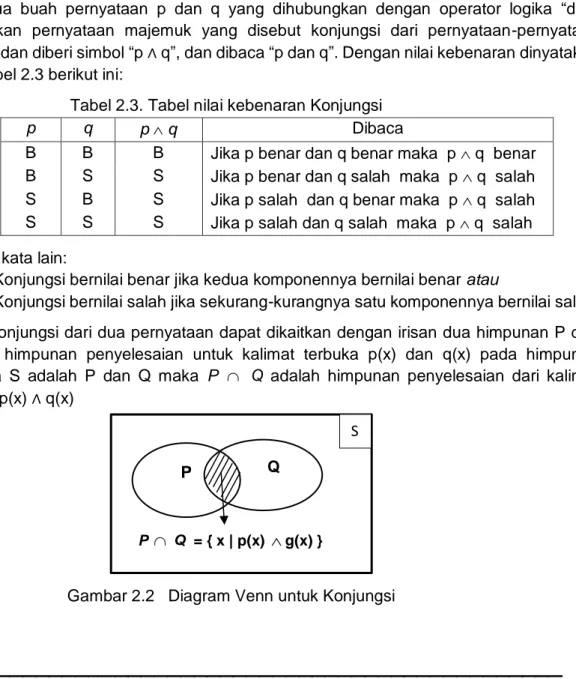
merupakan pernyataan majemuk yang disebut konjungsi dari pernyataan-pernyataan semula, dan diberi simbol “p ∧ q”, dan dibaca “p dan q”. Dengan nilai kebenaran dinyatakan pada tabel 2.3 berikut ini:

Tabel 2.3. Tabel nilai kebenaran Konjungsi

Dengan kata lain:

1. Konjungsi bernilai benar jika kedua komponennya bernilai benar atau

2. Konjungsi bernilai salah jika sekurang-kurangnya satu komponennya bernilai salah.

Konjungsi dari dua pernyataan dapat dikaitkan dengan irisan dua himpunan P dan Q. Jika himpunan penyelesaian untuk kalimat terbuka p(x) dan q(x) pada himpunan semesta S adalah P dan Q maka P  Q adalah himpunan penyelesaian dari kalimat terbuka p(x) ∧ q(x)

Gambar 2.2 Diagram Venn untuk Konjungsi

p q p  q Dibaca

B B B Jika p benar dan q benar maka p  q benar B S S Jika p benar dan q salah maka p  q salah S B S Jika p salah dan q benar maka p  q salah S S S Jika p salah dan q salah maka p  q salah

S

P  Q = { x | p(x) g(x) } P Q

______________________________________________

Contoh (2.8):

Tentukan nilai kebenaran dari konjungsi berikut ini

1. 2 + 8 =10 dan ibu kota sumatera Utara adalah Medan

2. Bali dikenal sebagai pulau dewata dan 144 adalah bilangan kuadrat 3. 3 adalah bilangan prima dan 3 adalah bilangan ganjil

4. Ima anak pandai dan cekatan 5. 2 + 3 < 6 dan 3 habisdibagi 2 Pembahasan:

(1). Misal: p: 2 + 8 =10, bernilai benar

q: ibu kota sumatera Utara adalah Medan, bernilai benar Maka p  q bernilai benar

(2). Misal: p: Bali dikenal sebagai pulau dewata, bernilai benar q :144 adalah bilangan kuadrat, bernilai benar Maka p  q bernilai benar

(3). Misal: p: 4 adalah bilangan ganjil bernilai salah q: 3 adalah bilangan prima bernilai benar Maka p  q bernilai salah

(4). Misal: p: Ima anak pandai q: cekatan

Maka p  q bernilai benar jika ima bener2 anak pandai dan bener 2 anak cekatan (5). Misal: p: 2 + 3 < 6, bernilai benar

q: 3 habis dibagi 2, bernilai salah Maka p  q bernilai salah

2.5.3. Disjungsi

Disjungsi adalah pernyataan yang dibentuk dari gabungan dua pernyataan tunggal yang dihubungkan dengan operator logika “ atau “, dan dinyatakan dengan symbol logika “

 “. Disjungsi merupakan salah satu jenis pernyataan dalam logika matematika dan konsep logika lainnya, sering digunakan untuk menganalisis kebenaran dalam kasus kepolisian, biasanya digunakan untuk membuktikan suatu kejadian berdasarkan pernyataan- pernyataan yang muncul.

Dengan melihat tabel nilai kebenaran disjungsi yang diperoleh, suatu kebenaran pernyataan akan dapat diselidiki. Terdapat dua jenis disjungsi yaitu (1). Disjungsi ekslusif dan (2). Disjungsi Inklusif. Perhatikan pernyataan berikut ini

“Tobing seorang mahasiswa yang cerdas atau seorang yang berbakat atlit”.

Dalam membaca pernyataan tersebut akan timbul dua tafsiran yaitu:

(1). Tobing seorang mahasiswa yang cemerlang saja, atau seorang yang berbakat atlit saja, tetapi tidak kedua-duanya,

(2). Tobing seorang mahasiswa yang cemerlang, atau seorang yang berbakat atlit, mungkin kedua-duanya.

Tafsiran (1) disebut disjungsi eksklusif dan diberi simbol “∨”, dan tafsiran (2) disebut disjungsi inklusif dan diberi simbol “∨"

Lebih jelasnya kita perhatikan bersama-sama definisi disjungsi inklusif dan disjungsi eksekutif di bawah ini.

Definisi(2.2): [Disjungsi inklusif]

Dua buah proposisi p dan q disebut disjungsi inklusif jika paling sedikit ada satu proposisi penyusunnya bernilai benar dan diberi notasi p  q (dibaca p atau q). Dengan tabel nilai kebenaran seperti pada tabel 2.4 dibawah ini.

Tabel 2.4. Tabel nilai kebenaran Disjungsi inklusif

Dengan kata lain bahwa:

(1). Disjungsi inklusif bernilai benar jika salah satu komponennya bernilai benar (2). Disjungsi inklusif bernilai salah jika kedua komponennya bernilai salah Berikut ini diberikan diagram Venn untuk disjungsi inklusif

Gambar 2.3. Diagram Venn untuk Disjungsi

Disjungsi dua pernyataan dapat dihubungkan dengan gabungan dua himpunan P dan Q. jika P dan Q masing-masing adalah himpunan penyelesaian dari kalimat terbuka p(x) dan q(x) pada himpunan semesta S, seperti terlihat pada gambar 2.3, maka P Q adalah himpunan penyelesaian dari kalimat terbuka p(x) q(x) pada himpunan semesta yang sama. Jika ditulis dalam bentuk notasi himpunan, maka gabungan dari dua

himpunan P dan Q dapat dituliskan: P Q = {x| p(x) q(x)}

Contoh (2.9):

(1). Dewa anak pintar atau rajin belajar

(2). Sebuah bilangan asli adalah bilangan cacah atau bulat

(3). Aku tinggal di indonesia atau aku belajar bahasa inggris sejak SMP Pembahasan:

Pada contoh (1) kata “atau” mencakup keduannya, artinya dewa merupakan anak pintar atau rajin belajar, atau bisa saja kedua-duanya yaitu dewa anak pintar sekaligus rajin.

p q p  q Dibaca

B B B Jika p benar atau q benar maka p  q benar B S B Jika p benar atau q salah maka p  q benar S B B Jika p salah atau q benar maka p  q benar S S S Jika p salah atau q salah maka p  q salah

S

P  Q = { x | p(x) g(x) } P Q

______________________________________________

Pada contoh (2) bilangan “asli” bisa saja merupakan bilangan cacah atau bilangan bulat, atau bilangan cacah sekaligus bilangan bulat

Pada contoh (3) bisa saja aku tinggal di indonesia atau aku belajar bahasa inggris sejak SMP, atau bisa aku tinggal di indonesia sekaligus belajar bahasa inggris sejak SMP Definisi (2.3): [Disjungsi eksklusif]

Dua buah proposisi p dan q disebut disjungsi eksklusif jika salah satu dari kedua proposisi penyusunnya bernilai benar. Ditulis dengan Notasi: p q (dibaca: p ataukah q).

Dengan tabel nilai kebenaran tampak pada tabel 2.7 dibawah ini Tabel 2.7. Tabel nilai kebenaran Disjungsi eksklusif

Contoh (2.10)

1. Rani naik pesawat terbang atau kapal laut

2. Akar dari bilangan rasional positif adalah rasional atau irrasional 3. Aku lahir di Surabaya atau di Bandung

Pembahasan:

Ketiga pernyataan di atas termasuk disjungsi eksklusif karena pernyataan yang dimaksudkan adalah salah satu saja dan tidak mungkin terjadi dua-duanya.

Pada contoh (1), jika Rani naik pesawat, maka dia pasti tidak naik kapal laut atau juga sebaliknya. Pada contoh ke (2), jika akar bilangan rasional positif adalah irrasional maka pasti bukan rasional atau juga sebaliknya. Dan pada contoh ke (3) jika aku benar-benar lahir di kota Surabaya pasti tidak mungkin sekaligus lahir di Bandung atau sebaliknya, (tidak mungkin terjadi pada kedua kondisi yang berbarengan).

2.5.4. Implikasi (Kondisional atau kalimat bersyarat)

Implikasi adalah pernyataan majemuk yang disusun dari dua buah pernyataan tunggal yang dirangkai menggunakan hubungan kausal (sebab akibat). Karena keduanya menunjukan hubungan sebab akibat, maka pernyataan implikasi sering juga disebut sebagai pernyataan kondisional (pernyataan bersyarat).

Implikasi diberi symbol “ “ yang dibaca jika-maka. Pernyataan pertama pada implikasi diawali dengan jika dan kalimat kedua diawali dengan maka. Bagian pertama menunjukan alasan (sebab) dan bagian kedua menunjukan kesimpulan (akibat)

Jika dua pernyataan p dan q di hubungkan dengan operator “  “ ditulis dengan symbol logika “ p  q “ dan implikasi ini dapat dibaca sebagai berikut:

1. Jika p maka q 2. p hanya jika q 3. q jika p

4. p merupakan syarat cukup bagi q

p q p  q

B B S Jika p benar atau q benar maka p  q salah B S B Jika p benar atau q salah maka p  q benar S B B Jika p salah atau q benar maka p  q benar S S S Jika p salah atau q salah maka p  q salah

5. q merupakan syarat perlu bagi p

6. p disebut anteseden (hipotesis, yang terjadi dahulu) 7. q disebut konsekuen (konklusi)

Bila kita menganggap pernyataan p dan q sebagai suatu peristiwa, maka kita melihat bahwa “Jika p maka q” dapat diartikan sebagai “Bilamana p terjadi maka q juga terjadi” atau dapat juga, diartikan sebagai “Tidak mungkin peristiwa p terjadi, tetapi peristiwa q tidak terjadi”. Agar lebih jelas pemahaman, perhatikan definisi berikut

Definisi (2.4):

Dua pernyataan p dan q di hubungkan dengan operator “  “ ditulis dengan symbol logika “ p  q “ dan disebut implikasi (pernyataan bersyarat satu arah). Implikasi p  q bernilai benar jika anteseden salah atau konsekuen benar.

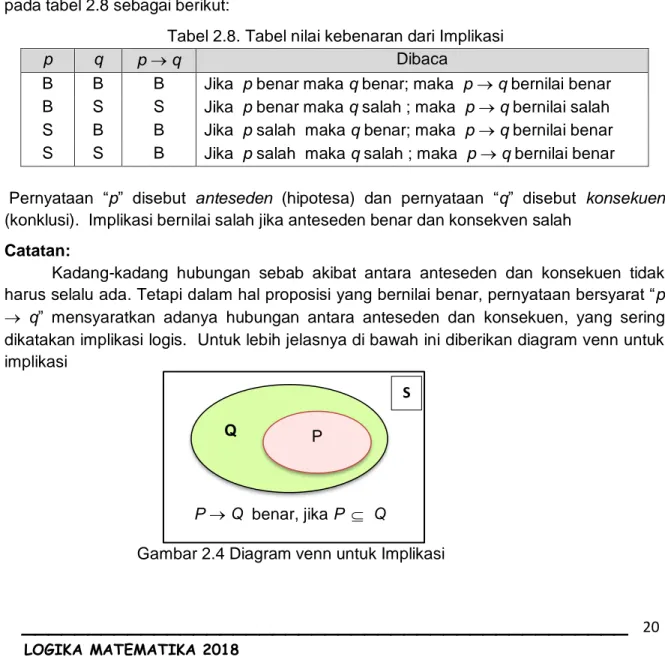
Berbeda dengan pengertian implikasi sehari-hari. Maka pengertian implikasi disini hanya ditentukan oleh nilai kebenaran dari anteseden dan konsekuennya saja, dan bukan oleh ada atau tidak adanya hubungan isi antara anteseden dan konsekuen. Implikasi ini disebut implikasi material. Sedang implikasi yang dijumpai dalam percakapan sehari-hari disebut implikasi biasa (ordinary implication). Dengan tabel nilai kebenarannya dinyatakan pada tabel 2.8 sebagai berikut:

Tabel 2.8. Tabel nilai kebenaran dari Implikasi

Pernyataan “p” disebut anteseden (hipotesa) dan pernyataan “q” disebut konsekuen (konklusi). Implikasi bernilai salah jika anteseden benar dan konsekven salah

Catatan:

Kadang-kadang hubungan sebab akibat antara anteseden dan konsekuen tidak harus selalu ada. Tetapi dalam hal proposisi yang bernilai benar, pernyataan bersyarat “p

 q” mensyaratkan adanya hubungan antara anteseden dan konsekuen, yang sering dikatakan implikasi logis. Untuk lebih jelasnya di bawah ini diberikan diagram venn untuk implikasi

Gambar 2.4 Diagram venn untuk Implikasi

p q p  q Dibaca

B B B Jika p benar maka q benar; maka p  q bernilai benar B S S Jika p benar maka q salah ; maka p  q bernilai salah S B B Jika p salah maka q benar; maka p  q bernilai benar S S B Jika p salah maka q salah ; maka p  q bernilai benar

S

P  Q benar, jika P  Q

Q P

______________________________________________

Suatu pernyataan dikatakan termasuk implikasi logis jika terdapat hubungan antara pernyataan pertama (anteseden) dan pernyataan kedua (konsekuen). Jika pada implikasi p(x)  q(x), kalimat p(x) memuat kalimat q(x) dan setiap pergantian nialai x pada p mempengaruhi kebenaran q(x), maka implikasi tersebut merupakan implikasi logis

Jika dikaitkan dengan himpunan, maka implikasi memiliki hubungan dengan himpunan bagian. Jika penyelesaian kalimat terbuka p(x) dan q(x) pada himpunan

semesta S adalah P dan Q maka implikasi P  Q benar, jika P  Q yang digambarkan pada gambar 2.4 di atas

Contoh (2.11)

Tentukan nilai kebenaran dari beberapa implikasi berikut

a. Jika 5 adalah bilangan genap, maka Medan ibukota Sumatra Utara b. Jika 6 – 1 = 5, maka 5 adalah bilangan prima

c. jika burung mempunyai sayap maka 2 + 3 = 5 d. Jika 6 + 9 = 25 maka besi adalah benda cair

e. Jika 3 hanya habis dibagi 1 dan 3, maka 3 termasuk bilangan prima Pembahasan

(a). Misal: p : 5 adalah bilangan genap (bernilai salah),

q : Medan ibukota Sumatra Utara (bernilai benar) Maka implikasi p  q bernilai benar

(b). Misal: p : 6 – 1 = 5 (bernilai benar), dan q : 5 adalah bilangan prima (bernilai benar) Maka implikasi p  q bernilai benar

(c). Misal: p : burung mempunyai sayap (bernilai benar), dan q : 2 + 3 = 7 (bernilai salah) Maka implikasi p  q bernilai salah

(d). Misal: p : 6 + 9 = 25 (bernilai salah), dan q : besi adalah benda cair (bernilai salah) Maka implikasi p  q (bernilai benar)

(e). Misal: p: 3 hanya habis dibagi 1 dan 3 (bernilai benar), dan q: 3 termasuk bilangan prima (bernilai benar). Maka implikasi p  q bernilai benar

Perhatikan contoh di atas yaitu soal nomer 5 atau e). “Jika 3 hanya habis dibagi 1 dan 3, maka 3 termasuk bilangan prima” ini merupakan implikasi logis karena pernyataan pertama (anteseden) memuat pernyataan ke dua (konsekuen), dan nilai kebenaran anteseden akan menyebabkan konsekuen bernilai benar

2.5.5. Konvers, Invers, dan Kontraposisi

Dari pernyataan yang berupa implikasi “ p  q “ dapat dibuat pernyataan implikasi baru yang berupa Konvers, Invers dan Kontraposisi. Jadi konvers, invers dan kontraposisi adalah suatu pernyataan Implikasi baru dari suatu pernyataan implikasi “ p  q “ , sehingga:

a. Konvers adalah perubahan dari implikasi ke implikasi yang lain. Pernyataan q  p disebut Konvers dari p  q.

b. Invers adalah Pembalikan suatu susunan dari suatu pernyataan yang lainnya. Jadi pernyataan ~p  ~q disebut Invers dari implikasi p  q.

c. Pernyataan ~q  ~p disebut Kontraposisi dari implikasi p  q.

Agar lebih jelas dalam menerapkannya, perlu adanya definisi yang menguatkan konsep yang berhubungan dengan konvers, invers dan kontraposisi

Definisi (2.5) :

Yang dimaksud dengan “Konvers” dari implikasi p  q adalah q  p ,

“Invers” dari implikasi p  q adalah ~ p  ~ q atau dituliskan pq, sedangkan “Kontraposisi” dari implikasi p  q adalah ~ q  ~ p atau dituliskan qp

Untuk melihat hubungan nilai kebenaran antara implikasi, konvers, invers dan kontraposisi perhatikanlah tabel nilai kebenaran, tabel 2.9 di bawah ini :

Tabel 2.9. Tabel Implikasi, invers, konvers dan kontraposisi

p q p q p  q pq

Invers

q  p Konvers

qp Kontraposisi

B B S S B B B B

B S S B S B B S

S B B S B S S B

S S B B B B B B

Dari implikasi p  q di atas, dapat dibentuk tiga implikasi lain yaitu a. Konversnya, yaitu q  p (kolom 7, pada tabel 2.9)

b. Inversnya, yaitu ~p  ~q atau ditulis pq (kolom 6, pada tabel 2.9) c. Kontraposisinya, yaitu ~q  ~p atau ditulis qp(kolom 8, pada tabel 2.9) Catatan:

1. Kolom ke-5 (implikasi p  q) mempunyai nilai logika yang sama dengan kolom ke- 8 (kontraposisinya, qp ).

Dinyatakan dengan p  q  qp

Dibaca: implikasi p  q ekivalen dengan qp

2. Kolom ke-6 (Invers, pq) mempunyai nilai logika yang sama dengan kolom ke-7 (Konversi, q  p ).

Dinyatakan dengan pq  q  p.

Dibaca implikasi pq ekivalen dengan q  p.

Contoh (2. 12)

Implikasi: Jika hati tenang maka kita senang.

Konvers: Jika kita senang maka hati tenang.

Invers: jika hati tidak tenang maka kita tidak senang

Kontraposisi: Jika kita tidak senang maka hati tidak tenang.

Contoh (2.13)

Implikasi: Jika suatu bendera adalah bendera Republik Indonesia maka benderanya ada warna merahnya

______________________________________________

Konvers: Jika benderanya ada warna merahnya maka bendera tersebut adalah bendera RI. q  p

Invers: Jika suatu bendera bukan bendera RI maka benderanya tidak ada warna merahnya

Kontraposisi: Jika suatu bendera tidak ada warna merahnya maka bendera tersebut bukan bendera RI.

2.5.6. Bi-Implikasi (pernyataan bersyarat dua arah)

Bi-implikasi adalah pernyataan majemuk yang terbentuk dari dua pernyataan tunggal yang dirangkai menggunakan operator logika “ jika dan hanya jika” dengan symbol “  “ . Operator logika tersebut menunjukan bahwa pernyataan biimplikasi merupakan pernyataan bersyarat dua arah

Misalkan dua pernyataan p dan q diberi operator logika “ jika dan hanya jika’, dapat ditulis “p  q” disebut bi-implikasi dan dibaca “p jika dan hanya jika q”. Ada beberapa ucapan Bi-Implikasi p  q lainya

1. p bila dan hanya bila q

2. jika p maka q, dan jika q maka p 3. p ekivalen dengan q

4. p merupakansyarat perlu dan cukup bagi q

Bi-implikasi menunjukan hubungan keterkaitan antara p dan q. Pada bi-implikasi “p

 q” berarti p adalah syarat perlu dan syarat cukup bagi q dan begitu sebaliknya q adalah syarat perlu dan syarat cukup bagi p.

Karena implikasi berlaku dua arah (bersyarat ganda), maka bi-implikasi akan bernilai benar jika nilai kebenaran kedua pernyataannya sama. Dengan tabel nilai kebenaran sebagai berikut:

Tabel 2.10. Tabel nilai kebenaran Bi - Implikasi

Untuk membedakan pernyataan implikasi dan bi-implikasi, perhatikan contoh berikut:

1. Jika seseorang masih hidup, maka ia masih bernafas 2. Jika hari ini hujan, maka jalanan akan licin

Pembahasan:

Dari contoh (1) pernyataan “Jika seseorang masih hidup, maka ia masih bernafas”

Pernyataan tersebut dikenal sebagai implikasi. Dan pernyataan tersebut bisa diubah menjadi bi-implikasi yaitu “Seseorang masih hidup, jika dan hanya jika ia masih bernafas”

Atau “seseorang masih bernafas, jika dan hanya jika ia masih hidup”

Dalam hal ini bernafas dan hidup sama-sama dapat bertindak sebagai sebab dan sekaligus akibat

Dari contoh (2) pernyataan “Jika hari ini hujan, maka jalanan akan licin” Pernyataan ini juga dikenal sebagai implikasi dan tidak berlaku syarat ganda.

p q p  q Dibaca

B B B Jika p benar jika dan hanya jika q benar maka p  q benar B S S Jika p benar jika dan hanya jika q salah maka p  q salah S B S Jika p salah jika dan hanya jika q benar maka p  q salah S S B Jika p salah jika dan hanya jika q salah maka p  q benar

Jika hari ini hujan, maka jalanan akan licin, tetapi jika jalanan licin belum tentu hari ini hujan, artinya masih ada kemungkinan lain yang dapat menyebabkan jalanan licin, dalam hal ini hujan adalah sebab dan licin adalah akibat

Di bawah ini diberikan diagram Venn untuk Bi-implikasi

Gambar: 2.5 Diagram venn untuk Bi-implikasi

Jika p(x) q(x) merupakan bi-implikasi logis, maka tiap-tiap penggantian nilai x yang menyebabkan kalimat p(x) bernilai benar akan menyebabkan q(x) juga bernilai benar. Begitu sebaliknya tiap-tiap penggantian nilai x yang menyebabkan kalimat q(x) bernilai benar akan menyebabkan p(x) juga benar

Jika P dan Q adalah himpunan penyelesaian dari kalimat p(x) dan q(x), maka p(x) q(x) akan bernilai benar jika P = Q

Contoh (2.14):

1. 20 + 7 = 27 jika dan hanya jika 27 bukan bilangan prima 2. 2 bilangan genap jika dan hanya jika 3 bilangan ganjil 3. 2 + 2 ≠ 5 jika dan hanya jika: 4 + 4 < 8

4. Surabaya ada di jawa barat jika dan hanya jika 2³ = 6 Pembahasan

(1). Misal: p : 20 + 7 = 27 (bernilai benar)

q : 27 bukan bilangan prima (bernilai benar)

Maka pernyataan: 20 + 7 = 27 jika dan hanya jika 27 bukan bilangan prima dinyatakan sebagai p  q akan bernilai benar.

(2). Misal: p : 2 bilangan ganjil (bernilai salah) q : 3 bilangan ganjil (bernilai benar)

Maka pernyataan: 2 bilangan genap jika dan hanya jika 3 bilangan ganjil dinyatakan sebagai p  q akan bernilai salah.

(3). Misal: p : 2 + 2 ≠ 5 (bernilai benar) dan q : 4 + 4 < 8 (bernilai salah)

Maka pernyataan: 2 + 2 ≠ 5 jika dan hanya jika: 4 + 4 < 8 dinyatakan sebagai p  q akan bernilai salah

(4). Misal: p : Surabaya ada di jawa barat (bernilai salah) q : 2³ = 6 (bernilai salah)

Maka pernyataan: Surabaya ada di jawa barat jika dan hanya jika 2³ = 6 dinyatakan sebagai p  q akan bernilai benar

S P = Q

P  Q benar, jika P = Q

______________________________________________

2.6. Urut-urutan Penggunaan Kata Hubung Kalimat.

Dalam penggunaan tata bahasa sehari-hari kita sering menjumpai pernyataan yang menggunakan banyak kata hubung kalimat (operator logika), seperti misalnya:

“Saya akan berjalan kaki atau naik sepeda maka saya tidak akan terlambat kuliah”.

Kalimat diatas, akan ditafsirkan begini:

”Jika saya berjalan kaki atau naik sepeda, saya tidak akan terlambat mengikuti kuliah”.

Ada juga yang menafsirkan:

“Saya berjalan kaki atau, jika saya naik sepeda maka saya tidak akan terlambat kuliah”.

Untuk dapat mengerti pernyataan komposit (pernyataan yang memuat 5 operator logika) diatas dengan benar diperlukan kejelasan berbahasa dengan menggunakan tanda- tanda baca yang diperlukan, misalnya: koma, dengan demikian kita dapat menterjemahkan pernyataan diatas ke pernyataan simbolik dengan benar. Demikian pula halnya dengan pernyataan simbolik yang kita gunakan. Pernyataan ini harus jelas sehingga tidak menimbulkan salah tafsir.

Penggunaan tanda kurung untuk menunjukkan urutan pengerjaan. Tetapi untuk pernyataan yang banyak menggunakan kata hubung kalimat, penggunaan tanda kurung dirasakan kurang effisien. Untuk itu dalam logika matematika penggunaan urut-urutan pengerjaan adalah sebagai berikut:

1. negasi

2. konjungsi, disjungsi 3. kondisional

4. bikondisional Contoh (2.15):

1. ~ p ∨ q berarti (~ p) ∨ q merupaka kalimat disjungtif dengan negasi diselesaikan terlebih dahulu.

2. p ∧ q  r berarti (p ∧ q)  r merupakan kalimat kondisional dengan tanda kurung dikerjakan lebih dahulu

3. p  q  r berarti p  (q  r) merupakan kalimat bikondisional dengan implikasi yang di tanda kurung diselesaikan terlebih dahulu

2.7. Negasi (Ingkaran dari kalimat)

Penggunaan simbol “” dibaca ekivalen atau ekuivalen logis (secara logika mempunyai nilai kebenaran yang sama). Di bawah ini diberikan beberapa ingkaran- ingkaran baku yaitu:

2.7.1 Ingkaran dari konjungsi

Jika konjungsi dari pernyataan p dan q ditulis dengan p ∧ q maka negasi (ingkaran) dari konjungsi tersebut dapat dituliskan sebagai ~ (p ∧ q) atau ditulis ^p^q , dengan nilai kebenarannya dapat disajikan dalam tabel 2.11 berikut ini:

Tabel 2.11 Tabel ingkaran dari konjungsi

Dari tabel 2.11 diperoleh ingkaran dari konjungsi p ∧ q ditulis ~ (p ∧ q) ~ p  ~ q (notasi dibaca ekuivalen, sama)

Contoh (2.16)

Tentukan ingkaran dari pernyataan berikut

a) Kaizen berambut keriting dan berhidung mancung b) Tiga adalah bilangan prima dan bilangan ganjil c) 27 – 22 = 5 dan log 100 = 2

d) Sebelas adalah bilangan genap dan delapan habis dibagi dua Pembahasan (ingkarannya):

a) Kaizen tidak berambut keriting atau tidak berhidung mancung b) Tiga bukan bilangan prima atau bukan bilangan ganjil

c) 27 – 22 tidak sama dengan 5 atau log 100 tidak sama dengan 2 d) Sebelas bukan bilangan genap atau delapan tidak habis dibagi dua 2.7.2 Ingkaran dari Disjungsi

Jika disjungsi dari pernyataan p dan q ditulis dengan p  q maka negasi (ingkaran) dari disjungsi tersebut dapat dituliskan sebagai ~ (p  q) atau ditulis pq , dengan nilai kebenarannya dapat disajikan dalam tabel 2.12 di bawah ini:

Dari tabel 2.12 diperoleh ingkaran dari disjungsi p  q ditulis ~ (p  q) ~ p ∧ ~ q (notasi dibaca ekuivalen, sama)

Tabel 2.12 Tabel ingkaran dari disjungsi

Contoh (2.17)

Tentukan ingkaran dari pernyataan berikut

a) Exa anak yang rajin belajar atau suka olah raga b) Aisya anak yang cantik atau sholeh

c) Niken hobi membaca atau menulis

d) Sembilan adalah bilangan prima atau ganjil Pembahasan (ingkarannya):

a) Exa bukan anak yang rajin belajar dan tidak suka olah raga

p q ~ p ~ q p  q ~ (p ∧ q) ~ p  ~ q

B B S S B S S

B S S B S B B

S B B S S B B

S S B B S B B

p q ~ p ~ q p  q ~ (p  q) ~ p ∧ ~ q

B B S S B S S

B S S B B S S

S B B S B S S

S S B B S B B

______________________________________________

c) Niken tidak hobi membaca dan tidak hobi menulis d) Sembilan bukan bilangan prima dan bukan ganjil 2.7.3 Ingkaran dari Ingkaran

Jika ingkaran dari pernyataan p dituliskan sebagai ~ p atau p , maka ingkaran dari ingkaran ~ p ditulis sebagai ~ (~p ) atau p , dengan nilai kebenarannya dapat disajikan dalam tabel 2.13 berikut ini:

Tabel 2.13 Tabel ingkaran dari ingkaran

Dari tabel 2.13 dapat diperoleh bahwa ingkaran dari ingkaran adalah ~ (~p )  p atau p  p (kolom pertama sama dengan kolom ke tiga)

Contoh (2.18)

Tentukan ingkaran dari ingkaran berikut a) Pulau Bali dikenal sebagai pulau Dewata b) 625 adalah bilangan kuadrat

c) 4 adalah faktor dari 12

d) Dua garis yang sejajar mempunyai titik potong Pembahasan (ingkarannya):

a) Misal: p: Pulau Bali dikenal sebagai pulau Dewata ~p: Pulau Bali tidak dikenal sebagai pulau Dewata

Maka: ~ (~p): Pulau Bali tidak tidak dikenal sebagai pulau Dewata  Pulau Bali dikenal sebagai pulau Dewata

Jadi p  p

b) Misal p: 625 adalah bilangan kuadrat ~p: 625 bukan bilangan kuadrat

Maka: ~ (~p): 625 bukan bukan bilangan kuadrat  625 adalah bilangan kuadrat Jadi p  p

c) Misal: p: 4 adalah faktor dari 12 ~p : 4 bukan faktor dari 12

Maka: ~ (~p ): 4 bukan bukan faktor dari 12  4 adalah faktor dari 12 Jadi p  p

d) Misal: p: Dua garis yang sejajar mempunyai titik potong ~p: Dua garis yang sejajar tidak mempunyai titik potong

Maka: ~ (~p ): Dua garis yang sejajar tidak tidak mempunyai titik potong.

 Dua garis yang sejajar mempunyai titik potong Jadi p  p

p ~ p ~ (~p ) , ditulis p

B S B

S B S

2.7.4 Ingkaran dari Implikasi

Jika implikasi dari pernyataan p dan q ditulis dengan p  q maka negasi (ingkaran) dari implikasi tersebut dapat dituliskan sebagai ~ (p  q) atau ditulis pq , dengan nilai kebenarannya dapat disajikan dalam tabel 2.14 berikut ini:

Tabel 2.14 Tabel ingkaran dari implikasi

Dari tabel 2.14 diperoleh ingkaran dari implikasi p  q ditulis ~ (p  q)  p ∧ ~ q atau pq  pq (notasi dibaca ekuivalen, sama)

Contoh (2.19 )

Tentukan ingkaran dari pernyataan berikut

a) Jika 9 adalah bilangan ganjil, maka 8 adalah bilangan genap b) Jika 10 = 1, maka log 20 = 2

c) Jika 5 hanya habis dibagi 1 dan 5, maka 5 adalah bilangan prima d) Jika x = 3, maka x² = 9

Pembahasan (ingkarannya):

a) 9 adalah bilangan ganjil, dan 8 bukan bilangan genap b) 10 = 1, dan log 20



²

c) 5 hanya habis dibagi 1 dan 5, dan 5 bukan bilangan prima d) x = 3, dan x²



⁹

2.7.4 Ingkaran dari Bi-implikasi

Jika bi-implikasi dari pernyataan p dan q ditulis dengan p  q maka negasi (ingkaran) dari bi-implikasi tersebut dituliskan sebagai ~ (p  q) atau ditulis pq , dengan nilai kebenarannya dapat disajikan dalam tabel 2.15 berikut ini:

Tabel 2.15 Tabel ingkaran dari disjungsi

Dari tabel 2.15 diperoleh ingkaran dari bi-implikasi p  q ditulis ~ (p  q) pada kolom 6 nilai kebenarannya sama dengan (ekuivalen) dengan ( p ∧ ~ q)  (~ p ∧ q ) pada kolom 9 dan ditulis dengan ~ (p  q)  ( p ∧ ~ q)  (~ p ∧ q ) (notasi dibaca, sama).

Atau dapat juga diberi notasi p q (pq)(pq)

p q ~ q p  q ~ ( p  q ) p ∧ ~ q

B B S B S S

B S B S B B

S B S B S S

S S B B S S

p q ~ p ~ q p  q ~ ( p  q ) p ∧~ q ~ p ∧ q ( p ∧ ~ q)  (~ p ∧ q )

B B S S B S S S S

B S S B S B B S B

S B B S S B S B B

S S B B B S S S S