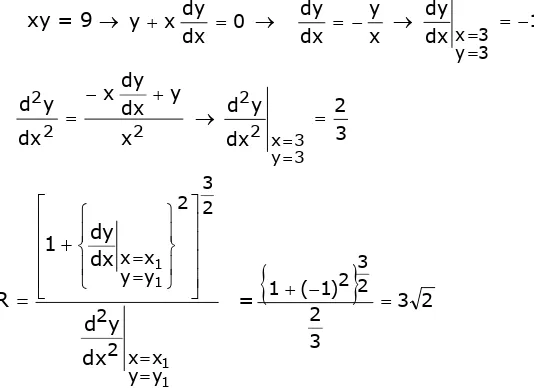kalkuls bab v penerapan diferensiasi

(1)

BAB V

PENERAPAN DIFFERENSIASI

5.1 Persamaan garis singgung

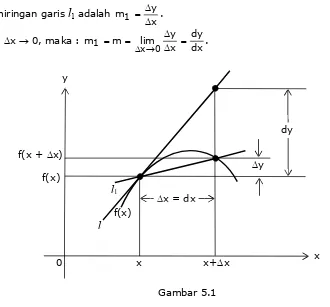
Bentuk umum persamaan garis adalah y = mx + n, dimana m adalah koeffisien arah atau kemiringan garis dan n adalah penggal garis. Sekarang perhatikan Gambar 5.1.

Kemiringan garis

l

₁_adalah

x y m₁

D D = .

Jika Dx ® 0, maka :

dx dy x y lim m m

0 x

1 = = _DD =

® D

.

Jadi dapat disimpulkan bahwa kemiringan garis yang menyinggung titik (x,y) pada f(x) adalah :

) x ( ' f dx dy

m= = (5.1)

Jika garis tersebut menyinggung titik P(x1,y1) maka kemiringannya adalah : )

x ( ' f dx

dy

m ₁

x x ₁

= =

=

(5.2)

Contoh 5.1

Tentukan persamaan garis yang menyinggung kurva y = x2_{+ x -3 di titik P(2,3)} Penyelesaian :

Dx = dx

l

₁

f(x)

l

f(x + Dx)

f(x)

Dy dy y

x x+Dx x 0

(2)

y = x2 + x -3 ® 2x 1 dx

dy

+ =

Kemiringan garis singgung yang menyinggung titik P(2,3) adalah :

5

Persamaan garis : y = mx + n. Karena menyinggung titik P(2,3) maka : 3 = 5(2) + n ® n = -7.

Jadi garis singgung yang menyinggung titik P(2,3) adalah : y = 5x – 7

5.2 Persamaan garis normal

Garis normal adalah garis yang tegak lurus terhadap garis singgung. Dari pembahasan terdahulu kita telah mengetahui bahwa dua garis dikatakan saling tegak lurus jika perkalian kemiringan garisnya sama dengan -1; atau dalam bentuk rumus dapat ditulis menjadi :

m1.m2 = -1 atau

Tentukan persamaan garis singgung dan garis normal di titik (1,6) pada kurva : y = 3x2_–_{2x + 5}

Penyelesaian :

2

Jika diketahui persamaan parameter

t garis singgung, garis normal dan titik singgung pada t = 2.

Penyelesaian :

Titik singgung untuk t = 2 adalah (-2,12)

(3)

Jadi persamaan : garis singgung : y = 12x + 36

garis normal : y =

6 71 x 12

1 +

-

Soal-soal

1.Tentukan persamaan garis singgung dan garis normal dari kurva :

a) x 1

2 1

y= - 2 + di titik ) 2 1 , 1 (

b) x2– xy2 + 3y2 = 13 di titik P(2,3)

2. Tentukan persamaan garis singgung, garis normal dan titik singgung dari fungsi parameter :

1 t titik di

1 t

1 t y

1 t

t x

2

=

ï ï î ï ï í ì

+ -=

+ =

5.3 Kelengkungan (Curvature)

Besarnya kelengkungan suatu kurva di titik tertentu dipengaruhi seberapa cepatnya perubahan arah dari kurva di titik tersebut. Jika perubahan arah suatu kurva di titik tertentu terjadi secara berangsur-angsur maka harga kelengkungannya besar. Sebaliknya jika perubahan arah kurva terjadi secara mendadak maka kelengkungannya kecil.

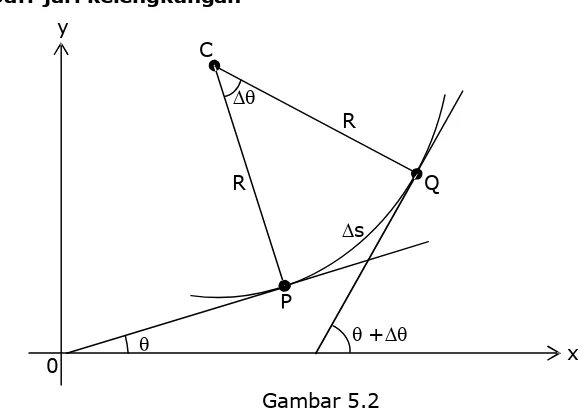
5.3.1 Jari-jari kelengkungan

Pada Gambar 5.2 dapat dilihat bahwa garis normal CP dan CQ berpotongan di titik C. Panjang busur PQ = Ds. Jika jarak titik P dan titik Q sangat kecil, maka CP = CQ = R dan panjang busur Ds ® 0. Telah

q q +Dq

R Q

Ds

P y

x 0

Gambar 5.2 C

Dq

(4)

diketahui bahwa panjang busur suatu lingkaran yang dibatasi oleh sudut q adalah Rq. Sehingga panjang busur :

PQ = Ds = R.Dq atau

Perhatikan Gambar 5.3

Jika Ds ® 0 maka =tanq

Jadi jari-jari kelengkungan di titik (x,y) adalah :

2

Sedangkan jari-jari kelengkungan di titik (x1,y1) adalah :

(5)

Contoh 5.4

Tentukan jari-jari kelengkungan dari hiperbola xy = 9 di titik (3,3) Penyelesaian :

xy = 9 ® 0

5.3.2 Pusat kelengkungan ( Center of Curvature )

(6)

k = y1 + LC Sehingga :

h = x1– R sin q

( 5. 7 )

k = y1 + R cos q Contoh 5.5

Tentukan pusat kelengkungan dari kurva pada contoh 5.4 Penyelesaian :

x1 = 3 ; y1 = 3 ; R = 3 2 ;

x y dx dy

-= ( didapat dari contoh 5.4 )

tan q = 1 dx

dy

3 y 3 x =

-=

= ®q = 4

p

- radian ; sin

)

1 /

2

4 (

-

p

=

-

;

cos

)

1 /

2

4 (

-

p

=

h = 3 – (3 2)(-1/2 ) = 3 + 3 = 6; k = 3 + (3 2)(1/2 ) = 3 + 3 = 6 Jadi pusat kelengkungan adalah : C(6, 6)

Soal-soal

1. Tentukan jari-jari kelengkungan dan pusat kelengkungan untuk kurva : a) y = x2_{+ xy}_–_{24 di titik (1,-2)}

b) 1

16 y 25 x2 2

=

+ di titik (1,4)

c) y2 = - x2 +4x – 3 di titik (1,2)

2. Tentukan jari-jari dan pusat kelengkungan dari fungsi parametrik :

4 pada tan 2 y

sec 3

x p

= q

î í ì

q =

5.4 Nilai ekstrim

Misal terdapat suatu hasil pengukuran seperti yang ditunjukkan pada Gambar 5.5. Pengukuran tersebut dapat berupa pengukuran temperatur, tekanan atau pertumbuhan suatu jenis bakteri terhadap waktu atau pengukuran lainnya. Jika

(7)

kita perhatikan Gambar 5.5, harga pengukuran meningkat pada [x0,x1], menurun pada [x1,x2] dan seterusnya hingga konstan pada selang [x6,x7].

Definisi 5.4.1

Misal suatu fungsi terdefinisi pada selang I. Jika x1 dan x2 adalah dua buah bilangan yang terletak pada selang I, maka :

i) fungsi f naik pada selang I, jika x1 < x2 menghasilkan f(x1) < f(x2) ii) fungsi f turun pada selang I, jika x1 < x2 menghasilkan f(x1) > f(x2) iii) fungsi f konstan selang I jika f(x1) = f(x2) untuk setiap harga x1 dan x2 Teorema 5.4.2

Jika suatu f kontinu pada selang tertutup [a,b] maka f setidak-tidaknya mempunyai satu nilai maksimum dan minimum [a,b].

Contoh 5.6

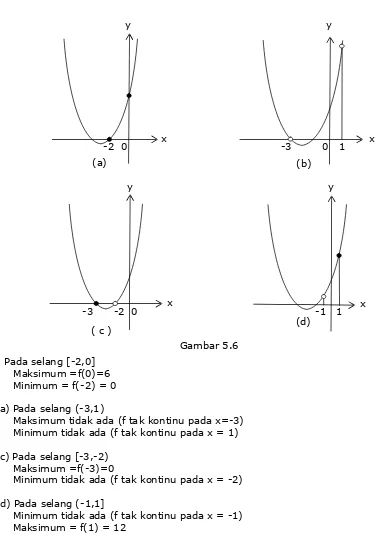
Jika diketahui f(x) = x2_{+ 5x + 6, tentukan nilai ekstrim f untuk selang-selang} berikut : a) [-2,0] b) (-3, 1) c) [-3,-2) d) (-1,1]

Penyelesaian :

0 x0 = a x1 x2 x3 x4 x5 x6 x7

x y

(8)

Pada selang [-2,0]

Maksimum =f(0)=6 Minimum = f(-2) = 0

a)Pada selang (-3,1)

Maksimum tidak ada (f tak kontinu pada x=-3) Minimum tidak ada (f tak kontinu pada x = 1)

c) Pada selang [-3,-2) Maksimum =f(-3)=0

Minimum tidak ada (f tak kontinu pada x = -2)

d) Pada selang (-1,1]

Minimum tidak ada (f tak kontinu pada x = -1) Maksimum = f(1) = 12

5.4.1 Nilai Ekstrim Lokal

Istilah nilai ekstrim lokal sering digunakan apabila terdapat suatu selang terbuka yang mengandung bilangan c sedemikian rupa sehingga f mempunyai nilai terbesar (maksimum) atau terkecil (minimum). Setiap harga f yang mempunyai harga maksimum atau minimum disebut ekstrim

(b)

( c ) (d)

-3 -2 0 -1 1

x x

y y y y

-2 0 -3 0 1 (a)

(9)

Definisi 5.4.3

Jika c adlah bilangan yang terletak dalam daerah definisi (domain) fungsi, maka :

i) f(c) adalah maksimum lokal f jika terdapat suatu selang terbuka (a,b) yang mengandung c sedemikian rupa sehingga f(x) £ f(c) untuk setiap x pada (a,b).

ii) f(c) adalah minimum lokal f jika terdapat suatu selang terbuka (a,b) yang mengandung c sedemikian rupa sehingga f(x) ³ f(c) untuk setiap x pada (a,b).

Teorema 5.4.4

Misal c adalah bilangan yang terletak pada selang terbuka (a,b). Suatu fungsi f dikatakan mempunyai ekstrim lokal pada titik c jika f’(c) = 0.

Teorema 5.4.5

Misal c adalah bilangan yang terletak pada selang terbuka (a,b). Suatu fungsi f dikatakan tidak mempunyai ekstrim lokal pada titik c jika f’(c) ada dan tidak sama dengan 0.

Teorema 5.4.6

Misal c adalah bilangan yang terletak pada selang tertutup [a,b]. Suatu fungsi f dikatakan mempunyai ekstrim lokal pada titik c jika f’(c) = 0.

Teorema 5.4.7

Jika c merupakan daerah definisi dan merupakan bilangan kritis f, maka f’(c) = 0.

5.4.2 Nilai Ekstrim Mutlak

Jika f(c) adalah nilai maksimum mutlak dari fungsi f, maka kita dapat menyimpulkan bahwa titik (c, f(c)) merupakan titik tertinggi pada garafik f. Sebaliknya f(c) adalah minimum mutlak dari fungsi f, maka titik (c,f(c)) merupakan titik terendah pada grafik f. Nilai maksimum dan/atau minimum sering disebut juga dengan nilai ekstrim fungsi f.

Teorema 5.4.8

Misal fungsi f terdefinisi pada suatu himpunan bilangan ril S. Jika c terletak pada S, maka :

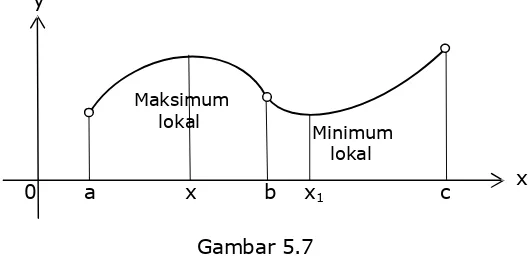
0 a x b x1 c x y

Gambar 5.7 Maksimum

lokal

(10)

i) f(c) adalah nilai maksimum mutlak f jika f(x) £ f(c) untuk setiap nilai x yang terletak dalam S.

ii) f(c) adalah nilai minimum mutlak f jika f(x) £ f(c) untuk setiap nilai x yang terletak dalam S.

Tuntunan untuk medapatkan nilai-nilai ekstrim fungsi f yang kontinu pada selang tertutup [a,b] :

1. Tentukan seluruh nilai kritis f pada selang terbuka (a,b) 2. Tentukan titik ujung

a) Jika fungsi f terletak pada selang tertutup [a,b] maka titik ujungnya adalah a dan b.

b) Jika fungsi f terletak pada selang terbuka (a,b) maka f tidak mempunyai titik ujung.

c) Jika fungsi f terletak pada selang setengah terbuka (a,b] maka titik ujungnya adalah b.

d) Jika fungsi f terletak pada selang setengah terbuka [a,b) maka titik ujungnya adalah a.

3. Hitung nilai f(c) untuk setiap bilangan kritis c yang didapat dari nomor 1 diatas.

4. Hitung harga f pada setiap titik ujung.

5. Nilai maksimum dan minimum dari fungsi f adalah nilai terbesar dan terkecil yang dihitung pada nomor 3 dan 4 diatas.

Tuntunan untuk medapatkan nilai-nilai ekstrim fungsi f yang kontinu pada selang terbuka (a,b) :

1.Tentukan seluruh nilai kritis f pada selang terbuka (a,b). 2.Hitung nilai f(c) untuk seluruh nilai kritis.

3. Nilai maksimum dan minimum dari fungsi f adalah nilai terbesar dan terkecil yang dihitung pada nomor 2 diatas.

Tuntunan untuk mendapatkan nilai-nilai ekstrim fungsi f yang kontinu pada selang setengah terbuka [a,b) :

3. Hitung nilai f(a)

Tuntunan untuk medapatkan nilai-nilai ekstrim fungsi f yang kontinu pada selang setengah terbuka (a,b] :

3. Hitung nilai f(b)

Contoh 5.7

Jika diketahui f(x) = 2x3 - 3x2– 12x + 10, tentukan nilai maksimum dan minimum f pada selang tertutup [-4,3]

Penyelesaian :

(11)

6x2_–_6x_–_{12 = 0}_®_6(x2_–_x_–_{2) = 0}_®_{6(x-2)(x+1) = 0} x1 = 2 ; x2 = -1

f(x1) = f(2) = 16 – 12 – 24 + 10 = -10 f(x2) = f(-1) = -2 – 3 + 12 + 10 = 17 Titik ujung : -4 dan 3

f(-4) = -64 – 48 + 48 + 10 = -54 f(3) = 54 – 27 -36 + 10 = 1 Jadi : f(2) adalah minimum lokal

f(-1) adalah maksimum lokal dan maksimum mutlak f(-4) adalah minimum mutlak

Soal-soal

1.Tentukan nilai-nilai ekstrim dari fungsi berikut ini serta gambarkan grafiknya !

a) f(x) = x 2x 2

1 ₂

- ; [2,5] c) f(x) = 3x2 -10x+7 ; [-1,3)

b) f(x) = 5-6x2-2x3 ; (-3,1] d) f(x) = x4 -5x2 +4 ; (-2,2)

2.Tentukan nilai-nilai kritis dari fungsi-fungsi berikut ini ! a) f(x) = 4x2 -3x+2 c) f(x) = 2x3 -x2 -20x+4

b) f(x) = 2x + 5 d) f(x) = 4x3+5x2-42x+7

5.5 Kecekungan dan kecembungan

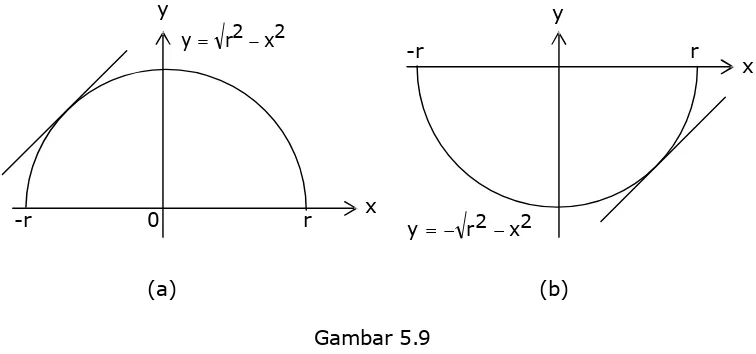
Jika terdapat sebuah persamaan lingkaran x2 + y2 = r2, maka persamaan tersebut dapat ditulis menjadi :

2 x 2 r ) x ( f

y=± =± -atau :

2 x 2 r ) 1 x (

f = - atau f(x₂)=- r2-x2 -4 -3 -2 -1 1 2 3

0 x

Gambar 5.8 y

(12)

Jika kita perhatikan Gambar 5.7 (a) maka akan terlihat bahwa garis singgung yang menyinggung kurva pada sembarang titik selalu berada pada bagian atas kurva pada selang terbuka (-r,r). Sedangkan pada Gambar 5.7 (b) garis singgung yang menyinggung kurva selalu berada bagian bawah kurva pada selang terbuka (-r,r). Bentuk Gambar 5.7 (a) biasanya disebut cembung keatas atau cekung kebawah dan Gambar 5.7 (b) biasanya disebut cembung kebawah atau cekung keatas.

Definisi 5.5.1

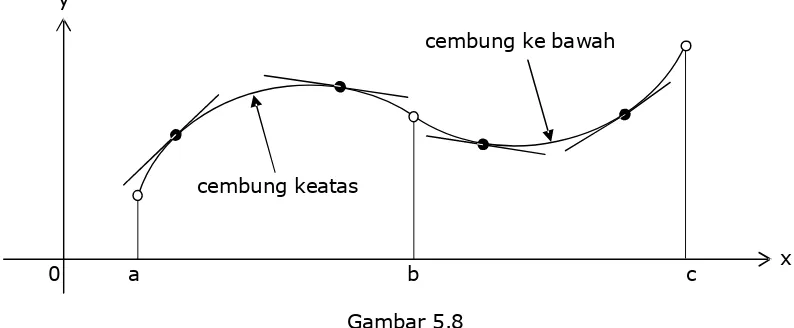
Kurva f dikatakan cembung ke bawah (cekung keatas) pada selang (a,b) jika garis singgung yang menyinggung kurva pada sembarang titik pada selang (a,b) selalu terletak pada bagian bawah kurva f. Sebaliknya kurva f dikatakan cembung keatas (cekung kebawah) jika garis singgung yang menyinggung kurva pada sembarang titik pada selang (a,b) selalu terletak pada bagian atas kurva f.

Kurva f pada Gambar 5.8 cembung keatas pada selang (a,b) dan cembung kebawah pada selang (b,c).

y _y

x

x -r r

-r 0 r _y₌_- _r2_-_x2 2

x 2 r y=

-Gambar 5.9

(13)

Definisi 5.5.2

Jika pada selang (a,b) terdapat sembarang bilangan ril xo dan harga turunan kedua f pada x = xo atau f’’(xo) < 0 maka kurva f pada selang tersebut cekung kebawah atau cembung keatas. Jika pada selang (a,b) harga f’’(xo) > 0, maka kurva f pada selang tersebut cekung keatas atau cembung kebawah.

Definisi 5.5.3

Misal kurva f mempunyai persamaan y = f(x) dan kontinu di titik x = xo. Jika f’’(xo) = 0 dan disekitar x = xo berlaku f’’(x)>0 untuk x<xo dan f’’(x) < 0 untuk x>xo atau berlaku f’’(x)<0 untuk x<xo dan f’’(x) > 0 untuk x>xo, maka titik (xo,f(xo)) merupakan titik belok dari kurva tersebut.

Contoh 5.8

Tentukan daerah cembung keatas dan cembung kebawah jika diketahui : f(x) = 6 – 5x + x2.

Penyelesaian :

f(x) = 6 – 5x + x2 ; f’(x) = -5 + 2x ; f’’(x) = 2

Karena f’’(x) > 0 untuk sembarang bilangan ril xo, maka kurva f cembung kebawah.

Contoh 5.9

Jika diketahui persamaan f(x) = 2+x+3x2_-x3_{, tentukan daerah pada kurva f} yang merupakan daerah cembung kebawah, daerah cembung keatas dan titik belok dari kurva yang dimaksud !

Penyelesaian : f(x) = 2+x+3x2-x3

f’(x) = 1 + 6x – 3x2 f’’(x) = 6 – 6x

Daerah cembung keatas :

f’’(x) = 6 – 6x < 0 ® x>1

Daerah cembung kebawah : f’’(x) = 6 – 6x > 0 ® x<1

Titik belok :

f’’(x) = 6 – 6x = 0 ® x=1 Soal-soal

cembung keatas

cembung ke bawah y

x 0 a b c

(14)

Tentukan daerah cembung kebawah, cembung keatas dan titik belok kurva dari fungsi berikut jika ada !

1. f(x) = x3_–_{x + 2} _{6. f(x) = 2x +(3x+1)}3/5

5.6 Kecepatan dan percepatan sesaat 5.6.1 Kecepatan

Sebelum kita membahas kecepatan dan percepatan sesaat, kiranya kita perlu mengetahui apa yang dimaksud dengan kecepatan dan percepatan rata-rata. Kecepatan rata-rata (v)pada bidang datar didefinisikan sebagai

t menentukan kecepatan rata-rata saja; tidak dapat digunakan untuk menghitung kecepatan untuk suatu saat tertentu. Sebetulnya persamaan 5.8 dapat digunakan untuk menentukan kecepatan untuk suatu saat tertentu, dengan catatan Dt sangat kecil atau dalam bentuk rumus :

dt

dimana v adalah kecepatan sesaat dan ds/dt adalah turunan pertama dari lintasan. Lintasan (s) adalah fungsi waktu atau dapat ditulis dalam bentuk s = s(t).

5.6.2 Percepatan

Percepatan rata-rata (a)pada bidang datar didefinisikan sebagai

(15)

2 dt

s 2 d dt dv a t v

0 t lim a 0 t

lim ® = =

D D ® D = ® D

( 5.11 )

dimana a adalah kecepatan sesaat dan dv/dt adalah turunan pertama dari kecepatan.

Contoh 5.10

Lintasan sebuah partikel ditunjukkan oleh persamaan s = 3t2 _–_{5t + 2,} dimana t dalam detik dan s dalam satuan meter. Tentukan panjang lintasan, kecepatan dan percepatan pada saat t = 15 detik.

Penyelesaian : s = t(3t – 5)

5 t 6 v dt ds

-= =

6 a dt dv 2 dt

s 2 d

= = =

Untuk t = 15 detik :

Didapat : s = 15(45-5) = 600 meter v = 90 – 5 = 85 m/detik a = 6 m/detik2

Soal

Berikut adalah lintasan partikel yang bergerak dengan percepatan konstan. Tentukan panjang lintasan dan kecepatan partikel pada waktu t = 50 detik !

0 10 15 240

110 s (meter)