MAKALAH MAKALAH
PERSAMAAN DAN PERTIDAKSAMAAN LOGARITMA PERSAMAAN DAN PERTIDAKSAMAAN LOGARITMA
Diajukan untuk me
Diajukan untuk memenuhi salah menuhi salah satu tugas mata kuliasatu tugas mata kuliah Kapikta Selekta h Kapikta Selekta SMA 1SMA 1 Dosen Pengampu : Drs.H . Zaenal Saeful, M.Pd
Dosen Pengampu : Drs.H . Zaenal Saeful, M.Pd : Ehda Farlina, M.Pd : Ehda Farlina, M.Pd Oleh: Oleh: Kelompok 11 Kelompok 11 1. 1. Sunarli Sunarli (1122050073)(1122050073) 2.
2. Ahmad Ahmad Ruslan Ruslan (1132050002)(1132050002) 3.
3. Asry Asry Erma Erma Yunita Yunita (1132050009)(1132050009) 4.
4. Ayuni Ayuni Khairiyyah Khairiyyah (1132050011)(1132050011) 5.
5. Desi Desi Ratnasari Ratnasari (1132050015)(1132050015)
PRODI PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MIPA PRODI PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MIPA
FAKULTAS TARBIYAH DAN KEGURUAN FAKULTAS TARBIYAH DAN KEGURUAN
UNIVERSITAS ISLAM NEGERI UNIVERSITAS ISLAM NEGERI
SUNAN GUNUNG DJATI SUNAN GUNUNG DJATI
BANDUNG BANDUNG
2016 2016
KATA PENGANTAR KATA PENGANTAR
Bismillahirrahmanirrahim Bismillahirrahmanirrahim
Puji syukur kami panjatkan kehadirat Allah SWT. atas rahmat dan karunia-Nya Puji syukur kami panjatkan kehadirat Allah SWT. atas rahmat dan karunia-Nya kami dapat menyusun makalah ini. Makalah ini membahas tentang persamaan dan kami dapat menyusun makalah ini. Makalah ini membahas tentang persamaan dan pertidaksam
pertidaksamaan logaritmaan logaritma beserta pea beserta penyelesaiannynyelesaiannya.a.
Tak lupa kami mengucapkan terima kasih kepada berbagai pihak yang telah membantu Tak lupa kami mengucapkan terima kasih kepada berbagai pihak yang telah membantu kami dalam penyusunan makalah ini. Diantaranya:
kami dalam penyusunan makalah ini. Diantaranya: 1.
1. Bapak Drs.H . Zaenal Saeful, M.Pd , selaku dosen mata kuliah PembelajaranBapak Drs.H . Zaenal Saeful, M.Pd , selaku dosen mata kuliah Pembelajaran Matematika SMA/MA 1
Matematika SMA/MA 1 2.
2. Seluruh pihak yang tidak dapat kami sebutkan satu per satu namun tidakSeluruh pihak yang tidak dapat kami sebutkan satu per satu namun tidak mengurangi rasa hormat kami
mengurangi rasa hormat kami
Kami menyadari bahwa makalah ini masih jauh dari kesempurnaan. Maka dari itu Kami menyadari bahwa makalah ini masih jauh dari kesempurnaan. Maka dari itu kritik dan saran yang membangun sangat kami harapkan demi penyempurnaan makalah kritik dan saran yang membangun sangat kami harapkan demi penyempurnaan makalah selanjutnya agar lebih baik.
selanjutnya agar lebih baik.
Semoga makalah ini dapat bermanfaat bagi yang membacanya. Semoga makalah ini dapat bermanfaat bagi yang membacanya.
Bandung,
Bandung, 29 Septe29 September mber 20162016
Penyusun Penyusun
BAB I BAB I
PENDAHULUAN PENDAHULUAN
A.
A. Latar Belakang MasalahLatar Belakang Masalah
Ilmu matematika sering disebut sebagai sentral ilmu pengetahuan atau Ilmu matematika sering disebut sebagai sentral ilmu pengetahuan atau pusatnya
pusatnya ilmu ilmu pengetahuan pengetahuan karena karena matemamatematika tika digunakan, digunakan, diterapkan, diterapkan, dandan dibutuhkan untuk mendukung ilmu pengetahuan yang lain.
dibutuhkan untuk mendukung ilmu pengetahuan yang lain. Sebab banyak bidang-Sebab banyak bidang- bidang ilmu yang lain te
bidang ilmu yang lain terikat dengan ilmrikat dengan ilmu matematika, su matematika, seperti bidang keeperti bidang kedokteran,dokteran, biologi,
biologi, fisika, fisika, lingkungan, lingkungan, forensik, forensik, astronomi, fastronomi, farmasi, ilmu armasi, ilmu bahan, bahan, komputer,komputer, dan sebagainya. Berbagai bidang di atas juga tidak lepas dari peran matematika. dan sebagainya. Berbagai bidang di atas juga tidak lepas dari peran matematika. Sehingga da
Sehingga dapat diartikan pat diartikan bahwa bahwa matemmatematika merupaatika merupakan dasar kan dasar dari dari ilmu dunia.ilmu dunia. Belakangan ini, ilmu matematika telah berkembang pesat. Bukan hanya Belakangan ini, ilmu matematika telah berkembang pesat. Bukan hanya sebatas hitung menghitung menggunakan skala statistik, nilai, angka-angka real, sebatas hitung menghitung menggunakan skala statistik, nilai, angka-angka real, kalkulus dan peluang. Akan tetapi, perkembangan ilmu matematika juga terjadi kalkulus dan peluang. Akan tetapi, perkembangan ilmu matematika juga terjadi didasarkan pada penalaran
didasarkan pada penalaran – – penalaran yang logis atas sistem matematis. Penalaran penalaran yang logis atas sistem matematis. Penalaran yang dilakukan oleh para ahli matematik diperoleh atas realita kehidupan yang yang dilakukan oleh para ahli matematik diperoleh atas realita kehidupan yang nyata yang dirasakan oleh manusia. Perkembangan dan aplikasi dan bagian nyata yang dirasakan oleh manusia. Perkembangan dan aplikasi dan bagian matematik ini sangat dirasakan oleh manusia di berbagai kehidupan. Penalaran matematik ini sangat dirasakan oleh manusia di berbagai kehidupan. Penalaran inilah dalam bahasa matematika sering disebut logika.
inilah dalam bahasa matematika sering disebut logika.
Dari latar belakang masalah di atas maka penulis akan menyusun salah Dari latar belakang masalah di atas maka penulis akan menyusun salah satu
satu pembahasan pembahasan matematika matematika yaitu yaitu tentang persamaan tentang persamaan logaritlogaritma, ma, pertidaksamaanpertidaksamaan logaritma, aplikasi logaritma dalam
logaritma, aplikasi logaritma dalam kehidupan sehari-hari beserta contohkehidupan sehari-hari beserta contoh – – contoh contoh soal dan
soal dan jawabannyajawabannya....
B.
B. Rumusan MasalahRumusan Masalah 1.
1. Bagaimana sejarah logaritma?Bagaimana sejarah logaritma? 2.
2. Apa pengertian dan fungsi Apa pengertian dan fungsi logaritma?logaritma? 3.
3. Apa saja sifat- sifat fungsi logaritma?Apa saja sifat- sifat fungsi logaritma? 4.
4. Bagaimana bentuk persamaan logaritma?Bagaimana bentuk persamaan logaritma? 5.
5. Bagaimana bentuk pertidaksamaan logaritma?Bagaimana bentuk pertidaksamaan logaritma? 6.
C.
C. Tujuan MasalahTujuan Masalah 1.
1. Dapat mengetahui sejarah logaritmaDapat mengetahui sejarah logaritma 2.
2. Dapat mengetahui pengertian dan fungsi logaritmaDapat mengetahui pengertian dan fungsi logaritma 3.
3. Dapat mengetahui sifat-saifat fungsi Dapat mengetahui sifat-saifat fungsi logaritmalogaritma 4.
4. Dapat mengetahui persamaan logaritmaDapat mengetahui persamaan logaritma 5.
5. Dapat mengetahui Dapat mengetahui pertidaksampertidaksamaan laan logaritmaogaritma 6.
BAB II BAB II
PEMBAHASAN PEMBAHASAN A.
A. Sejarah LogaritmaSejarah Logaritma
Logaritma ditemukan oleh John Napier yang lahir pada tahun 1550 di dekat Logaritma ditemukan oleh John Napier yang lahir pada tahun 1550 di dekat Edinburgh, Skotlandia.Dia juga mendesain sebuah metode
Edinburgh, Skotlandia.Dia juga mendesain sebuah metode sederhana untuk perkalian dansederhana untuk perkalian dan pembagia
pembagian n yang yang dikenal dikenal sebagai sebagai tulang-tulang tulang-tulang Napier.Ketika Napier.Ketika buku buku Napier Napier tentangtentang logaritma diterbitkan pada tahun 1614, hal ini amat mengagumkan para ilmuwan logaritma diterbitkan pada tahun 1614, hal ini amat mengagumkan para ilmuwan sebagaimana ditemukannya kalkulator di zaman modern. Dengan bantuan logaritma sebagaimana ditemukannya kalkulator di zaman modern. Dengan bantuan logaritma mereka dapat mengerjakan perkalian dan pembagian yang sulit dengan cara cepat dan mereka dapat mengerjakan perkalian dan pembagian yang sulit dengan cara cepat dan mudah untuk pertama kalinya. Napier menghabiskan hidupnya mengutak-atik mudah untuk pertama kalinya. Napier menghabiskan hidupnya mengutak-atik matematika.Ia meninggal pada tahun 1617 pada usia 67 tahun da dimakamkan di matematika.Ia meninggal pada tahun 1617 pada usia 67 tahun da dimakamkan di Edinburgh.
Edinburgh.
Logaritma sendiri merupakan salah satu rumusan dalam matematika yang Logaritma sendiri merupakan salah satu rumusan dalam matematika yang digunakan untuk menyederhanakan perhitungan. Selain untuk penyederhanaan digunakan untuk menyederhanakan perhitungan. Selain untuk penyederhanaan perhitungan, logaritma juga
perhitungan, logaritma juga digunakan dalam berbagai digunakan dalam berbagai disiplin ildisiplin ilmu, seperti mu, seperti menghitungmenghitung bunga bank, la
bunga bank, laju pertumbuhan baju pertumbuhan bakteri,dan umkteri,dan umur fosil.ur fosil.
B.
B. Pengertian Fungsi LogaritmaPengertian Fungsi Logaritma
Fungsi logaritma adalah fungsi yang peubah bebasnya berupa bentuk logaritma. Fungsi logaritma adalah fungsi yang peubah bebasnya berupa bentuk logaritma. Fungsi logaritm
Fungsi logaritma merupakaa merupakan n invers dari einvers dari eksponen. Fungksponen. Fungsi logaritmasi logaritma f f dengan bilangandengan bilangan pokok atau
pokok atau basisbasisaadapat dituliskan dalam bentukdapat dituliskan dalam bentuk
Dengan Dengan 1.
1. x adalah x adalah peubah bebas, peubah bebas, atau numerous atau numerous dan berlaku sebagai dan berlaku sebagai daerah asal daerah asal (domain) (domain) fungsifungsi f
f yaitu Dyaitu Df f = { = { x x || x x > 0,> 0, x x
∈∈
R R}}2.
2. aa adalah bilangan pokok adalah bilangan pokok atau basis logaritma dengan ketentuanatau basis logaritma dengan ketentuan aa > 0 dan> 0 dan aa≠ 1≠ 1
:
C.
C. Grafik Fungsi LogaritmaGrafik Fungsi Logaritma
Ditinjau dari bilangan pokoknya grafik fungsi logaritma y = f(x) =
Ditinjau dari bilangan pokoknya grafik fungsi logaritma y = f(x) = aalog x dapatlog x dapat
dikelompokan menjadi 2 macam yaitu : grafik fungsi logaritma dengan bilangan pokok dikelompokan menjadi 2 macam yaitu : grafik fungsi logaritma dengan bilangan pokok
> 1
> 1
dan grafik fungsi logaritma dengan bilangan pokok 0 <dan grafik fungsi logaritma dengan bilangan pokok 0 < < 1
< 1
Untuk menggambaUntuk menggambar grafik atau r grafik atau kurva fungsi logaritma y = f(x) kurva fungsi logaritma y = f(x) ==aalog x ditempuh prosedurlog x ditempuh prosedur
sebagai berikut: sebagai berikut: a.
a. Buatlah tabel yang menunjukan relasi antara x dengan y =Buatlah tabel yang menunjukan relasi antara x dengan y =aalog xlog x
b.
b. GambarkGambarkan setiap an setiap titik (x,y) titik (x,y) yang diperoleh pada bidang kartesiusyang diperoleh pada bidang kartesius c.
c. Hubungkan setiap titik (x,y) yang diperoleh dari langkah b Hubungkan setiap titik (x,y) yang diperoleh dari langkah b dengan kurva.dengan kurva. Sehingga diperoleh grafik atau kurfa fungsi logaritma y = f(x)
Sehingga diperoleh grafik atau kurfa fungsi logaritma y = f(x) ==aalog xlog x
Ada dua cara dalam menggambarkan grafik fungsi logaritma yaitu dengan menggunakan Ada dua cara dalam menggambarkan grafik fungsi logaritma yaitu dengan menggunakan grafik fungsi eksponen dan substitusi titik.
grafik fungsi eksponen dan substitusi titik. a.
a. MenggunakMenggunakan Grafik an Grafik Fungsi EksponenFungsi Eksponen Grafik fungsi
Grafik fungsi y y = = aa log log x x dapat diperoleh dari grafik fungsi inversnya yaitu dapat diperoleh dari grafik fungsi inversnya yaitu y y = = aa x x. Untuk. Untuk melukis grafik
melukis grafik y y = =aa log log x x, kurva, kurva y y = = aa x x dapat dicerminkan terhadap garis dapat dicerminkan terhadap garis y y = = x x seperti contoh seperti contoh di bawah ini.
di bawah ini.
Contoh: Contoh:
Gambark
Gambarkan grafik an grafik fungsifungsi y y = =22 log log x x dengan menggunakan grafik dengan menggunakan grafik y y = 2 = 2 x x
berikut. berikut.
Bila
Bila y y = 2= 2 x x dicerminkan terhadap garis dicerminkan terhadap garis y y == x x, seperti tampak pada gambar di atas, maka, seperti tampak pada gambar di atas, maka hasil pencerminan dari
hasil pencerminan dari y y = 2 = 2 x x adalah adalah y y = = 22 log log x x..
Apabila disatukan maka bentuk gafiknya adalah sebagai berikut : Apabila disatukan maka bentuk gafiknya adalah sebagai berikut :
b.
b. Substitusi TitikSubstitusi Titik
Misalkan kita akan menggambar grafik dari
Untuk membantu kita dalam melukis grafik fungsi logaritma, mula-mula pili
Untuk membantu kita dalam melukis grafik fungsi logaritma, mula-mula pili h nilaih nilai y y yang yang terletak pada selang yang diketahui, kemudian substitusikan ke
terletak pada selang yang diketahui, kemudian substitusikan ke f f (( x x) untuk memperoleh) untuk memperoleh nilai nilai x x..
y=y= 33 log log x x x x -3 -3 -2 -2 -1 -1 0 0 1 1 2 2 33 y y11
27
27
11
99
11
33
1 1 3 3 9 9 2727Titik yang diperoleh dilukiskan pada diagram kartesius berupa titik (bulatan kecil). Titik Titik yang diperoleh dilukiskan pada diagram kartesius berupa titik (bulatan kecil). Titik tersebut dihubungkan sehingga membentuk kurva
tersebut dihubungkan sehingga membentuk kurva f f ( ( x x) =) = 33 log log x x seperti gambar di bawah seperti gambar di bawah
ini. ini.
Dari gambar di atas diperoleh bahwa: Dari gambar di atas diperoleh bahwa:
Bila nilaiBila nilai x x bertambah, maka nilai bertambah, maka nilai f f ( ( x x) bertambah, dan bila) bertambah, dan bila x x berkurang berkurangmendeka
mendekati nolti nol, maka nilai, maka nilai f f ( ( x x) juga ) juga semakin berkurangsemakin berkurang..
GarisGaris x x = 0 merupakan asimtot tegak. = 0 merupakan asimtot tegak.
Grafik fungsi logaritmaGrafik fungsi logaritma y y = =33 log log x x selalu naik untuk selalu naik untuk setiapsetiap x x, dengan kata lain, dengan kata lainfungsi
fungsi y y = =aa log log x xdengandengan aa > 1 > 1 merupakan fungsi naik.merupakan fungsi naik. Dengan demikian, dapat disimpulkan:
Dengan demikian, dapat disimpulkan:
Fungsi logaritma
Fungsi logaritma
y
y
= =aa log logx
x
dengan dengana
a
> 1 > 1 merupakan fungsi monoton naik, sebabmerupakan fungsi monoton naik, sebab bilaMisalkan kita akan menggambar dari grafik
Misalkan kita akan menggambar dari grafik y y = 13log = 13log x x untuk - untuk -3 ≤3 ≤ y y≤ 3,≤ 3, y yϵϵ Ɍ Ɍ.. Untuk membantu kita dalam melukis grafik fungsi logaritma, mula-mula pilih nilai Untuk membantu kita dalam melukis grafik fungsi logaritma, mula-mula pilih nilai y y yang terletak pada selang yang
yang terletak pada selang yang diketahui, kemudian substitusikan kediketahui, kemudian substitusikan ke f f ( ( x x).). y
y = = 1/31/3loglog x x
x
x -3 -3 -2 -2 -1 -1 0 0 1 1 2 2 33
y
y 27 27 9 9 3 3 1 1 3 3 9 9 2727
Titik yang diperoleh dilukiskan pada diagram kartesius berupa titik (bulatan kecil). Titik Titik yang diperoleh dilukiskan pada diagram kartesius berupa titik (bulatan kecil). Titik tersebut dihubungkan sehingga membentuk kurva
tersebut dihubungkan sehingga membentuk kurva y y = 13 log = 13 log x x seperti gambar di bawah in seperti gambar di bawah in
Dari gambar di atas diperoleh bahwa: Dari gambar di atas diperoleh bahwa:
Bila nilaiBila nilai x x bertambah, maka nilai bertambah, maka nilai f f ( ( x x) berkurang dan bila) berkurang dan bila x x berkurang mendekati berkurang mendekati nol, maka nilainol, maka nilai f f ( ( x x) semakin besar.) semakin besar.
GarisGaris x x = 0 merupakan asimtot tegak. = 0 merupakan asimtot tegak.
Grafik fungsi logaritmaGrafik fungsi logaritma y y = 13log = 13log x x selalu turun untuk setiap selalu turun untuk setiap x x, dengan kata lain, dengan kata lainfungsi
fungsi y y = =aa log log x x dengan 0 < dengan 0 < aa < 1 < 1 merupakamerupakan fungsi turun.n fungsi turun. Dengan demikian, dapat disimpulkan:
Dengan demikian, dapat disimpulkan:
Fungsi logaritma
Fungsi logaritma
y
y
= =aa log logx
x
dengan 0 < dengan 0 <a
a
< < 1 merupakan fungsi monoton turun, sebab1 merupakan fungsi monoton turun, sebab bilaJika grafik
Jika grafik y y = = 33 log log x x dan dan y y = 13log = 13log x x digambar pada satu diagram maka grafiknya adalah digambar pada satu diagram maka grafiknya adalah
sebagai berikut. sebagai berikut.
Berdasarkan gambar di atas, dapat diperoleh bahwa: Berdasarkan gambar di atas, dapat diperoleh bahwa:
GrafikGrafik y y = =aalog
log x x dengan 0 < dengan 0 < aa < 1 dapat diperoleh dengan mencerminkan grafik < 1 dapat diperoleh dengan mencerminkan grafik y y =
=aa log log x xdengandengan aa >1 terhadap sumbu >1 terhadap sumbu x x..
GrafikGrafik y y = =aa log log x x dengan 0 < dengan 0 < aa < 1 dan < 1 dan y y = =aa log log x x dengan dengan aa >1 berpotongan di titik >1 berpotongan di titik (1, 0)(1, 0)
JikaJika x x11 dan dan x x22 adalah dua buah titik adalah dua buah titik sembarang pada grafik dansembarang pada grafik dan x x22 > > x x11, maka, maka aalog log x
x22 > >aa log log x x11 untuk untuk aa > 1 dan > 1 dan aa log log x x22 < <aa log log x x11 untuk 0 < untuk 0 < aa < 1. < 1.
y y = = f f ( ( x x)) aalog
log x x merupakan fungsi naik untuk merupakan fungsi naik untuk aa > 1 dan merupakan fungsi turun > 1 dan merupakan fungsi turun untuk 0 <
untuk 0 < aa < 1. < 1.
Mari kita mencermati beberapa contoh soal berikut i Mari kita mencermati beberapa contoh soal berikut i ni.ni.
Contoh 1
Contoh 1 Gambarlah grafik dariGambarlah grafik dari y y = =22 log ( log ( x x – – 1). 1).
Penyelesaian:
Penyelesaian:
Untuk mempermuda
Untuk mempermudah perhitungan, mula-mula pih perhitungan, mula-mula pilih nilailih nilai y y yang terletak di sumbu yang terletak di sumbu y y positif, positif, y
Nilai
Nilai y y tersebut kemudian disubstitusikan ke tersebut kemudian disubstitusikan ke f f ( ( x x).). Hasil dari substitusi titik dapat
Hasil dari substitusi titik dapat dituliskan pada tabel berikut.dituliskan pada tabel berikut.
Titik yang terdapat pada tabel dilukiskan pada diagram kartesius berupa titik (bulatan Titik yang terdapat pada tabel dilukiskan pada diagram kartesius berupa titik (bulatan kecil). Titik tersebut dihubungkan sehingga membentuk kurva
kecil). Titik tersebut dihubungkan sehingga membentuk kurva y y == 22 log ( log ( x x – – 1) seperti 1) seperti
gambar di bawah ini. gambar di bawah ini.
Pada gambar di atas terlihat garis
Pada gambar di atas terlihat garis x x = 1 merupakan asimtot tegak. = 1 merupakan asimtot tegak.
Contoh 2
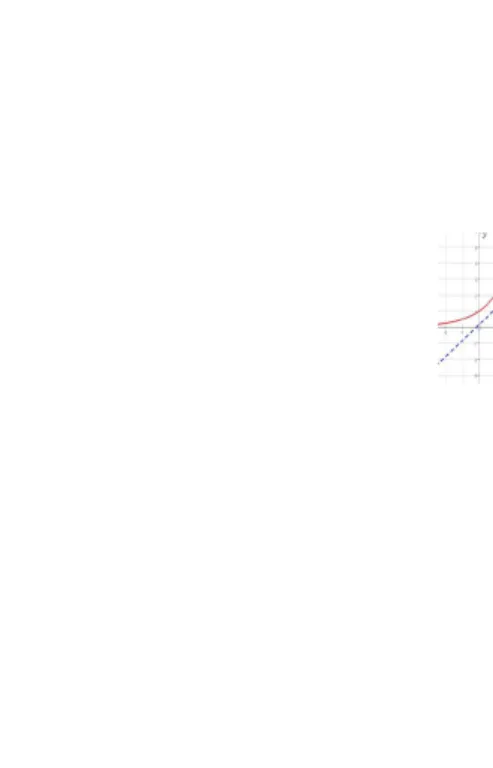
Contoh 2 Gambarlah grafik fungsiGambarlah grafik fungsi f f ( ( x x) = 13log) = 13log x x dan dan g g ( ( x x) = (13)) = (13) x x . .
Penyelesaian:
Penyelesaian:
Oleh karena
Oleh karena f f ( ( x x) = 13log) = 13log x x adalah invers dari adalah invers dari g g ( ( x x) = (13)) = (13) x x , maka dari grafik g , maka dari grafik g ( ( x x) dapat) dapat diperoleh dari
diperoleh dari f f ( ( x x) dengan mencerminkan) dengan mencerminkan g g ( ( x x) terhadap garis) terhadap garis y y = = x x.. Mula-mula gambarkan grafik
Untuk memperm
Untuk mempermudah perhitungan, pilih udah perhitungan, pilih nilainilai y y yang terletak di sumbu yang terletak di sumbu y y positif, positif, y y = 0 dan = 0 dan sumbu
sumbu y y negatif. negatif. Nilai
Nilai y y tersebut kemudian disubstitusikan ke tersebut kemudian disubstitusikan ke f f ( ( x x) untuk memperoleh nilai) untuk memperoleh nilai x x..
Dengan cara perhitungan yang sama dengan contoh-contoh sebelumnya diperoleh nilai ( Dengan cara perhitungan yang sama dengan contoh-contoh sebelumnya diperoleh nilai ( x x,, y
y) seperti pada tabel berikut.) seperti pada tabel berikut.
Nilai
Nilai (( x x,, y y) yang ada pada tabel dilukiskan pada diagram kartesius berupa titik (bulatan) yang ada pada tabel dilukiskan pada diagram kartesius berupa titik (bulatan kecil) kemudian dihubungkan sehingga membentuk kurva
kecil) kemudian dihubungkan sehingga membentuk kurva f f ( ( x x) = 13log) = 13log x x.. Kurva
Kurva f f ( ( x x) = 13log) = 13log x x kemudian dicerminkan terhadap garis kemudian dicerminkan terhadap garis y y = = x x, sehingga diperoleh kurva, sehingga diperoleh kurva g
g ( ( x x) = (13)) = (13) x x seperti grafik di bawah ini. seperti grafik di bawah ini.
Contoh :
Contoh :Tentukan domain dari fungsiTentukan domain dari fungsi f f ( ( x x) = log (3) = log (3 – – 4 x 4 x).).
Penyelesaian:
Penyelesaian:
Untuk menentukan domain (daerah asal) dari fungsi
Untuk menentukan domain (daerah asal) dari fungsi f f ( ( x x) = log (3) = log (3 – – 4 4 x x), kita memerlukan), kita memerlukan syarat numerus logaritma, yaitu:
syarat numerus logaritma, yaitu:
33 44 >
> 00
↔ 4 > 3
↔ 4 > 3
↔
↔ >>
Jadi, domain (Jadi, domain ( D D f f ) dari fungsi) dari fungsi f f ( ( x x) = log (3) = log (3 – – 4 4 x x) adalah:) adalah:
{ ⃓ <
{ ⃓ <
, , ∈
∈
Contoh : Contoh :
Gambarlah sketsa graf
Gambarlah sketsa grafik fungsi dari ik fungsi dari fungsi logaritma berikut :fungsi logaritma berikut :
==
1/21/2
xxJawab : Jawab :
=
=
dan dan ==
1/21/2
x untuk nilai-nilai terterntu :x untuk nilai-nilai terterntu :
=
=
==
1/21/2
xx x 8 4 2 1 x 8 4 2 111
22
11
44
11
88
y -3 y -3 -2 -2 -1 -1 0 0 1 1 2 2 33Adapun grafiknya adalah sebagai berikut : Adapun grafiknya adalah sebagai berikut :
x -3
x -3 -2 -2 -1 -1 0 0 1 1 2 2 33
y 8 4 2 1
y 8 4 2 1
11
perhatikan gra
perhatikan grafikfik
==
1/21/2
x, sifat-sifatnya adalah sebagai berikut :x, sifat-sifatnya adalah sebagai berikut :1.
1. Selalu disebelah kanan sumbu y, yang berarti terdefinisi hanya untuk x>0Selalu disebelah kanan sumbu y, yang berarti terdefinisi hanya untuk x>0 2.
2. Memotong sumMemotong sumbu x hanya di titik bu x hanya di titik (1,0)(1,0) 3.
3. Monoton turun, yang berarti jika xMonoton turun, yang berarti jika x11>x>x22>0 maka>0 maka1/21/2
x <x <1/21/2log xlog x004.
4. MempunyMempunyai asimtot tegak yaitu ai asimtot tegak yaitu x = 0 x = 0 atau sumbu y.atau sumbu y.
D.
D. SifatSifat – – Sifat Fungsi Logaritma Sifat Fungsi Logaritma
Sifat
Sifat – – sifat fung sifat fungsi logaritma si logaritma y y = f(x) == f(x) =aalog x dengan bilangan pokoklog x dengan bilangan pokok
> 1
> 1
0 <
0 <
< 1
< 1
sebagai berikut sebagai berikut1.
1. Domain fungsiDomain fungsi
adalah adalah
== { {| > 0 ∈
| > 0 ∈ }}
atau atau
= = 0,0,∞∞
2.
2. Range fungsiRange fungsi
adalah adalah
= ={{| ∈
| ∈ }}
atau atau
= R = R3.
3. RangeRange
kontinu pada kontinu pada0,0,∞∞
4.
4. FungsiFungsi
monoton naik untuk monoton naik untuk > 1
> 1
5.
5. FungsiFungsi
monoton turun untuk 0 < monoton turun untuk 0 < < 1
< 1
6.
6. JikaJika
> 1
> 1
maka nilaimaka nilai aalog x positif untuklog x positif untuk > 1
> 1
dan negatif untuk 0 < dan negatif untuk 0 < < 1
< 1
7.7. Jika 0 <Jika 0 <
< 1
< 1
maka nilai maka nilai aalog x log x positif untuk positif untuk 0 <0 < < 1 > 1
< 1 > 1
8.9.
9. Fungsi logaritma selalu memotong sumFungsi logaritma selalu memotong sumbu x dititibu x dititik (1,0) dengan kata laink (1,0) dengan kata lainaa
log x
log x
= 0 ↔ = 1
= 0 ↔ = 1
10.
10. aalog log x = 1 jika x = 1 jika dan hanya dan hanya jikajika
=
=
11.11. sumbu y asimtot tegaksumbu y asimtot tegak
12.
12. f ungsif ungsi
merupakan fungsi bijektif merupakan fungsi bijektif atau korespondensi satu-satuatau korespondensi satu-satu13.
13. grafik fungsi logaritma y =grafik fungsi logaritma y = aa
log x
log x
untukuntuk > 1
> 1
dengan fungsi logaritma y = dengan fungsi logaritma y = aaloglogx dan untuk 0 <
x dan untuk 0 <
< 1
< 1
dengan fungsi dengan fungsi logaritmanylogaritmanyaalog
log
adalah setangkup adalah setangkupsimetris terhadap sumbu x. simetris terhadap sumbu x. Contoh soal :
Contoh soal : 1.
1. Carilah invers fungsi eksponen f : (Carilah invers fungsi eksponen f : (
∞
∞,,∞ →
∞ →
dengandengan : 3
: 3
11
Jawab :Jawab :
=
= =
= 33
11
Pindahkan
Pindahkan
,
,
maka diperolehmaka diperoleh = 3
= 3
11
33
= = 1
= = 1
3
3loglog
3 3
= =
33loglog
11
2y =
2y =33loglog
11
y =
y =
33loglog
11
JadiJadi
−
−
= =
33loglog
11
y
y adalah peubah tak bebas, adalah peubah tak bebas, dan berlaku sebagai daerah hasil ( dan berlaku sebagai daerah hasil ( range ) fungsi, yaitu range ) fungsi, yaitu R R f f = { = {
y
y || y y
∈∈
R R}.}.E.
E. Persamaan LogaritmaPersamaan Logaritma
Persamaan logaritma adalah persamaan yang variabelnya sebagai numerus atau sebagai Persamaan logaritma adalah persamaan yang variabelnya sebagai numerus atau sebagai bilangan pokok
bilangan pokok dari suatu logaritmdari suatu logaritma. Perhatikan a. Perhatikan contoh berikut ini :contoh berikut ini :
log
log
++log
log2
2 11
= = 1 1 merupakan persamaan merupakan persamaan logaritlogaritma ma yang yang numerusnyanumerusnyamemuat variabel x. memuat variabel x.
55log4
log4
+ +55log
log
22 = = 0 0 merupakan persamaan merupakan persamaan logarilogaritma yang tma yang numerusnya memuatnumerusnya memuatvariabel y. variabel y.
Ada
Ada beberapa bentuk pebeberapa bentuk persamaan logrsamaan logaritma ini, diantaranya :aritma ini, diantaranya :
a)
a) aa
= =aa
jika
jikaaa
log
log
= =aalog
log
,,
> > 0, m0, makaaka
= = mm..Contoh soal : Contoh soal :
Tentukan penyelesaian
Tentukan penyelesaian 22
log 2
log 2
= 4= 4Jawab : Jawab :
2
2
log 2
log 2
= 4= 4 22
log 2
log 2
==22log2
log2
44x
x
––
2 2 = 2= 244x
x = = 1818
jadi, penyelesa
jadi, penyelesaianian22
log 2
log 2
= 4 adalah x = 18= 4 adalah x = 18 b)b) aa
= =aa
jika
jikaaa
log
log
= =aalog
log
, a > 0,, a > 0, a ≠ 1a ≠ 1,,
> 0, dan > 0, dan
) > 0 maka ) > 0 maka
= =
). ).Contoh soal : Contoh soal :
Tentukan penyelesaian
Tentukan penyelesaian 77
log10x 2
log10x 2
= =77log16x8
log16x8
Jawab : Jawab :
7
7
log10x2
log10x2
= =77log16x8
log16x8
10x + 10x + 2 2 = 16x= 16x
8 8 10x 10x
16x 16x ==
8 8
2 2
6x 6x ==
10 10 x x ==
sekarang selidiki apakah
sekarang selidiki apakah
> 0, dan > 0, dan
) > 0 ) > 0 ((10
10
66 ) = 1
) = 100((10
10
66 )
) 22
== 100
100
66 22
== 100
100
66
12
12
66 ==
112
112
66
((10
10
66 ) = 1
) = 166((10
10
66 ) ) 88
Karena
Karena untuk untuk x x ==
,,
> 0, dan > 0, dan
) > 0, maka x = ) > 0, maka x =
merupakan merupakan penyelesaiapenyelesaian.n. Jadi, penyelesaian
Jadi, penyelesaian77
log10x2
log10x2
= =77lologg16
16x
x 88
adalah x = adalah x =
c)
c) f f (x)(x)
= = f(x f(x ))
jika
jika f(x) f(x)
log
log
= = f(x) f(x)logℎ
logℎ
,,
> 0, > 0,
) > 0, ) > 0,ℎ
ℎ
) > 0, dan ) > 0, dan
≠ 1≠ 1, maka, maka
) =) =
ℎ
ℎ
). ).Contoh soal : Contoh soal :
Tentukan himpunan
Tentukan himpunan penyelesaiapenyelesaiannx-3x-3
log 1
log 1
= =x-3x-3log
log4
4 10
10
......Jawab : Jawab :
x-3
x-3
log
log
11
== x-3x-3log
log44
10
10
x x + + 1 1 = = 4x 4x + + 1010 x x
4x 4x = = 1010
1 1 -3x -3x = = 99 x x = = -3-3sekarang selidiki apakah
sekarang selidiki apakah
> 0, > 0,
≠ 1,≠ 1,
) > 0 ) > 0 dan danℎ
ℎ
) > 0 ) > 0 f(-3) f(-3) = -3 = -3
3 = -6 < 0 3 = -6 < 0 g(x) g(x) = - = -3 + 1 3 + 1 = = -2 < 0-2 < 0 oleh karena untuk x = -3oleh karena untuk x = -3
< 0 maka x = -3 bukan penyelesaian. < 0 maka x = -3 bukan penyelesaian. Jadi, himpunan penyelesaian dariJadi, himpunan penyelesaian dari x-3x-3
log 1
log 1
= =x-3x-3log
log4
4 10
10
adalahadalahØØ
F.
F. Pertidaksamaan LogaritmaPertidaksamaan Logaritma
Pada pembahasan sebelumnya, kalian telah mengetahui sifat
Pada pembahasan sebelumnya, kalian telah mengetahui sifat – – sifat fungsi sifat fungsi logaritma, yaitu sebagai berikut :
untuk a > 1, fungsiuntuk a > 1, fungsi
==aalog
log
merupakan fungsi naik. Artinya merupakan fungsi naik. Artinya,,untuk setiap setiap x
untuk setiap setiap x11, x, x22
∈∈ ℝℝ
berlaku x berlaku x11< x< x22 jika dan jika dan hanya jikahanya jikaf(x
f(x11) < f(x) < f(x22).).
Untuk 0 < a < 1, fungsiUntuk 0 < a < 1, fungsi
== aalog
log
merupakan fungsi turun. merupakan fungsi turun.Artinya,
Artinya, untuk setiap setiap xuntuk setiap setiap x11, , xx22
∈∈ ℝℝ
berlaku x berlaku x11< < xx22 jika jika dandanhanya jika f(x
hanya jika f(x11) > f(x) > f(x22).).
Sifat
Sifat – – sifat sifat ini berguna untuk ini berguna untuk menyelesamenyelesaikan pertidaksamaikan pertidaksamaan logaritma.an logaritma. Contoh soal :
Contoh soal :
Tentukan himpunan penyelesaian
Tentukan himpunan penyelesaian 33
log 5
log 5
> 0> 0Jawab : Jawab :
3
3
log 5
log 5
> 0> 0 33
log 5
log 5
>>33log1
log1
x + 5 >
x + 5 > 1 1 ... karena a . karena a > 1, ma> 1, maka fungsi ka fungsi naiknaik x > -4
x > -4
perhatikan pula
perhatikan pula bahwa numebahwa numerusnya harus lerusnya harus lebih dari nol, berabih dari nol, berartirti x + 5 > 0. Di dapat x > -5
x + 5 > 0. Di dapat x > -5 jadi himpunan pe
jadi himpunan penyelesaiannyelesaian33
log 5
log 5
> 0 adalah HP = { x> 0 adalah HP = { x
x > -5 atau x > - x > 5 atau x >-4 , x
4 , x
∈∈ ℝℝ
} } 1.1. Tentukan himpunan penyelesaian persamaan logaritma berikutTentukan himpunan penyelesaian persamaan logaritma berikut
log
log
- -log3
log3
==log
log
33
log
log
==log
log
33
==
33
3( x 3( x – – 3) 3) = = xx 3x 3x – – 9 9 = = xx2x
2x = = 99 x
x ==
jadi himpunan pejadi himpunan penyelesaiannyelesaiannya adalahnya adalah x x = =
2.
2. 22
log
logx2
x2 – – 2x
2x 44
= =22logx 4
logx 4
x x22 – – 2x + 2x + 4 4 = = x x + + 44 x x22 – – 2x-x 2x-x + + 4-4 4-4 = = 00 x x22 – – 3x 3x = = 00 x(x x(x – – 3) = 0 3) = 0 x = 0 atau x = 3 x = 0 atau x = 3 Selidiki apakah
Selidiki apakah f(x) f(x)
0 dan 0 dan g(x) g(x)
0 0 f(0) f(0) = x= x22 – – 2x + 4 2x + 4 = = 0 022 – – 2.0 + 4 2.0 + 4 = = 4 4 (4(4
0 ) 0 ) g(0) g(0) = x + 4= x + 4 = 0 + 4 = 0 + 4 = 4 = 4 f(3) f(3) = x= x22 – – 2x + 4 2x + 4 = = 3 322 – – 2.3 + 4 2.3 + 4 = = 7 7 (7(7
0 ) 0 ) g(3) g(3) = x + 4= x + 4 = 3 + 4 = 3 + 4 = 7 = 7Jadi penyeleaiannya x = 0 dan x = 3 Jadi penyeleaiannya x = 0 dan x = 3 3.
3 34(x+2)4(x+2)= 3= 3x+2x+2 4(x+2) = x + 2 4(x+2) = x + 2 4x + 8 4x + 8 = x = x + 2+ 2 4x 4x – – x = 2 x = 2 – – 8 8 3x 3x = = -6-6 X X = = -2-2 Jadi
Jadi penyelesapenyelesaian ian 8181x+2x+2 = 3 = 3x+2x+2 adalah x = -2 adalah x = -2
4.
4. tentukanlah tentukanlah penyelesapenyelesaian dari 9 ian dari 9 = = 7297292-4x2-4x
9 911 = = 993(2-4x)3(2-4x) 3(2-4x) 3(2-4x) = = 11 6 6 – – 12x 12x = = 11 -12x -12x = = 11 – – 6 6 -12x -12x = = -5-5 x x ==
JadiJadi penyelesapenyelesaian ian 9 9 = = 7297292-4x2-4x adalah x =adalah x =
5. Tentukan penyelesaian dari 4
5. Tentukan penyelesaian dari 4x+5x+5 = 2= 2
2 22(x+5)2(x+5) = 2= 2 2(x 2(x + + 5) 5) = = 11 2x 2x + + 10 10 = = 11 2x 2x = = 11 – – 10 10 x x = = -9-9 Jadi
G.
G. APLIKASI DALAM KEHIDUPAN APLIKASI DALAM KEHIDUPAN SEHARI-HARISEHARI-HARI
Sebelum ada kalkulator elektronik, logaritma digunakan sepanjang waktu untuk Sebelum ada kalkulator elektronik, logaritma digunakan sepanjang waktu untuk melakukan perhitungan ekspone
melakukan perhitungan eksponensial. Jadi para ilnsial. Jadi para ilmuwan dan insinyur dari semuamuwan dan insinyur dari semua jenis memanfa
jenis memanfaatkan sering menggatkan sering menggunakan. Misalnya, jika Anda ingin munakan. Misalnya, jika Anda ingin menemukanenemukan 4 pangkat 3.5,
4 pangkat 3.5, Anda akan menggunakan fakta bahwa:Anda akan menggunakan fakta bahwa: 4 ^ (3.5) = 10 Log ^ [4 ^ 3.5] = 10 ^ (3.5 * log (4)) 4 ^ (3.5) = 10 Log ^ [4 ^ 3.5] = 10 ^ (3.5 * log (4))
Anda melihat log (4)
Anda melihat log (4) dalam tabel log Anda, kalikan dengan 3,5, dalam tabel log Anda, kalikan dengan 3,5, kemudiankemudian gunakan tabel log untuk menemukan antilog pada (10 pangkat jawaban Anda). gunakan tabel log untuk menemukan antilog pada (10 pangkat jawaban Anda). Hari ini, kita biasanya membiarkan kalkulator melakukan pekerjaan itu, tapi Hari ini, kita biasanya membiarkan kalkulator melakukan pekerjaan itu, tapi bahkan
bahkan kalkulator kalkulator menggunamenggunakan kan fakta-fakta fakta-fakta seperti seperti ini ini untuk untuk melakukamelakukann komputasi.
komputasi.
Saya telah membaca bahwa penggunaan logaritma membuat begitu Saya telah membaca bahwa penggunaan logaritma membuat begitu banyak h
banyak hal mungkal mungkin bahwa in bahwa itu adalah itu adalah salah salah satu kontrsatu kontribusi utamibusi utama dari a dari matemamatematikatika ke dunia ilmu pengetahuan. Misalnya, sebelum ada logaritma, para astronom ke dunia ilmu pengetahuan. Misalnya, sebelum ada logaritma, para astronom merasa kesulitan dengan penjumlahan ataupun perkalian yang begitu merasa kesulitan dengan penjumlahan ataupun perkalian yang begitu besar.
besar. Dengan Dengan munculnya munculnya penggunaan penggunaan logaritma, logaritma, perkalian perkalian ataupun ataupun perpangkaperpangkatantan yang besar menjadi hal yang sederhana. Dalam kehidupan nyata, logaritma sangat yang besar menjadi hal yang sederhana. Dalam kehidupan nyata, logaritma sangat diperlukan bagi ilmu pengetahuan. Dalam sejarah ilmu pengetahuan, diperlukan bagi ilmu pengetahuan. Dalam sejarah ilmu pengetahuan, pengemba
pengembangan tabel logaritma dan penggunaannya merupngan tabel logaritma dan penggunaannya merupakan prestasi yang luarakan prestasi yang luar biasa.
biasa.
Para astronom masih menggunakan skala logaritmik untuk sumbu grafik Para astronom masih menggunakan skala logaritmik untuk sumbu grafik dan diagram. Penggunaan logaritma yang paling jelas adalah pada penghitungan dan diagram. Penggunaan logaritma yang paling jelas adalah pada penghitungan skala Richter untuk gempa bumi
skala Richter untuk gempa bumi dan desibel. Logaritma juga diaplikasikan dalamdan desibel. Logaritma juga diaplikasikan dalam penghitungan frek
penghitungan frekuensi musik.uensi musik.
Penggunaan lain fungsi logaritma adalah dalam bidang biologi, yaitu Penggunaan lain fungsi logaritma adalah dalam bidang biologi, yaitu untuk mengukur laju pertumbuhan penduduk, antropologi, dan keuangan (untuk untuk mengukur laju pertumbuhan penduduk, antropologi, dan keuangan (untuk menghitung bunga
H.
H. LATIHAN SOALLATIHAN SOAL
1.
1. Carilah invers fungsi eksponen f : (Carilah invers fungsi eksponen f : (
∞
∞,,∞ →
∞ →
dengandengan: 4
: 4
22log (3log (3 – – x) x)2.
2. Carilah himpunan penyelesaian dariCarilah himpunan penyelesaian dari88loglog
=
=
88log 12log 123.
3. Carilah himpunan penyelesaian dari logCarilah himpunan penyelesaian dari log
+
+
−
−
= -1 = -1 4.4. Carilah himpunan penyelesaian dari Carilah himpunan penyelesaian dari setiap persamaan logaritma berikutsetiap persamaan logaritma berikut22loglog
22 2233 = =
33loglog
22 2233
5.
5. Tentukan himpunan dari Tentukan himpunan dari pertidaksampertidaksamaan logaan log
44 44 ≤ lo
≤ logg 5
5 10
10
6.6. 55log 3x + 5 <log 3x + 5 < 55log 35log 35
7.
7. 33log (2x + 3) >log (2x + 3) >33log 15log 15
8.
8. 22log (6x + 2) <log (6x + 2) <22log (x + 27)log (x + 27)
9.
9. 22log (5xlog (5x – – 14) < 6 14) < 6
10.
10. 44log (2xlog (2x22 + 24) > + 24) >44log (xlog (x22 + 10x) + 10x)
11.
11. x+1x+1log (2xlog (2x – – 3) < 3) < x+1x+1log (x + 5)log (x + 5)
12.
12. 2x-52x-5log (xlog (x22 + 5x) > + 5x) >2x-52x-5log (4x + 12)log (4x + 12)
13.
13. 55log 3x + 5 <log 3x + 5 <55log 35log 35
14.
14. 33log (2x + 3) >log (2x + 3) >33log 15log 15
15.
15. 22log (6x + 2) <log (6x + 2) <22log (x + 27)log (x + 27)
16.
16. 22log (5xlog (5x – – 14) < 6 14) < 6
17.
17. 44log (2xlog (2x22 + 24) > + 24) >44log (xlog (x22 + 10x) + 10x) 18.
18. x+1x+1log (2xlog (2x – – 3) < 3) < x+1x+1log (x + 5)log (x + 5)
19.
19. 2x-52x-5log (xlog (x22 + 5x) > + 5x) >2x-52x-5log (4x + 12)log (4x + 12)
Jawaban: Jawaban: 1.
1. ((
∞
∞,,∞ →
∞ →
dengandengan: 4
: 4
22log (3log (3 – – x) + 1 x) + 1 y =g(x) = 4 y =g(x) = 4 22log (3log (3 – – x) + 1 x) + 1 tukarkan x dan y tukarkan x dan y x x = = 44 22log (3log (3 – – x) + 1 x) + 1 x x – – 1 = 4 1 = 4 22log (3log (3 – – x) + 1 x) + 1
11
= =22log (3log (3 – – y) y)y
y = = 3 3 --
22
11
jadijadi
−
−
=
= 33
22
11
2.
2. 88loglog
==
88log 12log 12
= 12 = 12
- 12 = 0- 12 = 0
44
−−3) =03) =0 = =
4 atau x = 34 atau x = 3 3. 3. loglog+
+
−
−
= -1 = -1 log log−
−
+
+
= =log
log
−
−
+
+
= =
10x -10 = 3x + 18 10x -10 = 3x + 18 7x = 28 7x = 28 x = 4 x = 4 4.4. 22loglog
22 2233 = =
33loglog
22 2233
22
223 =
3 =
11
22
224 =
4 = 00
(x + 4)(x (x + 4)(x – – 6) 6) Jadi hp nya adalah
Jadi hp nya adalah
{{4,6
4,6}}
5.
5. loglog
4
4
44 ≤ log 5
≤ log 5 10
10
log log
4
4
44 >
> 00
22
>
> 00
∈ ,
∈ , ≠
≠ 22
5
5 10 >
10 > 00
x x > > -2-2 loglog
44 44 ≤ log 5
≤ log 5 10
10
6 ≤ 0
6 ≤ 0
33
22 ≤
≤ 00
2 ≤ ≤ 3
2 ≤ ≤ 3
ℎ
ℎ {{|| 2 2 <
< ≤ 3
≤ 3}}
6.6. 55log 3x + 5 <log 3x + 5 <55log 35log 35
Syarat nilai bilangan pada logaritma 3x + 5 > 0 atau x > -5/3 ... Syarat nilai bilangan pada logaritma 3x + 5 > 0 atau x > -5/3 ... (1)(1) 3x + 5 < 35 3x + 5 < 35 3x < 30 3x < 30 x x < 1< 10 0 ....(2)....(2)
Jadi dari (1) dan (2) diperoleh penyelesaian -5/3 < x < 10. Jadi dari (1) dan (2) diperoleh penyelesaian -5/3 < x < 10.
7.
7. 33log (2x + 3) >log (2x + 3) >33log 15log 15
Syarat nilai bilangan pada logaritma 2x + 3 > 0 atau x > -3/2 ... Syarat nilai bilangan pada logaritma 2x + 3 > 0 atau x > -3/2 ... (1)(1) Perbandingan nilai pada l
Perbandingan nilai pada logaritmaogaritma 2x + 3 > 15 2x + 3 > 15 2x > 12 2x > 12 x > x > 6 6 ....(2)....(2) Jadi, dari (1)
Jadi, dari (1) dan (2) diperoleh penyelesaian x > 6.dan (2) diperoleh penyelesaian x > 6.
8.
8. 22log (6x + 2) <log (6x + 2) <22log (x + 27)log (x + 27)
Syarat nilai bilangan pada
Syarat nilai bilangan pada logaritma:logaritma: 6x + 2 > 0,
6x + 2 > 0, maka x > -1/3 .... (1)maka x > -1/3 .... (1) x + 27 > 0,
x + 27 > 0, maka x > -27 ... (2)maka x > -27 ... (2) Perbandingan nilai pada l
Perbandingan nilai pada logaritmaogaritma 6x + 2 < x + 27 6x + 2 < x + 27 6x 6x – – x < 27 x < 27 – – 2 2 5x < 25 5x < 25 x x < < 5 5 ... ... (3)(3)
Jadi, dari (1), (2),dan (3)
Jadi, dari (1), (2),dan (3) diperoleh penyelesadiperoleh penyelesaian -1/3 < ian -1/3 < x < 5x < 5
9.
9. 22log (5xlog (5x – – 16) < 6 16) < 6
Syarat nilai bilangan pada
5x
5x – – 16 > 0, maka x > 16/5 .... (1) 16 > 0, maka x > 16/5 .... (1) Perbandingan nilai pada l
Perbandingan nilai pada logaritmaogaritma
2
2log (5xlog (5x – – 16) < 16) <22log 26log 26 2
2log (5xlog (5x – – 16) < 16) <22log 64log 64
5x 5x – – 16 < 16 < 6464 5x < 80 5x < 80 x < 16 . . . . (2) x < 16 . . . . (2)
Jadi, dari (1) dan (2) diperoleh penyelesaian 16/5 < x < 16. Jadi, dari (1) dan (2) diperoleh penyelesaian 16/5 < x < 16.
10.
10. 44log (2xlog (2x22 + 24) > + 24) >44log (xlog (x22 + 10x) + 10x)
Syarat nilai pada
Syarat nilai pada logaritma.logaritma. 2x
2x22 + 24 > 0 (definit positif). Jadi, berla + 24 > 0 (definit positif). Jadi, berlaku untuk setiap x ku untuk setiap x . . . (1). . . (1)
x
x22 + 10x > 0, maka x < -10 + 10x > 0, maka x < -10 atau x > 0 . . . . (2)atau x > 0 . . . . (2)
Perbandingan nilai pada l
Perbandingan nilai pada logaritmaogaritma (2x (2x22 + + 24) 24) > > (x(x22 + 10x) + 10x) 2x 2x22 - x - x22 - 10x + 24 > 0 - 10x + 24 > 0 x x22 - 10x + 24 > 0 - 10x + 24 > 0 (x (x – – 4)(x 4)(x – – 6) > 6) > x < 4 atau x > 6 x < 4 atau x > 6 ....(3)....(3)
Jadi, dari (1), (2), dan (3) diperoleh penyelesaian x < -10 atau x > 6. Jadi, dari (1), (2), dan (3) diperoleh penyelesaian x < -10 atau x > 6.
11.
11. .. x+1x+1log (2xlog (2x – – 3) < 3) < x+1x+1log (x + 5)log (x + 5)
Syarat nilai pada bilangan x+1>0 Syarat nilai pada bilangan x+1>0
Batas ini dibagi menjadi 2,yaitu 0<x+1<1 dan x+1>1, sehingga diperoleh Batas ini dibagi menjadi 2,yaitu 0<x+1<1 dan x+1>1, sehingga diperoleh batas- batas berikut.
batas berikut. Untuk
Untuk 0<x+1<1 ata0<x+1<1 atau -1 < u -1 < x <0. . . x <0. . . (1)(1) Syarat nilai pada logaritma.
Syarat nilai pada logaritma. 2x
2x – – 3 3 > > 0, 0, maka maka x>3/2 x>3/2 . . . (2)(2) x
x + + 5 5 > > 0, 0, maka maka x x > > -5 -5 . . . (3)(3) Perbandingan nilai pada l
Perbandingan nilai pada logaritmaogaritma (2x (2x – – 3) 3) > > (x + (x + 5)5) 2x - x > 5 + 3 2x - x > 5 + 3 x x > > 8 8 ...(4)...(4)
Dari pe
Dari pertidaksamaartidaksamaan (1), n (1), (2), (3) (2), (3) dam dam (4), tidak (4), tidak ada irisanada irisan Penyelesaian:
Penyelesaian: Untuk
Untuk x+1>1 atau x+1>1 atau x > 0 . x > 0 . . . (1). . (1) Syarat nilai pada logaritma. Syarat nilai pada logaritma. 2x
2x – – 3 3 > > 0, 0, maka maka x>3/2 x>3/2 . . . (2)(2) x
x + + 5 5 > > 0, 0, maka maka x x > > -5 -5 . . . (3)(3) Perbandingan nilai pada
Perbandingan nilai pada logaritmalogaritma (2x (2x – – 3) 3) < < (x + (x + 5)5) 2x - x < 5 + 3 2x - x < 5 + 3 x x < < 8 8 ...(4)...(4) Dari pertidaksam
Dari pertidaksamaan (1), (2), (3) aan (1), (2), (3) dan (4), ada irisan penyelesaian yaitu 3/2 <xdan (4), ada irisan penyelesaian yaitu 3/2 <x < 8. Jadi,
< 8. Jadi, penyelesapenyelesaiannya adalah 3/2 <x< 8.iannya adalah 3/2 <x< 8.
.12.
.12.2x-52x-5log (xlog (x22 + 5x) > + 5x) >2x-52x-5log (4x + 12)log (4x + 12)
Syarat nilai pada bilangan 2x-5 > 0 Syarat nilai pada bilangan 2x-5 > 0 Batas ini dibagi
Batas ini dibagi menjadi 2,yaitu 0<2x-5<1 dan 2x-5>1, sehingga diperoleh menjadi 2,yaitu 0<2x-5<1 dan 2x-5>1, sehingga diperoleh batas-batasbatas-batas berikut.
berikut. Untuk
Untuk 0< 0< 2x-5 2x-5 <1 <1 atau atau 5/2 5/2 < < x x < < 3 3 . . . (1)(1) Syarat nilai pada logaritma.
Syarat nilai pada logaritma. x
x22+ 5x + 5x > > 0, 0, maka maka x x < < -5 -5 atau atau x x > > 0 0 . . . . . . (2)(2)
4x
4x + + 12 12 > > 0, 0, maka maka x x > > -3 -3 . . . (3)(3) Perbandingan nilai pada logaritma
Perbandingan nilai pada logaritma (x (x22 + 5x) < (4x + 5x) < (4x + 12)+ 12) x x22 + 5x - 4x - 12 < 0 + 5x - 4x - 12 < 0 x x22 + x - 12 < 0 + x - 12 < 0 (x + 4)(x - 3) < 0 (x + 4)(x - 3) < 0 -4 -4 < < x x < < 3 3 . . . (4)(4) Dari pertidaksam
Dari pertidaksamaan (1), (2), (3) aan (1), (2), (3) dan (4), ada irisan penyelesaian yaitu 5/2 < dan (4), ada irisan penyelesaian yaitu 5/2 < x < 3.x < 3. Untuk
Untuk 2x-5 2x-5 > > 1 1 atau atau x x > > 3 3 . . . (1)(1) Syarat nilai pada logaritma.
Syarat nilai pada logaritma. x
4x
4x - - 12 12 > > 0, 0, maka maka x x > > 3 3 . . . (3)(3) Perbandingan nilai pada logaritma
Perbandingan nilai pada logaritma (x (x22 + 5x) > (4x + 5x) > (4x + 12)+ 12) x x22 + 5x - 4x - 12 > 0 + 5x - 4x - 12 > 0 x x22 + x - 12 > 0 + x - 12 > 0 (x + 4)(x - 3) > 0 (x + 4)(x - 3) > 0 x x <-4 <-4 atau atau x x > > 3 3 . . . (4)(4) Dari pertidaksam
Dari pertidaksamaan (1), (2), (3) aan (1), (2), (3) dan (4), ada irisan penyelesaian yaitu x dan (4), ada irisan penyelesaian yaitu x > 3.> 3. Jika, kedua penyelesaian diga
Jika, kedua penyelesaian digabungkan maka diperoleh penyelesaiabungkan maka diperoleh penyelesaian x > n x > 5/2 dan x =/ 5/2 dan x =/ 3.3.
13.
13. 55log 3x + 5 <log 3x + 5 < 55log 35log 35
Syarat nilai bilangan pada logaritm
Syarat nilai bilangan pada logaritma 3x + 5 > a 3x + 5 > 0 atau x > -5/3 ... 0 atau x > -5/3 ... (1)(1) 3x + 5 < 35 3x + 5 < 35 3x < 30 3x < 30 x < x < 10 10 ....(2)....(2)
Jadi dari (1) dan (2) diperoleh penyelesaian -5/3 < x < 10. Jadi dari (1) dan (2) diperoleh penyelesaian -5/3 < x < 10.
14.
14. 33log (2x + 3) >log (2x + 3) > 33log 15log 15
Syarat nilai bilangan pada logaritm
Syarat nilai bilangan pada logaritma 2x + 3 > a 2x + 3 > 0 atau x > -3/2 ... 0 atau x > -3/2 ... (1)(1) Perbandingan nilai pada logaritma
Perbandingan nilai pada logaritma 2x + 3 > 15 2x + 3 > 15 2x > 12 2x > 12 x > x > 6 6 ....(2)....(2) Jadi, dari (1) dan
Jadi, dari (1) dan (2) diperoleh penyelesaian x > 6.(2) diperoleh penyelesaian x > 6.
15.
15. 22log (6x + 2) <log (6x + 2) <22log (x + 27)log (x + 27)
Syarat nilai bilangan pada logaritma: Syarat nilai bilangan pada logaritma: 6x + 2 > 0,
6x + 2 > 0, maka x > -1/3 .... (1)maka x > -1/3 .... (1) x + 27 > 0,
x + 27 > 0, maka x > -27 ... (2)maka x > -27 ... (2) Perbandingan nilai pada logaritma Perbandingan nilai pada logaritma 6x + 2 < x + 27
6x 6x – – x < 27 x < 27 – – 2 2 5x < 25 5x < 25 x x < < 5 5 ... ... (3)(3)
Jadi, dari (1), (2),dan (3)
Jadi, dari (1), (2),dan (3) diperoleh penyelesadiperoleh penyelesaian -1/3 < ian -1/3 < x < 5x < 5
16.
16. 22log (5xlog (5x – – 16) < 6 16) < 6
Syarat nilai bilangan pada logaritma: Syarat nilai bilangan pada logaritma: 5x
5x – – 16 > 0, maka x > 16/5 .... (1) 16 > 0, maka x > 16/5 .... (1) Perbandingan nilai pada logaritma Perbandingan nilai pada logaritma
2
2log (5xlog (5x – – 16) < 16) <22log 26log 26 2
2log (5xlog (5x – – 16) < 16) <22log 64log 64
5x 5x – – 16 < 16 < 6464 5x < 80 5x < 80 x < 16 . . . . (2) x < 16 . . . . (2)
Jadi, dari (1) dan (2) diperoleh penyelesaia
Jadi, dari (1) dan (2) diperoleh penyelesaian 16/5 < x < 16.n 16/5 < x < 16.
17.
17. 44log (2xlog (2x22 + 24) > + 24) >44log (xlog (x22 + 10x) + 10x)
Syarat nilai pada logaritma. Syarat nilai pada logaritma. 2x
2x22 + 24 > 0 (def + 24 > 0 (definit positif). Jadi, berinit positif). Jadi, berlaku untuk setiap x laku untuk setiap x . . . (1). . . (1)
x
x22 + 10x > + 10x > 0, maka x < 0, maka x < -10 -10 atau x > 0 . atau x > 0 . . . . (2). . . (2)
Perbandingan nilai pada logaritma Perbandingan nilai pada logaritma (2x (2x22 + + 24) > 24) > (x(x22 + 10x) + 10x) 2x 2x22 - x - x22 - 10x + 24 > 0 - 10x + 24 > 0 x x22 - 10x + 24 > 0 - 10x + 24 > 0 (x (x – – 4)(x 4)(x – – 6) > 6) > x < 4 atau x > x < 4 atau x > 6 ....(3)6 ....(3)
Jadi, dari (1), (2), dan (3) diperoleh penyelesaian x < -10 atau x > 6. Jadi, dari (1), (2), dan (3) diperoleh penyelesaian x < -10 atau x > 6.
18.
18. x+1x+1log (2xlog (2x – – 3) < 3) < x+1x+1log (x + 5)log (x + 5)
Syarat nilai pada bilangan x+1>0 Syarat nilai pada bilangan x+1>0 Batas ini dibagi
Batas ini dibagi menjadi 2,yaitu 0<x+1<1 dan x+1>1, sehingga diperoleh batas-batasmenjadi 2,yaitu 0<x+1<1 dan x+1>1, sehingga diperoleh batas-batas berikut.
Untuk
Untuk 0<x+1<1 atau 0<x+1<1 atau -1 < x -1 < x <0. . . (1)<0. . . (1) Syarat nilai pada logaritma.
Syarat nilai pada logaritma. 2x
2x – – 3 3 > > 0, 0, maka maka x>3/2 x>3/2 . . . (2)(2) x
x + + 5 5 > > 0, 0, maka maka x x > > -5 -5 . . . (3)(3) Perbandingan nilai pada logaritma Perbandingan nilai pada logaritma (2x (2x – – 3) 3) > > (x + (x + 5)5) 2x - x > 5 + 3 2x - x > 5 + 3 x x > > 8 8 ...(4)...(4) Dari pertidaksama
Dari pertidaksamaan (1), (2), (3) an (1), (2), (3) dam (4), tidak ada irisan penyelesaian.dam (4), tidak ada irisan penyelesaian.
Untuk
Untuk x+1>1 atau x+1>1 atau x > 0 . x > 0 . . . (1). . (1) Syarat nilai pada logaritma. Syarat nilai pada logaritma. 2x
2x – – 3 3 > > 0, 0, maka maka x>3/2 x>3/2 . . . (2)(2) x
x + + 5 5 > > 0, 0, maka maka x x > > -5 -5 . . . (3)(3) Perbandingan nilai pada logaritma Perbandingan nilai pada logaritma (2x (2x – – 3) 3) < < (x + (x + 5)5) 2x - x < 5 + 3 2x - x < 5 + 3 x x < < 8 8 ...(4)...(4) Dari pertidaksama
Dari pertidaksamaan (1), (2), (3) an (1), (2), (3) dan (4), ada irisan penyelesaian yaitu 3/2 <x < dan (4), ada irisan penyelesaian yaitu 3/2 <x < 8. Jadi,8. Jadi, penyelesaia
penyelesaiannya adalannya adalah 3/2 <x< 8.h 3/2 <x< 8.
19.
19. 2x-52x-5log (xlog (x22 + 5x) > + 5x) > 2x-52x-5log (4x + 12)log (4x + 12)
Syarat nilai pada bilangan 2x-5 > 0 Syarat nilai pada bilangan 2x-5 > 0 Batas ini dibagi
Batas ini dibagi menjadi 2,yaitu 0<2x-5<1 dan 2x-5>1, sehingga diperoleh menjadi 2,yaitu 0<2x-5<1 dan 2x-5>1, sehingga diperoleh batas-batasbatas-batas berikut.
berikut. Untuk
Untuk 0< 0< 2x-5 2x-5 <1 <1 atau atau 5/2 5/2 < < x x < < 3 3 . . . (1)(1) Syarat nilai pada logaritma.
Syarat nilai pada logaritma. x
x22+ 5x + 5x > > 0, 0, maka maka x x < < -5 -5 atau atau x x > > 0 0 . . . . . . (2)(2)
4x
4x + + 12 12 > > 0, 0, maka maka x x > > -3 -3 . . . (3)(3) Perbandingan nilai pada logaritma
(x (x22 + 5x) < (4x + 12) + 5x) < (4x + 12) x x22 + 5x - 4x - 12 < 0 + 5x - 4x - 12 < 0 x x22 + x - 12 < 0 + x - 12 < 0 (x + 4)(x - 3) < 0 (x + 4)(x - 3) < 0 -4 -4 < < x x < < 3 3 . . . (4)(4) Dari pertidaksam
Dari pertidaksamaan (1), (2), aan (1), (2), (3) dan (4), ada irisan (3) dan (4), ada irisan penyelesapenyelesaian yaitu 5/2 < ian yaitu 5/2 < x < 3.x < 3. Untuk
Untuk 2x-5 2x-5 > > 1 1 atau atau x x > > 3 3 . . . (1)(1) Syarat nilai pada logaritma.
Syarat nilai pada logaritma. x
x22+ 5x + 5x > > 0, 0, maka maka x x < < -5 -5 atau atau x x > > 0 0 . . . . . . (2)(2)
4x
4x - - 12 12 > > 0, 0, maka maka x x > > 3 3 . . . (3)(3) Perbandingan nilai pada logaritma
Perbandingan nilai pada logaritma (x (x22 + 5x) > (4x + 5x) > (4x + 12)+ 12) x x22 + 5x - 4x - 12 > 0 + 5x - 4x - 12 > 0 x x22 + x - 12 > 0 + x - 12 > 0 (x + 4)(x - 3) > 0 (x + 4)(x - 3) > 0 x x <-4 <-4 atau atau x x > > 3 3 . . . (4)(4) Dari pertidaksam
Dari pertidaksamaan (1), (2), (3) aan (1), (2), (3) dan (4), ada irisan dan (4), ada irisan penyelesapenyelesaian yaitu x ian yaitu x > 3. Jika, kedua> 3. Jika, kedua penyelesaia
Daftar Pustaka : Daftar Pustaka : H.F.S, Cecep Anwar. 2008.
H.F.S, Cecep Anwar. 2008. Matematika Ap Matematika Aplikasi.likasi. Jakarta: PT. Mutiara Bangsa Jakarta: PT. Mutiara Bangsa Noormandiri,
Noormandiri, B.K B.K dan dan Sucipto Sucipto Endar, Endar, 2004.2004. Matematika Matematika SMA SMA Untuk Untuk Kelas Kelas X X . Jakarta:. Jakarta: Erlangga
Erlangga Andi. 2003.