Aplikasi Turunan dalam Bidang Ekonomi - Spada UNS

1

Aplikasi Turunan dalam Bidang Ekonomi

Tugas dibuat untuk Memenuhi Proyek Akhir Makalah Mata Kuliah Kalkulus 1

Disusun Oleh :

1. Muhammad Baharuddin D. S. (K1317050) 2. Ayu May Lestari (K1318012) 3. Nafa’atul Ilmi Arriesty (K1318054) 4. Olivia Oktaviani (K1318064)

5. Venti Julianti (K1318078)

PROGRAM STUDI PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SEBELAS MARET 2021

2

DAFTAR ISI

Cover... 1

Daftar Isi ... 2

BAB I PENDAHULUAN... 3

A. Latar Belakang ... 3

B. Rumusan Masalah ... 4

C. Tujuan Penulis ... 4

BAB II PEMBAHASAN ... 5

A) Turunan ... 5

A. Konsep Turunan ... 5

B. Definisi Turunan ... 8

C. Aturan-Aturan Pencarian Turunan ... 9

D. Turunan Fungsi Trigonometri ... 10

E. Penerapan Turunan dalam Kehidupan Sehari-hari ... 10

B) Nilai Maksimum dan Minimum Suatu Fungsi ... 11

A. Nilai Maksimum dan Minimum Suatu Fungsi ... 11

B. Kemonotonan dan Kecekungan ... 14

C. Penerapan Nilai Maksimum dan Minimum dalam Kehidupan Sehari-hari ... 15

C) Aplikasi Turunan dalam Ekonomi ... 18

1) Aplikasi Turunan dalam Menghitung Biaya Total, Biaya Marginal dan Biaya Rata-Rata ... 18

2) Utilitas Total, Utilitas Marginal ... 20

BAB III ... 23

A. Kesimpulan ... 23

B. Saran ... 23

DAFTAR PUSTAKA ... 24

3

BAB I PENDAHULUAN

A. Latar Belakang

Matematika merupakan salah satu mata pelajaran pokok dalam kurikulum pendidikan di Indonesia, termasuk pada jenjang perguruan tinggi yang biasanya dimuat dalam Mata Kuliah Kalkulus, Statistika, atau yang lainnya. Menurut Johnson dan Rising (dalam Suherman, dkk, 2003 :17), bahwa matematika adalah pola pikir, pola mengorganisasikan, pembuktian yang nyata, matematika itu adalah bahasa yang menggunakan istilah yang didefinisikan dengan cermat, jelas, dan akurat, representasinya dengan symbol dan padat, lebih berupa bahasa symbol mengenai ide daripada mengenai bunyi. Sedangkan menurut Kline (dalam Suherman, dkk, 2003 : 17), matematika bukanlah pengetahuan menyendiri yang dapat sempurna karena dirinya sendiri tetapi adanya matematika itu terutama untuk membantu manusia dalam memahami dan menguasai permasalahan sosial, ekonomi dan alam. Sehingga dapat disimpulkan bahwa pada hakikatnya pembelajaran matematika menitikberatkan mengenai telaah tentang pola dan hubungan, suatu jalan atau pola berpikir, suatu seni, suatu bahasa yang representasinya berupa bahasa symbol mengenai ide untuk membantu manusia dalam memahami masalah sosial, ekonomi dan alam.

Kalkulus merupakan salah satu cabang ilmu matematika yang sering digunakan dalam kehidupan. Kalkulus (Bahasa Latin: calculus, artinya "batu kecil", untuk menghitung) adalah cabang ilmu matematika yang mencakup limit, turunan, integral, dan deret takterhingga.

Kalkulus adalah ilmu mengenai perubahan, sebagaimana geometri adalah ilmu mengenai bentuk dan aljabar adalah ilmu mengenai pengerjaan untuk memecahkan persamaan serta aplikasinya (Zam, 2013). Kalkulus memiliki aplikasi yang luas dalam bidang-bidang sains, ekonomi, dan teknik; serta dapat memecahkan berbagai masalah yang tidak dapat dipecahkan dengan aljabar elementer. Pada cabang ini terdapat bahasan yang paling sering digunakan dalam kehidupan yaitu Turunan. Turunan merupakan pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan turunan disebut diferensiasi.

4

Turunan sering kali digunakan dalam berbagai aspek kehidupan, contohnya dapat digunakan untuk menentukan kecepatan dan percepatan sehingga sering digunakan dalam pekerjaan dan penelitian yang membutuhkan ilmu fisika seperti menghitung laju percepatan pada kegiatan lempar lembing, lempar cakram, menembak, dan lain-lain. Turunan juga dapat digunakan dalam membuat konstruksi bangunan, percampuran bahan-bahan bangunan yang dilakukan oleh arsitek, pembuatan tiang-tiang, langit-langit, ruangan, dan lain-lain menggunakan turunan sehingga bangunan terlihat indah dan kokoh secara optimal. Selain itu, turunan juga dapat digunakan dalam bidang ekonomi seperti dalam upaya meminimalisir biaya produksi tanpa mengabaikan kualitas, memaksimumkan keuntungan, menghitung elastisitas prosuksi, utilitas, biaya total, biaya marginal, dan lain sebagainya.

B. Rumusan Masalah

1. Bagaimana Turunan digunakan dalam bidang Ekonomi?

2. Apa saja hal-hal pada bidang ekonomi yang dapat ditentukan/dihitung menggunakan Turunan?

C. Tujuan Penulisan

1. Untuk mengetahui penerapan turunan pada bidang ekonomi

2. Untuk mengetahui hal-hal pada bidang ekonomi yang dapat ditentukan/dihitung menggunakan rumus turunan.

5

BAB II PEMBAHASAN

A) Turunan

A. Konsep Turunan

Konsep turunan sejatinya bisa kita pahami dengan mengingat kembali konsep garis singgung, kecepatan rerata dan kecepatan sesaat, laju pertumbuhan dan lain-lain.

Perhatikan konsep garis singgung dibawah ini.

Misalkan terdapat grafik fungsi f(x) dimana grafik fungsi tersebut kontinu.

Kemudian terdapat suatu garis lurus yang memotong grafik fungsi f(x) di dua titik, yakni titik A dan B, seperti gambar berikut.

Gambar 1

Karena garis lurus memotong grafik fungsi di dua titik, maka garis tersebut disebut juga sebagai garis secan. Dari gambar, dapat diasumsikan bahwa garis secan mempunyai kemiringan atau gradien tertentu. Ingat kembali rumus gradien suatu garis yang memotong grafik fungsi di dua titik yang berbeda.

𝑚 =Δ𝑦

∆𝑥 = (𝑦₂− 𝑦₁) (𝑥₂− 𝑥₁)

Diketahui A (𝑥, 𝑓(𝑥)) dan B ((𝑥 + ℎ), 𝑓(𝑥 + ℎ)) maka dapat diketahui titik absis dan ordinatnya. Sehingga diperoleh gradien garis AB adalah sebagai berikut

6

𝑚 =𝑓(𝑥 + ℎ) − 𝑓(𝑥) 𝑥 + ℎ − 𝑥 𝑚 =𝑓(𝑥 + ℎ) − 𝑓(𝑥)

ℎ

Perhatikan gambar berikut.

(a) (b)

(c)

Gambar 2

Perhatikan ketiga gambar diatas. Jika 2 titik potong (A, B) pada garis lurus yang memotong grafik fungsi f(x) dibuat saling mendekati atau jarak antar titiknya dibuat mendekati nol maka garis itu lama kelamaan akan berubah menjadi garis yang memotong

7

grafik di 1 titik saja atau menjadi garis singung grafik. Sehingga dapat diperoleh gradien dari garis singung grafik adalah sebagai berikut.

𝑚 = lim⁡

ℎ→0

Δ𝑦

∆𝑥 𝑚_𝐴𝐵 = lim⁡

ℎ→0

𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ

Dengan syarat limitnya ada. Gradien garis singung inilah yang disebut sebagai turunan fungsi 𝑓(𝑥).

Perhatikan kasus mengenai kecepatan rerata dan kecepatan sesaat berikut ini.

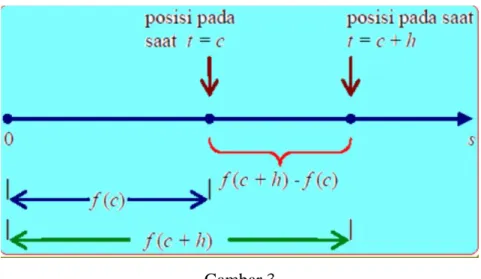
Gambar 3

Misalkan 𝑠 = 𝑓(𝑡) adalah persamaan gerak suatu benda sepanjang garis lurus, dengan⁡𝑡 adalah waktu, 𝑠 adalah jarak benda dari titik awal pada waktu t atau perpindahan benda dan f adalah gerakan fungsi posisi benda. Pada selang waktu 𝑡 = 𝑐 sampai 𝑡 = 𝑐 + ℎ, perubahan posisi 𝑓(𝑐 + ℎ) − 𝑓(𝑐) adalah seperti gambar 3. Sehingga dapt dihitung kecepatan reratanya adalah sebagai berikut.

𝐾𝑒𝑐𝑒𝑝𝑎𝑡𝑎𝑛⁡𝑟𝑒𝑟𝑎𝑡𝑎 = ⁡𝑝𝑒𝑟𝑝𝑖𝑛𝑑𝑎ℎ𝑎𝑛

𝑤𝑎𝑘𝑡𝑢 =𝑓(𝑐 + ℎ) − 𝑓(𝑐) ℎ

Untuk menghitung kecepatan untuk selang waktu yang sangat sempit atau kecil dimana h mendekati nol, maka dapat diperoleh kecepatan sesaat untuk 𝑡 = 𝑐 sebagai berikut.

𝐾𝑒𝑐𝑒𝑝𝑎𝑡𝑎𝑛⁡𝑠𝑒𝑠𝑎𝑎𝑡 = lim

ℎ→0

𝑓(𝑐 + ℎ) − 𝑓(𝑐) ℎ

8

Dengan syarat limitnya ada. Kecepatan sesaat inilah yang disebut sebagai turunan fungsi 𝑓(𝑡).

B. Definisi Turunan Definisi

Turunan fungsi 𝑓 adalah fungsi lain 𝑓′ yang nilainya pada sebarang bilangan riil adalah 𝑓^′(𝑥) = ⁡ lim⁡

ℎ→0

𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ

Dengan syarat limitnya ada untuk suatu bilangan riil x.

Tidak ada yang khusus dalam pemilihan huruf x, misal dipakai huruf c, a dan lainnya untuk menggantikan x itu sah-sah saja (tidak memberikan efek pada turunannya) atau huruf lain misal b untuk menggantikan h. Misal seperti berikut.

𝑓^′(𝑐) = ⁡ lim⁡

ℎ→0

𝑓(𝑐 + ℎ) − 𝑓(𝑐) ℎ

𝑓^′(𝑎) = ⁡ lim⁡

ℎ→0

𝑓(𝑎 + ℎ) − 𝑓(𝑎) ℎ

𝑓^′(𝑥) = ⁡ lim⁡

𝑏→0

𝑓(𝑥 + 𝑏) − 𝑓(𝑥) 𝑏

Jika diambil 𝑥 = 𝑐 + ℎ yang mengakibatkan ℎ = 𝑥 − 𝑐, maka dapat kita peroleh 𝑓^′(𝑐) = ⁡ lim⁡

ℎ→0

𝑓(𝑥) − 𝑓(𝑐) 𝑥 − 𝑐

Selain dapat ditulis dalam notasi 𝑓^′(𝑥), 𝑓^′(𝑐), 𝑓^′(𝑎) dan lain-lain, terdapat pula berbagai macam notasi dalam menuliskan turunan fungsi, diantaranya adalah sebagai berikut.

Turunan ke- Notasi Lagrange Notasi y Notasi Leibniz Notasi Euler

1 𝑓^′(𝑥) 𝑦′ 𝑑𝑦

𝑑𝑥

𝐷_𝑥𝑦

2 𝑓^′′(𝑥) 𝑦′′ 𝑑²𝑦

𝑑𝑥²

𝐷_𝑥²𝑦

3 𝑓^′′′(𝑥) 𝑦^′′′ 𝑑³𝑦

𝑑𝑥³

𝐷_𝑥³𝑦

n 𝑓^𝑛(𝑥) 𝑦^𝑛 𝑑^𝑛𝑦

𝑑𝑥^𝑛

𝐷_𝑥^𝑛𝑦

9 C. Aturan-Aturan Pencarian Turunan

Teorema

Keterdiferensiasian Mengimplikasikan Kekontinuan Jika 𝑓^′(𝑥)⁡ada maka 𝑓 kontinu di 𝑥

Teorema

Aturan Fungsi Konstanta

Jika 𝑓(𝑥) = 𝑘 dengan 𝑘 adalah konstanta maka untuk sebarang x, 𝑓^′(𝑥) = 0 Teorema

Aturan Fungsi Identitas

Jika 𝑓(𝑥) = 𝑥, maka 𝑓′(𝑥) = 1 Teorema

Aturan Pangkat

Jika 𝑓(𝑥) = 𝑥^𝑛 dengan 𝑛 bilangan bulat positif, maka 𝑓^′(𝑥) = 𝑛𝑥^𝑛−1 Teorema

Aturan Kelipatan Konstanta

Jika 𝑘⁡adalah suatu konstanta dan 𝑓 adalah suatu fungsi yang terdiferensialkan, maka (𝑘𝑓)^′(𝑥) = 𝑘𝑓′(𝑥)

Teorema

Aturan Jumlah

Jika 𝑓 dan 𝑔 adalah fungsi-fungsi yang terdiferensialkan, maka (𝑓 + 𝑔)′(𝑥) = 𝑓′(𝑥) + 𝑔′(𝑥)

Teorema

Aturan Selisih

Jika 𝑓 dan 𝑔 adalah fungsi-fungsi yang terdiferensialkan, maka (𝑓 − 𝑔)^′(𝑥) = 𝑓^′(𝑥) − 𝑔′(𝑥)

Teorema

Aturan Hasil Kali

Jika 𝑓 dan 𝑔 adalah fungsi-fungsi yang terdiferensialkan, maka (𝑓 ∙ 𝑔)^′(𝑥) = 𝑓′(𝑥)𝑔(𝑥) + 𝑓(𝑥)𝑔′(𝑥)

10 Teorema

Aturan Hasil Bagi

Jika 𝑓 dan 𝑔 adalah fungsi-fungsi yang terdiferensialkan, maka (^𝑓

𝑔)^′(𝑥) =

𝑓^′(𝑥)𝑔(𝑥)+𝑓(𝑥)𝑔^′(𝑥) (𝑔(𝑥))²

Teorema

Aturan Rantai

Misalkan 𝑦 = 𝑓(𝑢) dan 𝑢 = 𝑔(𝑥) dengan 𝑔 adalah fungsi yang terdiferensialkan di 𝑥 dan 𝑓 adalah fungsi yang terdiferensialkan di 𝑢, maka fungsi komposit 𝑓 ∘ 𝑔, didefinisikan oleh (𝑓 ∘ 𝑔)(𝑥) = 𝑓(𝑔(𝑥)) terdiferensialkan di 𝑥 dan (𝑓 ∘ 𝑔)′(𝑥) = 𝑓′(𝑔(𝑥))𝑔′(𝑥).

D. Turunan Fungsi Trigonometri

Dengan menggunakan definisi turunan, maka dapat diperoleh teorema trigonometri sebagai berikut.

𝐷_𝑥sin 𝑥 = cos 𝑥 𝐷_𝑥cos 𝑥 = −sin 𝑥

𝐷_𝑥tan 𝑥 = sec²𝑥 𝐷_𝑥sec 𝑥 = sec 𝑥 tan 𝑥

𝐷_𝑥cot 𝑥 = −csc²𝑥 𝐷_𝑥csc 𝑥 = −csc 𝑥 cot 𝑥

E. Penerapan Turunan dalam Kehidupan Sehari-hari

Berikut adalah penerapan turunan dalam kehidupan sehari-hari.

Proyek pembangunan suatu gedung dapat diselesaikan dalam 𝑥 hari dengan menghabiskan biaya proyek per-hari sebesar 3𝑥 − 180 +^5.000

𝑥 ratus ribu rupiah. Biaya minimum proyek pembangunan gedung tersebut adalah…

11 Jawab :

Misalkan 𝑓(𝑥) menyatakan biaya proyek selama 𝑥 hari dalam satuan ratus ribu rupiah sehingga

𝑓(𝑥) = 𝑥 (3𝑥 − 180 +5.000 𝑥 ) 𝑓(𝑥) = 3𝑥²− 180𝑥 + 5.000

Supaya biaya proyek minimum, nilai 𝑥 yang bersesuaian dapat ditentukan saat 𝑓^′(𝑥) = ⁡ lim⁡

ℎ→0

𝑓(𝑥+ℎ)−𝑓(𝑥)

ℎ = 0, yakni sebagai berikut.

𝑓^′(𝑥) = 6𝑥 − 180 6𝑥 − 180 = 0 6𝑥 = 180 𝑥 = 30

Dengan demikian, proyek tersebut harus diselesaikan dalam waktu 30 hari agar biaya proyeknya minimum. Maka biaya minimum yang harus dikeluarkan adalah

𝑓(𝑥) = 3𝑥²− 180𝑥 + 5.000

𝑓(30) = 3(30)²− 180(30) + 5.000 𝑓(30) = 2.700 − 5.400 + 5.000 𝑓(30) = 2.300

Jadi, biaya proyek minimum pembangungan gedung tersebut adalah 230 juta rupiah.

B) Nilai Maksimum dan Minimum Suatu Fungsi A. Nilai Maksimum dan Minimum Suatu Fungsi

Nilai maksimum dan minimum fungsi sejatinya adalah aplikasi atau penerapan dari konsep turunan. Nilai suatu fungsi dikatakan maksimum jika nilai dari fungsi tersebut paling besar dan sebaliknya nilai suatu fungsi dikatakan minimum jika nilai suatu fungsi tersebut paling kecil pada sebuah selang atau interval tertutup. Secara formal, nilai maksimum dan minimum suatu fungsi dapat dinyatakan sebagai berikut.

12 Definisi

Misal 𝑆 adalah daerah asal dari 𝑓 dan memuat titik 𝑐.

1. 𝑓(𝑐) adalah nilai maksimum dari 𝑓 pada 𝑆 jika 𝑓(𝑐) ≥ 𝑓(𝑥) untuk semua 𝑥 pada 𝑆 2. 𝑓(𝑐) adalah nilai minimum dari 𝑓 pada 𝑆 jika 𝑓(𝑐) ≤ 𝑓(𝑥) untuk semua 𝑥 pada 𝑆

Dari nilai maksimum dan nilai minimum suatu fungsi inilah dapat diperoleh nilai ekstrim. Pengaplikasian nilai ekstrim dalam kehidupan nyata sangat beragam, mulai dari untuk mencari biaya atau bahan minimum dalam proyek, mencari keuntungan maksimum, mencari volume maksimum dan lain hal sebagainya. Adapun definisi formal dari nilai ekstrim adalah sebagai berikut.

Definisi

Misal 𝑆 adalah daerah asal dari 𝑓 dan memuat titik 𝑐.

1. 𝑓(𝑐) adalah nilai ektrim dari 𝑓 pada S jika 𝑓(𝑐) adalah nilai maksimum atau nilai minimum

2. Fungsi yang akan dicari nilai ekstrimnya dikatakan fungsi objektif

Dalam menentukan nilai maksimum dan nilai minimum suatu fungsi di suatu selang tutup, dapat dicek terlebih dahulu apakah 𝑓 kontinu pada selang tutup tersebut.

Teorema

Jika 𝑓 kontinu pada selang tutup [𝑎, 𝑏] maka 𝑓 mencapai nilai maksimum dan nilai minimum pada selang tersebut.

Terdapat beberapa titik yang merupakan kandidat dimana suatu fungsi dapat bernilai maksimum dan minimum, yakni di titik ujung selang, di titik dimana turunan fungsinya sama dengan 0 atau yang biasa dikenal sebagai titik stasioner dan titik dimana fungsi tidak dapat diturunkan atau dikenal dengan titik singular. Kandidat-kandidat itulah yang disebut sebagai titik-titik kritis.

Teorema Titik Kritis

Misal 𝑓 didefinisikan pada interval 𝐼 yang memuat 𝑐. Jika 𝑓(𝑐) adalah nilai ekstrim, maka 𝑐 adalah titik kritis, yakni

1. Titik Ujung pada 𝐼

2. Titik Stasioner dari 𝑓, yaitu 𝑓^′(𝑐) = 0 3. Titik Singular dari 𝑓,⁡yaitu 𝑓^′(𝑐) tidak ada

13

Dari teorema diatas, maka secara langsung dapat ditentukan langkah-langkah dalam mencari nilai maksimum dan minimum suatu fungsi di selang tutup 𝐼 yaitu cari terlebih dahulu titik-titik kritis dari ⁡𝑓 pada selang 𝐼, kemudian carilah nilai 𝑓 pada titik-titik kritis yang sudah didapatkan, dan terakhir periksalah nilai 𝑓 yang paling besar dan nilai 𝑓 yang paling kecil. Nilai 𝑓 yang paling besar berarti nilai itu adalah nilai maksimum dari fungsi 𝑓 tersebut sedangkan nilai 𝑓 yang paling kecil berarti nilai itu adalah nilai minimum dari fungsi 𝑓 tersebut.

Definisi (Uji Ekstrim Lokal)

Misal 𝑆 adalah daerah asal 𝑓 dan 𝑐 ∈ 𝑆.

1. 𝑓(𝑐) nilai maksimum lokal 𝑓 pada 𝑆 jika terdapat selang buka 𝐼 yang memuat 𝑐 sedemikian hingga 𝑓(𝑐) ≥ 𝑓(𝑥), ∀𝑥 ∈ 𝐼 ∩ 𝑆

2. 𝑓(𝑐) nilai minimum lokal 𝑓 pada 𝑆 jika terdapat selang buka 𝐼 yang memuat 𝑐 sedemikian hingga 𝑓(𝑐) ≤ 𝑓(𝑥), ∀𝑥 ∈ 𝐼 ∩ 𝑆

3. 𝑓(𝑐) nilai ekstrim lokal 𝑓 pada 𝑆 jika 𝑓(𝑐) adalah nilai maksimum lokal atau minimum lokal

Dari definisi mengenai uji ekstrim lokal diatas, dapat diperoleh beberapa teorema terkait dengan nilai ekstrim lokal diantaranya yakni uji pertama untuk nilai ekstrim lokal dan uji kedua untuk nilai ekstrim lokal.

Definisi (Uji Pertama untuk Ekstrim Lokal)

Misal 𝑓 dapat didiferensialkan pada selang buka (𝑎, 𝑏)⁡yang memuat titik kritis 𝑐,

1. Jika 𝑓^′(𝑥) > 0⁡untuk semua 𝑥 ∈ (𝑎, 𝑐) dan 𝑓^′(𝑥) < 0⁡untuk semua 𝑥 ∈ (𝑐, 𝑏) maka 𝑓(𝑐) adalah nilai maksimum lokal

2. Jika 𝑓^′(𝑥) < 0⁡untuk semua 𝑥 ∈ (𝑎, 𝑐) dan 𝑓^′(𝑥) > 0⁡untuk semua 𝑥 ∈ (𝑐, 𝑏) maka 𝑓(𝑐) adalah nilai minimum lokal

3. Jika 𝑓^′(𝑥) bertanda sama untuk kedua pihak, maka 𝑓(𝑐) bukan nilai ekstrim Definisi (Uji Pertama untuk Ekstrim Lokal)

Misal 𝑓 dan 𝑓^′ dapat didiferensialkan pada selang buka (𝑎. 𝑏) yang memuat titik 𝑐 dengan 𝑓^′(𝑐) = 0

14

1. Jika 𝑓^′′(𝑐) < 0 maka 𝑓(𝑐) adalah nilai maksimum lokal 2. Jika 𝑓^′′(𝑐) > 0 maka 𝑓(𝑐) adalah nilai minimum local

B. Kemonotonan dan Kecekungan

Selain untuk mencari nilai maksimum dan nilai minimum, turunan juga dapat membantu kita dalam mencari apakah fungsi 𝑓 naik pada selang 𝐼 atau justru fungsi 𝑓 turun pada selang 𝐼. Definisi persis tentang naik dan turunnya suatu fungsi dapat dituliskan sebagai berikut.

Definisi

Misal 𝑓 didefinisikan pada interval 𝐼.

1. 𝑓 naik pada 𝐼 jika untuk setiap pasang bilangan 𝑥₁ dan 𝑥₂ dalam 𝐼 berlaku 𝑥₁ < 𝑥₂ ⇒ 𝑓(𝑥₁) < 𝑓(𝑥₂)

2. 𝑓 turun pada 𝐼 jika untuk setiap pasang bilangan 𝑥₁ dan 𝑥₂ dalam 𝐼 berlaku 𝑥₁ < 𝑥₂ ⇒ 𝑓(𝑥₁) > 𝑓(𝑥₂)

3. 𝑓 monoton murni pada 𝐼 jika 𝑓 naik pada 𝐼 atau turun pada 𝐼

Ingat bahwa konsep turunan dapat diperoleh dari konsep garis lurus yang memotong grafik di dua titik dan konsep garis singung. Perhatikan gambar dibawah ini.

Gambar 4

Dari gambar diperoleh informasi yaitu dimana 𝑓^′(𝑥) > 0 maka garis singgungnya bergerak naik sedangkan saat 𝑓^′(𝑥) < 0 garis singgungnya bergerak turun.

Teorema Kemonotonan

Misal 𝑓 dapat didefinisikan pada titik dalam selang 𝐼.

1. Jika 𝑓^′(𝑥) > 0 untuk semua titik dalam 𝑥 dari selang 𝐼 maka 𝑓 naik pada selang 𝐼

15

2. Jika 𝑓^′(𝑥) < 0 untuk semua titik dalam 𝑥 dari selang 𝐼 maka 𝑓 turun pada selang 𝐼 Kemonotonan suatu fungsi erat kaitannya dengan turunan pertama dari fungsi tersebut.

Sedangkan kecekungan suatu fungsi berkaitan dengan turunan kedua dari fungsi. Perhatikan definisi berikut ini.

Definisi

Misalkan 𝑓⁡dapat didiferensialkan pada selang buka 𝐼. Jika 𝑓′ naik pada 𝐼 dikatakan 𝑓⁡cekung ke atas di 𝐼 dan jika 𝑓′ turun pada⁡𝐼 dikatakan 𝑓 cekung kebawag di 𝐼.

Perhatikan bahwa turunan dari 𝑓′ adalah 𝑓′′. Sehingga dari definisi kecekungan diatas dapat diperoleh teorema kecekungan sebagai berikut.

Teorema Kecekungan

Andaikan 𝑓 terdiferensiasi dua kali pada interval terbuka 𝐼

1. Jika 𝑓^′′(𝑥) > 0 untuk semua 𝑥 dalam 𝐼, maka 𝑓 cekung ke atas pada 𝐼 2. Jika 𝑓^′′(𝑥) < 0 untuk semua 𝑥 dalam 𝐼, maka 𝑓 cekung ke bawah pada 𝐼

Dalam kasus-kasus tertentu, pada selang tertentu, suatu grafik fungsi 𝑓 dapat cekung keatas dan cekung kebawah dalam beberapa sub selang. Hal tersebut mengakibatkan adanya titik yang biasa dikenal dengan titik belok. Sebuah titik dikatakan sebagai titik belok dari grafik fungsi 𝑓 jika 𝑓 cekung keatas di satu sisi dari 𝑐 dan 𝑓 cekung kebawah di sisi lainnya dari 𝑐. Titik-titik dengan 𝑓^′′(𝑥) = 0 atau 𝑓^′′(𝑥) tidak ada dapat dijadikan kandidat titik belok suatu grafik fungsi.

C. Penerapan Nilai Maksimum dan Minimum dalam Kehidupan Sehari-hari

Berikut adalah contoh penerapan nilai maksimum dan minimum dalam kehidupan sehari- hari.

Contoh 1

Sebuah balok tanpa tutup dengan alas persegi (𝑥⁡. 𝑥) dan tinggi 𝑡 mempunyai volume 180⁡𝑐𝑚³.⁡Agar luas permukaan balok minimum, maka besar nilai 𝑥 adalah …

Jawab

Pertama-tama nyatakan 𝑡 dalam 𝑥 dengan menggunakan volume balok dengan alas persegi tersebut.

16 𝑉 = 108

𝑥⁡. 𝑥⁡. 𝑡 = 108 𝑥². 𝑡 = 108 𝑡 =¹⁰⁸

𝑥²

Dengan demikian dapat dinyatakan luas permukaan (𝐿) balok sebagai fungsi terhadap 𝑥 sebagai berikut.

𝐿(𝑥) = 4(𝑥⁡. 𝑡) + (𝑥⁡. 𝑥) 𝐿(𝑥) = 4𝑥𝑡 + 𝑥²

𝐿(𝑥) = 4𝑥¹⁰⁸

𝑥² + 𝑥² 𝐿(𝑥) = 432𝑥⁻¹+ 𝑥²

Luas permukaan akan miniumum saat 𝐿^′(𝑥) = 0 sehingga 𝐿^′(𝑥) = 0

−432𝑥⁻²+ 2𝑥 = 0 2𝑥 = 432𝑥⁻²⁡ 𝑥³ = 216 𝑥 = √216³ 𝑥 = 6

Jadi, besar nilai 𝑥 agar luas permukaannya minimum adalah 6 cm.

Contoh 2

Terdapat sebuah kawat dengan panjang 90 cm. Kawat tersebut akan dipotong menjadi 2 bagian, satu bagian untuk bahan membuat segitiga sama sisi dengan panjang 𝑥 cm dan satunya digunakan untuk membuat persegi. Agar jumlah luasnya maksimum, tentukanlah nilai 𝑥.

17 Jawab :

Diketahui segitiga sama sisi memiliki panjang sisi 𝑥, maka kawat yang dibutuhkan adalah 𝑥 + 𝑥 + 𝑥 = 3𝑥 cm. Sedangkan sisa kawat akan dijadikan bahan membuat persegi adalah (90 − 3𝑥) cm. Jadi 𝑆_{𝑝𝑒𝑟𝑠𝑒𝑔𝑖} = ^(90−3𝑥)

4

𝐿_{𝑝𝑒𝑟𝑠𝑒𝑔𝑖} = ^(90−3𝑥)

4 ⁡.^(90−3𝑥)

4

𝐿_{𝑝𝑒𝑟𝑠𝑒𝑔𝑖} = ^{(90−3𝑥)2}

16

Kemudian dapat diperoleh 𝐿_{𝑠𝑒𝑔𝑖𝑡𝑖𝑔𝑎} sebagai berikut.

𝐿_{𝑠𝑒𝑔𝑖𝑡𝑖𝑔𝑎} = ¹

2⁡. 𝑥⁡. 𝑥⁡. sin 60° = ⁡¹

4√3𝑥²⁡cm²

Setelah diketahui luas persegi dan luas segitiga, maka dapat ditulis fungsi 𝑓 sebagai berikut.

𝑓(𝑥) = ⁡^{(90−3𝑥)2}

16 + ⁡¹

4√3𝑥²⁡

Agar 𝑓(𝑥) maksimum, maka harus dibuat 𝑓^′(𝑥) = 0 𝑓^′(𝑥) = 0

(2)(90−3𝑥)(−3) 16 + ⁡¹

4√3(2)𝑥 = 0⁡

18𝑥−540 16 + ⁡²

4√3𝑥 = 0⁡

9𝑥 − 270 + ⁡4√3𝑥 = 0 9𝑥 + 4√3𝑥 = 270

𝑥 = ²⁷⁰

9+4√3 cm

Jadi, agar luasnya maksimum, nilai x yang tepat adalah 𝑥 = ²⁷⁰

9+4√3 cm.

18 C) Aplikasi Turunan dalam Ekonomi

1) Aplikasi Turunan dalam Menghitung Biaya Total, Biaya Marginal dan Biaya Rata- Rata

Dalam suatu proses produksi, akan sering disebut istilah biaya. Biaya yang digunakan untuk seluruh proses produksi dikatakan sebagai biaya total (total cost), sedangkan biaya yang digunakan untuk satuan unit produksi dikatakan sebagai biaya rata-rata (average cost). Biaya total sendiri terdiri dari total biaya tetap ditambah dengan biaya variabel. Secara metematis ditulis sebagai berikut.

𝑇𝐶 = 𝐹𝐶 + 𝑉𝐶 dengan : 𝑇𝐶 = biaya total (total cost)

𝑉𝐶 = biaya variabel (variable cost) 𝐹𝐶 = biaya tetap (fixed cost)

Biaya total adalah fungsi dari kuantitas barang yang diproduksi, dimana besarnya biaya total adalah hasil kali antara banyaknya barang yang diproduksi dengan biaya rata- rata barang per-unit. Fungsi tersebut dapat dituangkan menjadi sebagai berikut.

𝑇𝐶 = 𝑓(𝑄) + 𝑘 dengan : 𝑇𝐶 = biaya total (total cost)

⁡⁡𝑄 = kuantitas barang yang diproduksi (quantity)

Perhatikan bahwa 𝑇𝐶 = 𝑓(𝑄) + 𝑘, dimana 𝑓(𝑄) = 𝑉𝐶 adalah biaya variabel yang akan berubah menurut jumlah barang yang diproduksi. Hal ini dikarenakan variable cost akan selalu berubah-ubah sesuai dengan suatu kondisi yang terjadi dalam suatu unit kegiatan, misalnya volume produksi ataupun kondisi yang lain. Sedangkan 𝑘 = 𝐹𝐶 akan selalu konstan selama jangka tertentu karena 𝐹𝐶 atau fixed cost adalah biaya tetap dalam suatu unit kegiatan. Biaya ini tidak akan mengalami perubahan walaupun terjadi pengangguran atau penambahan produksi (misalnya dalam kegiatan produksi) sehingga untuk fungsi semacam ini dikenal dengan istilah fungsi konstan.

19

Fungsi biaya secara keseluruhan dapat dibagi kedalam beberapa jenis yakni : a. Linear : 𝑇𝐶 = 𝑎 + 𝑏𝑥, dengan 𝑎, 𝑏 > 0

b. Kuadratis : 𝑇𝐶 = 𝑎𝑥² + 𝑏𝑥 + 𝑐, dengan 𝑎, 𝑏, 𝑐 > 0

c. Kubik : 𝑇𝐶 = 𝑎𝑥³ + 𝑏𝑥²+ 𝑐𝑥 + 𝑑, dengan 𝑎, 𝑏, 𝑐, 𝑑 > 0

d. Eksponensial : 𝑇𝐶 = 𝑎⁡. 𝑒𝑏𝑥, dengan 𝑎, 𝑏 > 0, 𝑏 adalah tingkat pertumbuhan pada fungsi naik secara eksponensial

Selain biaya total, dapat dihitung pula biaya marginal dari suatu kegiatan produksi.

Biaya marginal adalah biaya yang diakibatkan adanya tambahan satu unit barang produksi. Secara matematik, fungsi biaya marginal adalah derivative pertama dari fungsi biaya total. Misal 𝑇𝐶(𝑄)⁡adalah biaya total yang dikeluarkan sebuah perusahaan untuk menghasilkan 𝑄 satuan barang tertentu. Fungsi 𝑇𝐶 disebut sebagai fungsi biaya. Jika banyaknya barang yang dihasilkan bertambah dari 𝑄₁ menjadi 𝑄₂ maka biaya tambahan yang dibutuhkan adalah 𝑇𝐶(𝑄₂) − 𝑇𝐶(𝑄₁). Limit besaran ini ketika x→0 disebut laju perubahan sesaat biaya, terhadap banyaknya barang yang dihasilkan atau biasa disebut juga dengan biaya marginal. Terakhir yakni biaya rata-rata. Biaya rata-rata adalah hasil bagi biaya total dengan kuantitas barang yang diproduksi. Sehingga dapat diperoleh.

𝐴𝐶 =𝑇𝐶 𝑄 Contoh Kasus

Fungsi Biaya Total sebuah perusahaan manufaktur adalah 𝑇𝐶 = 𝑓(𝑄) = 6700 + 4,15𝑄 + 30𝑄¹² rupiah. Carilah biaya rata-rata barang tiap unit dan biaya marginal barang bila perusahan akan memproduksi barang sebanyak 400 unit.

Jawab :

Biaya Total = 𝑓(𝑄) = 6700 + 4,15𝑄 + 30𝑄¹² Biaya Rata-rata = 𝐴𝐶 =^𝑇𝐶

𝑄 =6700+4,15𝑄+30𝑄¹²⁡ 𝑄

Biaya Marginal = ^𝑑𝐶

𝑑𝑄= 4,15 + 15𝑄⁻¹²

20

Sehingga jika perusahaan akan memproduksi barang sebanyak 400 unit, biayanya akan menjadi sebagai berikut.

Biaya Rata-rata = 𝐴𝐶 =6700+4,15(400)+30(400)¹²⁡

(400) =^8960⁡

400 = 22,4 perunit Jadi Biaya Rata-rata = 22,4 × 400 = 8960

Biaya Marginal = 4,15 + 15(400)⁻¹² = 4,15 + 0,75 = 4,9 Jadi Biaya Marginal = 4,9 × 400 = 1960

Dengan demikian berarti rata-rata biaya tiap satuan adalah Rp. 8960 untuk memproduksi 400 satuan yang pertama, untuk memproduksi satu satuan tambahan dia atas 400 hanya memerlukan biaya Rp.1960.

2) Utilitas Total, Utilitas Marginal

Fungsi utilitas adalah fungsi yang menjelaskan besarnya utilitas (kepuasan, kegunaan) yang diperoleh seseorang dari mengkonsumsi suatu barang atau jasa. Pada umumnya semakin banyak suatu barang dikonsumsi semakin besar utilitas yang diperoleh, kemudian mencapai titik puncaknya (titik jenuh) pada jumlah konsumsi tertentu, sesudah itu justru menjadi berkurang atau bahkan negatif jika jumlah barang yang dikonsumsi terus menerus ditambah.

Utilitas total ialah fungsi dari jumlah barang yang dikonsumsi. Dinyatakan dengan 𝑈 = 𝑓(𝑄)

Fungsi utilitas marginal adalah utilitas tambahan yang diperoleh dari setiap satu unit barang yang dikonsumsi. Fungsi utilitas marginal merupakan turunan pertama dari fungsi utilitas total. Jika fungsi utilitas total adalah 𝑈 = 𝑓(𝑄) maka utilitas marginalnya adalah

21 𝑀𝑈 = ⁡𝑑(𝑈)

𝑑𝑄 = 𝑈′

Gambar 5

Grafik Bentuk Kurva Utilitas

Contoh Kasus

Fungsi utilitas dinyatakan dalam persamaan 𝑈 = 15𝑄 − 5𝑄² Tentukanlah

a. Persamaan utilitas marginal serta berapa titik ekstrim dari fungsi utilitas totalnya b. Berapa utilitas marginal jika barang yang diproduksi ditambah dari 2 unit menjadi

3 unit Jawab :

a. 𝑈 = 15𝑄 − 5𝑄²

𝑀𝑈 = 𝑈^′= 15 − 10𝑄

𝑈 maksimum jika 𝑀𝑈 = 0⁡⁡→⁡⁡15 − 10𝑄 = 0⁡→⁡𝑄 =¹⁵

10= 1,5 Untuk 𝑄 = 1,5⁡maka

𝑈 = (15⁡𝑥⁡1,5) − 5⁡𝑥⁡1,5² = 22,5 − 11,25 = 11,25

22

b. 𝑗𝑖𝑘𝑎⁡𝑄 = 2⁡⁡⁡⁡⁡⁡→⁡⁡⁡⁡⁡⁡𝑀𝑈 = 15 − 10(2) = ⁡ −⁡5 𝑗𝑖𝑘𝑎⁡𝑄 = 3⁡⁡⁡⁡⁡⁡→⁡⁡⁡⁡⁡⁡𝑀𝑈 = 15 − 10(3) = ⁡ −15

Jadi, titik ekstrim fungsi utilitas total berada pada koordinat (1.5; 11,25). Pada saat konsumen mengkonsumsi 2 unit barang utilitas tambahan sudah menurun dan akan semakin menurun jika ditambah 1 unit lagi, sehingga konsumen harus mengurangi konsumsi terhadap produk tersebut untuk meningkatkan kembali utilitas tambahannya.

23 BAB III PENUTUP

A. Kesimpulan

Turunan merupakan pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukan. Tidak hanya sebagai salah satu materi pembelajaran semata, turunan dapat diaplikasikan dalam kehidupan manusia diberbagai bidang yang ada. Contohnya pada bidang ekonomi. Pengaplikasian ini ditujuankan tidak lain adalah agar dapat menyelesaikan permasalahan dengan cara yang lebih mudah dan praktis.

Pada bidang ekonomi penggunaan turunan berkaitan erat tentang perhitungan biaya total, biaya marginal dan biaya rata-rata suatu proses produksi. Biaya total adalah biaya yang diperlukan untuk memproduksi sejumlah barang tertentu, sedangkan biaya marginal adalah biaya tambahan yang dikeluarkan untuk menghasilkan satu unit tambahan produk.

B. Saran

1. Bagi para para pembaca menjadi dapat mempelajari juga aplikasi turunan di selain pada bidang ekonomi, misalnya pada bidang fisika, teknik, biologi, dan lain sebagainya.

2. Untuk teori pembahasan dapat mencari referensi-referensi dari sumber lainnya yang dapat menambah wawasan dan memperkuat argumen atau uraian yang sudah dituliskan.

24

DAFTAR PUSTAKA

Ammariah, Hani. 2020. “Cara Mencari Kemiringan (Gradien) Pada Garis Lurus”,

https://www.ruangguru.com/blog/matematika-kelas-8-3-cara-mencari-kemiringan-garis-lurus diakses pada 12 Desember pukul 20.31 WIB.

Ammariah, Hani. 2021. “Memahami Konsep Turunan Fungsi Aljabar”,

https://www.ruangguru.com/blog/turunan-fungsi-aljabar diakses pada 12 Desember 2021 pukul 21.01 WIB.

Blog KoMa. Kecepatan dan Percepatan Menggunakan Turunan. konsep-matematika.com.

https://www.konsep-matematika.com/2015/12/kecepatan-dan-percepatan-menggunakan.html diakses pada tanggal 12 Desember 22.12 WIB.

Suherman, E., Turmudi, Suryadi, D., Herman, T., Suhendra, Prabawanto, S., Nurjanah, dan Rohayati, A. 2003. Strategi Pembelajaran Matematika dan Kontemporer. Bandung : JICA- Universitas Pendidikan Indonesia (UPI).

Sukardi. 2019. “Soal dan Pembahasan – Aplikasi Turunan (Diferensial)”,

https://mathcyber1997.com/soal-dan-pembahasan-aplikasi-turunan-diferensial/ diakses pada tanggal 13 Desember 18.51 WIB.

Zam, Nizam. 2013. Sejarah dan Pengertian Kalkulus. Bandung: Institut Teknologi Bandung (ITB)