mekanika dan bahan dan 1

GEFIE & TIMDSHENKD

MEKANIKA

E3AHA N

MEKANIKA

BAHAN

JILID 1

JAMES M. GERE

Profesor Emeritus Stanford University

STEPHEN P. TIMOSHENKO (1878-1972)

Mantan Dosen Stanford University

�

PENERRIT ERL4NGGA

DAFTAR ISI

Pengantar ix

Simbol xm

Huruf Yunani xvi

TAR I K TEKAN DAN GESER 1

1 .1 1 .2 1 .3 1 .4 1 .5 1 .6 1 .7 1 .8

Pengantar

Tegangan dan Regangan Normal 3

Besaran Mekanis Bahan 9

Elastisitas, Plastisitas, dan Rangkak 1 8

Elastisitas Linier, hukum Hooke, dan Rasio Poisson

Tegangan dan Regangan Geser 26

Tegangan Izin dan Beban Izin 35 Desain untuk Beban Aksial dan Geser Langsung

Soal-soal 44

ELEMEN STRU KTUR YANG DIBEBANI SECARA AKSIAL

2.1 Pengantar 60

20

40

60

2.2 Perubahan Panjang pada Elemen Struktur yang Dibebani Secara

Aksial 6 1

2.3 Perubahan Panjang Batang yang Tidak Seragam 68

2.4 Struktur Statis Tak Tentu 74

2.5 Efek Termal 84

2.6 Tegangan pada Potongan Miring 9 1

2.7 Energi Regangan 1 00

*2.8 Beban Kejut 1 1 1

*2.9 Beban Berulang dan Fatik 1 20

*2.1 0 Konsentrasi Tegangan 1 23 *2.1 1 Perilaku Nonlinier 1 28 *2.1 2 Analisis Elastoplastis 134

Soa/-soal 138

TORSI 167

3.1 Pengantar 1 6 7

3.2 Deformasi Torsional Batang Lingkaran 1 68

3.3 Batang Lingkaran dari Bahan yang Elastis Linier 1 7 1 3.4 To rsi Tak Seragam 1 80

3.5 Tegangan dan Regangan pacta Geser Murni 1 86 3.6 Hubungan antara Modulus Elastisitas E dan G 1 92 3.7 Penyaluran Daya oleh Batang Lingkaran 193 3.8 Elemen Struktur Torsional Statis Tak Tentu 197 3.9 Energi Regangan pacta Kondisi Torsi dan Geser Murni 200

3.1 0 Tabung Berdinding Tipis 207

*3.1 1 Konsentrasi Tegangan dalam Keadaaan Torsi 214 *3.1 2 Torsi Nonlinear pacta Batang Lingkaran 2 1 6

Soal-soal 220

GAYA G ESER DAN MOMEN LENTUR

4.1 Pengantar 236

236

4.2 Jenis-jenis Balok, Beban, dan Reaksi 236 4.3 Gaya Geser dan Momen Lentur 240

4.4 Hubungan antara Beban, Gaya Geser, dan Momen Lentur 246 4.5 Diagram Gaya Geser dan Momen Lentur 250

Soal-soal 258

5

I

TEGANGAN Dl BALOK (TOPIK DASA R)

5.1 Pengantar 266

266

5.2 Lentur Murni dan Lentur Tak Seragam 267 5.3 Kelengkungan Balok 267

5.4 Regangan Longitudinal di Balok 269

5.5 Tegangan Normal di Balok (Bahan Elastis Linier) 272 5.6 Desain Balok terhadap Tegangan Lentur 28 1

5.7 Balok Nonprismatis 288

5.8 Tegangan Geser di Balok dengan Penampang Persegi Panjang 29 1 5.9 Tegangan Geser di Balok dengan Penampang Lingkaran 300 5.1 0 Tegangan Geser di Badan Ba1ok yang mempunyai Flens 30 I 5.1 1 Balok Tersusun dan Aliran Geser 306

5.1 2 Balok dengan Beban Aksial 309

5.1 3 Konsentrasi Tegangan pacta Kondisi Lentur 3 1 5

Soal-soal 317

I

TEGANGAN Dl BALOK (TOPI K LANJUT)

6.1 6.2 6.3 6.4 6.5

Pendahuluan 340

Balok Komposit 340

Metode Penampang Tertransformasi

Balok Simetris Ganda dengan Beban Miring Lentur pacta Balok Tak Simetris 358

340

348

•f

Mekanika Bahan _vii

6.6 Konsep Pusat Geser 365

6.7 Tegangan Geser di Balok dengan Penampang Terbuka di Dinding

Tipis 367

6.8 Pusat Geser Penampang Terbuka Berdinding Tipis 373

6.9 Lentur Elastoplastis 380 6.1 0 Lentur Nonlinier 388

Soal-soal 395

R eferensi dan Catatan Sejarah 410 Lampiran A Sistem dan Faktor Konversi

A.1 A.2 A.3 A.4 A.5

Sistem Satuan Satuan SI

4 1 8 4 1 9 Satuan Umum Amerika Serikat Satuan Temperatur 427

Konversi anta�;a Satuan

Lampiran B Pemecahan Soal

B .1 Jenis Soal 431

425

428

431

B.2 Langkah-langkah Pemecahan Soal 432

B.3 Homogenitas Dimensional 433

B.4 Angka Penting 434

B.5 Pembulatan Bilangan 436

Lampiran C R umus-rumus Matematika Lampiran D Be sa ran Luas Bidang

Lampiran E Besaran Profil Baja Struktural Lampiran F Besaran Kayu Struktural Lampiran G Defleksi dan Kemiringan Balok Lampiran H Besaran Bahan 460

Jawab Soal 465

437 441

453 418

PENGANTAR

Dengan mengambil mata kuliah mekanika bahan, mahasiswa mempelajari topik teknik dasar sekaligus juga mengembangkan kemampuan analitis dan pemecahan masalah. Selama persiapan Edisi Keempat ini, penulis selalu mengingat tuj uan-tujuan tersebut. Fakta-fakta dan teori-teori mekanika disajikan sedemikian rupa sehingga m udah dalam proses belajar mengajar, dengan pembahasan yang mendalam dan contoh yang banyak, supaya mahasiswa dapat segera menguasai suatu pokok bahasan. Selain itu, penekanan diberikan pada bagaimana menganalisis sistem mekanis dan struktural, dan banyak soal yang mengharuskan mahasiswa melakukan pemikiran orisinal.

Buku ini meliputi semua topik dasar mengenai mekanika bahan, yang disajikan pada level yang cocok untuk mahasiswa teknik tingkat dua dan tiga. Topik-topik utama adalah analisis dan desain elemen struktural yang mengalami tarik, tekan, torsi, dan lentur, termasuk konsep-konsep dasar seperti tegangan, regangan, perilaku elastis, perilaku inelastis, dan energi regangan. Topik-topik lain yang menarik adalah transformasi tegangan dan regangan, pembebanan gabungan, konsentrasi tegangan, defleksi balok, dan stabilitas kolom. Topik-topik yang lebih khusus adalah efek termal, pembebanan dinamis, elemen nonprismatis, balok dua bahan, pusat geser, bejana tekan, dan balok statis tak tentu. Untuk kelengkapan dan rujukan kerja, topik-topik dasar seperti gaya geser, momen lentur, pusat berat, dan momen inersia juga disajikan di dalam buku ini.

Buku ini membahas materi yang jauh lebih banyak daripada yang dapat dibahas dalam satu mata kuliah sehingga dose n mempu nyai kesempatan untuk memilih topik yang menurutnya paling mendasar dan relevan. Topik-topik lanjut di dalam suatu subbab diberi kode bintang (*).

Dosen juga dapat memanfaatkan ratusan soal baru (dengan total lebih dari 1 100 soal) yang tersedia sebagai pekerjaan rumah dan diskusi ke\as. Soa\­ soal diletakkan di akhir setiap bab agar mudah dicari dan tidak menyela penyajian suatu bab. (Soal yang sangat sulit atau panjang diberi kode satu atau lebih tanda bintang di dekat nomor soal.)

Mekanika Bahan ix

Pembahasan tentang kedua sistem dan tabel faktor konversi diberikan dalam lampiran. Untuk soal-soal dengan solusi numerik, soal bernomor ganjil menggunakan satuan uses dan soal bernomor genap menggunakan satuan SI. Satu-satunya pengecualian adalah pada soal dan contoh yang melibatkan tabel besaran untuk profil baja strnktural karena tabel untuk profil ini hanya tersedia dalam satuan uses. Jawaban soal dicantumkan di bagian belakang buku ini, sehingga mahasiswa dapat memeriksa hasil pekerjaannya.

Rujukan dan catatan sejarah juga dikumpulkan di bagian belakang buku ini. Rujukan dan catatan ini terdiri atas sumber asli pokok bahasan dan catatan biografis mengenai insinyu r, ilmuwan, dan matematikawan pelopor yang menemukan pokok bahasan mekanika bahan. Indeks nama yang terpisah akan mempermudah pencarian masing-masing tokoh sejarah ini. Buku ini dirampungkan dengan indeks subjek yang dipersiapkan secara ekstensif dan hati-hati sehingga setiap topik, konsep, kata kunci, atau definisi dapat ditemukan dengan cepat.

Edisi Keempat dari Mekanika Bahan ini telah ditulis ulang secara hati-hati dengan diskusi yang diperluas, tokoh-tokoh barn, contoh-contoh dan soal-soal barn, serta banyak pernbahan dalam pengaturannya agar buku ini lebih berguna di dalam ruangan kelas. Semua pernbahan dalam pengaturan dan penyajian ini diajukan oleh para dosen dan mahasiswa yang telah mengenal baik Edisi Ketiga.

Usaha yang keras telah dilakukan dalam memeriksa dan membaca ulang teks agar dapat menghilangkan kesalahan, namun apabila pembaca menemukannya, betapapun kecilnya, beritahulah penulis di Department of Civil Engineering, Stanford University, Stanford, California 94305-4020, U.S .A. (email jgere@ci-ve.stanford.edu), atau kontaklah penerbit (semua surat akan dibalas).

• Penghargaan

Edisi pertama buku ini, diterbitkan pada tahun 1972 dan ditulis o1eh penulis sekarang, mernpakan pengembangan dari buku terdahulu yang disusun oleh Profesor Stephen P. Timoshenko ( 1878-1972), yang menggunakan judul Strength of Materials. Timoshenko adalah perintis yang paling dihormati dalam bidang mekanika terapan. Melalui penelitian dan buku­ bukunya, ia merevolusi cara pengajaran mekanika, bukan hanya di Amerika Serikat melainkaQ juga di selurnh dunia. (Pembaca dapat menemukan biografi ringkas dari Timoshenko di dalam rnjukan pertama di bagian belakang buku ini.)

komentar dan ide yang berguna yang disumbangkan oleh Thalia Anagnos dari San Jose State University, John Burgess dari University of Hawaii , dan Aron Zaslavsky dari Technion.

Penelaah berikut ini telah membaca kesel uruhan Edisi Keempat dalam bentuk konsep dan telah memberikan baik komentar umum maupun khusus untuk perubahan dan perbaikan. Saran-saran mereka terbukti s angat berguna, dan penulis sangat menghargai telaahan dan ketelitian mereka. Terima kasih penulis sampaikan kepada: Majid R. Chitsaz dari Pennsyl­ vania State U niversity; Robert D. Cook dari Uniwrsit;. of Wisconsin­ Madison; Janak Dave dari University of Cincinnati; Sergey Drabkin dari Polytechnic U niversity of New York; Raghu Echempati dari Cni\'ersity of Mississippi; Harvey Lipkin dari Georgia Institute of Technolog;.: Douglas Nims dari University of Toledo; Douglas B. Rigby dari Hong Kong University of S cience adn Technology; dan P.D. S carlatos dari Florida Atlantic U niversity.

Selain itu, penelaah berikut ini telah memberikan komentar terhadap

Edisi Ketiga dalam telaah sebelum perbaikan. Saran-saran mereka sangat menentukan dalam pembe ntukan Edisi Keempat, dan pen ulis sangat menghargai ide-ide mereka. Terima kasih penulis sampaikan kepada: Hojjat Adeli dari Ohio State University; Kevyan Ahdut dari Uni\ ersity of the District of Colu mbia; John B. Brunski dan Robert H. P. Dunn, keduanya dari Rensselaer Polytechni c Institute; Ted A. Conway dari University of Akron ; Xiao mi n Deng dari University of So uth Carolina; Arya Ebrahimpour dari Pennsylvania S tate Universi ty; M. Elgaaly dan Anisur Rahman, keduanya dari Drexel University; Ahmed lbrahim dari S tate University of New York at Farmi ngdal e: Norman F. Knig ht dan Ramamurthy Prabhakaran , keduanya dari Old Dominion University; Gladius Lewis dari University of Memphis. Zhong Ming Liang dari Purdue Uni versity; E.L. Parker dari Valley Forge Mil itary Colege; Edwin Powers dari Catonsv ille Community College: Charles Rondeau dari Jamestown Community College; Michael Schwartz dari University of St. Thomas; Sheri Sheppard dari S tanford; R. S ierakowski dari Ohio S tate University; L.T.D. Topoleski dari University of Maryland at Baltimore; Morteza Torkamani dari University of Pittsburgh, dan Manoochehr Zoghi dari University of Dayton.

Pen ul i s dibantu dalam pengolahan kata (word processing) dan persiapan naskah, pembacaan ulang oleh Due Wong, yang telah bekerja dengan perhatian dan ketelitian penuh. Selain i tu, mahasiswa pascasarjana berikut ini telah memberikan bantuan keahliannya dalam membaca ulang dan menyiapkan solusi soal: Yih-Lin S helley Cheng, K rista Marie Donaldson, Denise M. Fennell, Jamie Hsieh, Peter I . Huang, Chao-Hua (Eric) Lin, Angela Chia-Lin Teng, dan May Min-Chiao Wong.

Penyuntingan dan produksi dilaksanakan secara trampil dan efisien oleh s taf PWS Publishing Company, termas uk Jonathan Plant, Mary Thomas Stone, dan Helen M. Walden. Penulis secara khusus berterima kasih pada Mary Thomas Stone, yang merupakan penyunting untuk buku ini dan memberikan komentar, pandangan, dan bantuan yang jauh melebihi yang penulis duga. Semangat bekerja sama dan bersahabat yang di tunjukkan oleh semuanya di PWS menjadikan pekerjaan i ni suatu kebahagiaan .

Mekanika Bahan x i

Kepada masing-masing orang baik ini, penulis dengan gembira menyampaikan penghargaan yang setinggi-tingginya.

James 1\1. Gere

• Alat Bantu Tambahan

Edisi Keempat menyertakan juga disket 3.5" yang mengandung program komputer yang berguna dan mudah-Mathcad™ Engine 5.0 for Win­ dows©-dan sekumpulan lembar kerja untuk memecahkan soal-soal mekanika bahan. Lembar kerja tersebut diperiksa silang terhadap contoh­ contoh dan soal-soal teks yang sesuai dengan ikon bergambar disket. Ikon ini menunjukkan jenis soal atau contoh yang sesuai dengan Jembar kerja tersebut. Semua soal dan contoh di dalam teks dimaksu dkan untuk dipecahkan sesuai pilihan dosen dan mahasiswa dan tidak didesain untuk perangkat hitung tertentu.

Juga tersedia paket baru yang unik berupa buku kerja dan CD-ROM,

Visual Mechanics. Dikembangkan di University of Washington oleh Ore­ gory R. Miller dan Stephen C. Cooper, paket ini terdiri atas CD-ROM dengan dua program (disebut Dr. Beam dan Dr. Stress), dan sebuah buku pegangan dengan lembar kelja, latihan, dan contoh-contoh, yang terpusat pada lentur balok dan analisis kondisi tegangan. Perangkat lunak dan bahan instruksional pendukungnya memberikan mahasiswa laboratorium virtual yang mudah dipakai untuk memvisualisasikan perilaku balok, memahami model matematika, dan mengeksplorasi teori mekanika bahan dan metode desain.

Kedua alat bantu yang didasarkan atas perangkat lunak ini ditujukan sebagai pelengkap; buku teks ini dapat digunakan dengan efektif secara tersendiri.

Instructor's Solution Manual dengan solusi lengkap untuk semua soal tersedia untuk pengguna buku ini.

SIMBOL

A A,. Aw a, b, c

c

c

D d

E E, E, e

F

f fr

G g H h

l,, / v' /: /<1, /�'� /n, ld\'l t, /1, l2 J K

Luas/area/daerah Luas sayap (jlens) Luas badan (web) Dimensi (ukuran), jarak

Pusat berat (centroid), konstanta integral, gaya tekan Jarak dari sumbu netral ke permukaan luar balok Diameter

Diameter, dimensi , ukuran jarak (distance) Modu lus elastisitas

Modulus elastisitas reduksi Modulu s elastisitas tangensial

Eksentrisitas, dimensi (ukuran), jarak, perubahan volume satuan (dilatasi)

Gay a

Aliran geser, faktor bentuk untuk lentur plastis, tleksibi litas, frekuensi (Hz)

Fleksibilitas torsional batang

Modu lus elastisitas dalm kondi si geser Percepatan gravitasi

Tinggi, jarak, gaya, reaksi , tenaga kuda Tinggi, dimensi (ukuran)

Momen inersia (atau momen kedua) dari sebuah luas bidang Momen inersia terhadap sumbu _{x, y,} dan z

Momen inersia terhadap sumbu _x1 dan y1 (su mbu diputar) Perkalian (produk) inersia terhadap sumbu xy

Perkalian (produk) inersia terhadap sumbu x1y1 (sumbu diputar) Momen inersia polar

Momen inersia utama Konstanta torsi

Faktor konsentrasi tegangan, modulus e\astisitas padat (bulk),

n

Konstanta pegas, kekakuan, simbol untuk El

Kekakuan torsional sebuah batang Panjang j arak

Panjang efektif sebuah kolom Logaritma natural (basis e) Logaritma umum (basis 10) Momen lentur, kopel, massa Momen plastis untuk sebuah balok Momen luluh untuk sebuah balok Beban kritis untuk sebuah kolom Beban plastis untuk sebuah struktur

Beban modulus-reduksi untuk sebuah kolom Beban modulus tangensial untuk sebuah kolom Beban luluh untuk sebuah struktur

Tekanan (gaya per satuan luas)

Gaya beban terpusat, momen pertama sebuah bidang Intensitas beban terdistribusi (gaya per satuan jarak) Reaksi; jari-jari (radius)

Jari-jari (radius), jari- jari girasi (gyration) El

Modulus potongan penampang sebuah balok, pusat geser Jarak, jarak di sepanjang sebuah garis lengkung

Gay a tarik; momen puntir atau momen putar (torque), temperatur Momen putar (torque) plastis

Momen putar (torque) luluh Tebal; waktu; intensitas torque Tebal sayap (jlens)

Tebal badan (web) Energi regangan

Densitas energi regangan ( energi re gang an per satuanvolume) Modulus resistansi

Modulus ketangguhan Gaya geser; volume

defleksi sebuah balok; kecepatan

dv/dx, d2v!d:2, dst.

a

Sudut, koefisien ekspansi panas, rasio nondimensional Sudut, rasio nondimensional, konstanta pegas, kekakuan Kekakuan p utar sebuah pegas

Regangan geser, densitas/rapat berat (berat per satuan volume) Regangan geser pada bidang xy, y.:, dan zx

Regangan geser terhadap sumbu x1y1 (sumbu diputar) Regangan geser untuk sumbu miring

Defleksi, pelepasan, perpanjangan sebuah batang atau pegas Beda temperatur

Pelepasan statis Pelepasan l ul uh Regangan normal

Regangan geser dalam arah x, y, dan z

Regangan normal untuk sumbu miring Regangan normal utama

Regangan lateral

Regangan luluh

Sudut-sudut rotasi sumbu balok, laj u puntiran sebuah batang dalam keadaan torsi (sudut puntir per satuan panjang ) Sudut terhadap sebuah bidang utama atau terhadap sebuah sumbu utama

S udut terhadap sebuah bidang tegangan geser maksimum Kelengkungan (K" = lip)

Jarak

Rasio Poisson

Jari-jari radius kelengkungan, jarak radial dalam koordinat po­ lar, massa jenis (massa per satuan volume)

Tegangan normal

Tegangan normal pacta bidang yang tegak lurus terhadap sumbu x, y, dan z

Tegangan normal pacta bidang yang tegak lurus terhadap sumbu x1y1 (sumbu diputar)

Tegangan normal pacta bidang miring Tegangan normal utama

Tegangan sisi (atau tegangan kerja)

Tegangan kritis untuk sebuah kolom (acr = Pc/A)

Tegangan geser pacta bidang yang tegak lurus terhadap sumbu

x, y, z, dan bekerj a sejajar sumbu y, z, dan x

Tegamgam geser pacta sebuah bidang yang tegak lurus terhadap sumbu x1 dan yang bekerja sejajar sumbu y1 (sumbu diputar) Tegangan geser pacta sebuah bidang miring

•

ru tegangan ultimate pada kondisi geser

ry tegangan luluh pada kondisi geser

Mekanika Bahan XV

cp sudut, sudut puntir sebuah batang pada kondisi torsi

IJ' sudut, sudut rotasi

w kecepatan sudut (angular), frekuensi sudut (angular) (w = 27if)

-Tanda asteriks dicantumkan pada nomor subbab untuk menandai bahwa subbab tersebut membahas suatu topik lanjut. Soal-soal yang sangat sulit, yang rumit pemecahannya, bisa saja ditandai dengan lebih dari satu tanda asteriks ini.

Huruf Yunani

A a Alpha N V Nu

B {3 Beta _� Xi

r r Gamma 0 0 Omicron

L1 8 Delta II 7r Pi

E € Epsilon p p Rho

z s Zeta L a Sigma

H _1} Eta T r Tau

e () Theta y V Upsilon

I Iota (/> _cp Phi

K K: Kappa X _X Chi

A A- Lambda _{IJ' If/} Psi

1

TARIK,

TEKAN,

DAN GESER

PENGANTAR MEKANI KA BAHAN

Mekanika bahan actalah cabang dari mekanika terapan yang membahas perilaku bencta pactat yang mengalami berbagai pembebanan. Nama-nama lain untuk bictang ilmu ini actalah kekuatan bahan ctan mekanika benda yang dapat berdeformasi. Bencta pactat yang ctitinjau ctalam buku ini meliputi batang (bars) ctengan beban aksial, poros (shafts) yang mengalami torsi, balok (beams) yang mengalami lentur, ctan kolom (columns) yang mengalami tekan.

Tujuan utama mekanika bahan actalah untuk menentukan tegangan

(stress), regangan (strain) ctan peralihan (displacement) pada struktur ctan komponen-komponennya akibat beban-beban yang bekerja pactanya. Apabila kita ctapat memperoleh besaran-besaran ini untuk semua harga beban hingga mencapai beban yang menyebabkan kegagalan, maka kita akan ctapat mempunyai gambaran lengkap mengenai perilaku mekanis pacta struktur tersebut. Pemahaman perilaku mekanis sangat penting untuk ctesain yang aman bagi semua jenis struktur, baik itu berupa pesawat terbang ctan antena, gectung ctan jembatan, mesin ctan motor, maupun kapal laut dan pesawat luar angkasa. ltulah sebabnya mekanika bahan actalah materi ctasar pacta begitu banyak cabang ilmu teknik. Statika ctan ctinamika juga penting, tetapi keduanya terutama membahas gaya ctan gerak yang berkaitan ctengan partikel ctan bencta tegar. Dalam mekanika bahan kita melangkah lebih jauh dengan mempelajari tegangan ctan regangan cti ctalam bencta nyata, yaitu bencta ctengan ctimensi terbatas yang bercteformasi akibat pembebanan. Untuk menentukan tegangan ctan regangan, kita menggunakan besaran-besaran fisik material selain juga berbagai aturan ctan konsep teoretis.

2 Bab 1 Tarik. Tekan. dan Geser

Riwayat perkembangan mekanika bahan merupakan kombinasi yang menarik antara teori dan eksperimen-teori telah menunj ukkan jalan ke hasil eksperimen yang berguna, begitu pula sebaliknya. Orang-orang terkenal seperti Leonardo da Yinci ( 1452 - 15 19) dan Galileo Galilei (1564 - 1642) telah melakukan eksperimen untuk menentukan kekuatan kawat, batang, dan balok, meskipun mereka tidak menge mbangkan teori yang me madai (berdasarkan standar masa kini) un tuk menjelaskan hasil penguj ian mereka. Sebaliknya, matematikawan temama Leonhard Euler (1707- 1 783) mengembangkan teori mate matis tentang kolom (column)

dan menghitung beban kritis sebuah kolom pada tahun 17-+4. jauh sebelum adanya bukti eksperimental untuk memperlihatkan signifikansi hasilnya. Tanpa adanya pengujian yang memadai untuk mendukung hasilnya, teori Euler sempat tidak digunakan selama lebih dari I 00 tahun. sekalipun saat ini teori tersebut merupakan dasar untuk desain dan analisis hampir semua kolom.·

Dalam mempelajari mekanika bahan, pembaca akan mendapatkan bahwa usaha yang dibutuhkan terbagi atas dua bagian. yaitu: pertama, memahami pengembangan logis konsep-konsepnya, dan kedua. menerap­ kan konsep-konsep tersebut ke dalam si tuasi praktis. Bagian pertama tercapai dengan mempelajari penurunan rumus, pembahasan dan contoh­ contoh yang ada di setiap bab sedangkan bagian kedua tercapai dengan memecahkan soal-soal di akhir setiap bab. Beberapa soal menggunakan angka (numerik) dan lainnya menggunakan simbol (aljabar).

Keuntungan dari soal numerik adalah bahwa semua besarannya terlihat jelas di setiap tahap perhitungan sehingga memberikan kesempatan untuk men ilai apakah harga n umerik tersebut masuk aka! atau tidak. Keuntungan utama dari soal simbolik adalah bahwa hasilnya berupa rumus yang serba guna. S uatu rumus menunj ukkan variabel-variabel yang mempengaruhi hasil akhir; sebagai contoh, kadang-kadang suatu besaran tidak muncul di dalam solusi, suatu fakta yang tidak terlihat jelas dalam solusi numerik. Selain itu, solusi aljabar menunj ukkan bagaimana masing-masing variabel mempengaruhi hasil, seperti ketika satu variabel muncul di pembilang dan variabel lain muncul di penyebut. Lebih jauh lagi, solusi simbolik memberikan kesempatan untuk mengecek dimensi pada setiap tahap perhitungan. Akhirnya, alasan paling penting untuk memecahkan secara aljabar adalah untuk mendapatkan rumus umu m yang dapat digunakan pada berbagai soal yang berbeda. Sebaliknya, solusi numerik hanya berlaku pada satu set kondisi. Karena seorang insinyur harus terbiasa dengan kedua jenis solusi tersebut, maka di dalam buku ini disajikan perpaduan antara soal numerik dan soal simbolik.

Soal-soal numerik mengharuskan pembaca bekerja dengan satuan pengukuran yang khusus. Agar sesuai dengan kondisi di dalam praktek, buku ini menggunakan Sistem Internasional (SI) dan Sistem U mum Amerika Serikat (USCS). Pembahasan mengenai kedua sistem ini diberikan dalam Lampiran A yang meliputi banyak tabel yang berguna termasuk tabel faktor konversi.

Semua soal terdapat di akhir setiap bab, dengan nomor soal yang menunj ukkan subbab asal soal-soal tersebut. Untuk soal-soal yang membutuhkan solusi numerik, soal yang bemomor ganjil mempunyai satuan USCS dan soal yang bernomor genap mempunyai satuan S I. Satu-satuny<,l

d;trl I -�

Gambar 1-1 _{Elemen struktur yang} mengalami beban aksial. (Batang penderek mengala mi tarik dan batang roda pendaratan mengalami tekiln.)

kekecualian adalah soal-soal yang melibatkan profil baja struktural yang umum diperdagangkan karena besaran dari profil ini ditabelkan dalam Lampiran E hanya dalam satuan USCS.

Teknik-teknik penyelesaian soal dibahas secara rinci dalam Lampiran

B. Selain memuat daftar prosedur rekayasa yang baik, Lampiran B juga memuat bagian-bagian tentang homogenitas dimensional dan angka penting. Topik-topik ini secara spesifik penting karena setiap persamaan harus homogen secara dimensional dan setiap hasil numerik harus dinyatakan dengan sejumlah angka penting yang tepat. Di dalam buku ini, hasil numerik akhir biasanya dinyatakan dengan tiga angka penting apabila suatu bilangan dimulai dengan angka 2 sampai 9, dan dengan empat angka penting apabila suatu bilangan dimulai dengan angka I. Harga-harga antara (intermediate value) biasanya dicatat dengan digit tambahan untuk meng­ hindari hilangnya ketelitian numeris akibat pembulatan bilangan.

TEGANGAN DAN REGANGAN NORMAL

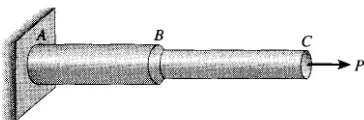
Konsep paling dasar dalam mekanika bahan adalah tegangan dan regangan. Konsep ini dapat diilustrasikan dalam bentuk yang paling men­ dasar dengan meninjau sebuah batang prismatis yang mengalami gaya aksial. Batang prismatis adalah sebuah elemen struktural lurus yang mem­ punyai penampang konstan di seluruh panjangnya, dan gaya aksial adalah beban yang mempunyai arah sama dengan sumbu elemen, sehingga meng­ akibatkan terjadinya tarik atau tekan pada batang. Contoh-contohnya diper­ lihatkan dalam Gambar 1 - 1 , di mana batang penderek tarik (tow bar) merupakan sebuah elemen prismatis yang mengalami tarik dan batang roda untuk pendaratan adalah elemen yang mengalami tekan. Contoh­ contoh lainnya adalah elemen di rangka batang pada jembatan, batang­ batang penghubung pada mesin mobil dan sepeda, kolom di gedung, dan flens tarik di pesawat terbang kecil.

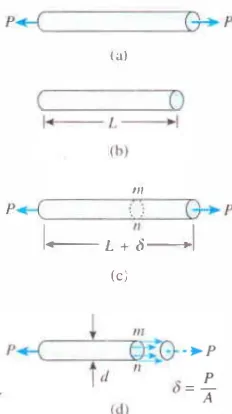
Untuk keperluan pembahasan, kita akan meninjau batang penderek dalam Gambar 1 - 1 dan mengisolasi salah satu segmennya sebagai benda bebas (Gambar 1-2a). Sewaktu menggambar diagram benda bebas ini, kita abaikan berat batang dan kita asumsikan bahwa gaya yang aktif hanyalah gaya aksial P di ujung-ujungnya. Selanjutnya kita tinjau dua kondisi batang tersebut, yang pertama sebelum beban diterapkan (Gambar l-2b) dan yang kedua sesudah beban diterapkan (Gambar 1-2c). Perhatikan bahwa panjang semula dari batang ditunjukkan dengan huruf L dan pertambahan panjangnya ditunjukkan dengan huruf Yunani 8 (delta).

Tegangan internal di batang akan terlihat apabila kita membuat sebuah potongan imajiner melalui batang pada bagian mn (Gambar l -2c). Karena

4 Bab 1 Tarik, Tekan, dan Geser yang mengalami tarik (a) diagram benda bebas dari segmen batang, (b) segmen batang sebelum di­ bebani, (c) segmen batang sesudah dibebani, dan (d) tegangan normal pada batang.

potongan ini diambil tegak lurus sumbu longitudinal batang, maka disebut

potongan melintang (penampang). Sekarang kita isolasi bagian dari batang di kiri potongan melintang mn sebagai benda bebas (Gambar l -2d). Di ujung kanan dari benda bebas ini (potongan mn) ditunjukkan aksi yang diberikan oleh bagian yang dihilangkan dari batang tersebut (yaitu bagian di kanan potongan mn) terhadap bagian sisanya. Aksi ini terdiri atas gaya terdistribusi kontinu yang bekerja pada seluruh penarnpang. Intensitas gaya (yaitu gaya per satuan luas) disebut tegangan dan diberi notasi huruf ¥unani a (sigma). Jadi, gaya aksial P yang bekerja di penampang adalah resultan dari tegangan y ang terdistribusi kontinu . (Gaya resultan ditunjukkan dengan garis putus-putus di dalam Gambar l -2d.)

Dengan mengasumsikan bahwa tegangan terbagi rata di seluruh potongan mn (Gambar l-2d), kita dapat melihat bahwa resultannya hams sama dengan intensitas a dikalikan dengan luas penampang A dari batang tersebut. Dengan demikian, kita mendapatkan rumus berikut untuk menyatakan besar tegangan:

p

A (1-1)

Persamaan ini memberikan intensitas tegangan merata pada batang prismatis yang dibebani secara aksial dengan penampang sembarang. Apabila batang ini ditarik dengan gaya P, maka tegangannya adalah

tegangan tarik (tensile stress); apabila gayanya mempunyai arah sebaliknya, sehingga menyebabkan batang tersebut mengalami tekan, maka terj adi tegangan tekan (compressive stress). Karena tegangan ini mempunyai arah yang tegak lurus permukaan potongan, maka tegangan ini disebut tcgangan normal (normal stress). Jadi, tegangan normal dapat berupa tarik atau tekan. Selanjutnya, di dalam Subbab 1.6, kita akan menjumpai jenis tegangan lainnya, yang disebut tegangan geser, yang bekerja sejajar terhadap permukaan potongan.

Apabila konvensi tanda untuk tegangan normal dibutuhkan, biasanya tegangan tarik didefinisikan bertanda positif dan tegangan tekan bertanda negatif.

Karena tegangan normal a diperoleh dengan membagi gaya aksial dengan luas penampang, maka satuannya adalah gaya per satuan luas. Jika satuan uses digunakan, maka tegangan biasanya dinyatakan dalam pound per inci kuadrat (psi) atau kip per inci kuadrat (ksi).' Sebagai contoh, misalkan batang dalam Gambar 1 -2 mempunyai diameter d sebesar 2,0 in. dan beban P mempunyai besar 6 kips. Dengan demikian, tegangan di batang adalah

Apabila satuan SI digunakan, gaya dinyatakan dalam newton (N) dan luas dalam meter kuadrat (m2). Dengan demikian, tegangan mempunyai satuan newton per meter kuadrat (N/m2), yang disebut juga pascal (Pa). Tetapi, pascal adalah satuan yang sedernikian kecilnya sehingga dibutuhkan pengali yang besar, maka biasanya digunakan megapascal (MPa). Untuk

.

G amba r 1 -3 _{B a tang pendel}

dari baja yang mengalami beban tarik, P.

mengilustrasikan bahwa satu pascal memang kecil, kita hanya perlu mengingat bahwa 1 psi kira-kira sama dengan 7000 pascal. Sebagai contoh numerik, tegangan yang dibahas dalam paragraf sebelum ini ( 1 ,9 1 ksi) ekivalen dengan 13,2 MPa yang sama dengan 1 3,2 x 106 pascal. Meskipun tidak diharuskan dalam SI, pembaca kadang-kadang menjumpai tegangan dinyatakan dalam satuan newton per milimeter kuadrat (N/mm2), yang sama dengan MPa.

Persamaan cr =PIA hanya berlaku jika tegangan terbagi rata di seluruh penampang batang. Kondisi ini terjadi jika gaya aksial P bekerja melalui pusat berat penampang, sebagaimana ditunjukkan di bagian lain dari subbab ini. Apabila beban P tidak bekerja di pusat berat, maka lentur batang akan terjadi, dan analisis yang lebih rumit dibutuhkan (lihat Subbab 5 . 1 2 dan 1 1 .5). Namun, di dalam buku ini (sebagaimana juga dijumpai di dalam praktek) dianggap bahwa gaya aksial diterapkan di pusat berat penampang, kecuali apabila dinyatakan tidak demikian.

Kondisi tegangan merata yang ditunjukkan dalam Gambar l -2d terjadi di seluruh panjang batang kecuali di dekat ujung-ujungnya. Distribusi tegangan di ujung batang bergantung pada bagaimana beban P disalurkan ke batang, Jika beban tersebut terbagi rata di ujungnya, maka pola tegangan di ujung akan sama dengan di seluruh bagian lainnya. Sekalipun demikian, beban sangat mungkin disalurkan melalui sendi atau baut, yang menyebab­ kan terjadinya tegangan yang sangat terlokalisasi yang disebut konsentrasi tegangan. Salah satu kemungk:inannya adalah dengan menggunakan batang pendel seperti terlihat dalam Gambar 1 -3. Dalam hal ini beban P disalurkan ke batang tersebut melalui sendi yang melalui lubang (atau mata) di ujung­ uj ung batang. Jadi, gaya-gaya di dalam gambar tersebut sebenarnya merupakan resultan dari tekanan tumpu antara sendi dan batang pendel, dan distribusi tegangan di sekitar 1ubang cukup rumit. Sekalipun demik:ian, apabila kita bergerak menjauhi ujung ke arah tengah batang, distribusi tegangan akan secara gradual mendekati distribusi yang rata sebagaimana terlihat dalam Gambar l -2d.

Sebagai petunjuk praktis, rumus cr = PIA dapat digunakan dengan ketelitian yang baik untuk sembarang titik di dalam batang prismatis, yaitu setidaknya sejauh mungk:in dari konsentrasi tegangan sebagai dimensi lateral terbesar dari batang tersebut. Dengan perkataan lain, distribusi tegangan di dalam Gambar 1-2d terbagi rata pada jarak d atau lebih besar dari ujung-ujungnya, dimana d adalah diameter batang dan distribusi tegangan di batang pendel (Gambar 1 -3) terbagi rata pada jarak b atau lebih besar dari ujung yang diperbesar, dengan b adalah lebar batang. Pembahasan yang lebih rinci tentang konsentrasi tegangan yang diakibatkan oleh beban aksial diberikan dalam Subbab 2. 1 0.

Tentu saja, meskipun tegangan tidak terbagi rata, persamaan _{cr =PIA} masih tetap berguna karena persamaan ini memberikan tegangan normal rata-rata di suatu penampang.

• Regangan Normal

6 Bab 1 Tarik, Tekan, dan Geser

sama di mana pun di dalam batang. Selanjutnya, jika kita meninjau setengah bagian dari batang (panjangnya L/2), bagian ini akan mempunyai perpanjangan yang sama dengan

/5/

2, dan jika kita meninjau seperempat bagian dari batang, bagian ini akan mempunyai perpanjangan yang sama dengan

/5/4.

Dengan cara yang sama, satu satuan panjang dari batang tersebut akan mempunyai perpanjangan yang sama dengan 1/L kali perpanjangan total 8. Dengan proses ini kita akan sampai pada konsep perpanjangan per satuan panjang, atau rcgangan, yang diberi notasi huruf

Yunani e (epsilon) dan dihitung dengan persamaan

e = o

L (1 -2)

Jika batang tersebut mengalami tarik, maka regangannya disebut rcgangan

tarik, yang menunjukkan perpanjangan bahan. Jika batang tersebut meng­

alami tekan, maka regangannya adalah regangan tckan dan batang tersebut memendek. Regangan tarik biasanya bertanda positif dan regangan tekan bertanda negatif. Regangan e disebut regangan normal karena regangan ini berkaitan dengan tegangan normal.

Karena merupakan rasio antara dua panjang, maka regangan normal ini merupakan hcsaran tak herdimensi, artinya regangan tidak mempunyai satuan. Dengan demikian, regangan dinyatakan hanya dengan suatu bilangan, tidak bergantung pada sistem satuan apapun. Harga numerik dari regangan biasanya sangat kecil karena batang yang terbuat dari bahan struktural hanya mengalami perubahan panjang yang kecil apabila dibebani. Sebagai contoh, tinjau batang baja yang mempunyai panjang L sama dengan 2,0 m. Apabila dibebani tarik yang cukup besar, batang tersebut dapat memanjang sebesar 1,4 mm, yang berarti regangannya

e = §_ =

1•4

mm = 0,0007 = 700 x 10--{)

L 2,0 m

Dalam praktek, satuan _o dan L kadang-kadang disertakan dalam regangan, dan regangan ditulis dalam bentuk seperti mm/m, .urnlm, dan in./in. Sebagai contoh, regangan e pacta ilustrasi di atas dapat ditulis dengan 700 .urnlm atau 700 x 10� in./in. Kadang-kadang regangan juga dinyatakan dalam persen, khususnya jika regangan tersebut besar. (Di dalam contoh di atas, regangan adalah 0,07%.)

• Regangan dan Tegangan Uniaksial

Definisi tegangan normal dan regangan normal semata-mata didasarkan atas tinjauan statika dan geometris saja, yang berarti bahwa persamaan (I­

I) dan (1-2) dapat digunakan untuk berbagai beban besar berapapun dan

berbagai jenis material (bahan). Persyaratan utama adalah bahwa deformasi batang adalah sama di seluruh volumenya, yang pada gilirannya mengharuskan batang tersebut prismatis, beban bekerja melalui pusat berat

penampang dan bahannya homogen (yaitu, sama di seluruh bagian dari

batang tersebut). Keadaan tegangan dan regangan yang dihasilkan disebut

tegangan uniaksial dan regangan. Pembahasan lebih lanjut tentang

tegangan uniaksial, termasuk juga tegangan dan regangan pada batang

yang bukan longitudinal, diberikan dalam subbab 2.6. Kita juga akan

(,1)

(bi

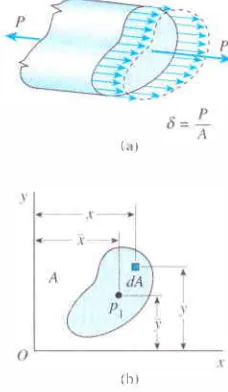
Gambar 1 -4 _{Distribusi tegangan} tcrbagi rata di suatu batang prismatis : (a) gaya aksial P, dan (b) penampang melintang batang

• Garis Kerja Gaya Aksial untuk Distribusi Tegangan Terbagi Rata Di seluruh pembahasan terdahulu tentang tegangan dan regangan di batang prismatis, kita asumsikan bahwa tegangan normal CJ mempunyai distribusi terbagi rata di seluruh penampang. Sekarang kita akan menunjukkan bahwa kondisi ini terpenuhi jika garis kerja gaya aksial melalui pusat berat penampang melintang.

Tinjaulah batang prismatis yang mempunyai bentuk penampang sembarang yang mengalami gaya aksial P yang menyebabkan terjadinya tegangan terbagi rata (Gambar l -4a). Juga, misalkan _p1 adalah titik pada

CJ penampang di mana garis kerja gaya memotong penampang (Gambar l -4b ). Kita buat si stem sumbu xy pada bidang pen am pang dan ea tat koordinat titik _p1 dengan x dan y. Untuk menentukan koordinat ini, kita amati bahwa momen M, dan M, dari gaya P masing-masing terhadap sumbu x dan y, harus sama dengan momen yang berkaitan dengan tegangan terbagi rata.

Momen dari gaya P adalah

(a, b)

di mana momen dipandang positif apabila vektomya ( dengan menggunakan aturan tangan kanan) bekerja dalam arah positif sumbunya.*

Momen dari tegangan yang terdistribusi diperoleh dengan meng­

integrasikannya di seluruh penampang A. Gaya diferensial yang bekerja

pada suatu elemen luas dA (Gambar l -4b) sama dengan CJdA. Momen dari

gaya tersebut terhadap sumbu x dan y adalah masing-masing aydA dan -CJXdA, yang mana x dan y menunjukkan koordinat elemen dA. Momen total diperoleh dengan mengitegrasikannya terhadap luas penampang; jadi, kita peroleh

(c,d)

Pemyataan ini memberikan momen yang dihasilkan oleh tegangan CJ.

Selanjutnya, kita samakan momen M, dan M, yang diperoleh dari

gay a P (Persamaan a dan b) dengan m omen yang diperoleh dari tegangan

yang terdistribusi (Persamaan c dan d):

Py=

I

ay dA Px =

-Im

dA

Karena tegangan CJ terbagi rata, maka kita ketahui bahwa nilainya konstan

di seluruh penampang A dan dapat diletakkan di luar tanda integrasi. Juga,

kita ketahui bahwa tegangan sama dengan PIA. Dengan demikian, kita

peroleh rumus berikut untuk koordinat titik _p;:

-

0)' dA

\' = X =

I

0)' dA ( 1 -3a,b)

A A

Persamaan ini sama dengan persamaan yang mendefinisikan koordinat pusat berat suatu area (lihat Pers. 12-3a dan b). Dengan demikian, kita

sekarang telah sampai pada sebuah kesimpulan penting. Untuk memperoleh

tarik atau tekan yang terbagi rata pada suatu batang prismatis, gaya

B Bab 1 Tarik, Tekan, dan Geser

aksial harus bekerja melalui pusat berat penampang. Sebagaimana telah diuraikan sebelum ini, kita selalu mengasumsikan bahwa kondisi ini terpenuhi, kecuali jika secara eksplisit dinyatakan tidak demikian.

Contoh berikut ini mengilustrasikan perhitungan tegangan dan regangan pada batang prismatis. Dalam contoh pertama, kita mengabaikan berat batang dan dalam contoh kedua kita memasukkannya. (Agar sesuai dengan buku-buku praktek pada umumnya, kita selalu mengabaikan berat suatu struktur apabila memecahkan suatu soal, kecuali apabila diinstruksi­ kan untuk memasukkannya.)

• Contoh 1-1

5- H

Gambar _{1 -5} Contoh 1 - 1 . Tiang aluminium berlubang yang meng­ alami tekan

Sebuah tiang pendek berupa tabung 1ingkaran berlubang dari aluminium memikul beban tekan sebesar 54 kips (Gambar 1 -5). Diameter dalam dan luar dari tabung tersebut masing-masing adalah

d1

= 3,6 in dan

d2

= 5,0 in. dan panjangnya adalah 40 in. Perpendekan tiang akibat beban tersebut diukur sebesar 0,022 in. Tentukanlah tegangan dan regangan tekan di tiang tersebut. (Abaikan berat tiang itu sendiri dan asumsikan bahwa tiang tersebut tidak menekuk akibat beban tersebut.)

Solusi

Asumsikan bahwa beban tekan bekerja di pusat tabung berlubang sehingga kita dapat menggunakan persamaan s = PIA (Pers. 1 - 1 ) untuk menghitung tegangan normal. Gaya

P

sama dengan 54 k (atau 54000 lb), dan luas penampang melintang A adalah

A =

%(

dff - d�)

=

%[

(5,0 in.)2 -(3,6 in.)2

]

Dengan demikian, tegangan tekan di tiang ada1ah

a = !!_ = 54.000 lb = 5710 psi

A 9,456 in.2

Regangan tekan (dari Persamaan 1 -2) adalah

E = §_ = 0·02-in. = 550 X 10-6

L 40 m.2

-Jadi, tegangan dan regangan di tiang telah dihitung.

9,456 in.2

-Catatan: Sebagaimana telah diterangkan sebelum ini, regangan merupakan besaran yang tak berdimensi dan tidak ada satuan yang dibutuhkan. Namun untuk kejelasan, satuan juga sering digunakan. Dalam contoh ini, E dapat saja ditulis

sebesar 550 X I 0"6 in./in. atau 550 ,uin./in.

• Contoh 1-2

Suatu batang baja berpenampang lingkaran yang panjangnya L dan berdiameter

d

dibebani W di ujung hawnhnya ( amhru 1 -6). (a) Dapatkan rumu lmtuk tegangan maksimum _amak> di batang tcr ·ebut dengan rnemperh it ungkan b 'r.ll �cndiri batang tersebut. (b) Hitunglah tegangan maksimum j tkn L = 40 1 0 , t1 = mm, dan W =

d -..

-Gambar 1-6 _{Contoh l -2. Batang}

bulat dari baja yang memikul beban

w.

Solusi

(a) Gaya aksial maksimum F'""*' di batang terjadi di ujung alas dan sama dengan

berat W ditambah berat W0 dari batang itu sendiri. Berat sendiri batang sama

dengan berat jenis y baja dikalikan volume batang V, atau

% = y\1 = yAL ( l-4) dengan A adalah luas penampang batang. Dengan demikian, rumus untuk tegangan maksimum (dari Persamaan 1 - 1 ) menjadi

a = Fmaks = W + yAL = W +

maks _{A A A} ( 1 -5 ) ..

(b) Untuk menghitung tegangan maksimum, k.ita masukkan harga-harga numerik ke dalam persamaan di atas. Luas penampang melintang sama dengan ruP/4, dengan d = 8 mm, dan beratjenis baja y= 77,0 k.N/m3 (dari Tabel H- 1 di Lampiran H). Jadi

1 •5 kN _{+ (77,0 k.N/m3)(40 m)} n-(8 mm)2 /4

= 29,84 MPa + 3. 1 I MPa = 33,0 MPa _.. Di dalam contoh ini, berat batang berkontribusi secara signifikan terhadap tegangan maksimum dan sebaiknya tidak diabaikan.

BESARAN MEKANIS BAHAN

Untuk mendesain mesin dan struktur agar keduanya berfungsi secara me­ madai kita harus memahami perilaku mekanis dari material (bahan) yang digunakan. Biasanya, satu-satunya cara untuk menentukan bagaimana suatu bahan berperilaku apabila mengalami pembebanan adalah dengan melakukan eksperimen di laboratorium. Prosedur yang biasa a�alah dengan meletakkan benda uji kecil dari material tersebut pacta mesin penguji, menerapkan beban, dan selanjutnya mengukur deformasinya (seperti misalnya perubahan panjang dan perubahan diameter). Hampir semua laboratorium pengujian bahan diperlengkapi dengan mesin-mesin yang mampu membebani benda uji dengan berbagai cara, termasuk pembebanan statik dan dinamik, baik tarik maupun tekan.

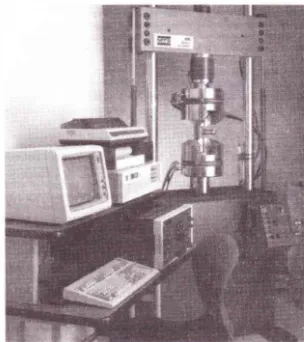
Mcsin uji tarik tipikal ditunjukkan dalam Gambar 1-7. Benda uji dipasang di antara kedua penjepit besar dari mesin uji dan selanjutnya dibebani tarik. Alat pengukur akan mencatat deformasi, sementara sistem kontrol otomatis serta pengolah data (di kiri foto) membuat tabel dan grafik dari hasil pengujian.

1 0 Bab 1 Tarik, Tekan, dan Geser

G a m bar 1 ·7 _{Mesin uji tarik} dengan s i s tem pengolahan data (Atas izin MTS System Corpora­ tion)

hanya mengalami tarik murni. Situasi ini ditunj ukkan dalam Gambar 1 -8, di mana benda uji baja baru saja terputus akibat dibebani. Alat di kiri, yang dihubungkan oleh dua buah lengan ke benda uji, adalah extensom­

cter untuk mengukur perpanjangan selama pembebanan.

Agar hasil pengujian dapat dibandingkan, maka dimensi benda uji dan metode penerapan beban telah distandarisasi. Organisasi pembuat standar yang paling utama adalah American Society for Testing and Ma­ terials (ASTM), suatu badan teknis nasional yang menerbitkan spesifikasi dan standar untuk bahan dan pengujian. Organisasi lain yang sejenis di Amerika Serikat adalah American Standards Association (ASA), dan

National Institute of Standards and Institute (NIST), yang sebelumnya bernama National Bureau of Standards (NBS). Organisasi serupa ada di negara-negara lain.

Gambar 1 -8 B enda uji tarik tipikal dengan extensometer yang terpasang padanya; benda uji baru saja terputus karena tarik (Atas izin MTS System Corporation)

Pnnjang terukur

uji. Tetapi, dalam uji dinamis beban diterapkan secara cepat dan kadang­ kadang dengan cara siklus. Karena sifat beban dinamis mempengaruhi besaran bahan, maka laju pembebanan perlu juga dicatat.

llji tekan pada metal biasanya dilakukan pacta benda uji kecil yang berbentuk kubus atau silinder. Kubus biasanya mempunyai sisi 2,0 in. dan silinder biasanya mempunyai diameter sekitar 1 in. dan panjangnya I sampai 1 2 in. Besarnya beban yang diterapkan dan besarnya perpendekan benda uji dapat diukur. Perpendekan sebaiknya diukur di seluruh panjang terukur yang kurang dari panjang total dari benda uji agar tidak ada efek ujung.

Beton diuji tekan pada setiap proyek konstruksi yang penting untuk menjamin bahwa kekuatan yang dibutuhkan telah dicapai. Benda uji menurut standar ASTM mempunyai diameter 6 in dan panjang 1 2 in,

serta mempunyai umur 28 hari (umur beton merupakan ha! yang penting karena beton meningkat kekuatannya apabila mengering). Benda uji serupa yang agak lebih kecil digunakan dalam melakukan uji tekan pada batuan (Gambar 1 -9).

• Diagram Tegangan-Regangan

1 2 Bab 1 Tarik, Tekan, dan Geser

Gambar _{1 -9 Benda uji batuan} yang diuji tekan. (Atas izin MTS System Corporation)

hasil pengujian dalam bentuk yang dapat diterapkan pada elemen struktur yang berukuran berapapun. Cara sederhana untuk mencapai tujuan ini adalah dengan mengkonversikan hasil pengujian tersebut ke tegangan dan regangan.

Tegangan aksial er pada benda uji dihitung dengan membagi beban

aksial P dengan luas pen am pang A (lihat Persamaan l - 1 ). Jika luas awal benda uji digunakan dalam perhitungan, maka tegangan yang diperoleh

disebut tcgangan nominal (nama lainnya adalah tegangan konvensional

dan tegangan teknik). Harga tegangan aksial yang lebih eksak, yang disehut

tcga ngan scbenarn� a, dapat dihitung dengan menggunakan luas penam­ pang batang sebenarnya pada saat kegagalan terjadi. Karena l uas aktual dalam pengujian tarik selalu lebih kecil daripada luas awal (sebagaimana diilustrasikan dalam Gambar 1 -8), maka tegangan sebenarnya selalu lebih besar daripada tegangan nominal.

Regangan aksial rata-rata £ pada benda uji diperoleh dengan membagi

perpanjangan yang diukur 8 antara tanda-tanda pengukuran dengan panjang

terukur L (lihat Gambar 1 -8 dan Persamaan J -2). Jika panjang terukur

awal digunakan dalam perhitungan (misalnya 2,0 in.), maka didapatkan

Gambar _{1 - 1 0 Diagram tegangan­} regangan untuk baja struktural tipikal yang mengalami tarik (tidak berskala)

sebenarnya (atau regangan a/ami) pacta setiap harga beban dengan menggunakan jarak aktual antara tanda-tanda pengukuran. Dalam keadaan larik, regangan sebenarnya selalu lebih kecil daripada regangan normal. Sekalipun demikian, untuk penggunaan dalam bidang teknik, tegangan nominal dan regangan nominal sudah cukup memadai, sebagaimana akan diuraikan dalarn bagian lain subbab ini.

Sesudah melakukan uji tarik atau tekan dan menentukan tegangan dan regangan pacta berbagai taraf beban, kita dapat memplot diagram tegangan versus regangan. Diagram tegangan-regangan seperti ini merupakan karakteristik dari bahan yang diuji dan memberikan informasi penting tentang besaran mekanis dan jenis perilaku.*

Bahan pertama yang akan kita bahas adalah baja struktural, yang

juga dikenal dengari baja lunak atau baja karbon rendah. Baja struktural

adalah salah satu bahan metal yang paling banyak digunakan untuk gedung,

jembatan, crane, kapal, menara, kendaraan, dan berbagai jenis struktur

lain. Diagram tegangan-regangan untuk baja struktural tipikal yang

mengalami tarik ditunjukkan dalam Gambar 1 - 1 0. Regangan diplot pada

sumbu horizontal dan tegangan pacta sumbu vertikal. (Untuk menunjukkan

semua hal penting dari bahan ini, sumbu regangan dalam Gambar 1 - 1 0

digambar tanpa skala.)

Diagram tersebut dimulai dengan garis lurus dari pusat sumbu 0 ke titik A, yang berarti bahwa hubungan antara tega.ngan dan regangan pacta daerah awal ini bukan saja linier melainkan juga proporsional. •• Melewati titik A, proporsionalitas antara tegangan dan regangan tidak acta lagi; jadi tegangan di A disebut limH Untuk baja berkarbon rendah, limit ini berada pacta selang 30 sampai 50 ksi (2 1 0 sampai 350 MPa), tetapi baja berkekuatan tinggi (dengan kandungan karbon lebih tinggi ditambah unsur paduan lain) dapat mempunyai batas proporsional lebih dari 80 ksi (550 MPa). Kemiringan garis lurus dari 0 ke A disebut modu­ lus clastisitas. Karena kemiringan mempunyai satuan tegangan dibagi

Tegangan

ultiHoatc ..

Tegangan

luluh ---..

Limit / proporsional

Daerah linier

Luluh atau Strain plastisitas hardening

sempurna

£'

-- ·

Necking

·I )iagt dill lc�<lll�:ln-r cg<tllt!-<111 di 1 i Ill i-; olcll J:1C11h Hl'rlll Ju l l r ( 1 6.'1--i-· I 70.� ) dan I V Polll'l'k·l ( 1

7�X-1 Kh 7 7�X-1 : l i hlll 1{,· 1 1 --1;

J )ud \ <l l l ; ilk·i Li i"l'l"'ll l /JI O,'JOI \111111.'1 j l l, a r ;J>.;ru <l!lld l ;l h-l'li l l < l l l ) a h:on-.;lt�ll l kn:;a11 t k� m r kltill, '>Ualu l\uh1111_::.111 j)l l lf'( )J , inn:d dar1;1{ clinv<�tak;rn tk'H.�dll "i�o.'hl l;tll �.tl i ' 1 u 1 u" ! '-lll.!,.' lll�ltl l u 1 pll.'<llll)'il \!;Jillllll huhuH.C<�Il p1 0j)l l! .., l llll�ll l HI�l� �ann LiL'Il!;i.lll l tu h l l l l�illl /i11in \k-..kiJ'Uil h u hun�an p1 1 1)10I "ion;tl ;ublall

l i ltll'l ...,L·h�i l i � n : a L1Ja� -..LI<liu he nil I k.IJL'Il;t ..;u;tl\1 JH,hungan ) �Ill� dilly;tl<tk;_ln dLJJ!:,!-�l l l ga1 1" l u J u " y;tn� 1 1d<1�

1 4 Bab 1 Tarik, Tekan, dan Geser batang baja lunak yang mengalami tarik

regangan, maka modulus elastisitas mempunyai satuan yang sama dengan tegangan. (Modulus elastisitas dibahas lebih lanjut di Subbab 1 .5 .)

Dengan meningkatnya tegangan hingga melewati limit proporsional, maka regangan mulai meningkat secara lebih cepat lagi untuk setiap per­ tambahan tegangan . Dengan demikian, kurva tegangan-regangan mempunyai kemiringan yang berangsur-angsur semakin kecil, sampai pada titik B kurva tersebut menjadi horizontal (lihat Gambar 1 - 1 0). Mulai dari titik ini, terjadi perpanjangan yang cukup besar pada benda uji tanpa adanya pertambahan gaya tarik (dari B ke C). Fenomena ini disebut luluh dari bahan, dan titik B disebut litik luluh. Tegangan yang berkaitan dengan ini disebut tega ngan luluh dari baja. Di daerah antara B dan C, bahan ini menjadi plastis semJmrn a, yang berarti bahwa bahan ini berdeformasi tanpa adanya pertambahan beban. Perpanjangan benda uji baja lunak pada daerah plastis sempuma pada umumnya 1 0 sampai 1 5 kali perpanjangan yang terjadi di daerah linier (antara awalnya pembebanan dan limit proporsional). Adanya regangan yang sangat besar di daerah plastis (dan setelah itu) adalah alasan mengapa diagram tersebut diplot tidak berskala.

Sesudah mengalami regangan besar yang terjadi selama peluluhan di daerah BC, baja mulai mengalami pengerasan regang ( stra i n hardening/.

Selama itu, bahan mengalami perubahan dalam struktur kristalin, yang menghasilkan peningkatan resistensi bahan tersebut terhadap deformasi lebih lanjut. Perpanjangan benda uj i di daerah ini membutuhkan peningkatan beban tarik, sehingga diagram tegangan-regangan mempunyai kemiringan positif dari C ke D. Beban tersebut pada akhimya mencapai harga maksimumnya, dan tegangan pada saat itu (di titik D) disebut tegangan ultimate. Penarikan batang lebih lanjut pada kenyataannya akan disertai dengan pengurangan beban dan akhimya terjadi putus/patah di suatu titik seperti titik E pada Gambar 1 - 1 0.

Tegangan luluh dan tegangan ultimate dari suatu bahan disebut juga masing-masing kekuatan luluh dan kekuatan ultimatl' h.l'lmatan adalah sebutan umum yang merujuk pada kapasitas suatu struktur untuk menahan beban. Sebagai contoh, kekuatan luluh dari suatu balok adalah besarnya beban yang dibutuhkan untuk terjadinya luluh di balok tersebut, dan kekuatan ultimate dari suatu rangka batang adalah beban maksimum yang dapat dipikulnya, yaitu beban gagal. Tetapi, dalam melakukan uji tarik untuk suatu bahan, kita definisikan kapasitas pikul beban dengan tegangan di suatu benda uji, bukannya beban total yang bekerja pada benda uji. Karena itu, kekuatan bahan biasanya dinyatakan dalam tegangan.

Apabila suatu benda uji ditarik, terjadi juga kon t rak.si lateral, sebagaimana telah disebutkan sebelum ini. Pengurangan luas penampang yang ditimbulkannya cukup kecil terhadap perhitungan tegangan hingga sekitar titik C dalam Gambar 1 - 10, tetapi melewati titik tersebut, pengurangan luas mulai mengubah bentuk kurva. Di sekitar tegangan ultimate, pengurangan luas menjadi sangat nyata dan neck in�; (pembentuk­ an leher) pada batang tersebut terjadi (lihat Gambar 1-8 dan 1 - 1 1 ). Jika luas aktual penampang di bagian yang mengecil dari leher ini digunakan untuk menghitung tegangan, maka kurva lq�angan-regan�an sehena rn.' a (garis putus CE · dalam Gambar 1 - 10) akan diperoleh. Be ban total yang

rr (ksi) tipikal yang mengalami tarik (digambar berskala)

Gambar 1 -1 3Diagram tegangan­ ' egangan untuk senyawa aluminium

tegangan sebenamya hingga terjadi kegagalan (titik E'). Karena hampir semua struktur diharapkan berfungsi pada tegangan di bawah limit proporsional, maka k urva tegangan-regangan konvcnsional OABCDE, yang didasarkan atas luas penampang awal benda uji dan yang mudah untuk dihitung, memberikan informasi yang cukup baik untuk digunakan dalam desain teknik.

Diagram dalam Gambar 1 - 1 0 menunjukkan karakteristik umum dari kurva tegangan-regangan untuk baja 1unak, tetapi proporsinya tidak realistis karena, sebagaimana telah disebutkan, regangan yang terjadi dari B ke C mungkin lebih daripada sepuluh kali regangan yang terjadi dari 0 ke A. Se1ain itu, regangan dari C ke E beberapa kali lebih besar daripada dari B ke C. Hubungan yang benar ditunjukkan da1am Gambar 1 - 1 2, yang menunjukkan diagram tegangan-regangan untuk baja lunak yang digambar berskala. Di dalam gambar ini, regangan dari titik no! ke titik A sedemikian kecilnya dibandingkan dengan regangan dari titik A ke titik E sehingga regangan tersebut tidak terlihat, dan bagian awal dari diagram ini nampak seperti garis vertikal.

Adanya titik lu1uh yang je1as yang diikuti dengan regangan plastis merupakan karakteristik penting dari baja struktural yang kadang-kadang digunakan dalam desain (lihat, sebagai contoh, pembahasan perilaku elastoplastis dalam Subbab 2. 1 2, 3. 12, dan 6.9). Metal seperti baja struktural yang mengalami regangan permanen besar sebelum kegagalan terjadi di­ kelompokkan ke dalam bahan yang daktil (ulct). Sebagai contoh, daktilitas (keuletan) adalah sifat yang memungkinkan suatu batang baja untuk dibeng­ kokkan membentuk busur lingkaran tanpa putus atau ditarik menjadi kawat tanpa mengalami kerusakan. Keunggulan yang diharapkan dari bahan yang daktil adalah bahwa distorsi nyata dapat terjadi jika beban menjadi terlalu besar, sehingga memberikan kesempatan untuk melakukan sesuatu sebelum patah (fraktur) aktual terjadi. Selain itu, bahan yang berperilaku daktil mampu menyerap sejumlah besar energi regangan sebelum mengalami fraktur.

Baja struktural adalah paduan besi yang mengandung sekitar 0,2% karbon, sehingga disebut dengan baja karbon rendah. Dengan bertambahnya kadar karbon, baja menjadi kurang daktil tetapi menj adi lebih kuat (mempunyai tegangan luluh dan tegangan ultimate lebih tinggi). Besaran fisik bajajuga dipengaruhi oleh perlakuan panas yang dialaminya, adanya metal lain, dan proses pembuatan seperti pengerokan. Material lain yang berperilaku secara daktil (pada kondisi tertentu) meliputi aluminium, tembaga, magnesium, timbal, molybdenum, nikel, perunggu, brons monel metal, nilon, dan teflon.

Meskipun bahan-bahan tersebut mempunyai daktilitas yang cukup besar, paduan aluminium pada umumnya tidak mempunyai titik luluh yang jelas, sebagaimana ditunjukkan dalam kurva tegangan-regangan dalam Gambar 1 - 1 3 . Sekalipun demikian, bahan ini mempunyai daerah linier awal dengan limit proporsional yang terlihat jelas. Paduan yang diproduksi untuk maksud struktural mempunyai limit proporsional dalam selang 1 0 sampai 60 ksi (70 sampai 410 MPa) dan tegangan ultimate dalam selang 20 sampai 80 ksi ( 1 40 sampai 550 MPa).

16 Bab 1 Tarik, Tekan, dan Geser regangan untuk dua jenis karet yang mengalami tarik

E

Gambar 1 -1 6 Diagram tegangan­ regangan tipikal untuk bahan getas yang menunjukkan limit propor­ sional (titik A) dan tegangan fraktur (titik B)

dengan bagian linier awal dari kurva tersebut (Gambar 1 - 14) tetapi mempunyai offset regangan standar tertentu, misalnya 0,002 (atau 0,2%). Perpotongan garis offset dan kurva tegangan-regangan (titik A dalam gambar ini) didefinisikan sebagai tegangan luluh. Karena tegangan ini ditentukan dengan aturan yang opsional dan bukan merupakan besaran fisik bahan sebenamya, maka ha! ini harus dibedakan dengan tegangan luluh sebenamya dengan cara menyebutnya lega ngan l u l u h l�f.l\et. Untuk bahan seperti aluminium, tegangan luluh offset terletak sedikit di atas limit proporsional. Dalam ha! baja struktural, dengan adanya transisi mendadak dari daerah linier ke daerah plastis, tegangan offset pada dasamya sama dengan tegangan luluh dan limit proporsional.

Karet mempunyai hubungan linier antara tegangan dan regangan

sampai regangan yang relatif besar (dibandingkan dengan metal). Regangan pada limit proporsional dapat sebesar 0, 1 atau 0,2 ( 10% atau 209c )_. Setelah limit proporsional, perilakunya bergantung pada jenis karet (Gambar 1

-1 5). Beberapa jenis karet akan inemanjang sangat besar tanpa mengalami kegagalan, hingga panjangnya dapat mencapai beberapa kali panjang semula. Bahan tersebut pada dasamya mempunyai tahanan yang meningkat jika dibebani, dan kurva tegangan-regangannya jelas berarah ke atas. Pembaca dapat dengan mudah mengamati perilaku seperti ini dengan menarik karet gelang dengan tangan. (Perhatikan bahwa meskipun karet dapat mengalami regangan sangat besar, bahan ini bukanlah bahan daktil karena regangannya tidak permanen.)

Daktilitas bahan yang mengalami tarik dapat dilihat dengan mengamati perpanjangan bahan dan reduksi luas pada penampang di mana fraktur terjadi. Pcrscntase pcrpanjanga n didefini sikan sebagai

Lr - Le>

Persentase perpanjangan = · Lo (1 00) ( 1 -6)

dengan _L0 adalah panjang terukur awal dan _Lr adalah jarak antara tanda­ tanda pengukuran pada saat fraktur. Karena perpanjangan tidak sama di seluruh panjang benda uji tetapi terpusat di daerah di mana terjadi neck­ ing, maka persentase perpanjangan bergantung pada panjang terukur. Dengan demikian, dalam menyatakan persentase perpanjangan, panjang terukur harus diketahui. Untuk panjang terukur 2 in, baja dapat mempunyai perpanjangan dalam selang 3% sampai 40%, bergantung pada komposisi; dalam ha! baja struktural, dengan harga yang umum adalah 20% atau

30%. Perpanjangan paduan aluminium bervariasi dari 1 % sampai 45%,

bergantung pada komposisi dan perawatannya.

Pcrsentasc red u ksi l uas menunjukkan besamya necking yang terjadi dan

didefinisikan sebagai

�l ·- AJ

a (ksi)

0 _0,8

e

Gambar 1 -1 7 Diagram tegangan­ regangan untuk tembaga yang mengalami tekan

mate sebenarnya. Baja berkadar karbon tinggi mempunyai tegangan luluh tinggi - kadang-kadang melebihi 1 00 ksi (700 MPa) - tetapi berperilaku getas dan fraktur selalu terjadi pada perpanjangan yang hanya beberapa persen.

Kaca biasa merupakan bahan getas yang hampir ideal karena bahan ini menunjukkan tidak adanya daktilitas sedikitpun. Kurva tegangan­ regangan untuk kaca yang mengalami tarik pacta dasarnya adalah garis lurus, dengan kegagalan muncul sebelum luluh terjadi. Tegangan ultimatenya sekitar 1 0000 psi (70 MPa) untuk beberapa jenis kaca plat, tetapi ada variasi yang cukup besar, bergantung pacta jenis kaca, ukuran benda uji, dan adanya cacat mikroskopis. Serat kaca dapat mempunyai kekuatan yang sangat tinggi, dan tegangan ultimatenya dapat melebihi 1 .000.000 psi (7 GPa).

Banyak jenis plastik yang digunakan untuk maksud struktural karena bahan ini ringan, tahan karat, dan mempunyai insulasi elektrikal yang baik. Sifat mekanisnya sangat bervariasi. dimana beberapa jenis plastik bersifat getas dan 1ainnya bersifat daktil. Dalam mendesain dengan plastik, perlu diingat bahwa besarannya sangat dipengaruhi perubahan temperatur dan berjalannya waktu. Sebagai contoh, tegangan tarik ultimate beberapa jenis plastik dapat menjadi tinggal setengahnya apabila temperatumya meningkat dari 50°F ke 120°F. Juga, plastik yang dibebani dapat meregang secara gradual dengan bertambahnya waktu sampai bahan itu tidak dapat berfungsi lagi. Sebagai contoh, sebuah batang yang terbuat dari polivinil khlorida yang mengalami beban tarik yang semula menghasilkan regangan 0,005 dapat mengalarni regangan sebesar dua kalinya setelah seminggu, meskipun beban tersebut konstan. (Fenomena ini, dikenal dengan rangkak, dibahas pacta bagian berikut.)

Tegangan tarik ultimate untuk plastik pada umumnya ada dalam selang 2 sampai 50 ksi ( 1 4 sampai 350 MPa) dan berat jenisnya bervariasi dari 50 sampai 90 lb/ft3 (8 sampai 1 4 kN/m3). Ada sejenis nilon yang mem­ punyai tegangan ultimate sebesar 12 ksi (80 MPa) dan beratnya hanya 70 lb/fe ( 1 1 kN/m3), yang berarti hanya 12% lebih berat daripada air. Karena ringannya, maka rasio kekuatan terhadap berat untuk bahan nilon kurang lebih sama dengan baja struktural (lihat Soal 1 .3-6).

Bahan yang diperkuat filamen terdiri atas bahan dasar (atau matriks) dengan kandungan serat dan filamen yang berkekuatan tinggi. Komposit yang dihasilkannya mempunyai kekuatan yang jauh lebih tinggi di­ bandingkan bahan dasarnya. Sebagai contoh, penggunaan serat kaca dapat meningkatkan kekuatan hingga dua kali kekuatan matriks plastik. Komposit banyak digunakan dalam pesawat terbang, perahu, roket, dan pesawat luar angkasa di mana kekuatan tinggi dan bobot yang ringan dibutuhkan.

1 8 Bab 1 Tarik, Tekan, dan Geser

bahwa kurva tegangan-regangan menjadi sangat curam). Karakteristik ini diilustrasikan dalam Gambar 1 -17, yang memperlihatkan diagram tegangan­ regangan tekan untuk tembaga. Karena luas penampang aktual dari benda uji tekan lebih besar daripada luas awal, maka tegangan sebenarnya pada pengujian tekan akan lebih kecil daripada tegangan nominal.

Bahan getas yang dibebani tekan pada umumnya mempunyai daerah linier awal yang diikuti dengan daerah di mana perpendekannya bertambah dengan laju yang lebih besar daripada bebannya. Kurva tegangan-regangan untuk tekan dan tarik seringkali mempunyai bentuk yang serupa, tetapi tegangan ultimatenya dalam keadaan tekan jauh lebih besar daripada ke­ adaan tarik. Juga, tidak seperti bahan daktil, yang membesar tengahnya apa­ bila ditekan, bahan getas secara aktual akan pecah pada beban maksimum.

Tabel besaran mekanis untuk beberapa bahan diberikan dalam Lampiran H di belakang buku ini. Data di dalam tabel tersebut merupakan data tipikal bahan dan dapat digunakan untuk memecahkan soal-soal dalam buku ini. Sekalipun demikian, besaran bahan dan kurva tegangan-regangan sangat bervariasi, bahkan untuk bahan yang sama, karena berbedanya proses pembuatan, komposisi kimiawi, cacat internal, temperatur, dan berbagai faktor lain. Karena itu, data yang diperoleh dari Lampiran H (atau tabel-tabel lain yang serupa) sebaiknya tidak digunakan untuk tujuan rekayasa atau desain yang khusus. Sebagai gantinya, pembuat bahan atau penyalumya perlu dimintai informasi tentang produk khusus tersebut.

ELASTISITAS, PLASTISITAS, DAN RANGKAK

Kurva tegangan-regangan menunjukkan perilaku bahan teknik apabila bahan tersebut dibebani tarik atau tekan, sebagaimana dibahas pada subbab sebelum ini. Untuk melangkah lebih jauh, mari kita tinjau apa yang terjadi apabila beban dihilangkan dan bahan tersebut tak berbeban. Anggap, sebagai contoh, bahwa kita menerapkan beban tarik pada benda uji sedemi­ kian hingga tegangan dan regangan berjalan dari titik pusat 0 ke titik A pada kurva tegangan-regangan dalam Gambar 1 - 1 8a. Anggap pula bahwa apabila beban itu dihilangkan, maka bahan akan benar-benar mengikuti kurva yang sama dan kembali ke asal 0. Sifat bahan seperti ini, yaitu dapat kembali ke dimensi semula selama beban dihilangkan, disebut elastisitas, dan bahan itu sendiri disebut elastis. Catat bahwa kurva tegangan-regangan dari 0 ke A tidak harus linier agar bahan dapat disebut elastis.

(J I _F

Gambar 1 -19 Pembebanan kem­ bali pada bahan dan meningkatnya , limit proporsional dart elastis

batang akan sebagian kemba1i ke bentuk semu1a, dan bahan ini disebut elastis sebagian.

Di antara titik A dan B pada kurva teganganregangan (Gambar 1 -1 8b ) , pasti ada sebuah titik di mana bahan sebelumnya elastis, dan sesudah­ nya elastis sebagian. Untuk mencari titik tersebut, kita bebani bahan hingga mencapai tegangan yang telah dipilih untuk kemudian menghilangkan beban tersebut. Jika tidak ada set yang permanen (artinya perpanjangan batang tersebut kembali ke nol), maka bahan itu e1astis penuh sampai harga tegangan yang dipilih. Proses pembebanan dan penghilangan beban ini diulangi terns untuk tegangan yang lebih besar. Akhimya, akan diperoleh tegangan yang menyebabkan sebagian regangannya tidak dapat pulih pada saat penghilangan beban. Dengan menggunakan prosedur ini, tegangan pada limit atas dari daerah elastis dapat dihitung, misalnya, tegangan di titik E dalam Gambar 1 - 1 8a dan b. Tegangan di titik ini dikenal sebagai limit elastis dari suatu bahan.

Ban yak bahan, termasuk hampir semua metal. yang mempunyai daerah linier di awal kurva tegangan-regangannya ( sebagai contoh, lihat Gambar 1 - 1 0 dan 1 - 13). Tegangan di limit atas daerah linier ini merupakan limit proporsional. Limit elastis ini biasanya sama dengan, atau sedikit di atas, limit proporsional. Dengan demikian, untuk sebagian besar bahan kedua limit tersebut dianggap mempunyai nilai numerik yang sama. Pada baja lunak, tegangan luluhnya juga sangat dekat dengan limit proporsiona1 sehingga untuk praktisnya, tegangan luluh, limit elastis, dan limit proporsional diasumsikan sama. Tentu saja, situasi ini tidak berlaku untuk semua bahan. Karet adalah contoh nyata untuk bahan yang tetap bersifat elastis meskipun limit proporsionalnya telah dilampaui.

Karakteristik suatu bahan yang mana bahan itu dapat mengalami regangan inelastis melewati regangan pada limit elastis disebut plastisitas. Jadi, pada kurva tegangan-regangan dalam Gambar 1 - l Sa, kita mempunyai daerah elastis yang diikuti dengan daerah plastis. Apabila deformasi besar terjadi pada bahan daktil yang dibebani hingga daerah p1astis, maka bahan ini disebut mengalami aliran plastis.

Jika suatu bahan masih berada dalam daerah elastis, bahan tersebut dapat dibebani, dihilangkan bebannya, dan dibebani lagi tanpa adanya perubahan signifikan pada perilakunya. Tetapi, apabila dibebani hingga daerah plastis, struktur internal bahan tersebut akan berubah dan besaran bahannya juga berubah. Sebagai contoh, kita telah mengamati bahwa ada regangan permanen di benda uji sesudah penghilangan beban dari daerah plastis (Gambar 1 - 1 8b). Sekarang bayangkan bahwa bahan ini dibebani kembali sesudah penghilangan beban tersebut (Gambar 1 - 19). Pembebanan yang baru ini dimu1ai di titik C pada diagram dan terus mengarah ke atas hingga titik B, titik di mana penghilangan beban dimulai pada siklus pembebanan pertama. Bahan tersebut selanjutnya mengikuti diagram tegangan-regangan hingga titik F. Jadi, untuk pembebanan kedua, kita dapat membayangkan bahwa kita mempunyai kurva tegangan-regangan dengan titik pusat di titik C.