Penerbit Fakultas Keguruan dan Ilmu Pendidikan (FKIP) Universitas Syiah Kuala
Linda Vitoria, S.Si., M.Sc.
TEORI BILANGAN UNTUK
MAHASISWA PGSD
i
TEORI BILANGAN UNTUK MAHASISWA PGSD
Linda Vitoria, S.Si., M.Sc.
Penerbit Fakultas Keguruan dan Ilmu Pendidikan (FKIP) Universitas Syiah Kuala
ii Teori Bilangan untuk Mahasiswa PGSD
Penulis:
Linda Vitoria, S.Si., M.Sc. Editor:
Dra. Monawati, M.Pd. Hak cipta 2019 pada Penulis.
Hak cipta dilindungi undang-undang.
Dilarang memperbanyak sebagian atau seluruh isi buku ini dalam bentuk apapun tanpa izin tertulis dari pemegang hak cipta/Penerbit. Diterbitkan oleh:
Penerbit Fakultas Keguruan dan Ilmu Pendidikan (FKIP) Universitas Syiah Kuala
Jalan Tgk. Hasan Krueng Kale Darussalam, Banda Aceh 23111
Telepon 085260002082, Faximile 06517551407
Homepage: www.fkip.unsyiah.ac.id E-mail: [email protected]
Perpustakaan Nasional RI: Katalog dalam Terbitan (KDT) Linda Vitoria.
Teori Bilangan untuk Mahasiswa PGSD. -- Banda Aceh : Penerbit Fakultas Keguruan dan Ilmu Pendidikan (FKIP) Universitas Syiah Kuala, 2019.
v, 95 hlm.; 15,5 cm x 23 cm. ISBN: 978-602-73716-9-9
iii
KATA PENGANTAR
Buku ini disusun sebagai buku referensi mahasiswa Pendidikan Guru Sekolah Dasar (PGSD) dalam mengikuti matakuliah Teori Bilangan. Pembahasan teori bilangan diperlukan untuk memperkuat pemahaman mahasiswa PGSD sebagai calon guru sekolah dasar mengenai aturan-aturan yang berlaku pada bilangan.
Materi-materi yang dikaji meliputi sifat-sifat dan teorema-teorema yang berlaku pada sistem bilangan bulat seperti aturan penjumlahan, pengurangan, perkalian, dan pembagian; urutan bilangan bulat; keterbagian; faktor persekutuan terbesar (FPB) dan kelipatan persekutuan terkecil (KPK); dan kekongruenan.
Buku ini dirancang sedemikian rupa sehingga menuntut keaktifan mahasiswa dalam mengerjakan contoh-contoh dan soal-soal latihan. Dengan demikian diharapkan mahasiswa dapat membangun pemahamannya secara mandiri tentang materi-materi teori bilangan.
Banda Aceh, Januari 2019 Penulis
iv
DAFTAR ISI
1. PENDAHULUAN ... 1 2. HIMPUNAN BILANGAN ... 5 Soal Latihan ... 9 3. BILANGAN PRIMA ... 11 Soal Latihan ... 134. OPERASI HITUNG PADA BILANGAN ... 15
4.1 Operasi Hitung pada Bilangan Cacah ... 15
4.2 Operasi Hitung pada Bilangan Bulat ... 18
4.3 Operasi Hitung Bilangan Rasional ... 19
4.4 Sifat Komutatif (Pertukaran) ... 20
4.5 Sifat Asosiatif (Pengelompokan) ... 23
4.6 Unsur Identitas ... 25 4.7 Invers ... 28 4.8 Sifat Distributif ... 29 4.9 Sifat Ketertambahan. ... 30 4.10 Sifat Ketergandaan ... 31 4.11 Sifat Kanselasi ... 31 Soal Latihan ... 32
5. ATURAN PENJUMLAHAN, PENGURANGAN, PERKALIAN DAN PEMBAGIAN BILANGAN BULAT ... 34
5.1 Aturan Penjumlahan dan Pengurangan Bilangan Bulat ... 34
Soal Latihan ... 36
5.2 Aturan Perkalian Bilangan Bulat ... 36
Soal Latihan ... 38
5.3 Aturan Pembagian Bilangan Bulat ... 38
Soal Latihan ... 45
6. URUTAN BILANGAN BULAT ... 46
Soal Latihan ... 52
7. KETERBAGIAN BILANGAN BULAT ... 54
Soal Latihan ... 57
8. FAKTOR PERSEKUTUAN TERBESAR (FPB) ... 59
Algoritma Pembagian ... 62
Soal Latihan ... 68
9. KELIPATAN PERSEKUTUAN TERKECIL (KPK) ... 70
v
10. HUBUNGAN FPB DAN KPK DARI DUA BILANGAN .... 74
Soal Latihan ... 77 11. KEKONGRUENAN BILANGAN ... 78 Soal Latihan ... 90 DAFTAR PUSTAKA ... 91 GLOSARIUM ... 92 INDEKS ... 94
1
1. PENDAHULUAN
Kajian mata kuliah Teori Bilangan pada buku ajar ini membahas aturan-aturan yang berlaku pada sistem bilangan, khususnya sistem bilangan bulat. Terdapat beberapa istilah yang sering digunakan dalam pembahasan teori bilangan. Untuk memudahkan pembaca, berikut disajikan beberapa istilah yang lazim digunakan dalam teori bilangan dan pembahasannya.
1. Angka dan bilangan
Bilangan menyatakan banyaknya anggota suatu himpunan, sedangkan angka adalah lambang bilangan.
Contohnya:
a. Terdapat lima buah pensil di atas meja.
Bilangan lima dapat dilambangkan dengan angka 5 atau V (angka romawi).
b. Bilangan 4.537 terdiri dari 4 angka, yaitu angka 4, 5, 3 dan 7.
c. Bilangan VI terdiri dari 2 angka, yaitu angka V dan I. d. Penjumlahan dua buah bilangan tiga angka artinya
penjumlahan yang melibatkan dua bilangan yang masing-masing terdiri atas tiga angka, misalnya 225 + 314.
2. Sistem desimal
Sistem desimal merupakan salah satu metode penulisan bilangan. Dalam sistem desimal digunakan pengelompokan
2 bilangan dengan basis sepuluh, yaitu pengelompokan ke dalam sepuluh-sepuluh.
Lambang bilangan pada sistem desimal terdiri atas sepuluh angka yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9.
Penulisan lambang bilangan pada sistem desimal didasarkan pada nilai tempat angkanya.
Lambang “30” menyatakan tigapuluh, yaitu 3 puluhan dan 0 satuan.
Lambang “270” menyatakan bilangan dua ratus tujuh puluh, yaitu 2 ratusan, 7 puluhan, dan 0 satuan.
Lambang “1445” menyatakan 1 ribuan, 4 ratusan, 4 puluhan, dan 5 satuan. Di sini, angka 4 pada ratusan tidak sama nilainya dengan angka 4 pada puluhan, karena perbedaan nilai tempatnya.
3. Notasi
Notasi adalah cara menuliskan atau melambangkan sesuatu sesuai dengan kesepakatan yang berlaku. Misalnya:
untuk menyatakan bilangan dua puluh lima, notasinya adalah 25 atau 20 + 5;
untuk menyatakan “lebih dari” notasinya adalah “>”. Contohnya: 0 > –3, dibaca “0 lebih besar dari negatif 3”.
notasi untuk operasi penjumlahan adalah +
notasi untuk operasi pengurangan adalah –
notasi perkalian adalah ×
3 4. Faktor dan Kelipatan
Suatu bilangan 𝑎 dikatakan faktor dari bilangan 𝑏 apabila 𝑎 membagi habis 𝑏 tanpa sisa. Contohnya, 2 adalah faktor dari 8 karena 2 habis membagi 8 tanpa sisa.
Yaitu 8 ÷ 2 = 4, sisa = 0. Atau ditulis 8 2= 4.
3 bukan faktor dari 16 karena 3 tidak membagi habis 16. Yaitu 16 ÷ 3 = 5, sisa = 1.
Atau ditulis 16 3 = 5
1 3.
Suatu bilangan 𝑎 dikatakan kelipatan dari bilangan 𝑏 jika 𝑎 diperoleh dari mengalikan 𝑏 dengan bilangan lain.
Contohnya, 8 adalah kelipatan dari 2 karena 8 diperoleh dari mengalikan 2 dengan 4.
Atau ditulis 8 = 2 x 4.
12 adalah juga kelipatan dari 2 karena 12 = 2 x 6.
4 dan 6 juga kelipatan dari 2. Jika didata kelipatan dari 2 adalah 2, 4, 6, 8, 10, 12, 14, dst.
Kelipatan dari 1 adalah 1, 2, 3, 4, … Kelipatan dari 3 adalah 3, 6, 9, 13, … Kelipatan dari 15 adalah 15, 30, 45, 60, ….
5. Faktorisasi yaitu menguraikan menjadi faktor-faktor. Misalnya 12 dapat difaktorisasi menjadi: 12 = 2 x 6; 12 = 3 x 4; 12 = 3 x 2 x 2.
4 6. Algoritma
Algoritma artinya prosedur penyelesaian suatu masalah secara bertahap. Istilah algoritma diambil dari nama Al-Khwarizmi, seorang ahli matematika berkebangsaan Arab.
7. Teorema
Teorema merupakan sebuah pernyataan yang dapat dibuktikan berdasarkan asumsi-asumsi yang telah disetujui. Contoh teorema yang terkenal adalah Teorema Pythagoras yang mengatakan bahwa pada suatu segitiga siku-siku, kuadrat sisi miring sama dengan jumlah kuadrat kedua sisi yang lain.
8. Aksioma
Yaitu pernyataan yang diterima sebagai kebenaran tanpa memerlukan bukti.
Contohnya: melalui dua titik A dan B hanya dapat dibuat satu garis lurus saja.
5
2. HIMPUNAN BILANGAN
Tujuan Pembelajaran
1. Mahasiswa mampu mengidentifikasi klasifikasi suatu bilangan.
2. Mahasiswa mampu menyatakan pecahan dalam bentuk desimal dan persen, dan sebaliknya.
Secara garis besar, bilangan dikelompokkan menjadi dua himpunan yaitu himpunan bilangan real dan himpunan bilangan imajiner. Himpunan bilangan imajiner atau bilangan khayal terdiri atas bilangan √−1. Sedangkan himpunan bilangan riil atau bilangan nyata terdiri atas bilangan-bilangan lain selain √−1.
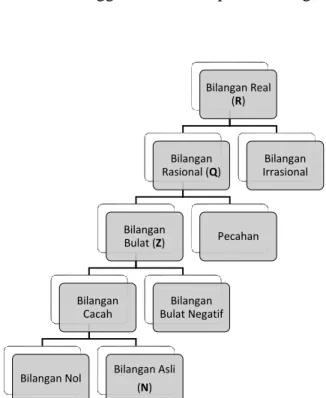
Diagram berikut ini menggambarkan himpunan bilangan real.
Bilangan Real (R) Bilangan Rasional (Q) Bilangan Bulat (Z) Bilangan Cacah
Bilangan Nol Bilangan Asli (N) Bilangan Bulat Negatif Pecahan Bilangan Irrasional
6 Berikut penjelasan dari diagram di atas, dimulai dari bilangan terkecil yaitu bilangan nol.
Bilangan Nol dilambangkan dengan “0” menyatakan tidak ada.
Bilangan Asli dilambangkan dengan N (Natural Numbers) yaitu bilangan yang digunakan untuk membilang banyak benda. N = {1, 2, 3, 4, 5, 6, 7, …}
Bilangan asli dapat dikelompokkan menjadi 3 bagian, yaitu: 1) Unit, terdiri atas bilangan 1.
2) Bilangan prima, yaitu bilangan asli yang mempunyai tepat 2 faktor saja yaitu 1 dan bilangan itu sendiri. Contoh bilangan prima adalah 2, 3, 5, 7, 11, dan seterusnya. 3) Bilangan komposit, yaitu bilangan asli yang mempunyai
lebih dari 2 faktor. Contohnya: 4, 6, 8, 9, 10, dan seterusnya.
Berdasarkan habis dibagi 2, bilangan asli juga dapat dikelompokkan menjadi bilangan genap dan bilangan ganjil. 1) Bilangan genap, yaitu bilangan asli yang habis dibagi 2
seperti 2, 4, 6, 8, dan seterusnya.
2) Bilangan ganjil, yaitu bilangan asli yang tidak habis dibagi 2 seperti 3, 5, 7, 9, dan seterusnya.
Bilangan Cacah yaitu himpunan bilangan yang terdiri atas 0 dan bilangan asli. Bilangan cacah = {0, 1, 2, 3, 4, 5, 6, 7, 8, …}.
7 Bilangan Bulat atau Integer dilambangkan dengan I (integer) atau Z (Zahlen, yaitu bahasa Jerman yang artinya ‘bilangan’). Bilangan bulat terdiri atas bilangan cacah dan bilangan bulat negatif. Anggota himpunan bilangan bulat adalah:
Z = { …, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, …}.
Bilangan Rasional dilambangkan dengan Q (Quotient) merupakan bilangan yang dapat ditulis sebagai pembagian dua bilangan bulat 𝑝
𝑞 dengan 𝑞 ≠ 0. Notasi untuk bilangan rasional adalah:
Q = {𝑝
𝑞, 𝑝 𝑑𝑎𝑛 𝑞 ∈ 𝒁, 𝑞 ≠ 0}. Beberapa contoh bilangan rasional: 1
3 , 5, –2, 0, − 4
5 , 1000, dan lain-lain.
Bilangan rasional dapat dinyatakan dalam bentuk pecahan biasa, bentuk desimal dan persen.
Contoh:
a. Nyatakan bentuk pecahan biasa dan bentuk persen berikut ini ke dalam bentuk desimal.
1 2= 0,5 75% = 75 100 = 0,75 1 10= 0,1 20% = 20 100= 0,2 1 100 = 0,01 33% = 33 100= 0,33 1 1000= 0,001 2,5% = 2,5 100= 25 1000= 0,025 23 10= 2,3 8% = 8 100= 0,08
8 b. Nyatakan bentuk desimal berikut ke dalam bentuk
pecahan. 0,5 = 5 10= 1 2 2,3 = 23 10= 2 3 10 0,25 = 25 100= 1 4 2,70 = 2 70 100= 2 7 10 24,5 = 24 5 10= 24 1 2 12,25 = 12 25 100= 12 1 4
c. Nyatakan bentuk pecahan dan desimal berikut ke dalam bentuk persen.
1
2= 50%
Perhitungannya sebagai berikut: 1 2=
1
2 𝑥 100% = 50% 0,4 = 40%
Perhitungannya sebagai berikut: 0,4 = 0,4 𝑥 100% = 40% 3 5= 3 5× 100% = 60% 0,25 = 0,25 × 100% = 25%.
Bilangan Irrasional adalah bilangan yang tidak dapat ditulis sebagai pembagian dua bilangan bulat. Contohnya 𝜋. Bilangan 𝜋 adalah rasio keliling suatu lingkaran dengan diameternya. Nilai bilangan 𝜋 = 3,14159265358979323846 …. Bilangan
9 𝜋 ini tidak dapat dinyatakan dalam bentuk pembagian dua bilangan bulat. Dengan kata lain, tidak ada bentuk pecahan untuk 𝜋. Tapi, untuk memudahkan dalam perhitungan, biasanya diambil nilai pendekatan 𝜋 yaitu 22
7 atau 3,14. Contoh lain bilangan irrasional adalah √2 .
Bilangan Real dilambangkan dengan R merupakan gabungan dari semua bilangan di atas. Bilangan real atau bilangan nyata adalah lawan dari bilangan imajiner atau bilangan khayal. Bilangan imajiner dilambangkan dengan I yaitu √−1 .
Soal Latihan
1. Diantara pernyataan-pernyataan berikut ini, manakah yang benar? a. 0 ∈ 𝑵 b. −1 5∈ 𝒁 c. −3 ∈ 𝒁 d. 100 ∈ 𝑸 e. √5 ∈ 𝑹
2. Lengkapilah tabel berikut ini.
No. Pecahan Desimal Persen
a 3
10 b 0,1 c 24% d 1,50 e 4 5
11
3. BILANGAN PRIMA
Tujuan Pembelajaran
Mahasiswa mampu menentukan suatu bilangan adalah bilangan prima atau komposit.
Pada bab sebelumnya telah dibahas himpunan-himpunan bilangan. Pada bab ini akan dikaji lebih mendetil tentang bilangan prima. Sebagaimana telah disebutkan sebelumnya, bilangan prima adalah bilangan asli yang lebih besar dari 1 yang hanya habis dibagi oleh 1 dan bilangan itu sendiri. Dengan kata lain, bilangan prima hanya mempunyai dua faktor. Contoh bilangan prima: 2, 3, 5, 7, 11, 13, 17, 19, 29, dst.
Berikut ini adalah beberapa teorema yang berlaku pada bilangan prima.
1. Setiap bilangan asli yang lebih besar dari 1 dapat dibagi oleh suatu bilangan prima.
Coba berikan contohnya.
2. Setiap bilangan asli yang lebih besar dari 1 adalah bilangan prima atau bilangan itu dapat dinyatakan sebagai perkalian bilangan-bilangan prima.
12 Untuk memeriksa apakah suatu bilangan 𝑛 adalah prima atau bukan, coba bagi 𝑛 dengan bilangan-bilangan prima yang kurang dari √𝑛. Apabila 𝑛 tidak habis dibagi oleh bilangan-bilangan prima tersebut, maka 𝑛 adalah bilangan prima. Namun apabila 𝑛 habis dibagi oleh bilangan-bilangan prima tersebut, maka 𝑛 bukan bilangan prima.
Contoh: apakah 109 prima?
Jawab:
√𝑛 = √109 = 10,44
Kita periksa dengan membagi 109 dengan bilangan-bilangan prima yang lebih kecil dari 10 yaitu 2, 3, 5, dan 7.
109 ÷ 2 = 54,5 109 ÷ 3 = 36,3 109 ÷ 5 = 21,8 109 ÷ 7 = 15,57
Tampak bahwa 109 tidak habis dibagi oleh semua bilangan-bilangan prima di atas. Itu artinya 109 adalah bilangan-bilangan prima.
Contoh lain, apakah 2191 bilangan prima?
Jawab:
√𝑛 = √2191 = 46,81
Kita periksa dengan membagi 2191 dengan bilangan-bilangan prima yang lebih kecil dari 46 yaitu 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, dan 43.
13 2191 ÷ 3 = 730,33
2191 ÷ 5 =438,2 2191 ÷ 7 = 313
Ternyata 2191 habis dibagi 7, hasilnya 313. Ini artinya 7 dan 313 adalah faktor dari 2191. Jadi faktor-faktor dari 2191 adalah 1, 7, 313, dan 2191. Karena 2191 memiliki lebih dari 2 faktor, maka 2191 bukan bilangan prima.
Soal Latihan
1. Manakah yang saling prima? a. 4 dan 6
b. 8 dan 18 c. 15 dan 42 d. 12 dan 25
2. Untuk menentukan apakah 1027 merupakan bilangan prima atau bukan, dapat ditunjukkan ada atau tidaknya bilangan-bilangan prima yang membagi 1027. Bilangan-bilangan-bilangan prima itu adalah yang …
a. Kurang dari 1027 b. Kurang dari 32 c. Kurang dari 100 d. kurang dari 10
14 3. Dari bilangan-bilangan berikut ini, yang merupakan
bilangan prima adalah … a. 117
b. 237 c. 357 d. 227
4. Dari bilangan-bilangan berikut ini, yang merupakan bilangan komposit adalah …
a. 37 b. 137
c. 237 d. 337
15
4. OPERASI HITUNG PADA BILANGAN
Tujuan Pembelajaran
Mahasiswa mampu menerapkan sifat-sifat penjumlahan, pengurangan, perkalian dan pembagian dalam menyelesaikan soal-soal operasi hitung bilangan.
Pada himpunan bilangan riil dapat dilakukan operasi-operasi hitung seperti penjumlahan, pengurangan, perkalian, pembagian, penarikan akar, perpangkatan, dan lain-lain. Berikut ini akan dibahas beberapa definisi yang berkaitan dengan operasi hitung pada bilangan, dimulai dari bilangan cacah.
4.1 Operasi Hitung pada Bilangan Cacah
1. Misalkan p dan q adalah bilangan cacah. Penjumlahan p dan q ditulis p + q. Hasilnya adalah cacah gabungan himpunan yang memiliki p buah anggota dan himpunan yang memiliki q buah anggota. Contoh: 3 + 5 = 8 15 + 28 = .... 7 + .... = 16 .... + .... = 27 .... + .... = ....
Operasi penjumlahan bilangan cacah bersifat tertutup, artinya hasil penjumlahan dua bilangan cacah adalah bilangan cacah juga.
16 2. Operasi pengurangan merupakan lawan dari operasi penjumlahan. Pengurangan bilangan cacah p – q = r adalah
lawan dari penjumlahan q + r = p. Dapat ditulis, p – q = r ⇔ p = q + r. Dibaca: p – q = r jika dan hanya jika
p = q + r.
Contoh: 5 – 2 = 3 ⇔ 5 = 2 + 3 6 – 4 = .... ⇔ 6 = 4 + .... 7 – .... = .... ⇔ 7 = .... + .... .... – .... = .... ⇔ .... = .... + ....
Bagaimana dengan pengurangan dua bilangan yang sama? Contoh: 12 – 12 = 0 ⇔ 12 = 12 + 0
6 – 6 = 0 .... – .... = 0
Dapat disimpullkan bahwa pengurangan dua bilangan yang sama menghasilkan 0. Secara umum dapat ditulis p – p = 0.
Operasi pengurangan bilangan cacah tidak memenuhi sifat tertutup. Hal ini karena hasil pengurangan dua bilangan cacah bisa berupa bilangan cacah, namun bisa juga bukan bilangan cacah. Coba berikan contohnya.
3. Operasi perkalian dua bilangan cacah p × q adalah penjumlahan berulang q sebanyak p kali. Ditulis:
p × q = q + q + q + ... + q
17 contohnya: 2 × 4 = 4 + 4 = 8 4 × 2 = 2 + 2 + 2 + 2 = 8 3 × 5 = .... + .... + .... = .... 5 × 6 = .... + .... + .... + .... + .... = .... 7 × 1 =
Operasi perkalian bilangan cacah memenuhi sifat tertutup. 4. Operasi pembagian merupakan kebalikan dari operasi
perkalian. Pembagian dua bilangan cacah p ÷ q = r adalah kebalikan dari p = q × r. Ditulis, p ÷ q = r ⇔ p = q × r. Dibaca: p ÷ q = r jika dan hanya jika p = q × r.
Contoh: 12 ÷ 3 = 4 ⇔ 12 = 3 × 4 10 ÷ 2 = .... ⇔ 10 = 2 × .... 21 ÷ .... = 7 ⇔ 21 = .... × 7 .... ÷ .... = 6 ⇔ .... = .... × 6 .... ÷ .... = .... ⇔ .... = .... × ....
Bagaimana hasil pembagian dua bilangan yang sama? Contoh: 2 ÷ 2 = 1 ⇔ 2 = 2 × 1
3 ÷ 3 = .... .... ÷ .... = ....
Dapat disimpulkan bahwa pembagian dua bilangan yang sama menghasilkan 1. Secara umum dapat ditulis p ÷ p =1.
18 Operasi pembagian bilangan cacah tidak bersifat tertutup karena hasil pembagiannya bisa berupa bilangan cacah, namun bisa pula bukan bilangan cacah. Berikan contohnya.
4.2 Operasi Hitung pada Bilangan Bulat
Himpunan bilangan bulat merupakan perluasan dari himpunan bilangan cacah. Himpunan bilangan bulat terdiri atas bilangan cacah dan bilangan bulat negatif. Definisi-definisi serta sifat-sifat operasi hitung yang berlaku pada bilangan cacah juga berlaku pada bilangan bulat ditambah dengan sedikit perluasan.
Penjumlahan dan perkalian bilangan bulat memenuhi sifat tertutup, sama seperti bilangan cacah. Namun, sifat pengurangan bilangan bulat berbeda dengan pengurangan bilangan cacah. Pengurangan bilangan cacah tidak bersifat tertutup sedangkan pengurangan bilangan bulat bersifat tertutup. Hal ini karena pengurangan dua bilangan bulat menghasilkan bilangan bulat pula. Contohnya, 3 – 2 = ....
4 – 5 = .... 2 – (–3) = .... –6 – 7 = ....
Bagaimana dengan operasi pembagian bilangan bulat, apakah memenuhi sifat tertutup? Perhatikan contoh berikut.
19 3 ÷ 2 = ....
–12 ÷ 6 = .... –9 ÷ 4 = ....
Dari contoh-contoh di atas, apa yang dapat Anda simpulkan tentang sifat pembagian bilangan bulat?
4.3 Operasi Hitung Bilangan Rasional
Himpunan bilangan rasional merupakan perluasan dari himpunan bilangan bulat. Himpunan bilangan rasional terdiri atas bilangan bulat dan pecahan. Definisi-definisi serta sifat-sifat operasi hitung yang berlaku pada bilangan bulat juga berlaku pada bilangan rasional ditambah dengan sedikit perluasan.
Pada bilangan bulat, penjumlahan, pengurangan, dan perkalian memenuhi sifat tertutup. Hal ini juga berlaku pada bilangan rasional. Pembagian bilangan bulat tidak memenuhi sifat tertutup, namun pembagian bilangan rasional memenuhi sifat tertutup karena hasil pembagian dua bilangan rasional adalah bilangan rasional pula.
Contohnya, 14 ÷ 7 = .... 5 ÷ 15 = .... –8 ÷ 0,5 = .... 3 ÷1 5 = .... 2 3 ÷ 1 4 = ....
20 Disamping sifat tertutup yang dibahas di atas, terdapat sifat-sifat operasi hitung lainnya yaitu sifat komutatif, asosiatif, distributif, unsur identitas dan invers. Berikut akan dibahas satu persatu.
4.4 Sifat Komutatif (Pertukaran)
Urutan mengerjakan sesuatu terkadang mempengaruhi hasil. Misalnya memakai kaus kaki sebelum memakai sepatu berbeda hasilnya jika urutannya diubah, yaitu memakai sepatu dulu baru kaus kaki. Tetapi, terkadang urutan tidak mempengaruhi hasil. Misalnya saat membuat segelas air manis, memasukkan gula sebelum air maupun memasukkan air sebelum gula, hasilnya tetap sama. Begitu pula bila kita berjalan 3 langkah, lalu berjalan lagi 5 langkah, hasilnya akan sama jika kita berjalan 5 langkah terlebih dahulu, kemudian 3 langkah. Pada operasi hitung, apabila urutan pengerjaan tidak mempengaruhi hasil (tetap memberikan hasil yang sama), maka operasi seperti itu dikatakan bersifat komutatif.
Untuk memeriksa sifat komutatif operasi hitung pada bilangan riil, lengkapilah tabel berikut ini dan bandingkan hasil pada kolom kiri dan kolom kanan.
Penjumlahan 4 + 7 = 2 + (–3) = 7 + 4 = –3 + 2 =
21 5,2 + 6,9 = –4,6 + 0,8 = 1 + 3 4 = 6,9 + 5,2 = 0,8 + (–4,6) = 3 4 + 1 = Pengurangan 4 – 7 = 2 – (–3) = 5,2 – 6,9 = –4,6 – 0,8 = 1 – 3 4 = 7 – 4 = –3 – 2 = 6,9 – 5,2 = 0,8 – (–4,6) = 3 4 – 1 = Perkalian 4 × 7 = 2 × (–3) = 5,2 × 6,9 = –4,6 × 0,8 = 4 × 7 = 2 × (–3) = 5,2 × 6,9 = –4,6 × 0,8 =
22 1 × 3 4 = 1 × 3 4 = Pembagian 6 ÷ 3 = 8 ÷ (–2) = 4 ÷ 0,5 = 3 ÷ 6 = –2 ÷ 8 = 0,5 ÷ 4 =
Dari tabel di atas dapat disimpulkan bahwa operasi penjumlahan memenuhi sifat komutatif. Secara umum ditulis, 𝑝 + 𝑞 = 𝑞 + 𝑝.
Apakah operasi perkalian memenuhi sifat komutatif? Secara umum dapat ditulis, 𝑝 × 𝑞 = .... × ....
Apakah operasi pengurangan memenuhi sifat komutatif? Apakah operasi pembagian memenuhi sifat komutatif?
Sifat komutatif dapat memudahkan kita pada saat melakukan operasi hitung penjumlahan dan perkalian. Contohnya, 6 + 148. Soal ini lebih mudah dihitung dengan menukarkan tempat kedua suku penjumlahan menjadi 148 + 6. Dengan cara bersusun ke bawah dapat ditulis,
148 6 + ....
23 Untuk perkalian contohnya, 34 × 1652. Soal ini juga lebih mudah dihitung dengan menukarkan tempatnya menjadi
1652 34 × ...
4.5 Sifat Asosiatif (Pengelompokan)
Hasil penjumlahan tiga bilangan tidak bergantung pada cara kita mengelompokkan ketiga bilangan tersebut. Contohnya, penjumlahan 2 + 3 + 4 dapat dilakukan dengan menjumlahkan 2 + 3 terlebih dahulu kemudian hasilnya dijumlahkan dengan 4; dapat pula dilakukan dengan menjumlahkan 3 + 4 terlebih dahulu, baru kemudian dijumlahkan dengan 2. Cara yang pertama ditulis sebagai berikut.
(2 + 3) + 4
Sedangkan cara yang kedua ditulis sebagai berikut. 2 + (3 + 4)
Keduanya memberikan hasil yang sama. Yaitu (2 + 3) + 4 = 2 + (3 + 4) = 9. Oleh karena itu dikatakan operasi penjumlahan memenuhi sifat asosiatif. Secara umum ditulis, (𝑝 + 𝑞) + 𝑟 = 𝑝 + (𝑞 + 𝑟).
Untuk memeriksa apakah pengurangan, perkalian, dan pembagian juga memenuhi sifat asosiatif, lengkapilah tabel berikut ini kemudian bandingkan hasil di kolom kanan dan di kolom kiri.
24 Pengurangan (7 – 5) – 4 = (2 – (–1)) – 3 = (23 4− 1 3) − 1 = (4,6 – 3,2) – 0,5 = 7 – (5 – 4) = 2 – (–1 – 3) = 23 4− ( 1 3− 1) = 4,6 – (3,2 – 0,5) = Perkalian (3 × (–2)) × 4 = (23 4× 1 3) × (– 3) = (4 × 2,4) × 0,5 = 3 × (–2 × 4) = 23 4× ( 1 3× (−1)) = 4 × (2,4 × 0,5) = Pembagian (6 ÷ 3) ÷ 2 = (−8 ÷ 4) ÷ (−3) = (2 3÷ 1 1 4) ÷ 4 = 6 ÷ (3 ÷ 2) = −8 ÷ (4 ÷ (−3)) = 2 3÷ (1 1 4÷ 4) =
25 Apakah operasi pengurangan bersifat asosiatif?
Apakah operasi perkalian bersifat asosiatif? Apakah operasi pembagian bersifat asosiatif?
Sama halnya dengan sifat komutatif, sifat asosiatif juga memudahkan kita dalam menghitung hasil penjumlahan dan perkalian. Contohnya, penjumlahan 53 + 86 + 47 + 24 lebih mudah dilakukan dengan menukar tempat dan mengelompokkan suku-suku penjumlahannya menjadi (53 + 47) + (86 + 24) = 100 + 110 = 210.
Begitu juga perkalian 4 × 39 × 25 lebih mudah dihitung dengan (4 × 25) × 39 = 100 × 39 = 3900.
4.6 Unsur Identitas
Dalam matematika, 0 dan 1 adalah bilangan yang istimewa. Diskusikan kasus-kasus berikut ini untuk melihat keistimewaan 0 dan 1.
a. Menjumlahkan suatu bilangan positif atau negatif dengan 0. Contoh: a. 5 + 0 = ....
b. –6 + 0 = .... c. 1235 + 0 = .... Kesimpulan:
b. Mengurangkan suatu bilangan positif atau negatif dengan 0. Contoh: a. 5 – 0 = ....
26 c. 450 – 0 = ....
Kesimpulan:
c. Mengalikan suatu bilangan positif atau negatif dengan 0. Contoh: a. 2 × 0 = ....
b. −3 × 0 = .... c. 1000 × 0 = .... Kesimpulan:
d. Membagi suatu bilangan positif atau negatif dengan 0. Contoh: a. 4 : 0 = ....
b. –3 : 0 = .... c. 120 : 0 = .... Kesimpulan:
e. Membagi 0 dengan suatu bilangan positif atau negatif. Contoh: a. 0 : 12 = ....
b. 0 : (–5) = .... c. 0 : 100 = .... Kesimpulan:
f. Mengalikan suatu bilangan positif atau negatif dengan 1. Contoh: a. 3 × 1 = ....
b. –30 × 1 = .... c. 1000 × 1 = .... Kesimpulan:
27 g. Membagi suatu bilangan positif atau negatif dengan 1.
Contoh: a. 27 : 1 = .... b. –50 : 1 = .... c. 1500 : 1 = .... Kesimpulan:
h. Membagi 1 dengan suatu bilangan positif atau negatif. Contoh: a. 1 : 2 = ....
b. 1 : 4 = .... c. 1 : (–50) = .... Kesimpulan:
Kasus a di atas menunjukkan keistimewaan 0 sebagai unsur identitas penjumlahan. Sedangkan kasus f menunjukkan 1 sebagai unsur identitas perkalian. Hal ini dapat didefinisikan sebagai berikut.
Catatan. Operasi pengurangan dan pembagian tidak memiliki unsur identitas.
Unsur Identitas
0 adalah unsur identitas penjumlahan karena menjumlahkan dengan 0 tidak mengubah hasil penjumlahan. Secara umum ditulis,
𝑝 + 0 = 0 + 𝑝 = 𝑝
1 adalah unsur identitas perkalian karena mengalikan dengan 1 tidak mengubah hasil perkalian. Secara umum ditulis,
28 4.7 Invers
Dalam operasi hitung dikenal istilah invers penjumlahan dan invers perkalian. Untuk memahami makna invers penjumlahan, lengkapi perhitungan berikut ini.
1 + .... = 0, maka invers penjumlahan dari 1 adalah .... 24 + .... = 0, maka invers penjumlahan dari 24 adalah .... –3 + .... = 0, maka invers penjumlahan dari –3 adalah ....
3
5 + .... = 0, maka invers penjumlahan dari 3
5 adalah .... −1
2 + .... = 0, maka invers penjumlahan dari − 1
2 adalah ....
Invers penjumlahan dari suatu bilangan adalah lawan dari bilangan itu. Apabila suatu bilangan dijumlahkan dengan invers
penjumlahannya maka hasilnya 0. Secara umum ditulis, 𝑝 + (−𝑝) = 0.
Untuk memahami makna invers perkalian, lengkapi perhitungan berikut ini.
2 × .... = 1, maka invers perkalian dari 2 adalah .... −5 × .... = 1, maka invers perkalian dari −5 adalah .... 3
4× .... = 1, maka invers perkalian dari 3
4 adalah .... −1
2× .... = 1, maka invers perkalian dari − 1
2 adalah .... 3,5 .... = 1, maka invers perkalian dari 3,5 adalah ....
29 Invers perkalian dari suatu bilangan adalah kebalikan (reciprocal) dari bilangan tersebut. Apabila suatu bilangan dikalikan dengan kebalikannya maka hasilnya 1. Secara umum ditulis, 𝑝 ×1
𝑝= 1.
4.8 Sifat Distributif
Pada operasi hitung berlaku sifat distributif (penyebaran), yaitu p × (q + r) = p × q + p × r dan
(p + q) × r = p × r + q × r
Sifat distributif memudahkan kita dalam melakukan operasi hitung. Contohnya, 25 × 42 dapat diselesaikan sebagai berikut.
25 × 42 = 25 × (40 + 2)
= (25 × 40) + (25 × 2) = 1000 + 50
= 1050
Contoh lain, 16 × 5 dapat diselesaikan sebagai berikut. 36 × 5 = (30 + 6) × 5
= (30 × 5) + (6 × 5) = 150 + 30
30 4.9 Sifat Ketertambahan.
Misalkan p, q, dan r adalah bilangan real. Jika p = q, maka p + r = q + r. Sifat ini dinamakan sifat ketertambahan, yaitu
menambahkan bilangan yang sama pada kedua ruas penjumlahan tidak mengubah hasil penjumlahan tersebut.
Sifat ketertambahan digunakan dalam menyelesaikan suatu persamaan yang memuat operasi penjumlahan.
Contoh:
1. Tentukan nilai m yang memenuhi 3 + m = 12.
Soal ini diselesaikan dengan menerapkan sifat ketertambahan, yaitu kedua ruas ditambah dengan –3 sebagai berikut.
3 + m + (–3) = 12 + (–3), m = 9.
2. Tentukan nilai k yang memenuhi.
a) k – 3 = 8 k = 8 + ... k = .... b) 2k + 4 = 10 + k 2k – k = .... – .... k = ....
31 4.10 Sifat Ketergandaan
Misalkan p, q, dan r adalah bilangan real. Jika p = q, maka p×r = q×r. Sifat ini dinamakan sifat ketergandaan, yaitu mengalikan bilangan yang sama pada kedua ruas perkalian tidak mengubah hasil perkalian tersebut.
Sifat ketergandaan diterapkan dalam menyelesaikan suatu persamaan operasi perkalian.
Contoh:
1. Tentukan nilai m yang memenuhi 8m = 24.
Soal ini diselesaikan dengan menggunakan sifat ketergandaan, yaitu kedua ruas dikalikan dengan invers dari 8 yaitu 1
8 8m × 1 8 = 24 × 1 8 , m = 3.
2. Tentukan nilai p yang memenuhi a) 9p – 3 = 15 9p = ... p = ... b) 10 – 3p = 4p + 3 4.11 Sifat Kanselasi
Pada operasi penjumlahan dan perkalian bilangan real juga berlaku sifat kanselasi. Misalkan p, q, dan r adalah bilangan real. Sifat kanselasi pada penjumlahan yaitu jika p + r = q + r, maka p = q. Sifat
32 kanselasi pada perkalian yaitu jika p × r = q × r dan r ≠ 0, maka p = q.
Contoh:
1. Tentukan nilai m yang memenuhi 125 + m = 175.
Soal ini dapat diselesaikan dengan menerapkan sifat ketertambahan, namun juga dapat diselesaikan dengan menerapkan sifat kanselasi sebagai berikut.
125 + m = 125 + 50, artinya m = 50.
2. Tentukan nilai t yang memenuhi 13t = 39.
Soal ini dapat diselesaikan dengan menerapkan sifat ketergandaan yaitu membagi kedua ruas dengan 13, namun bisa juga diselesaikan dengan menerapkan sifat kanselasi sebagai berikut.
13 × t = 13 × 3, artinya t = 3.
Soal Latihan
1. Lingkari Benar (B) atau Salah (S) pada pernyataan-pernyataan berikut ini. Apabila salah, tuliskan jawaban yang benarnya.
a. B – S Perkalian bilangan cacah bersifat asosiatif. b. B – S Pengurangan bilangan asli bersifat tertutup. c. B – S Invers penjumlahan dari 10 adalah 1
10 d. B – S Invers perkalian dari 25 adalah –25
33 e. B – S Operasi-operasi yang memenuhi sifat komutatif adalah penjumlahan, pengurangan dan perkalian bilangan rasional.
2. Pada soal berikut ini, terapkan sifat komutatif dan asosiatif dalam menghitung hasilnya.
a. 47 + 58 + 12 b. 34 + 23 + 46 + 17 c. 4 × 3,4 × 5 3. Tentukan nilai k. a. 5 – k = 16 – 2k b. 4k – 8 = k + 19 c. 3,5 + 2k = 7,7
4. Sifat apakah yang ditunjukkan berikut ini sehingga ruas kiri
dapat dinyatakan menjadi seperti yang tertera pada ruas kanan? a. (a + b) + ((−c) + c) = a + b
i. ((−c) × a) + ((−c) × b) = (−c) (a + b) j. (−a) + (−b + b) + c = (−a) + c
34
5. ATURAN PENJUMLAHAN, PENGURANGAN,
PERKALIAN DAN PEMBAGIAN BILANGAN
BULAT
Tujuan Pembelajaran:
Mahasiswa mampu menyelesaikan operasi penjumlahan, pengurangan, perkalian dan pembagian bilangan.
Operasi penjumlahan, pengurangan, perkalian, dan pembagian bilangan bulat merupakan operasi hitung yang biasa digunakan dalam kehidupan sehari-hari. Prosedur melakukan operasi hitung telah diajarkan sejak sekolah dasar dan selalu digunakan baik dalam ruang belajar maupun di luar kelas. Aturan-aturan operasi hitungpun telah dimaklumi secara luas, misalnya perkalian dua bilangan bulat negatif menghasilkan bilangan positif, perkalian dengan 0 menghasilkan 0, dan lain-lain. Pada bab ini akan dibahas pembuktian aturan-aturan tersebut dimulai dari aturan penjumlahan dan pengurangan bilangan bulat.
5.1 Aturan Penjumlahan dan Pengurangan Bilangan Bulat
Berikut akan dibahas pembuktian tiga aturan penting dalam penjumlahan dan pengurangan bilangan bulat.
1. (−𝑝) + (−𝑞) = −(𝑝 + 𝑞)
Bukti
(−𝑝) + (−𝑞) = (−𝑝) + (−𝑞) + 0
35 = (𝑝 + (−𝑝)) + (𝑞 + (−𝑞)) + (−(𝑝 + 𝑞)) = 0 + 0 + −(𝑝 + 𝑞) = −(𝑝 + 𝑞) Contoh: a. −2 + (−3) = −(2 + 3) = −5 b. −4 + (−2) = −6 2. 𝑝 + (−𝑞) = 𝑝 − 𝑞 Bukti 𝑝 + (−𝑞) = 𝑝 + (−𝑞) + 0 = 𝑝 + (−𝑞) + 𝑞 − 𝑞 = 𝑝 + ((−𝑞) + 𝑞) − 𝑞 = 𝑝 + 0 − 𝑞 = 𝑝 − 𝑞 Contoh: a. 3 + (−2) = 3 − 2 = 1 b. 5 + (−1) = 4 3. 𝑝 − (−𝑞) = 𝑝 + 𝑞 Bukti
Pada no.2 telah dibuktikan bahwa 𝑝 − 𝑞 = 𝑝 + (−𝑞), maka 𝑝 − (−𝑞) = 𝑝 + (−(−𝑞)) = 𝑝 + (−(−𝑞)) + 0 = 𝑝 + (−(−𝑞)) + 𝑞 + (−𝑞) = 𝑝 + 𝑞 + (−(−𝑞)) + (−𝑞) = 𝑝 + 𝑞 + 0 = 𝑝 + 𝑞
36 Contoh: a. 2 − (−5) = 2 + 5 = 7
b. 3 − (−1) = 4
Soal Latihan
Jawablah soal-soal berikut. 1. –4 + (–5) = 2. 4 + (–1) = 3. –2 + (–6) = 4. 3 – (–2) = 5. –5 – (–1) =
5.2 Aturan Perkalian Bilangan Bulat
Berikut akan dibahas tiga aturan penting dalam perkalian bilangan bulat dimulai dari aturan yang pertama yaitu perkalian dengan 0 menghasilkan 0. 1. 𝑝. 0 = 0 Bukti 𝑝. 0 = 𝑝. 0 + 0 = 𝑝. 0 + 𝑝𝑞 + (−(𝑝𝑞)) = 𝑝(0 + 𝑞) + (−(𝑝𝑞)) = 𝑝𝑞 + (−(𝑝𝑞)) = 0
37 2. 𝑝(−𝑞) = −(𝑝𝑞) dan (−𝑝)𝑞 = −(𝑝𝑞)
Aturan ini menyebutkan bahwa bilangan positif dikali bilangan negatif, hasilnya adalah bilangan negatif.
Bukti
Pertama akan ditunjukkan bahwa 𝑝(−𝑞) = −(𝑝𝑞) 𝑝(−𝑞) = 𝑝(−𝑞) + 0 = 𝑝(−𝑞) + 𝑝𝑞 + (−(𝑝𝑞)) = 𝑝(−𝑞 + 𝑞) + (−(𝑝𝑞)) = 𝑝(0) + (−(𝑝𝑞)) = 0 + (−(𝑝𝑞)) = −(𝑝𝑞)
Selanjutnya akan ditunjukkan bahwa (−𝑝)𝑞 = −(𝑝𝑞) (−𝑝)𝑞 = (−𝑝)𝑞 + 0 = (−𝑝)𝑞 + 𝑝𝑞 + (−(𝑝𝑞)) = (−𝑝 + 𝑝)𝑞 + (−(𝑝𝑞)) = (0)𝑞 + (−(𝑝𝑞)) = 0 + (−(𝑝𝑞)) = −(𝑝𝑞) 3. (−𝑝)(−𝑞) = 𝑝𝑞
Aturan ini menyebutkan bahwa bilangan negatif dikali dengan bilangan negatif, hasilnya adalah bilangan positif.
Bukti
(−𝑝)(−𝑞) = (−𝑝)(−𝑞) + 0
38
= ((−𝑝)(−𝑞) + (−(𝑝𝑞))) + 𝑝𝑞
Pada aturan no.2 telah dibuktikan bahwa−(𝑝𝑞) = (−𝑝)𝑞, maka = ((−𝑝)(−𝑞) + ((−𝑝)𝑞)) + 𝑝𝑞 = (−𝑝)(−𝑞 + 𝑞) + 𝑝𝑞 = (−𝑝)(0) + 𝑝𝑞 = 0 + 𝑝𝑞 = 𝑝𝑞 Soal Latihan
Tentukan hasil perkalian bilangan-bilangan bulat berikut ini. 1. 1000 × 0 = …… 2. 0 × (–250) = …… 3. 4 × (–3) = …… 4. –2 × 6 = …… 5. –7 × (–2) = ……… 6. Jika 50 × a = 0, maka a = …….
5.3 Aturan Pembagian Bilangan Bulat
Ingat kembali definisi pembagian bilangan bulat, yaitu 𝑝 ÷ 𝑞 = 𝑟 ⟺ 𝑝 = 𝑞𝑟, dimana 𝑞 ≠ 0. Hal ini menunjukkan bahwa operasi pembagian berkaitan erat dengan operasi perkalian.
39 Dari aturan perkalian p(–q) = –(pq), maka menurut definisi pembagian:
–(pq) ÷ p = –q –(pq) ÷ (–q) = p
Begitu juga untuk (–p)q = –(pq), maka menurut definisi pembagian: –(pq) ÷ (–p) = q
–(pq) ÷ q = –p
Demikian pula untuk (–p)( –q) = pq, maka: pq ÷ (–p) = –q dan
pq ÷ (–q) = –p
Dari turunan di atas dapat disimpulkan:
1. Bilangan negatif dibagi bilangan positif hasilnya bilangan negatif.
2. Bilangan positif dibagi bilangan negatif hasilnya bilangan negatif.
3. Bilangan negatif dibagi bilangan negatif hasilnya bilangan positif.
Berikut akan dijabarkan aturan-aturan pembagian bilangan bulat.
1. p ÷ 1 = p.
Bukti
Mencari hasil pembagian p ÷ 1 = …., artinya mencari bilangan yang memenuhi p = 1 × …. Dari sifat identitas perkalian
40 diketahui bilangan yang memenuhi adalah p yaitu p = 1 × p. Jadi, p ÷ 1 = p. Disimpulkan bahwa semua bilangan bulat dibagi 1 hasilnya adalah bilangan bulat itu sendiri.
Contoh: a. 5 ÷ 1 = 5 b. –7 ÷ 1 = –7 c. 0 ÷ 1 = 0 d. 100 ÷ 1 = 100 e. –2500 ÷ 1 = –2500 2. p ÷ p = 1 Bukti
Sama seperti pembuktian no.1, mencari hasil pembagian p ÷ p adalah mencari bilangan yang memenuhi p = p × …. Dari sifat identitas perkalian diketahui bilangan yang memenuhi adalah 1 karena p = p × 1.
Disimpulkan bahwa setiap bilangan bulat dibagi dengan dirinya sendiri hasilnya adalah 1.
Contoh: a. 2 ÷ 2 = 1 b. –4 ÷ –4 = 1 c. 1000 ÷ 1000 = 1
41 3. p × (1 ÷ p) = 1
Bukti
Pembuktiaan dilakukan dengan mencari hasil perkalian p × (1 ÷ p) = …. Dari definisi invers perkalian diketahui bahwa
(1 ÷ p) adalah invers perkalian dari p. Telah diketahui pula bahwa
hasil perkalian suatu bilangan dengan inversnya adalah 1. Jadi, p × (1 ÷ p) = 1. Contoh: a. 6 × (1 ÷ 6) = 1 b. –5 × (1 ÷ (–5)) = 1 c. –30 × (1 ÷ (–30)) = 1 4. p ÷ (p ÷ q) = q Bukti:
Untuk mencari hasil pembagian p ÷ (p ÷ q) = …, terlebih dahulu dimisalkan (p ÷ q) = k, maka dari definisi pembagian dapat ditulis p = q × k, atau p = k × q. Substitusikan kembali nilai k sehingga didapatkan p = (p ÷ q) × q.
Menurut definisi pembagian, p = (p ÷ q) × q artinya p÷(p÷q) = q.
Contoh:
a. 7 ÷ (7 ÷ 3) = 3 b. –2 ÷ ((–2) ÷ 5) = 5 c. –3 ÷ ((–3) ÷ (–4)) = –4
42 5. p ÷ q = p × (1 ÷ q) Bukti p ÷ q = (p ÷ q) × 1 = (p ÷ q) × [q × (1 ÷ q)] = [(p ÷ q) × q] × (1 ÷ q)
Pada aturan 4 telah ditunjukkan bahwa p ÷ (p ÷ q) = q. Berdasarkan definisi pembagian, ini berarti p = (p ÷ q) × q, atau (p ÷ q) × q = p.
Jadi, [(p ÷ q) × q] × (1 ÷ q) = p × (1 ÷ q), maka terbukti bahwa p ÷ q = p × (1 ÷ q). Contoh: a. 2 ÷ 3 = 2 × (1 ÷ 3) b. 4 ÷ (–7) = 4 × (1 ÷ –7) 6. (1 ÷ p) × (1 ÷ q) = 1 ÷ pq Bukti (1 ÷ p) × (1 ÷ q) = 1 × (1 ÷ p) × (1 ÷ q) = (pq ÷ pq) × (1 ÷ p) × (1 ÷ q) (aturan 2) = [pq×(1 ÷ pq)]×(1 ÷ p) × (1 ÷ q) (aturan 4) = [p × (1 ÷ p)] × [q × (1 ÷ q)] × (1 ÷ pq) = 1 × 1 × (1 ÷ ab) (aturan 3) = 1 ÷ pq Contoh: a. (1 ÷ 2) × (1 ÷ 3) = 1 ÷ (2.3) = 1 ÷ 6
43 b. (1 ÷ (–4)) × (1 ÷ 5) = 1 ÷ (–4.5) = 1 ÷ (–20) c. (1 ÷ (–3)) × (1 ÷ (–6)) = 1 ÷ ((–3)( –6)) = 1 ÷ 18 7. (p ÷ q) × (r ÷ s) = pr ÷ qs Bukti: (p ÷ q) × (r ÷ s) = [p × (1 ÷ q)] × [r × (1 ÷ s)] (aturan 5) = pr × [(1 ÷ q) × (1 ÷ s)] = pr × (1 ÷ qs) (aturan 6) = pr ÷ qs (aturan 4) Catatan:
Perkalian (p ÷ q) × (r ÷ s) = pr ÷ qs dapat pula ditulis dalam bentuk pecahan sebagai berikut. 𝑝
𝑞 × 𝑟 𝑠 =
𝑝𝑟 𝑞𝑠
Dapat disimpulkan bahwa cara menghitung perkalian dua pecahan adalah pembilang kali pembilang dan penyebut kali penyebut. Contoh: a. (2 ÷ 5) × (3 ÷ 4) =2 5 × 3 4= 2 × 3 5 × 4= 6 20= 3 10 b. (1 ÷ (–5)) × (6 ÷ 7) = 1 −5 × 6 7 = 1 × 6 −5 × 7= 6 −35= − 6 35 8. (p ÷ q) + (r ÷ q) = (p + q) ÷ r Bukti (p ÷ q) + (r ÷ q) = [p × (1 ÷ q)] + [r × (1 ÷ q)] (aturan 5) = (p + r) × (1 ÷ q) = (p + r) ÷ q (aturan 5)
44 Catatan:
Penjumlahan (p ÷ q) + (r ÷ q) = (p + r) ÷ q dapat pula ditulis dalam bentuk pecahan 𝑝
𝑞+ 𝑟 𝑞=
𝑝 + 𝑟 𝑞
Dapat disimpulkan bahwa cara menjumlahkan dua pecahan berpenyebut sama adalah dengan menjumlahkan kedua pembilangnya, sedangkan penyebutnya tetap.
Contoh: a. (4 ÷ 5) + (7 ÷ 5) = 4 5+ 7 5 = 4 + 7 5 = 11 5 = 2 1 5 b. (3 ÷ 4) + ((–1) ÷ 4) = 3 4+ −1 4 = 3 +(−1) 4 = 3−1 4 = 2 4 = 1 2 9. (p ÷ q) ÷ (r ÷ s) = ps ÷ qr Bukti
Dengan menggunakan bentuk pecahan, (p ÷ q) ÷ (r ÷ s) dapat dijabarkan sebagai berikut.
(p ÷ q) ÷ (r ÷ s) = 𝑝 𝑞 𝑟 𝑠 = 𝑝 𝑞 𝑟 𝑠 × 1 = 𝑝 𝑞 𝑟 𝑠 × 𝑠 𝑟 𝑠 𝑟 = 𝑝 𝑞 × 𝑠 𝑟 1 = 𝑝 𝑞 × 𝑠 𝑟
45
= 𝑝𝑠
𝑞𝑟 Jadi (p ÷ q) ÷ (r ÷ s) = ps ÷ qr.
Catatan: Dapat disimpulkan pembagian dua pecahan dapat ditulis sebagai perkalian, dimana suku kedua dibalik.
Contoh a. (3 ÷ 2) ÷ (4 ÷ 5) =3 2÷ 4 5 = 3 ×5 2 ×4= 15 8 = 1 7 8 b. (–1 ÷ 3) ÷ (2 ÷ (–7)) =−1 3 ÷ 2 −7= −1 ×(−7) 3 ×2 = 7 6 = 1 1 6 Soal Latihan
Selesaikan soal-soal pembagian berikut ini. 1. –5 ÷ (2 ÷ (–4)) 2. 5 ÷ ((–2) ÷ (–4)) 3. ((–5) ÷2) ÷ (–4) 4. (–4 ÷ 3) × (2 ÷ 8) 5. (1 ÷ (–6)) × (1÷2) 6. (9 ÷ (–2)) ÷ (3÷4)
46
6. URUTAN BILANGAN BULAT
Tujuan Pembelajaran
Mahasiswa mampu menentukan urutan bilangan bulat.
Urutan bilangan bulat merupakan relasi yang menggambarkan nilai suatu bilangan bulat terhadap bilangan bulat lainnya. Urutan bilangan bulat dapat digambarkan pada garis bilangan sebagai berikut.
Pada garis bilangan, apabila suatu bilangan 𝑝 terletak di sebelah kanan bilangan 𝑞, maka 𝑝 lebih besar nilainya daripada 𝑞. Namun apabila 𝑝 berada di sebelah kiri 𝑞, maka 𝑝 lebih kecil nilainya daripada 𝑞. Contohnya, –2 lebih besar dari –3, tetapi –2 lebih kecil dari 0. Simbol untuk menyatakan 𝑝 lebih besar dari 𝑞 adalah 𝑝 > 𝑞, dan simbol untuk menyatakan 𝑝 lebih kecil dari 𝑞 adalah 𝑝 < 𝑞.
Pada relasi urutan bilangan bulat berlaku sifat transitif, yaitu jika 𝑝 < 𝑞 dan 𝑞 < 𝑟, maka 𝑝 < 𝑟. Sebagai contoh, −1 < 4 dan 4 < 5, maka −1 < 5.
Perlu diingat, 5 > 4 sama artinya dengan 4 < 5. Begitu juga –2 < 0 sama artinya dengan 0 > –2.
Secara umum ditulis, (𝑝 > 𝑞) ⟺ (𝑞 < 𝑝) dan (𝑝 < 𝑞) ⟺ (𝑞 > 𝑝).
-2 -1 0 1 2 3 4 5
47 Definisi urutan bilangan bulat.
Untuk bilangan bulat 𝑝 dan 𝑞, berlaku 𝑝 < 𝑞 jika dan hanya jika terdapat sebuah bilangan bulat positif 𝑟 sehingga 𝑝 + 𝑟 = 𝑞.
Contoh:
a. 2 < 5 artinya terdapat suatu bilangan bulat positif yaitu … sehingga 2 + … = 5.
b. –3 < –1 artinya terdapat suatu bilangan bulat positif yaitu … sehingga –3 + … = –1.
c. –4 < 2 artinya terdapat suatu bilangan bulat positif yaitu … sehingga –4 + … = 2.
Ingat kembali aturan pada perkalian bilangan positif dan negatif a. Jika 𝑝 > 0 dan 𝑞 > 0 maka 𝑝𝑞 > 0
b. Jika 𝑝 > 0 dan 𝑞 < 0 maka 𝑝𝑞 < 0 c. Jika 𝑝 < 0 dan 𝑞 < 0 maka 𝑝𝑞 > 0
Poin a, b dan c di atas menyatakan bahwa perkalian bilangan positif dengan bilangan positif menghasilkan bilangan positif; perkalian bilangan positif dengan bilangan negatif menghasilkan bilangan negatif; dan perkalian bilangan negatif dengan bilangan negatif menghasilkan bilangan positif.
Ketiga poin di atas dapat juga dilihat sebagai berikut. a. Untuk 𝑝𝑞 > 0, jika 𝑝 > 0 maka 𝑞 > 0.
Begitu juga, jika 𝑞 > 0 maka 𝑝 > 0. b. Untuk 𝑝𝑞 > 0, jika 𝑝 < 0 maka 𝑞 < 0.
48 c. Untuk 𝑝𝑞 < 0, jika 𝑝 > 0 maka 𝑞 < 0.
Begitu juga, jika 𝑞 > 0 maka 𝑝 < 0.
Berikut ini akan dibahas beberapa sifat dan aturan yang berlaku pada relasi urutan bilangan bulat.
1. Sifat ketertambahan pada ketaksamaan. Yaitu jika 𝑝 < 𝑞, maka 𝑝 + 𝑐 < 𝑞 + 𝑐.
Bukti
𝑝 < 𝑞 artinya terdapat suatu bilangan bulat positif 𝑟 sehingga 𝑝 + 𝑟 = 𝑞.
Menambahkan kedua ruas dengan suatu bilangan bulat 𝑐 diperoleh (𝑝 + 𝑟) + 𝑐 = 𝑞 + 𝑐. atau (𝑝 + 𝑐) + 𝑟 = 𝑞 + 𝑐. Jadi, (𝑝 + 𝑐) < (𝑞 + 𝑐). Contoh: a. 1 < 4, maka (1 + 2) < (4 + 2) yaitu 3 < 6. b. –2 < 5, maka (–2 + 3) < (5 + 3) yaitu 1 < 8. c. –3 < 6, maka (–3 + (–2)) < (6 + (–2)) yaitu –5 < 4.
2. Sifat kanselasi pada ketaksamaan. Yaitu jika (𝑝 + 𝑐) < (𝑞 + 𝑐) maka 𝑝 < 𝑞.
Bukti
(𝑝 + 𝑐) < (𝑞 + 𝑐) berarti terdapat suatu bilangan bulat positif 𝑟 sehingga (𝑝 + 𝑐) + 𝑟 = 𝑞 + 𝑐.
49 Apabila kedua ruas ditambahkan dengan – 𝑐 maka diperoleh (𝑝 + 𝑐) + 𝑟 + (−𝑐) = 𝑞 + 𝑐 + (−𝑐). Sehingga didapatkan 𝑝 + 𝑟 = 𝑞. Ini artinya 𝑝 < 𝑞.
3. Misalkan 𝑝, 𝑞 dan 𝑟 adalah bilangan bulat.
a. Untuk 𝑟 > 0, berlaku 𝑝 < 𝑞 jika dan hanya jika 𝑝𝑟 < 𝑞𝑟. b. Untuk 𝑟 < 0, berlaku 𝑝 < 𝑞 jika dan hanya jika 𝑝𝑟 > 𝑞𝑟.
Aturan 3a mengatakan bahwa pada ketaksamaan 𝑝 < 𝑞, apabila kedua ruas dikalikan dengan suatu bilangan bulat positif 𝑟, maka 𝑝𝑟 < 𝑞𝑟. Begitu juga sebaliknya, pada ketaksamaan 𝑝𝑟 < 𝑞𝑟, apabila 𝑟 > 0, maka 𝑝 < 𝑞.
Sebagai contoh, 3 < 5. Bila kedua ruas dikalikan dengan 2, maka diperoleh (3 × 2) < (5 × 2) yaitu 6 < 10.
Aturan 3b mengatakan bahwa pada ketaksamaan 𝑝 < 𝑞, apabila kedua ruas dikalikan dengan suatu bilangan bulat negatif 𝑟, maka 𝑝𝑟 > 𝑞𝑟. Begitu pula sebaliknya, pada ketaksamaan 𝑝𝑟 > 𝑞𝑟, apabila 𝑟 < 0, maka 𝑝 < 𝑞.
Sebagai contoh, 3 < 5. Bila kedua ruas dikalikan dengan –2, maka diperoleh (3 × (−2)) > (5 × (−2)) yaitu −6 > −10.
Dengan kata lain, apabila kedua ruas ketaksamaan dikali dengan suatu bilangan positif, maka tanda ketaksamaannya tetap. Namun apabila kedua ruas ketaksamaan dikali dengan bilangan negatif, maka tanda ketaksamaannya berubah.
50 Berikut akan diberikan pembuktian untuk aturan 3a dan 3b.
3a. Untuk bilangan bulat 𝑝, 𝑞 dan 𝑟. Apabila 𝑟 > 0, berlaku 𝑝 < 𝑞 jika dan hanya jika 𝑝𝑟 < 𝑞𝑟.
Pernyataan di atas memuat relasi ‘jika dan hanya jika’, artinya berlaku dua arah yaitu:
1) jika 𝑝 < 𝑞 maka 𝑝𝑟 < 𝑞𝑟, dan sebaliknya 2) jika 𝑝𝑟 < 𝑞𝑟 maka 𝑝 < 𝑞.
Oleh karena itu, pembuktiannya ada dua arah.
Bukti
1) Akan ditunjukkan bahwa jika 𝑝 < 𝑞 maka 𝑝𝑟 < 𝑞𝑟.
𝑝 < 𝑞 berarti terdapat bilangan bulat positif 𝑘 sehingga 𝑝 + 𝑘 = 𝑞. Apabila kedua ruas dikalikan dengan 𝑟, maka
diperoleh:
(𝑝 + 𝑘) × 𝑟 = 𝑞 × 𝑟 (𝑝𝑟) + (𝑘𝑟) = 𝑞𝑟
(𝑘𝑟) bernilai positif, maka berdasarkan definisi urutan bilangan bulat disimpulkan bahwa 𝑝𝑟 < 𝑞𝑟.
2) Akan ditunjukkan bahwa jika 𝑝𝑟 < 𝑞𝑟 maka < 𝑞.
Pada ketaksamaan 𝑝𝑟 < 𝑞𝑟, bila kedua ruas ditambah dengan (–𝑞𝑟), maka diperoleh:
𝑝𝑟 + (−𝑞𝑟) < 𝑞𝑟 + (−𝑞𝑟) (𝑝 + (−𝑞)) × 𝑟 < 0
Karena 𝑟 > 0, maka (𝑝 + (−𝑞)) < 0
51 𝑝 + (−𝑞) + 𝑞 < 0 + 𝑞
Jadi, 𝑝 < 𝑞.
3b. Untuk bilangan bulat 𝑝, 𝑞 dan 𝑟. Apabila 𝑟 < 0, berlaku 𝑝 < 𝑞 jika dan hanya jika 𝑝𝑟 > 𝑞𝑟.
Pernyataan ini berarti:
1) jika 𝑝 < 𝑞 maka 𝑝𝑟 > 𝑞𝑟, dan sebaliknya 2) jika 𝑝𝑟 > 𝑞𝑟 maka 𝑝 < 𝑞.
Bukti
1) Akan ditunjukkan bahwa jika 𝑝 < 𝑞 maka 𝑝𝑟 > 𝑞𝑟.
𝑝 < 𝑞 berarti berarti terdapat bilangan bulat positif 𝑘 sehingga 𝑝 + 𝑘 = 𝑞.
Tambahkan kedua ruas dengan – 𝑘, diperoleh: 𝑝 = 𝑞 + (−𝑘)
Mengalikan kedua ruas dengan 𝑟, diperoleh: 𝑝𝑟 = (𝑞 + (−𝑘))𝑟
𝑝𝑟 = 𝑞𝑟 + (−𝑘𝑟) atau 𝑞𝑟 + (−𝑘𝑟) = 𝑝𝑟
Karena (−𝑘𝑟) > 0, maka menurut definisi urutan bilangan bulat disimpulkan bahwa 𝑞𝑟 < 𝑝𝑟, atau 𝑝𝑟 > 𝑞𝑟.
2) Akan ditunjukkan bahwa 𝑝𝑟 > 𝑞𝑟 maka 𝑝 < 𝑞. 𝑝𝑟 > 𝑞𝑟 𝑝𝑟 + (−𝑞𝑟) > 𝑞𝑟 + (−𝑞𝑟) (𝑝 + (−𝑞)) × 𝑟 > 0 Karena 𝑟 < 0 maka (𝑝 + (−𝑞)) < 0 𝑝 + (−𝑞) + 𝑞 < 0 + 𝑞 Jadi, 𝑝 < 𝑞.
52 Soal Latihan
Untuk soal nomor 1 sampai 6, pilihlah pilihan jawaban yang paling benar. Soal nomor 1 sampai 4 dikutip dari buku Herry Sukarman yang berjudul Teori Bilangan.
1. Jika p, q, dan r bilangan bulat dan p > q, maka …. a. p × r > q × r
b. p × r < q × r c. p – r > q – r
2. Jika a × (–c) < b × (–c) maka a < b. Dari pernyataan ini dapat disimpulkan bahwa
a. c adalah bilangan bulat tidak nol b. c adalah bilangan bulat positif c. c adalah bilangan bulat negatif
3. Jika (p + q) × r < 0 dan (p + q) > 0, maka ….. a. p > q
b. r > 0 c. r < 0
4. Jika p, q, r, dan s bilangan bulat dengan p > q dan r > s, maka pernyataan yang benar adalah …..
a. p × r > q × r b. p + r > q + r c. p – q > r – s
53 Soal nomor 5 dan 6 berikut ini dikutip dari laporan penelitian Zachary Scott McIntyre (2005).
Untuk soal 7 dan 8, uraikan jawaban Anda. 7. Jika 𝑎 > 0, kapankah 𝑎𝑏 bernilai negatif?
8. Jika diketahui (𝑝 + 𝑞) (𝑝𝑞) > 0 dan 𝑝𝑞 < 0, maka apa yang dapat disimpulkan tentang 𝑝 dan 𝑞?
5. Diketahui x adalah suatu bilangan Riil. Apabila x < 5, maka manakah yang benar dari tiga pilihan jawaban berikut ini?
a. x + 1 = 5 b. x + 1 < 5 c. x + 1 < 6
6. Apabila diketahui x adalah bilangan Riil yang nilainya lebih besar dari 7, maka nilai 2x + 1 ….
a. sama dengan 17 b. lebih besar dari 15 c. lebih besar dari 16
54
7. KETERBAGIAN BILANGAN BULAT
Tujuan Pembelajaran
Mahasiswa mampu menentukan keterbagian suatu bilangan bulat.
Konsep keterbagian berkaitan erat dengan konsep faktor dan kelipatan. Pada bab ini akan dibahas tentang keterbagian bilangan bulat dan teorema-teorema yang berlaku pada keterbagian bilangan bulat.
Definisi Keterbagian
Untuk bilangan bulat 𝑝 dan 𝑞, 𝑝 habis membagi 𝑞 (ditulis 𝑝|𝑞) jika dan hanya jika terdapat tepat satu bilangan bulat 𝑘 sehingga 𝑝𝑘 = 𝑞.
Contoh:
3|18 karena terdapat tepat satu bilangan bulat yaitu 6 sehingga 3×6 =18.
3∤20 (dibaca: 3 tidak habis membagi 20) karena tidak terdapat bilangan bulat 𝑘 yang memenuhi 3 × 𝑘 = 20.
4|32 karena terdapat tepat satu bilangan bulat yaitu 8 sehingga 4×8 =32.
4∤25 karena tidak terdapat bilangan bulat 𝑘 yang memenuhi 4 × 𝑘 = 25.
Sebagaimana dapat dilihat dari contoh di atas, jika 𝑝|𝑞 maka 𝑝 adalah faktor dari 𝑞; dan 𝑞 adalah kelipatan dari 𝑝.
55 Dari yang berikut ini, manakah yang benar?
a. 77|7 b. 7|77 c. 24|24 d. 0|24 e. 24|0
Berikut akan dibahas beberapa teorema yang berlaku pada keterbagian bilangan bulat.
1. Jika 𝑝|𝑞 dan 𝑞|𝑟, maka 𝑝|𝑟.
Bukti
𝑝|𝑞 berarti terdapat satu bilangan bulat 𝑘 sehingga 𝑝𝑘 = 𝑞. Begitu juga 𝑞|𝑟 berarti terdapat satu bilangan bulat 𝑚 sehingga 𝑞𝑚 = 𝑟. Dengan mensubstitusikan 𝑝𝑘 = 𝑞 ke 𝑞𝑚 = 𝑟 diperoleh 𝑝𝑘𝑚 = 𝑟. Atau ditulis 𝑝(𝑘𝑚) = 𝑟. Karena 𝑘𝑚 adalah bilangan bulat, maka berdasarkan definisi keterbagian dapat disimpulkan bahwa 𝑝|𝑟.
Contoh:
a. Jika 3|6 dan 6|24 maka 3|24. b. Jika (–2)|4 dan 4|8 maka (–2)|8.
c. Jika 5|(–10) dan (–10)|250 maka 5|250.
2. Jika 𝑝|𝑞 dan 𝑝|𝑟 maka 𝑝|(𝑞 + 𝑟).
56 𝑝|𝑞 berarti terdapat suatu bilangan 𝑚 sehingga 𝑝𝑚 = 𝑞. Begitu juga 𝑝|𝑟 berarti terdapat suatu bilangan 𝑛 sehingga 𝑝𝑛 = 𝑟. Jika dijumlahkan, 𝑝𝑚 + 𝑝𝑛 = 𝑞 + 𝑟
𝑝(𝑚 + 𝑛) = 𝑞 + 𝑟
(𝑚 + 𝑛) adalah suatu bilangan bulat, maka dari definisi keterbagian dapat disimpulkan bahwa 𝑝|(𝑞 + 𝑟).
Contoh:
a. Jika 4|12 dan 4|16 maka 4|(12 + 16) yaitu 4|28. b. Jika 2|(–6) dan (–6)|18 maka 2|(–6+18) yaitu 2|12. c. Jika (–3)| (–9) dan (–9)|27 maka (–3)|( (–9 + 27) yaitu (–
3)|18.
3. Jika 𝑝|𝑞 maka 𝑝|𝑟𝑞 untuk sembarang bilangan bulat 𝑟. Dengan kata lain, jika 𝑝|𝑞, maka 𝑝 membagi semua kelipatan 𝑞.
Bukti
𝑝|𝑞 berarti terdapat bilangan bulat 𝑘 sehingga 𝑝𝑘 = 𝑞. Apabila kedua ruas dikali dengan suatu bilangan bulat 𝑟, maka diperoleh 𝑝𝑘𝑟 = 𝑞𝑟. Atau dapat ditulis 𝑝(𝑘𝑟) = 𝑞𝑟. Menurut definisi keterbagian, dapat disimpulkan bahwa 𝑝|𝑞𝑟.
Contoh:
Diketahui 5|30. Maka 5| (30 × (–2)) 5| (30 × 0) 5| (30 × 4)
57 4. Jika 𝑝|𝑞 dan 𝑞|𝑝 maka 𝑝 = 𝑞 atau 𝑝 = −𝑞.
Bukti
𝑝|𝑞 berarti terdapat bilangan bulat 𝑘 sehingga 𝑝𝑘 = 𝑞. Begitu juga, 𝑞|𝑝 berarti terdapat bilangan bulat 𝑙 sehingga 𝑞𝑙 = 𝑝. Dengan mensubstitusikan 𝑞 = 𝑝𝑘 ke 𝑞𝑙 = 𝑝, diperoleh 𝑝𝑘𝑙 = 𝑝. Menurut aturan perkalian, haruslah 𝑘𝑙 = 1. Hal ini hanya dipenuhi oleh 𝑘 = 𝑙 = 1 atau 𝑘 = 𝑙 = −1.
Untuk 𝑘 = 𝑙 = 1 maka 𝑝𝑘 = 𝑞 menjadi 𝑝 = 𝑞.
Untuk 𝑘 = 𝑙 = −1 maka 𝑞𝑙 = 𝑝 menjadi 𝑝(−1) = 𝑞 atau 𝑝 = −𝑞.
Soal Latihan
Jawablah soal-soal berikut. Untuk nomor 1 dan 2, lingkari semua pilihan jawaban yang Anda anggap benar.
1. Diantara yang berikut ini mana sajakah yang benar? a. 2|4 b. 4|2 c. 6|60 d. 60|6 e. 3|(–9) f. (–9)|3
2. Diketahui 5|10. Maka mana sajakah dari yang berikut ini yang benar?
58 a. 5 adalah faktor dari 10.
b. 10 adalah faktor dari 5. c. 5 adalah kelipatan dari 10. d. 10 adalah kelipatan dari 5.
Untuk soal nomor 3 sampai 5, uraikan jawaban Anda.
3. Benarkah jika 𝑝 > 𝑞, maka 𝑝 tidak habis membagi 𝑞?
4. Benarkah jika 𝑝|𝑚 dan 𝑞|𝑛 maka 𝑝𝑞|𝑚𝑛? Jika benar, buktikan dan berikan contohnya.
5. Benarkah jika 𝑝|𝑚 dan 𝑝|𝑛 maka 𝑝|(𝑚 − 𝑛)? Jika benar, buktikan dan berikan contohnya.
59
8. FAKTOR PERSEKUTUAN TERBESAR (FPB)
Tujuan Pembelajaran
Mahasiswa mampu menentukan fpb dari 2 bilangan atau lebih.
Pada Bab Pendahuluan telah dijelaskan makna dari faktor. Pada bab ini akan dibahas tentang faktor persekutuan terbesar (FPB) dari dua bilangan. Untuk itu perhatikan uraian berikut ini.
Bilangan 24 dihasilkan dari perkalian bilangan-bilangan asli berikut. 24 = 1 × 24
= 2 × 12 = 3 × 8 = 4 × 6
Jadi, faktor-faktor dari 24 adalah 1, 2, 3, 4, 6, 8, 12 dan 24.
Bagaimana dengan faktor-faktor dari 36? Bilangan 36 didapatkan dari perkalian bilangan-bilangan asli berikut.
36 = 1 × 36 = 2 × 18 = 3 × 12 = 4 × 9 = 6 × 6
60 Dari jabaran di atas dapat dilihat bahwa faktor-faktor persekutuan dari 24 dan 36 adalah 1, 2, 3, 4, 6 dan 12. Secara umum, istilah faktor persekutuan dapat didefinisikan sebagai berikut.
Definisi faktor persekutuan.
Untuk bilangan bulat 𝑘, 𝑝 dan 𝑞, apabila 𝑘|𝑝 dan 𝑘|𝑞 maka 𝑘 adalah faktor persekutuan dari 𝑝 dan 𝑞.
Telah didapatkan faktor-faktor persekutuan dari 24 dan 36 di atas, yaitu 1, 2, 3, 4, 6 dan 12. Dari fakor-faktor persekutuan ini, manakah faktor persekutuan terbesarnya? Jawabannya adalah 12. Oleh karena itu 12 disebut sebagai faktor persekutuan terbesar (FPB) dari 24 dan 36, ditulis fpb(24, 36) = 12.
Secara umum, istilah FPB dapat didefinisikan sebagai berikut.
Definisi FPB.
Suatu bilangan bulat 𝑟 adalah faktor persekutuan terbesar dari bilangan bulat 𝑝 dan 𝑞, ditulis 𝑟 = fpb(𝑝, 𝑞), apabila 𝑟 lebih besar dari semua faktor-faktor persekutuan 𝑝 dan 𝑞.
Contoh: 1. fpb(3, 12) = .... 2. fpb(15, 24) = .... 3. fpb(45, 60) = .... 4. fpb(9, 23) = .... 5. fpb(17, 25) = ....
61
Catatan. Jika fpb(𝑝, 𝑞) = 1, maka dikatakan 𝑝 dan 𝑞 saling prima
atau 𝑝 prima relatif dengan 𝑞.
Berapakah FPB dari 32 dan 0?
Menggunakan cara yang sama seperti sebelumnya, mula-mula dijabarkan faktor-faktor dari masing-masing 32 dan 0.
32 = 1 × 32 = 2 × 16 = 4 × 8
Jadi, faktor dari 32 adalah 1, 2, 4, 8, 16 dan 32.
Bagaimana dengan faktor-faktor dari 0? 0 = 0 × 0
= 0 × 1 = 0 × 2 = 0 × 3
dan seterusnya.
Jadi faktor dari 0 adalah semua bilangan bulat.
Dapat dilihat bahwa faktor-faktor persekutuan dari 32 dan 0 adalah 1, 2, 4, 8, 16 dan 32. Dan faktor persekutuan terbesarnya adalah 12, ditulis fpb(32, 0) = 32.
62 Tentukanlah: fpb(12, 0) = …. fpb(15, 0) = …. fpb(0, 127) = …. fpb(5374, 0) = …
Ada beberapa cara menentukan FPB dari dua bilangan. Salah satunya adalah dengan cara mendaftarkan faktor-faktor persekutuan dari kedua bilangan tersebut sebagaimana dicontohkan di atas. Cara lainnya adalah dengan pohon faktor atau faktorisasi prima.
Cara-cara ini dapat digunakan untuk menentukan FPB dari dua bilangan yang relatif kecil nilainya. Namun untuk bilangan yang besar, misalnya menentukan FPB dari 31.145 dan 387.597, dibutuhkan cara lain yang lebih efisien. Oleh karena itu berikut ini akan dibahas tentang algoritma pembagian.
Algoritma Pembagian
Untuk memahami tentang algoritma pembagian, terlebih dahulu mari ingat kembali cara pembagian yang diajarkan di SD dengan cara bersusun ke bawah. Misalnya 117 ÷ 31. Soal ini diselesaikan sebagai berikut.
Pada penyelesaian soal di atas, 117 adalah bilangan yang dibagi (dividen), 31 adalah pembagi (divisor), 3 adalah hasil bagi
63 (quotient), dan 24 adalah sisa pembagian (remainder). Jadi pembagian 117 ÷ 31 dapat ditulis sebagai 117
31 = 3 + 24
31. Apabila kedua ruas dikali dengan 31, maka penulisannya menjadi 117 = 31 × 3 + 24.
Secara umum, pembagian 𝑏 oleh 𝑎 dengan hasil bagi 𝑞 dan sisa pembagian 𝑟 dapat ditulis sebagai berikut:
𝑏 𝑎 = 𝑞 + 𝑟 𝑎 atau 𝑏 = 𝑎𝑞 + 𝑟 Contoh: a. 9 : 4 = 9 4 = 2 1 4 atau 9 4= 2 + 1
4 dapat juga ditulis menjadi: 9 = 2 × 4 + 1. b. 16 : 5 = 16 5 = 3 1 5 atau 16 5 = 3 + 1
5 dapat juga ditulis menjadi: 16 = 5 × 3 + 1.
Berkaitan dengan penjabaran di atas, berikut ini diberikan dua teorema yang dapat membantu memudahkan dalam menentukan fpb dari dua bilangan.
Teorema 1.
Untuk bilangan bulat a dan b, dimana a > 0, terdapat satu pasang bilangan bulat q dan r sehingga b = aq + r dengan 0 ≤ r < a , dimana q adalah hasil bagi dan r adalah sisa pembagian b oleh a.
64 Contoh:
1. Misalkan a = 7 dan b = 12, maka 12 : 7 dapat ditulis menjadi 12 = 7q + r. Di sini, q = 1 dan r = 5, yaitu 12 = 7 × 1 + 5.
2. Misalkan a = 4 dan b = 21, maka 21 : 4 dapat ditulis menjadi 21 = 4q + r. Di sini q = 5 dan r = 1, yaitu 21 = 4 × 5 + 1.
3. Misalkan a = 3 dan b = 18, maka 18 : 3 dapat ditulis menjadi 18 = 3q + r. Di sini q = 6 dan r = 0, yaitu 18 = 3 × 6 + 0.
Teorema 2.
Untuk bilangan bulat a, b, q dan r, berlaku aturan berikut ini. Jika b = aq + r, maka fpb(b, a) = fpb(a, r).
Contoh:
1) 12 = 7 × 1 + 5.
Maka menurut teorema di atas, fpb(12, 7) = fpb(7, 5) = 1.
2) 18 = 3 × 6 + 0.
Maka fpb(18, 3) = fpb(3, 0) = 3.
3) 26 = 4 × 6 + 2.
65 Dengan bantuan teorema 1 dan 2, kita dapat menentukan FPB dari dua bilangan a dan b dengan menggunakan algoritma pembagian berkali-kali sehingga kita hanya menentukan FPB dari dua bilangan yang masing-masing lebih kecil dari a dan b. Prosedur penentuan FPB dengan cara ini dinamakan Algoritma Euclid atau Algoritma Pembagian.
Contoh:
1. Gunakan Algoritma Pembagian untuk menentukan FPB dari 24 dan 36.
Jawab
36 = 24 × 1 + 12 24 = 12 × 2 + 0
Menurut Teorema 2, fpb(36,24) = fpb(24, 12) = fpb(12, 0) = 12. Jadi, FPB dari 24 dan 36 adalah 12.
2. Pada sebuah olimpiade, ada 2 kota yang bertanding. Kota A mengirimkan 5767 orang perwakilan dan Kota B, 4453 orang. Jika perwakilan kedua kota dikelompokkan ke dalam beberapa grup yang anggotanya sama banyak,
a. Berapa maksimal grup yang dapat dibentuk?
b. Berapa banyak masing-masing perwakilan Kota A dan Kota B pada tiap grup?
66
Jawab
a. Soal ini adalah soal FPB. Maksimal banyak grup yang dapat dibentuk adalah FPB dari 5767 dan 4453.
5767 = 4453 × 1 + 1314. 4453 = 1314 × 3 + 511 1314 = 511 × 2 + 292 511 = 292 × 1 + 219 292 = 219 × 1 + 73 219 = 73 × 3 + 0 Menurut teorema 2, fpb(5767,4453) = fpb(4453,511) = fpb(511,292) = fpb(292, 219) = fpb(219, 73)= fpb(73, 0) = 73. Jadi FPB dari 5767 dan 4453 adalah 73. Maka maksimal banyak grup yang dapat dibentuk adalah sebanyak 73 grup.
b. Banyak perwakilan dari Kota A pada tiap grup adalah 5767 : 73 = 79 orang; dan Kota B = 4453 : 73 = 61 orang.
3. Coba tentukan FPB dari 260 dan 632. 632 = 260 × …. + ….
260 = 112 × …. + …. 112 = 36 × …. + ….. 36 = 4 × …. + 0
Jadi, fpb(632, 260) = fpb(4, 0) = ....
4. Tentukan FPB dari 314 dan 159. 5. Tentukan fpb(305, 185).
67 Catatan. untuk bilangan bulat a dan b berlaku,
fpb(a, b) = fpb(–a, b) = fpb(a, –b) = fpb(–a, –b).
Algoritma pembagian memudahkan kita menentukan FPB dari dua bilangan. Bagaimana dengan FPB dari tiga bilangan atau lebih? Teorema berikut ini menjelaskan cara menentukan FPB dari tiga bilangan atau lebih.
Teorema 3.
fpb(𝑝1, 𝑝2, 𝑝3,… , 𝑝𝑘) = fpb(fpb(𝑝1, 𝑝2), 𝑝3, … , 𝑝𝑘)
Menurut Teorema 3 di atas, untuk menentukan FPB dari 𝑘 buah bilangan 𝑝1, 𝑝2, sampai dengan 𝑝𝑘, dilakukan dengan menentukan FPB dari dua bilangan terlebih dahulu. Misalkan telah didapatkan fpb(𝑝1, 𝑝2) = 𝑑. Selanjutnya ditentukan fpb(d, 𝑝3), dan seterusnya sehingga pada akhirnya tinggal ditentukan FPB dari dua bilangan saja.
Contoh:
1. Tentukan FPB dari 36, 24, 54 dan 27.
Jawab
fpb(54, 36, 27, 24) = ....
Mula-mula ditentukan FPB dari 2 bilangan, misalkan 54 dan 36. Kedua bilangan ini cukup mudah ditentukan FPB nya
dengan cara biasa atau cara faktorisasi prima. Didapatkan fpb(54, 36) = 9. Selanjutnya ditentukan fpb 9 dan 27, yaitu
68 fpb(9, 27) = 9. Kemudian tinggal dicari fpb dari 9 dan 24, yaitu fpb(9, 24) = 3.
Proses di atas dapat ditulis sebagai berikut. fpb(54, 36, 27, 24) = fpb((fpb(54, 36)), 27, 24) = fpb(9, 27, 24) = fpb((fpb(9, 27)), 24) = fpb(9, 24) = 3
2. Tentukan fpb dari 25, 81, 46 dan 63. 3. Tetukan fpb dari 100, 144 dan 164.
4. Tentukan fpb dari 90, 138, 150 dan 162.
5. Kakak mempunyai 12 pulpen, 36 buku dan 20 pensil dan akan dibagikan ke dalam beberapa parcel yang isinya sama banyak. Berapa maksimal banyak parcel yang dapat Kakak buat? Berapa isi masing-masing pulpen, buku dan pensil pada tiap parcel?
Soal Latihan
Untuk soal-soal berikut ini, tentukan salah atau benar dan berikan alasannya.
1. B – S Sisa pembagian dari 120 : 9 adalah 5.
2. B – S Jika 𝑚|𝑛 dan 𝑝|𝑛 maka 𝑛 adalah faktor persekutuan dari 𝑚 dan 𝑝.
69 3. B – S Diketahui 𝑎 dan 𝑏 mempunyai hanya dua faktor
persekutuan yaitu 𝑟 dan 𝑠. Jika 𝑟 < 𝑠, maka 𝑠 = fpb(𝑎, 𝑏).
4. B –S fpb(921, 654) = 3.
5. B –S fpb(315, 81, 72, 125) = 3.
70
9. KELIPATAN PERSEKUTUAN TERKECIL
(KPK)
Tujuan Pembelajaran
Mahasiswa mampu menentukan kpk dari 2 bilangan atau lebih.
Pada bab sebelumnya telah dibahas mengenai faktor suatu bilangan. Pada bab ini akan dibahas tentang kelipatan bilangan dan kelipatan persekutuan terkecil (KPK) dari dua bilangan.
Konsep kelipatan berkaitan erat dengan konsep faktor. Sebagaimana telah dijabarkan sebelumnya, jika 4 habis membagi 8 maka 4 adalah faktor dari 8. Jelas bahwa 8 diperoleh dari mengalikan 4 dengan suatu bilangan bulat, maka 8 dikatakan sebagai kelipatan dari 4. Berapa sajakah kelipatan dari 4? Kelipatan 4 didapatkan dari mengalikan 4 dengan bilangan bulat lainnya. Namun pada buku ini, pembahasan kelipatan dibatasi pada bilangan asli saja.
4 × 1 = 4 4 × 2 = 8 4 × 3 = 12 4 × 4 = 16 4 × 5 = 20 4 × 6 = 24 dan seterusnya.
Jadi, himpunan kelipatan dari 4 adalah {4, 8, 12, 16, 20, 24, ...}.