Komponen Vektor

1. Pendahuluan

Penggunaan besaran vektor dalam kehidupan sehari-hari sangat penting mengingat aplikasi besaran vektor yang luas. Mulai dari prinsip gaya, hingga bidang teknik dalam memahami konsep medan elektromagnetik. Pada review materi ini, akan dijelaskan mengenai analisis vektor dan sistem koordinat yang merupakan konsep dasar dalam memahami materi medan elektromagnetik.

Analisis besaran vektor memuat tentang pengertian besaran vektor yang akan membandingkannya dengan besaran skalar, komponen vektor, vektor unit (satuan), serta operasi aljabar vektor mengenai penjumlahan, pengurangan, perkalian titik dan silang pada dua vektor.

Sistem koordinat yang akan dibahas yaitu sistem koordinat kartesian (kartesius), sistem koordinat tabung (Cylindrical Coordinates), dan sistem koordinat bola (Spherical Coordinates). Masing-masing sistem koordinat memiliki lambang vektor satuan yang berbeda, namun ketiga sistem koordinat ini dapat dikonversikan ke bentuk sistem koordinat yang lainnya.

2. Vektor dan Skalar

Dalam mempelajari ilmu bidang fisika dan teknik, tentunya menggunakan suatu besaran fisika yang menyatakan suatu nilai terhadap topik yang diteliti. Besaran secara umum dibagi menjadi dua, yaitu skalar dan vektor.

Besaran skalar adalah besaran yang hanya memiliki harga mutlak tanpa menghiraukan arah. Contohnya adalah massa (m), waktu (t), temperatur (T), volume (V), induktansi (L), frekuensi (f), dan sebagainya.

Sedangkan besaran vektor adalah besaran yang selain memiliki nilai, namun juga memiliki arah. Contohnya adalah kecepatan (v), percepatan (a), energi torsi (T), gaya (F), medan listrik (E), dan sebagainya.

3. Komponen Vektor

Komponen suatu vektor menyatakan keberadaan suatu vektor dalam sebuah sistem koordinat. Sebagai ilustrasi dinyatakan bahwa ⃗r memiliki komponen di sumbu x yaitu x, dan berturut-turut di sumbu y dan z yaitu y, z. Ketiga komponen vektor ini merupakan skalar. Untuk lebih jelasnya, komponen vektor merupakan skalar, sedangkan besaran vektor adalah hasil kali skalar vektor tersebut dengan vektor satuannya.pada sumbu tersebut. Hal ini sangat penting untuk operasi vektor, dimana besaran vektor harus diuraikan dalam vektor komponennya. Jadi, vektor komponen adalah hasil kali antara komponen vektor dengan vektor satuan pada sumbu tersebut. Hal ini menunjukkan bahwa vektor komponen merupakan suatu vektor, sedangkan komponen vektor merupakan skalar. Contoh dalam suatu sistem koordinat kartesian terdapat vektor A, maka komponen vektornya adalah x,y,z. A = Axax +

Ayay + Azaz

4. Vektor Unit

Vektor satuan dari ⃗A adalah A` . Vektor satuan adalah vektor yang arahnya sejajar dengan vektor tersebut, namun nilai skalarnya satu. Artinya A` sejajar dengan ⃗A dan

|

_A`

_|

_{=1 . Selain itu, A}` <sub>bersifat tidak bersatuan. Hubungan antara A</sub>` _{dengan |}⃗_A| dinyatakan sebagai: ⃗_A=AA`<sub>=|</sub>⃗<sub>A|A</sub>` Atau ` A=⃗A A

Pada koordinat cartesian, ⃗A dapat dinyatakan dalam komponen sumbu x (Ax),

sumbu y (Ay) dan sumbu z (Az) sebagai:

⃗_{A=`i A}

x+ `j Ay+ `k Az

Dimana `i , `j , dan k` adalah vektor satuan berturut-turut pada sumbu x,y, dan z. Berdasarkan dalil Phytagoras, nilai skalar dari ⃗A adalah:

A=

√

Ax 2 +Ay 2 +Az 2

Maka vektor satuannya dapat ditulis: ` A=

[

`i Ax+ `j Ay+ `k Az

]

√

A_x2 +A_y2 +A_z2 5. Penjumlahan Vektor

Dua buah vektor dikatakan sama apabila kedua vektor tersebut besar serta arahnya sama, oleh sebab itu sebuah vektor dapat digerakkan asal panjang dan arahnya tidak berubah. Pernjumlahan dari dua buah vektor ditunjukkan seperti pada gambar:

Gambar 1. Penjumlahan Dua Vektor Vektor C merupakan vektor hasil penjumlahan dari vektor A + B:

C=A+B=B+A

Dengan besar nilai C yaitu: C2

=A2_+B2_−2ABcosθ C=

√

A2+B2−2ABcosθ

Serta besar sudut vektor C dan A diperoleh dari hubungan: sinα

B =

sinθ C

Sehingga besar sudut antara vektor C dan A diperoleh: α=B

Csin −1

θ

Metode lain untuk menghitung jumlah dari dua buah vektor yaitu dengan mencari diagonal kongruen jajaran genjang dimana sisi-sisinya merupakan vektor yang akan dijumlahkan. Misalkan vektor A dan B, dengan cara menarik vektor A dan B ke titik pangkal yang sama seperti pada gambar:

Gambar 2. Metode Jajaran Genjang

Perkalian skalar dengan besaran vektor memenuhi hukum-hukum dibawah ini, yaitu: a. Hukum asosiatif, yaitu (k+l)(A+B) = k(A+B) + l (A+B), dengan k dan l adalah

bilangan skalar.

b. Hukum distributif, yaitu apabila (k+l)(A+B) = (kA+kB+lA+lB).

Sedangkan penjumlahan dua atau lebih vektor memenuhi hukum-hukum dibawah ini, yaitu:

a. Hukum komutatif, yaitu(A+B) = (B+A)

b. Hukum asosiatif, yaitu A+(B+C) = (A+B)+C = (A+C)+B

6. Pengurangan Vektor

Pengurangan vektor dengan vektor lain sama halnya dengan penambahan vektor negatif pengurang dimana dalam hal ini vektor negatif didefinisikan sebagai vektor yang besarnya sama tetapi arahnya berlawanan dengan vektor tersebut, misalnya:

A−B=A+(−B)

7. Perkalian dan Pembagian Vektor

Perkalian pada vekor dibagi menjadi perkalian titik (dot product) dan perkalian silang (cross product).

8. Perkalian Titik Dua Vektor

Apabila diketahui tiga buah vektor yaitu A, B, dan C merupakan vektor dalam ruang dimensi tiga, serta s merupakan skalar, maka:

a. A ∙ B=B ∙ A b. A ∙ B=|A||B|cosθ c. (A+B)∙ C=A ∙C+B ∙C d. A ∙ A=0,jika A=0 e. A ∙ A=|A|2≥0 f. (sA)∙ B=s(A ∙ B)=A ∙(sB)

g. A ∙ B=0,jika dan hanya jika A dan B berpotongan

Selanjutnya kaidah yang ditunjukkan dibawah ini dimana i, j, dan k merupakan vektor satuan di ruang xyz:

h. i∙ i=j ∙ j=k ∙ k=1

i. i∙ j=i ∙ k=j∙ k=0, persamaan ini merupakan perpotongan vektor satuan. Melalui hasil dot product pada pada vektor di ruang xyz maka akan diperoleh proyeksi skalar kedua vektor tersebut. Sebagai contoh yaitu compBA yang didefinisikan sebagai

proyeksi vektor A dalam arah vektor B. comp_BA=A ∙ B

|B| 9. Perkalian Silang Dua Vektor

Perkalian silang dua buah vektor antara vektor A dan B didefinisikan sebagai besarnya vektor A dikalikan dengan besar vektor B dan dikalikan dengan sinus sudut terkecil yang terbentuk oleh vektor A dan B yang secara matematis dijabarkan sebagai berikut:

A × B=|A||B|sinθ

Cross product bukanlah operasi komutatif sehingga memenuhi persamaan: B × A=−(A × B)

Vektor satuan ax dengan ay berpotongan, maka akan merentangkan bidang dalam satuan

luas. Hal ini mengikuti kaidah ketiga jari tangan bahwa: a_x× a_y=a_{z , sedangkan} a_y× a_x=−a_z

Berdasarkan pada penjelasan diatas, cross product untuk vektor satuan ax, ay, dan az

dapat dikembangkan menjadi:

a_y× a_z=a_{x , sedangkan} a_z×a_y=−a_x a_z×a_x=a_{y , sedangkan} a_x× a_z=−a_y a_x× a_x=0 _,

a_y× a_y=0 _, a_z×a_z=0 _.

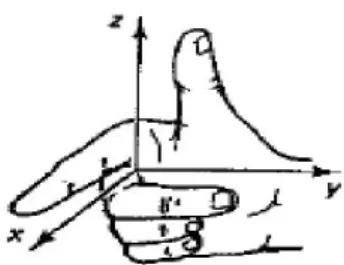
Cross product dua buah vektor dalam ruang dapat menentukan dengan jelas nilai dan arah vektor. Konsepnya adalah tiga garis vektor yang berdiri sendiri misalnya A, B, dan C mengikuti kaidah tiga jari pada tangan kanan. Dalam hal ini vektor A, B, dan C berturut-turut adalah ibu jari, kelingking, dan jari tengah yang diluruskan secara bersamaan. Begitu pula halnya untuk vektor standar dasar yaitu i, j, dan k dapat mengikuti kaidah pada ketiga jari kanan seperti pada gambar:

Gambar 4. Kaidah Tangan Kanan Pada Vektor

10. Sistem Koordinat Kartesian

Koordinat kartesian digunakan untuk menyatakan suatu benda yang memiliki bentuk siku seperti garis lurus, bidang datar siku dan ruang siku-siku. Bentuk bentuk siku akan mudah digambarkan dalam koordinat kartesius baik 2 dimensi maupun 3 dimensi.

Koordinat kartesius 3 dimensi digunakan untuk menggambarkan suatu objek baik 1 dimensi, 2 dimensi maupun 3 dimensi. Koordinat kartesius 3 dimensi mempunyai 3 sumbu koordinat yaitu sumbu x, y, dan z. Untuk lebih jelasnya silahkan perhatikan gambar berikut :

Sudut yang dibentuk antar sumbu koordinat adalah 90o _{atau dengan kata lainsumbu x}

tegak lurus dengan sumbu y dan sumbu z, demikian juga sumbu y tegak lurus dengan sumbu x dan z dan juga sumbu z tegak lurus dengan sumbu x dan sumbu y.

Gambar 8. Hubungan Tegak Lurus Pada Koordinat Kartesian

Persamaan vektor pada koordinat kartesian adalah sebagai berikut: ⃗_A=A

xa^x+Aya^y+Aza^z dengan a^x , a^y , dan a^z masing-masing adalah vektor

satuan dari sumbu x, y, dan z.

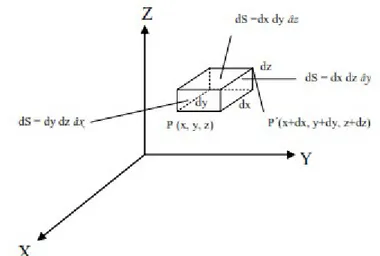
Pada sistem koordinat kartesian, terdapat tiga macam elemen yang membangun koordinat tersebut, yaitu elemen garis, permukaan, dan volume.

a. Elemen Garis

Elemen garis merupakan diagonal yang melawati titik P, dengan persamaan dl=dxa^x+dya^y+dza^z _atau dl2=dx2+dy2+dz2 _.

b. Elemen Permukaan

Elemen permukaan adalah suatu elemen yang terbentuk dari elemen-elemen garis (dl), dengan persamaan ds=± dl1× dl2 .

Dimana dalam hal ini berlaku hubungan:

 Permukaan depan : ± dya^y× dza^z=dy dza^x

 Permukaan samping : ± dxa^x× dza^z=dx dza^y

 Permukaan alas : ± dya^y× dxa^x=dy dxa^z

c. Elemen Volume

Elemen volume merupakan bagian-bagian yang terbentuk dari elemen-elemen permukaan (ds), dengan persamaan dV=dl1× dl2× dl3 . Pada setiap permukaannya, akan menghasilkan besar dV = dx × dy × dz.

11. Sistem Koordinat Tabung

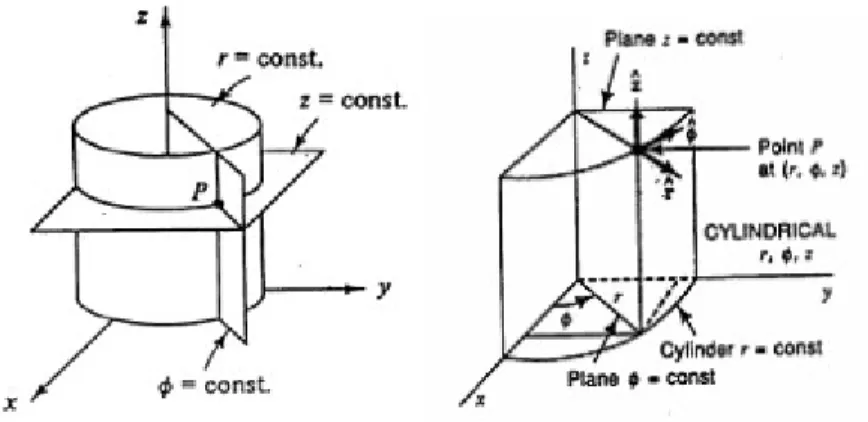
Tidak semua benda mempunyai bentuk siku-siku seperti balok, kubus, bujur sangkar, dan bentuk-bentuk siku lainnya. Benda-benda seperti tabung, botol, pipa, tampat sampah, kerucut memiliki bentuk lingkaran dengan simetri yang khas. Bentuk-bentuk seperti ini akan susah untuk digambarkan pada koordinat kartesius karena simetri lingkaran sulit untuk digambarkan. Atas dasar inilah muncullah ide untuk mengembangkan system koordinat untuk benda-benda seperti ini yaitu dengan membuat koordinat silinder. Koordinat silinder terdiri dari 3 sumbu koordinat yaitu koordinat r, , dan z. ϕ

Dengan masing-masing vektor satuan ke arah r, , dan z aalah sebagai berikut:ϕ a_r=r

a_ϕ=ϕ

a_z=z

Dengan opersai aljabar vektor yang berlaku adalah sebagai berikut:

 ar× aϕ=az , sedangkan aϕ× ar=−az

 aϕ× az=ar , sedangkan az×aϕ=−ar

 az×ar=aϕ , sedangkan ar× az=−aϕ

Gambar 10. Penjabaran Vektor Dalam Sistem Koordinat Tabung

Konversi dari koordinat silinder ke koordinat kartesian adalah sebagai berikut : x = r cos ,ϕ

y = r sin , ϕ z = z

Sedangkan konversi dari koordinat kartesian ke silinder adalah sebagai berikut: r=

√

x2+y2

ϕ=tan−1

(

y x

)

z = z

Seperti pada sistem koordinat kartesian, sistem koordinat tabung juga memiliki vektor satuan yang mempunyai harga absolutnya sama dengan satu. Hubungan antara vektor satuan pada koordinat kartesian dengan koordinat tabung dipaparkan melalui persamaan matriks berikut:

[

a^_r ^ a_ϕ ^ a_z

]

=

[

cosϕ sinϕ 0 −sinϕ cosϕ 0 0 0 1

]

[

^ a_x ^ a_y ^ a_z

]

Untuk mendapatkan hubungan baliknya, maka digunakan invers matriks dari hubungan diatas. Diketahui harga determinan matriks tersebut adalah 1, maka diperoleh invers matriks tersebut akan sama dengan matriks transposenya, sehingga persamaan matriksnya menjadi:

[

a^_x ^ a_y ^ a_z

]

=

[

cosϕ −sinϕ 0 sinϕ cosϕ 0 0 0 1

]

[

^ a_r ^ a_ϕ ^ a_z

]

Contoh visualisi penggambaran objek dalam koordinat silinder untuk kasus, r konstan, konstan dan z konstan. Dari gambar ini dapat dibayangkan kira-kira suatu objek yang ϕ

Gambar 9. Visualisasi Koordinat Tabung

Pada sistem koordinat tabung, terdapat elemen-elemen penyusun sistem koordinat tersebut yaitu elemen garis, permukaan, dan volume yang dijabarkan sebagai berikut:

a. Elemen Garis ∂ l=∂ ra^r+r ∂ϕa^ϕ+∂ za^z ∂ l2=∂ r2+r2∂ϕ2+∂ z2 b. Elemen Permukaan  Selimut tabung : r ∂ϕ∂ z  Alas : r ∂ r ∂ϕ

 Sisi perpotongan alas dengan selimut : ∂ r ∂ z c. Elemen Volume

∂ V=(∂ r)(r ∂ϕ)(∂ z) ∂ V=r ∂ r ∂ϕ∂ z

12. Sistem Koordinat Bola

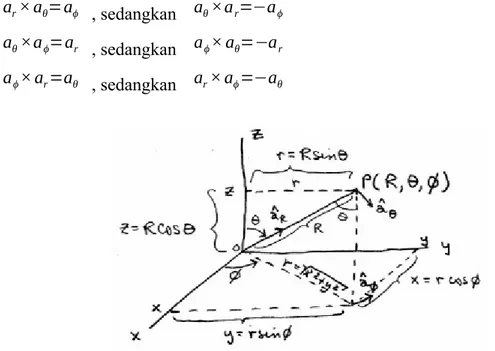
Koordinat bola digunakan untuk menyatakan suatu objek yang mempunyai bentuk simetri bola. Sebagai contoh adalah bumi yang kita tempati. Posisi atau kedudukan objek-objek yang berada dibumi akan sulit dijelaskan dengan koordinat kartesius maupun tabung karena bentuk bumi yang bundar. Oleh karena itu digunakan system koordinat bola agar mudah dibayangkan. Untuk menyatakan besaran vektor, koordinat bola menggunakan 3 sumbu koordinat yaitu r,θ, dan .ϕ

Gambar 10. Sistem Koordinat Bola

Pada sistem koordinat bola, terdapat vektor satuan dalam arah r, θ, dan berturut-turutϕ adalah ar, aθ, dan aϕ dengan persamaan operasi perkalian vektor satuannya adalah sebagai

berikut:

a_r× a_θ=a_{ϕ , sedangkan} a_θ×a_r=−a_ϕ a_θ×a_ϕ=a_{r , sedangkan} a_ϕ× a_θ=−a_r aϕ× ar=aθ , sedangkan ar× aϕ=−aθ

Gambar 11. Komponen Vektor Dalam Sistem Koordinat Bola Sehingga sebuah vektor pada sistem koordinat bola didefinisikan pada persamaan:

⃗_A=A

ra^r+Aθa^θ+Aϕa^ϕ

Konversi koordinat kartesian ke koordinat bola adalah sebagai berikut: r=

√

x2+y2+z2 θ=tan−1

(

rsinθ z

)

=tan −1

(

√

x2+y2 z

)

ϕ=tan−1

(

y x

)

Sistem koordinat bola juga memiliki vektor satuan yang harga absolutnya sama dengan 1 (satu).

Gambar 12.

Apabila dihubungkan dengan vektor satuan pada sistem koordinat kartesian, maka diperoleh persamaan matriks sebagai berikut:

[

a^_r ^ a_θ ^ a_ϕ

]

=

[

sinθcosϕ sinθsinϕ cosθ cosθcosϕ cosθsinϕ −sinθ

−sinϕ cosϕ 0

]

[

^ a_x ^ a_y ^ a_z

]

Apabila ingin mendapatkan koordinat kartesiannya maka digunakan matriks transpose menjadi:

[

a^_x ^ a_y ^ a_z

]

=

[

sinθcosϕ cosθcosϕ −sinϕ

sinθsinϕ cosθsinϕ cosϕ

cosθ −sinθ 0

]

[

^ a_r ^ a_θ ^ a_ϕ

]

Serupa dengan sistem koordinat yang lainnya, pada sistem koordinat bola memiliki tiga elemen penyusunnya, yaitu garis, permukaan, dan volume yang digambarkan pada sketsa berikut:

Gambar 13. a. Elemen garis diferensial

Elemen garis diferensial pada koordinat bola memiliki persamaan: ∂ l=∂ ra^_r+r ∂θa^_θ+rsinθ ∂ϕa^_ϕ

b. Elemen permukaan diferensial:

∂ s=r ∂ r ∂ θ+rsinθ ∂ r∂ϕ+r2sinθ ∂ θ ∂ϕ

c. Elemen volume diferensial ∂ V=r2sinθ ∂ r ∂θ ∂ϕ