Medan Skalar dan Medan Vektor

1. Medan Skalar dan Medan Vektor. Pengantar Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Capaian Belajar • Memahami medan skalar dan penerapannya dalam masalah Teknik sipil. • Memahami medan vektor dan penerapannya dalam perilaku aliran dan parameter terkait seperti kecepatan dan debit.. EDUNEX ITB.

3. Sub Topik • Pengertian medan skalar, • Turunan parsial,. • Arti fisis dan geometri vektor gradien, • Turunan berarah, arti fisis dan geometri turunan berarah. • Medan vektor, pengertian medan vector, berbagai contoh medan vektor, • Divergensi dan rotasi medan • Flux dan perhitungan debit aliran. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Medan Vektor Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Medan Vektor [Definisi] • Jika setiap titik P (x,y,z) berada pada ruang R, berhubungan dengan fungsi vektor F(x,y,z), maka medan vektor disebut eksis pada ruang R. • •. Fungsi Vektor : F(x, y, z)=Fxi+Fyj+Fzk Fungsi vektor mendefinisikan medan vektor pada daerah definisinya. Contoh medan vektor adalah medan vektor kecepatan dan medan vektor gravitasi.. EDUNEX ITB.

3. Contoh Medan Vektor [2D] • Anggap terdapat fungsi F(x,y)=(y,-x) • Sehingga kita dapat mengambarkan fungsi vektor diatas sebagai berikut : • F(1,0)=[0,-1] • F(0,1)=[1,0] • F(1,1)=[1,-1]. EDUNEX ITB.

4. Contoh Medan Vektor [2D] • Jika dibuat dalam jumlah yang lebih banyak maka medan vektor dari fungsi F dapat digambarkan sebagai berikut:. EDUNEX ITB.

5. Contoh Medan Vektor [3D] F(x,y)=(y,-x,z). EDUNEX ITB.

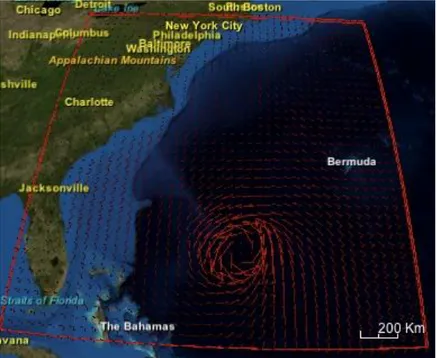
6. Ilustrasi Medan Vektor Badai Katrina. Medan Vektornya. https://people.eecs.ku.edu/~jrmiller/WorldWindProjects/VectorFieldVis/ EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Medan Skalar Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Medan Skalar [Definisi] • Jika setiap titik di P (x,y,z) berada pada ruang R, berhubungan dengan besaran skalar φ(x,y,z), kemudian φ(x,y,z) adalah fungsi skalar, maka medan skalar disebut eksis pada ruang R. • •. Fungsi Skalar : f=f(P) Fungsi skalar mendefinisikan medan skalar pada daerah definisinya. Contoh medan skalar adalah medan temperatur tubuh, medan tekanan udara di atmosfir. EDUNEX ITB.

3. Ilustrasi Medan Skalar s(x,y)=(y,-x). EDUNEX ITB.

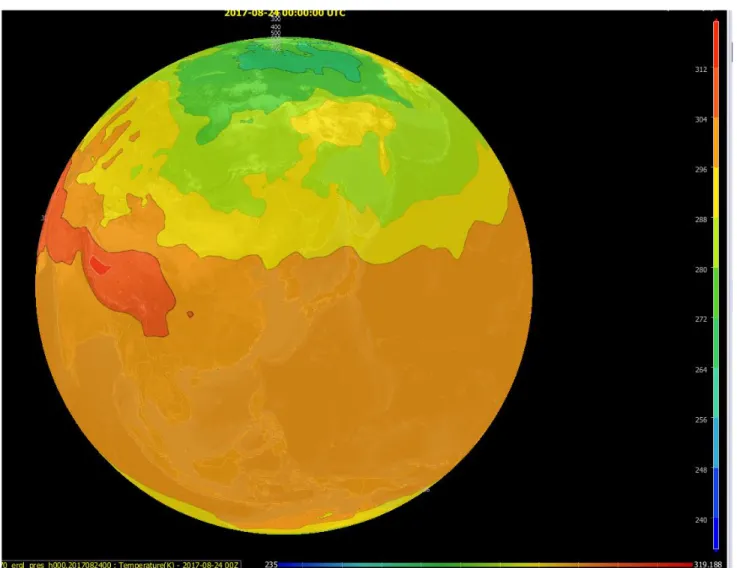
4. Ilustrasi Medan Skalar • Medan temperature bumi? • Peta topografi?. EDUNEX ITB.

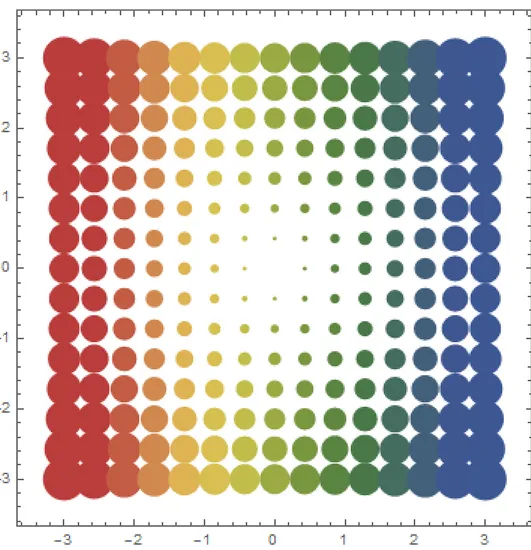
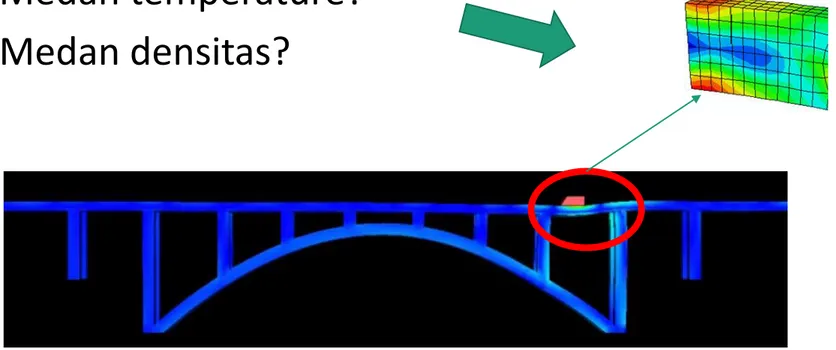
5. Ilustrasi Medan Skalar • Medan temperature? • Medan densitas?. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Turunan Vektor Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Parametric Representation. A(t). 𝐀(𝑡) = 𝑎𝑥 (𝑡)𝐢 + 𝑎𝑦 (𝑡)𝐣 + 𝑎𝑧 (𝑡)𝐤. EDUNEX ITB.

3. Parametric Representation. https://www.khanacademy.o rg/math/ap-calculus-bc/bcadvanced-functions-new/bc9-4/v/position-vectorvalued-functions. EDUNEX ITB.

4. Turunan dari Vektor [1] • Jika vektor A tergantung pada variabel skalar t, kemudian A dapat direpresentasikan sebagai A(t) dan dapat dikatakan bahwa A merupakan fungsi dari t. • Dalam koordinat tiga dimensi, fungsi vektor ini dapat dituliskan sebagai berikut:. = a x (t )i + a y (t ) j + a z (t )k. EDUNEX ITB.

5. Turunan dari Vektor [2] • Vektor A(t) dikatakan bisa diturunkan (i.e., differentiable) pada titik t jika limit dari persamaan berikut berlaku. A(t + t ) − A(t ) A' (t ) = lim t t →0. A(t+Δt). • Vektor A’(t) ini disebut sebagai turunan dari A(t). https://youtu.be/E9Q_Lc0g1xE. A. EDUNEX ITB.

6. Turunan dari Vektor [3] • Jika terdapat A=axi+ayj+azk, kemudian ax,ay,az juga tergantung kepada parameter t • Yaitu A(t)=ax(t)i+ ay(t)j+ az(t)k • Turunan dari vektor A(t) adalah:. . . d d d d A(t ) = i a x (t )+ j a y (t ) + k a z (t ) dt dt dt dt da y da x dA da z =i +j +k dt dt dt dt da y da x dA da z Persamaan Umum =i +j +k du du du du. EDUNEX ITB.

6. Contoh Turunan Vektor A = (3u 2 + 4)i + (2u − 5) j + 4u 3k dA = 6ui + 2 j + 12u 2k du d 2A du 2. = 6i + 24uk. • Jika u=2, maka. dA = .... ? du d 2A du. 2. = .... ? EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Vektor Singgung Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Vektor Singgung Satuan • Jika r adalah vektor yang menghubungkan titik asal (0,0,0) pada suatu sistem koordinat dengan titik (x,y,z), dimana r merupakan fungsi dari t, r(t). • Garis singgung kurva terhadap C di P didefinisikan sebagai garis melalui P yang sejajar terhadap vektor singgung r'(t). • Jika skalar h diambil sebagai perubahan posisi vektor pada busur s yang diukur dari suatu titik pada C.. EDUNEX ITB.

2. Vektor Singgung Satuan Jika titik P dan Q mempunyai vektor posisi. r(t+h) – r(t). z. r(t) r'(t) P. maka r(t+h). - r(t). menyatakan vektor PQ . Pada saat h → 0. Q. vektor ini mendekati vektor yang terletak pada garis singgungnya. Vektor r'(t) disebut. r(t). vektor singgung kurva yang diberikan oleh r. r(t+h). C. dan r(t+h),. di titik P. 0 x. y EDUNEX ITB.

4. Unit Vektor/Vektor Satuan • suatu vektor dengan panjang "satu ". r aˆ = r • Contoh:. r = 3,4  r 3i + 4 j 3i + 4 j aˆ = = = 2 2 r 5 3 +4 EDUNEX ITB.

5. Vektor Singgung Satuan Maka Vektor singgung satuan diberikan oleh :. 𝑑𝐫 𝐫′(𝑡) 𝑑𝑡 𝐓(𝑡) = = 𝑑𝐫 𝐫′(𝑡) 𝑑𝑡. EDUNEX ITB.

Contoh Vektor Singgung Satuan • Jika r(t) = (3t2-1)i +(t2+1)j+t2k tentukan vektor singgung satuan pada titik t=1? dr r ' (t ) T(t ) = = dt dr r ' (t ) dt. (. ). dr d = 3t 2 − 1 i + (t 2 + 1) j + t 2k dt dt = 6ti + 2t j + 2tk. t: parametric at curve. . dr = (6t ) 2 + (2t ) 2 + (2t ) 2 = 44t 2 = t 44 dt T(t ) =. 6ti + 2t j + 2tk t 44. T(1) =. 6i + 2 j + 2k 44. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Turunan Parsial Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Turunan Parsial • Turunan parsial untuk fungsi vektor dua variabel atau lebih, prinsipnya sama dengan definisi turunan fungsi vektor satu variabel, dimana semua variabel dianggap konstan, kecuali variabel terhadap apa fungsi vektor itu diturunkan. • Misalkan A adalah sebuah fungsi vektor yang tergantung kepada variabel skalar x, y, dan z, maka dapat ditulis sebagai A = A(x,y,z). Ketiga turunan parsialnya didefinisikan sebagai berikut:. EDUNEX ITB.

3. Turunan Parsial. • adalah masing-masing turunan parsial dari A terhadap x, y, dan z, jika limitnya ada.. EDUNEX ITB.

4. Turunan Parsial • Jika fungsi vektor 𝐀 (𝑥,𝑦,𝑧)=A1(𝑥,𝑦,𝑧)𝐢+A2(𝑥,𝑦,𝑧)+A3(𝑥,𝑦,𝑧)𝐤 • dengan fungsi skalar A1(𝑥,𝑦,𝑧), A2(𝑥,𝑦,𝑧), dan A3(𝑥,𝑦,𝑧)mempunyai turunan parsial terhadap variabel x, y, dan z, maka juga mempunyai turunan variabel terhadap x, y, dan z yang dirumuskan sebagai berikut :. EDUNEX ITB.

5. Turunan Parsial. • Jika A dan B adalah fungsi-fungsi vektor dan φ adalah fungsi skalar x, y, dan z yang dapat diturunkan terhadap ketiga variabel tersebut . EDUNEX ITB.

6. Contoh Turunan Parsial • Jika F=2xyi+(x2-2y)j+(x+y2)k F = 2 yi + 2 xj + k x.  2F x 2. = 2j. F = 2 xi − 2 j + 2 yk y.  2F = 2i xy. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Gradient of Scalar Field Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Gradient Using scalar fields instead of vector fields is of a considerable advantage because scalar fields are easier to use than vector fields, “gradient” that allows us to obtain vector fields from scalar fields (kreyzig). EDUNEX ITB.

3. Gradient The gradient of a scalar field V is a vector that represents the magnitude and the direction of the greatest increase rate of V.. EDUNEX ITB.

4. Gradient • Gradien adalah kata lain dari turunan/tingkat perubahan fungsi. • Kata ini merujuk kepada arah pergerakan yang: ✓Menunjuk ke arah peningkatan terbesar dari suatu fungsi ✓Bernilai nol pada minimum lokal atau maximum lokal (karena tidak ada satu arah peningkatan). EDUNEX ITB.

5. Gradient A. b. https://youtu.be/Z TbTYEMvo10. EDUNEX ITB.

6. • Ruangan tertutup dengan AC mungkin memiliki temperature yang tidak homogen pada setiap titik koordinatnya.. Contoh Sederhana. • Gradien dapat digunakan untuk menunjukkan arah perubahan suhu kepada tingkat suhu yang tertinggi. • Informasi ini mungkin berguna untuk menentukan arah AC EDUNEX ITB.

7. Contoh Sederhana Sumber : https://betterexplained.com/articles/vectorcalculus-understanding-the-gradient/. “Menentukan titik koordinat dalam microwave untuk memasak kue dengan waktu masak tercepat.”. EDUNEX ITB.

8. Gradient • Jika fungsi skalar f terdiferensiasi pada setiap titik (x,y,z) dalam ruang R3, maka gradien f atau grad f atau 𝛁f didefinisikan oleh :  f f f  f f f grad f = f =  , ,  = i+ j+ k y z  x y z  x. • Kemudian gradien dari fungsi f merupakan fungsi vektor. Dimana operator turunan 𝛁 (dibaca : nabla/del) dapat didefinisikan sebagai:    = i+ j+ k x y z EDUNEX ITB.

9. Gradient • Contoh: (1). f ( x, y, z ) = 2 y 3 + 4 xz + 3 x f f f f = i+ j+ k x y z f = (4 z + 3)i + 6 y 2 j + 4 xk. (2) f=2x2yz3 grad f = 4xyz3i + 2x2z3j + 6x2yz2k EDUNEX ITB.

1. Medan Skalar dan Medan Vektor Turunan Berarah (Visualisasi) Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Medan skalar z(x,y). • Geser titik searah sumbu y ✓Nilai z (lingk. Kuning) akan berubah mengikuti arah slopenya (lingk. Merah).. • Kondisi ini menjelaskan partial derivative z pada sumbu y searah sumbu y. https://mathinsight.org/directional_ derivative_gradient_introduction EDUNEX ITB.

3 • Geser titik searah sumbu x ✓Nilai z (lingk. Kuning) akan berubah mengikuti arah slopenya (lingk. Merah).. • Kondisi ini menjelaskan partial derivative z pada sumbu x searah sumbu x. https://mathinsight.org/directional_ derivative_gradient_introduction EDUNEX ITB.

4. Turunan Berarah • Bagaimana jika turunan pada arah vektor tertentu?. searah vector u. https://mathinsight.org/directional_ derivative_gradient_introduction. EDUNEX ITB.

5. Turunan Berarah • Turunan-turunan parsial fx (x, y) dan fy (x, y) mengukur laju perubahan (dan kemiringan garis singgung) pada arah sejajar dengan sumbu x atau sumbu y saja. • Pada materi ini akan dipelajari laju perubahan f pada arah-arah tersebut secara simultan.. https://www.youtube.com/watch?v=GkB4vW16QHI EDUNEX ITB.

1. Medan Skalar dan Medan Vektor Turunan Berarah (Perhitungan) Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Turunan Berarah • Turunan-turunan parsial fx (x, y) dan fy (x, y) mengukur laju perubahan (dan kemiringan garis singgung) pada arah sejajar dengan sumbu x atau sumbu y saja. • Pada materi ini akan dipelajari laju perubahan f pada arah-arah tersebut secara simultan.. https://www.youtube.com/watch?v=GkB4vW16QHI EDUNEX ITB.

3. Turunan Berarah • Sebagai contoh, anggap terdapat fungsi f yang memiliki tingkat perubahan pada arah x dan y. Anggap, perubahan pada arah x dua kali lebih besar daripada arah y. • Arah perubahan tersebut dapat dilambangkan menggunakan vektor v <2,1>. Meskipun terdapat banyak sekalian variasi dari vektor yang memiliki arah seperti vektor v <2,1>.. EDUNEX ITB.

4. Turunan Berarah • Oleh karenanya digunakan definisi vektor satuan. v v = vˆ = v. • Sehingga vektor satuan tersebut adalah:. EDUNEX ITB.

5. Turunan Berarah. EDUNEX ITB.

6. Turunan Berarah. EDUNEX ITB.

7. Turunan Berarah. EDUNEX ITB.

8. Turunan Berarah • Tentukan turunan berarah dari fungsi berikut f=x2z + 2xy2 + yz2 pada titik (1,2,-1) dan arah vektor A=2i+3j-4k (i) Tentukan grad f pada titik (1,2,-1) f = (2 xz + 2 y 2 )i + (4 xy + z 2 ) j + ( z 2 + 2 yz )k f = (−2 + 8)i + (8 + 1) j + (1 − 4)k f = 6i + 9 j − 3k. (ii) Tentukan a dari vektor A=2i+3j-4k A = 2i + 3 j − 4k  A = 4 + 9 + 16 = 29 a=. A 1 = (2i + 3 j − 4k ) A 29. EDUNEX ITB.

9. Turunan Berarah (iii) Tentukan turunan berarahnya Da f ( x, y, z ) = a.f = Da f ( x, y, z ) =. 1 29. 1 29. (2i + 3 j − 4k ).(6i + 9 j − 3k ). (12 + 27 + 12) =. 51 29. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Divergensi (Arti Fisis) Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Arti Fisis Divergensi. https://youtu.be/rB83 DpBJQsE EDUNEX ITB.

3. Arti Fisis Divergensi div F (x,y)>0. div F (x,y)<0. Medan Vektor F(x,y) (x,y). div F(x,y) menunjukkan seberapa banyak “aliran imajinatif” “masuk” ataupun “keluar” titik (x,y) pada medan vektor F https://youtu.be/rB83 DpBJQsE EDUNEX ITB.

4. Arti Fisis Divergensi. (x,y). • Memiliki divergensi positif dititik (x,y) karena arus keluar > arus yang masuk EDUNEX ITB.

5. Arti Fisis Divergensi. • Memiliki divergensi =0 di setiap tempat EDUNEX ITB.

6. Arti Fisis Divergensi. Arus yang masuk = yang keluar https://youtu.be/qOcFJKQPZfo EDUNEX ITB.

7. Arti Fisis Divergensi. https://www.khanacademy.org/math/multivariablecalculus/multivariable-derivatives/divergence-and-curlarticles/a/divergence EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Divergensi (Perhitungan) Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Divergensi [1] • Dari medan skalar kita dapat memperoleh medan vektor melalui gradien. • Sementara dari medan vektor kita dapat memperoleh medan skalar dengan menggunakan divergensi, atau medan vektor lainnya dengan curl. • Operator  • dapat diaplikasikan kepada vektor fungsi A (x,y,z) untuk mendapatkan divergensi dari A, yang biasa disingkat sebagai div A. EDUNEX ITB.

3. Divergensi [2] A = axi + a y j + azk      div A = .A =  i + j + k .(a x i + a y j + a z k ) y z   x a x a y a z div A = .A = + + x y z. • Operator del pada skalar memberikan fungsi vektor • Operator div pada vektor memberikan fungsi skalar EDUNEX ITB.

4. Divergensi [3] • Contoh Tentukan divergensi dari fungsi A=x2yi - xyzj + yz2k. a x a y a z div A = .A = + + x y z div A = .A = 2 xy − xz + 2 yz. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Flux Aliran Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Arti Fisis Divergensi • Secara umum arti fisis dari divergensi dapat dilihat dari perhitungan untuk mengetahui perubahan/laju dari suatu vektor dalam arah x, y dan z. (outflow dikurangi inflow). Ain. Aout. EDUNEX ITB.

3. Arti Fisis Divergensi • Salah satu contoh dari pengunaan divergensi adalah penggunaan dalam teori kekekalan massa pada fluida. • Anggap terdapat fluida dengan density ρ yang tergantung kepada koordinat x,y,z pada ruang dan juga tergantung kepada waktu t. Anggap bahwa arus tersebut melalui sebuah kotak B dengan ukuran Δx, Δy, Δz yang memiliki volume ΔV=ΔxΔyΔz EDUNEX ITB.

4. Arti Fisis Divergensi • Anggap bahwa vektor kecepatan aliran kontinu dan terdiferensiasi, dimana : v = [v1, v2 , v3 ] = v1i + v2 j + v3k. 𝜌=mass per unit volume. • Maka vektor arusnya adalah sebagai berikut : 𝐮 = [𝑢1 , 𝑢2 , 𝑢3 ] = 𝑢1 𝐢 + 𝑢2 𝐣 + 𝑢3 𝐤 = 𝜌𝐯. • Kemudian total kehilangan massa yang meninggalkan B per satuan waktu dapat dihitung dengan mempertimbangkan fluks pada penampang kotak B. EDUNEX ITB.

5. Arti Fisis Divergensi • Karena vektor v1i dan v3k tegak paralel terhadap bidang permukaan, maka kontribusi dari kedua komponen tersebut tidak ada pada aliran arus searah sumbu y. • Sehingga massa fluida yang masuk kedalam bidang permukaan pada waktu pendek (Δt) dapat diestimasi sebagai. (v2 )y x z t = (u2 )y x z t Massa dari fluida yang meninggalkan kotak B pada bidang permukaan selama kurun waktu tertentu adalah (u2 ) x z t y + y. EDUNEX ITB.

6. Arti Fisis Divergensi • Selisih antara inflow dan outflow kemudian diestimasi sebagai kehilangan massa fluida: = u2 x z t dimana u2 = (u2 ) y + y − (u2 ) y u2 = y x z t y u2 = Vt y Ain. Aout EDUNEX ITB.

7. Arti Fisis Divergensi. Pada seluruh arah sumbu. • Kemudian total kehilangan massa pada interval Δt dapat diestimasi sebagai:  u1 u2 u3     x + y + z Vt  . (1). • Total kehilangan massa dapat diartikan juga sebagai tingkat perubahan densitas per satuan waktu  − Vt t. (2). EDUNEX ITB.

8. Arti Fisis Divergensi. A = axi + a y j + azk  u1 u2 u3    Vt = − + + Vt        • Dengan menyamakan persamaan (1) dan (2) diperoleh :  x  y  z  t  div A =  . A = i + j + k .(a x    x y z.  u1 u2 u3      x + y + z  = − t    div u = − t  div u + =0 t. . . a x a y a z div A = .A = + + x y z. condition for the conservation of mass or the continuity equation of a compressible fluid flow EDUNEX ITB.

10. Arti Fisis Divergensi • Jika arus dalam keadaan steady, yaitu alirannya tidak tergantung waktu (i.e., t = 0), maka: div 𝐮 = 0 div(𝜌𝐯) = 0 • Jika densitas arus konstan (i.e., , fluida bersifat inkompresible, tidak berubah dalam tekanan), maka div v = 0. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Arti Fisis Curl Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Curl (Medan Rotasi) • Anggap terdapat medan vector F yang merepresentasikan fluida • Dapat meng-capture bagaimana fluida berotasi ✓ Anggap terdapat bola yang dipatok ditengah sumbu. ✓ Adanya medan vektor menyebabkan bola dapat berputar ✓ Rotasi bola mengukur curl bidang vektor F pada titik di pusat bola ✓ Medan vector F kemudian menentukan arah serta kecepatan dari bola tersebut bergerak https://mathinsight.org/curl_idea. EDUNEX ITB.

3. Curl Aliran vektor lebih kuat. Searah arah jarum jam. Berlawanan arah jarum jam. https://www.youtube.com/watch?v=rB83DpBJQsE&feature=youtu.be. EDUNEX ITB.

4. Curl. https://www.youtube.com/watch?v=rB83DpBJQsE&feature=youtu.be. EDUNEX ITB.

5. Curl. https://www.youtube.com/watch?v=qOcFJKQPZfo EDUNEX ITB.

6. Curl. https://www.youtube.com/watch?v=rB83DpBJQsE&feature=youtu.be. EDUNEX ITB.

7. Curl Fungsi Kecepatan di Sungai, yang tergantung kepada jaraknya terhadap bank. https://www.youtube.com/watch?v=vvzTEbp9lrc EDUNEX ITB.

https://www.youtube.com/watch?v=vvzTEbp9lrc. 8. Curl. Curl v=0. Curl v>0. Curl v<0. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Perhitungan Curl Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

2. Curl • Operator curl ditandai dengan simbol   serta menghasilkan fungsi vektor • Jika A = axi + a y j + azk      j + k   (a x i + a y j + a z k ) curl A =   A =  i + z  y  x i. j. k.    curl A =   A = x y z ax a y az. EDUNEX ITB.

3. Curl • Sehingga curl dari vektor A adalah sebagai berikut:  a z a y   a x a z   a y a x  i +  k curl A =   A =  − − j+ −    y   z  x   z  x  y     . • Jika   A = 0 A disebut irrotational • Curl dari gradien merupakan irrotational karena. curl (grad f ) = 0 EDUNEX ITB.

4. Curl • Contoh A = ( y 4 − x 2 z 2 )i + ( x 2 + y 2 ) j − x 2 yz k Tentukan curl A pada titik (1,3,-2) curl A =   A =. i. j. k.  x.  y.  z. y 4 − x 2 z 2 x 2 + y 2 − x 2 yz. ( ) (. ) (. ). curl A = − x 2 z i − − 2 xyz + 2 x 2 z j + 2 x − 4 y 3 k curl A = 2i − 8 j − 106 k → pada titik (1, 3, − 2). EDUNEX ITB.

5. Sifat-Sifat Curl. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Quiz Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

Quiz 4.1 • Tentukan vektor singgung satuan r(t) = 3ti +2t2j+(t2+t) k pada t=2?. EDUNEX ITB.

Quiz 4.2 • Tentukan turunan berarah dari fungsi berikut f=x2z + y2z + xz2 pada titik (1,-1,2) dan arah vektor A=4i+2j-5k. EDUNEX ITB.

Quiz 4.3 • Tentukan divergensi dari fungsi A=2x2yi – 2(xy2+y3z)j + 3y2z2k. EDUNEX ITB.

Quiz 4.4 • Tentukan curl F pada titik (2, 0, 3) F = ze 2 xy i + 2 xz cos yj + ( x + 2 y ) k. EDUNEX ITB.

Terima kasih…. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Laplace Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

6. Operator Laplace • Dalam orde yang lebih tinggi, operator del/nabla dapat dikembangkan menjadi operator Laplace, dengan persamaan berikut :           = . =  i + j + k . i + j + k  y z   x y z   x 2. 2 2  2    2 = . =  + +  x 2 y 2 z 2 .    . EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Contoh Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

Contoh Kasus • Seorang pengawas lapangan dari pembangunan runway bandara bermaksud mengecek suhu terekstrim dari sebuah campuran aspal yang dibawa dari asphalt mixing plant. Campuran tersebut di bawa menggunakan dump truk berukuran 2 m x 1,5 m x 1 m (P x L x T). Jika menganggap bahwa perubahan suhu dari campuran aspal pada dump truck tersebut mengikuti fungsi skalar berikut P2 + 2TL-2T, berikan rekomendasi kepada pengawas lapangan tersebut.. EDUNEX ITB.

Contoh kasus • Fungsi Medan Skalar :f= P2 + 2TL-2T • Anggap titik ekstrim pada saat grad f =0; • Anggap (p,t,l) ~ (x,y,z) • Maka:. • Ketika p,t,l = 0,1,0→ EDUNEX ITB.

Terima Kasihs. EDUNEX ITB.

1. Medan Skalar dan Medan Vektor. Dummy Dr. Eng. Febri Zukhruf KK Rekayasa Transportasi-FTSL. Matematika Rekayasa. EDUNEX ITB.

Vektor Kontinu • Vektor a(t) disebut kontinu di titik p jika dan hanya jika mampu memenuhi ketiga syarat berikut: (1) a( p ) terdefinisi. (2) lim a (t ) eksis t→ p. (3) lim a (t ) = a ( p ) t→ p. • Vektor a(t) disebut kontinu di set dari S, apabila vektor tersebut kontinu setiap titik pada set S EDUNEX ITB.