Kak Ajaz
Berbagi itu Berkah
2014 2015 2016
MATEMATIKA
Pembahasan Soal Ujian Nasional
Kak Ajaz
http://kakajaz.blogspot.com
PEMBAHASAN MATEMATIKA IPA UN 2014
1. Penarikan Kesimpulan
Diketahui premis-premis berikut.
Premis 1 : Jika semua pejabat negara kuat imannya maka korupsi tidak merajalela.
Premis 2 : Korupsi merajalela atau rakyat bahagia.
Premis 3 : Rakyat tidak bahagia.
Kesimpulan yang s ah dari premis-premis tersebut adal ah ...
A. Semua pejabat negara k uat imannya.
B. Semua pejabat negara tidak kuat imannya.
C. Beberapa pejabat negara tidak kuat imannya.
D. Semua pejabat negara korupsi.
E. Korupsi tidak merajalela.
Pembahasan
Soal s emacam ini tidak boleh dikerjakan dengan perasaan, tetapi harus dinalar dengan logika matematika. Kita ambil permisal an terl ebih dahulu.
p : pejabat negara kuat imanny a, q : korupsi merajalela, dan r : raky at bahagi a.
Premis 2 yang berbentuk disjungsi perlu diubah menjadi implikasi.
q ∨ r ≡ ~q ⇒ r
Kita tarik kesimpulan antara premis 1 dan 2 dulu.
Penarikan kesimpulan ini merupakan silogisme.
∀p ⇒ ~q ~q ⇒ r
∴ ∀p ⇒ r
Kesimpulan dari silogisme ini kita tarik kesimpulan lagi dengan premis 3. Penarikan kesimpul an ini merupakan modus tollens.
∀p ⇒ r
~r
∴ ~(∀p) ≡ ∃~p
Jadi, kesimpulan yang sah dari keti ga premis tersebut adal ah pernyataan "Beberapa pejabat negara tidak kuat imannya" (C).
2. Ekuivalensi
Pernyataan yang s etara dengan perny ataan "Jika suatu bilangan habis dibagi 6 maka bilangan tersebut habis dibagi 3" adalah ...
A. Jika suatu bilangan tidak habis dibagi 6 maka bilangan tersebut ti dak habis dibagi 3.
B. Jika suatu bilangan tidak habis dibagi 3 maka bilangan tersebut ti dak habis dibagi 6.
C. Jika suatu bilangan habis dibagi 3 maka bilangan tersebut habis dibagi 6.
D. Suatu bilangan habis dibagi 6 dan bilangan tersebut ti dak habis dibagi tiga.
E. Suatu bilangan habis dibagi 3 dan bilangan tersebut ti dak habis dibagi 6.
Pembahasan
Langkah pertama, kita ambil permisalan.
p : bilangan yang habis dibagi 6, q : bilangan yang habis dibagi 3.
Pernyataan yang s etara (ekuivalen) dengan implikasi adalah:
p ⇒ q ≡ ~q ⇒ ~p p ⇒ q ≡ ~p ∨ q
Berdasarkan ekuivalensi ters ebut, perny ataan yang setara dengan pernyataan di atas adalah:
Jika suatu bilangan tidak habis dibagi 3 maka bilangan tersebut ti dak habis dibagi 6.
Suatu bilangan tidak habis dibagi 6 atau bilangan tersebut habis dibagi 3.
Jadi, perny ataan y ang tepat adal ah opsi (B).
3. Perpangkatan
Bentuk sederhana dari 3𝑎−2𝑏3𝑐4 15𝑎3𝑏−5𝑐−2
−1
adal ah ....
A. 5 𝑎5
𝑏2𝑐6
B. 𝑎5𝑏2
5 𝑐6
C. 𝑐
2
5𝑎5𝑏2
D. 5 𝑎5
𝑏8𝑐6
E. 𝑎5
5𝑏8𝑐2
Pembahasan
Langkah pertama adalah menghilangkan pangkat 1.
Carany a dengan membalik bentuk pecahan ters ebut.
15𝑎3𝑏−5𝑐−2 3𝑎−2𝑏3𝑐4
Dengan bentuk seperti ini, soal tampak lebih mudah dikerjakan. Kita lebih bersemangat meny elesaikan- nya.
Selanjutnya, kumpulkan faktor-faktor yang mempunyai bilangan pokok y ang sama, bilangan pokok a dengan a, b dengan b, dan c dengan c.
Kumpulkan ke bilangan pokok yang berpangkat positif.
15𝑎3𝑎2 3𝑏3𝑏5𝑐4𝑐2
Nah, kalau bentuknya sudah seperti ini, soal tampak lebih mudah l agi. Langkah berikutnya adalah menjumlahkan pangkat dari bilangan pokok yang sama. Jangan lupa, 15 dibagi dengan 3. Hasilnya seperti ini.
5𝑎5 𝑏8𝑐6
Jadi, bentuk sederhana dari perpangkatan tersebut adal ah opsi (D).
4. Bentuk Akar
Bentuk sederhana dari 5
3 2 − 3 adal ah ....
A. 1
15 3 2 + 3 B. 1
5 3 2 + 3 C. 1
3 3 2 + 3 D. 3 3 2 + 3 E. 5 3 2 + 3
Pembahasan
Cara menyederhanakan bentuk akar pada soal tersebut adalah dengan cara mengalikan bentuk sekawan dari peny ebutny a.
5
3 2 − 3×3 2 + 3 3 2 + 3
Bagian pembilang tinggal dikalikan. Sedangkan bagi an peny ebut, gunakan rumus berikut:
𝑎 − 𝑏 𝑎 + 𝑏 = 𝑎2− 𝑏2
3 2 − 3 3 2 + 3 = 3 2 2− 3 2
= 18 − 3
= 15
Sehi ngga diperoleh:
15 2 + 5 3 15
Nah, sudah mulai mendapat titik terang. Selanjutnya, pada bagian pembilang tinggal difaktorkan dengan cara membagi masing-masing suku dengan 5.
Diperoleh:
5 3 2 + 3 15
=1
3 3 2 + 3
Jadi, bentuk sederhana dari bentuk akar tersebut adal ah opsi (C).
5. Logaritma
Hasil dari log 9
4 . log 23 + 4log 8
9log6− 9log2 adal ah ....
A. 5 B. 4 C. 3 D. 5
4
E. 3
4
Pembahasan
Soal di atas jika langsung kita kerjakan tanpa peny ederhanaan lebih dahulu akan membuat peny elesaian semakin panjang. Ini yang paling ti dak disukai siswa yang kurang minat terhadap matematika.
Baiklah, kita sederhanakan dulu beberapa bentuk log berikut:
log 9
4 =22log 32
=2
2 2log 3
= 2log 3 log 8
4 =22log 23
=2
2 2log 2
=3
2 log 6
9 − 9log 2= log6
2
9
=32log 3
=1
2
Nah, sekarang tinggal kita masukkan ke soal.
log 9
4 . log 23 + log 84
9log6 − log 29 = 2log 3. log23 + 32
1 2
=1 + 32
1 2
Kalau hasil akhi rnya sudah seperti itu, boleh dijumlah langsung. Tetapi jika i ngin lebih menikmati dalam mengerjakan soal, coba pembilang dan peny ebutnya masing-masing dikalikan 2. Hasilnya bisa membuat hati lebih tersenyum.
1 + 32
1 2
×2
2=2 + 3 1
= 5
Jadi, hasil dari bentuk logaritma ters ebut adalah 5 (A).
6. Persamaan Kuadrat
Akar-akar persamaan 𝑥2+ 𝑝 + 1 𝑥 − 18 = 0 adal ah α dan β. Jika α + 2β = 0 dan p ≥ 0, nilai p = ....
A. 0 B. 1 C. 2 D. 3 E. 4
Pembahasan
Sifat khusus akar-akar pers amaan kuadrat yang diketahui pada soal:
α + 2β = 0
α = −2β ... (1)
Sifat umum perkalian akar-akar pers amaan kuadrat.
α . β = c/a
= −18 .... (2)
Sifat umum perkalian akar-akar pers amaan kuadrat ini hukumnya wajib dihafal. Demikian juga sifat umum penjumlahan akar-akar persamaan kuadrat berikut ini.
α + β = −b/a
= −p − 1 ... (3)
Sekarang kita substi tusikan persamaan (1) ke pers amaan (2). Diperoleh:
α . β = −18
−2β . β = −18
−2β2 = −18 β2 = 9
β = ±3
Selanjutnya kita substitusikan persamaan (1) ke pers amaan (3). Diperoleh:
α + β = −p – 1
−2β + β = −p – 1
−β = −p − 1 p = β – 1
Subs titusi β = ±3 diperoleh:
p = ±3 − 1 Ini berarti :
p = 3 − 1 = 2 p = −3 − 1 = −4
Karena soal menyebutkan bahwa nilai p harus positif (p ≥ 0), maka untuk p = 4 tidak memenuhi.
Jadi, nilai p yang memenuhi pers amaan kuadrat tersebut adalah 2 (C).
7. Fungsi Kuadrat
Persamaan kuadrat 𝑥2− 𝑘 − 1 𝑥 − 𝑘 + 4 = 0 tidak mempunyai akar-akar real. Batas-batas nilai k yang memenuhi adal ah ....
A. −5 < k < 3 B. −3 < k < 5
C. k < −3 atau k > 5 D. k ≤ −3 atau k ≥ 5 E. k ≤ −5 atau k ≥ 5
Pembahasan
Tidak mempuny ai akar-akar real berarti grafiknya melayang di atas atau di bawah sumbu 𝑥. Grafikny a tidak memotong atau tidak menyinggung sumbu 𝑥.
Fungsi kuadrat seperti ini nilai diskriminannya negatif.
D < 0 b2 − 4ac < 0 (k − 1)2 − 4 . 1 . (−k + 4) < 0 k2 − 2k + 1 + 4k − 16 < 0 k2 + 2k − 15 < 0 (k + 5)(k − 3) < 0
Kalau bentuknya sudah seperti ini, kita buat garis bilangan. Jika koefisien kuadratnya positif (seperti penghi tungan di atas, koefisien k2 positif) maka di sebelah kiri dan kanan berharga positif sedangkan di tengah berharga negatif. Jika koefisien kuadratnya negatif, upayakan menjadi positif dengan mengalikan −1.
Karena pertidaks amaannya bertanda kurang dari (<) maka hasil penyeles aiannya adalah yang bertanda negatif.
Jadi, batas-batas nilai k yang memenuhi pers amaan kuadrat ters ebut adalah −5 < k < 3 (A).
8. Persamaan Linear
Rini membeli 2 kg jeruk dan 2 kg apel dengan harga Rp41. 000,00, sedangkan Ajeng membeli 4 kg jeruk dan 3 kg apel dengan harga Rp71. 000,00. Widya membeli 3 kg jeruk dan 2 kg apel pada toko yang sama. Widya membayar dengan uang Rp100.000,00.
Uang kembalian yang di terima Widy a adalah ....
A. Rp49. 000,00 B. Rp49. 500,00 C. Rp50. 000,00 D. Rp50. 500,00 E. Rp51. 000,00
Pembahasan
Soal persamaan linear itu memang mudah, tetapi butuh ketelitian dan kes abaran. Seringkali kita mengerjakannya sampai panjang lebar. Namun bila kita lebih jeli lagi, soal jenis ini memang benar-benar mudah. Kita buat permisalan terlebih dahulu. Santai saja.
𝑥 : jeruk 𝑦 : apel
Rini : 2𝑥 + 2𝑦 = 41.000 Ajeng : 4𝑥 + 3𝑦 = 71.000 Widya : 3𝑥 + 2𝑦 = ?
Umumnya, untuk mendapatkan nilai 3x + 2y, ki ta menentukan terlebih dahulu nilai x dan y-nya. Untuk soal-soal tertentu (biasanya soal UN dan SBMPTN), nilai sasaran tersebut bisa l angsung di peroleh hanya dengan s ekali eliminasi. Coba perhatikan baik -baik eliminasi berikut ini!
4𝑥 + 3𝑦 = 71.000 |× 1| 4𝑥 + 3𝑦 = 71.000 2𝑥 + 2𝑦 = 41.000 |× ½| 𝑥 + 𝑦 = 20.500 ———————— − 3x + 2y = 50.500 Karena Widy a membay ar dengan uang Rp100.000,00 maka uang kembalian yang diterima Widya adalah:
Rp100.000,00 − Rp50.500 = Rp49.500,00 Jadi, uang kembalian yang diterima Wi dya adalah Rp49. 500,00 (B).
9. Lingkaran
Salah satu persamaan garis singgung lingkaran 𝑥 − 3 2+ 𝑦 + 2 2= 5 yang sejajar garis 2𝑥 + 𝑦 = 10 adalah ....
A. 𝑦 = 2𝑥 + 1 B. 𝑦 = 2𝑥 − 1 C. 𝑦 = 2𝑥 + 9 D. 𝑦 = −2𝑥 + 9
E. 𝑦 = −2𝑥 − 11
Pembahasan
Perhatikan persamaan lingkaran dan bentuk umumny a berikut i ni!
(𝑥 − 3)2 + (y + 2)2 = 5
⇔ (𝑥 − h)2 + (y − k)2 = r2
Berdasarkan bentuk umum tersebut diperoleh data:
h = 3 k = −2 r = √5
Sedangkan pernyataan 'sejajar dengan garis' artinya mempunyai nilai gradi en y ang sama dengan garis tersebut. Mari kita tentukan gradien garis tersebut.
2𝑥 + y = 10 y = −2𝑥 + 10 ⇔ y = m𝑥 + c
Sehi ngga diperoleh nilai m = −2.
Persamaan garis singgung lingkaran dengan nilai gradien 𝑚 dirumuskan:
𝑦 − = 𝑚 𝑥 − 𝑘 ± 𝑟 𝑚2+ 1 𝑦 + 2 = −2 𝑥 − 3 ± 5 −2 2+ 1
= −2𝑥 + 6 ± 5 𝑦 = −2𝑥 + 4 ± 5
Berarti ada dua garis singgung pada lingkaran yang sejajar garis ters ebut, yaitu:
𝑦 = −2𝑥 + 4 + 5
= −2𝑥 + 9 𝑦 = −2𝑥 + 4 − 5
= −2𝑥 − 1
Jadi, salah satu persamaan garis singgung lingkaran tersebut adalah opsi (D).
10. Suku Banyak
Suku banyak berderajat 3, jika dibagi 𝑥2+ 2𝑥 − 3 bersisa (3𝑥 − 4) dan jika dibagi 𝑥2− 𝑥 − 2 bersisa (2𝑥 + 3). Suku bany ak tersebut adalah ....
A. 𝑥3− 𝑥2− 2𝑥 − 1
B. 𝑥3+ 𝑥2− 2𝑥 − 1 C. 𝑥3+ 𝑥2+ 2𝑥 − 1 D. 𝑥3+ 2𝑥2− 𝑥 − 1 E. 𝑥3+ 2𝑥2+ 𝑥 + 1
Pembahasan
Misalkan suku banyak tersebut adalah f(x). Pembagi yang pertama adalah 𝑥2+ 2𝑥 − 3 dengan sisa 3𝑥 − 4. Pembagi ini bisa difakto rkan menjadi (𝑥 + 3)(𝑥 − 1). Arti nya, untuk 𝑥 = −3 dan 𝑥 = 1 nilai f(𝑥) = 3𝑥 − 4.
f(−3) = 3(−3) − 4 = −13 f(1) = 3 . 1 − 4 = −1
Sampai di sini sebenarnya soal sudah bisa dijawab dengan cara trial and error (coba-coba pada semua opsi jawaban). Carany a, masukkan 𝑥 = −3 pada opsi jawaban kemudi an cari yang menghasilkan −13, atau gunakan angka yang lebih sederhana, yaitu 𝑥 = 1, kemudi an cari yang menghasilkan −1. Kita coba untuk 𝑥 = 1.
A. 𝑥3− 𝑥2− 2𝑥 − 1 = 1 − 1 − 2 – 1 = −3 B. 𝑥3+ 𝑥2− 2𝑥 − 1 = 1 + 1 − 2 – 1 = −1 C. 𝑥3+ 𝑥2+ 2𝑥 − 1 = 1 + 1 + 2 – 1 = 3 D. 𝑥3+ 2𝑥2− 𝑥 − 1 = 1 + 2 − 1 – 1 = 1 E. 𝑥3+ 2𝑥2+ 𝑥 + 1 = 1 + 2 + 1 + 1 = 5
Dari trial and error ters ebut, kita dapatkan jawabannya adalah B. Sekarang kita buktikan dengan cara yang semestiny a. Kita gunakan pembagi yang kedua. f(x) dibagi x2 − x − 2 sisanya 2x + 3.
Misalkan hasil baginya adal ah ax + b, diperoleh:
𝑓 𝑥 = 𝑥2− 𝑥 − 2 𝑎𝑥 + 𝑏 + 2𝑥 + 3 ... (1) Kita aplikasikan f(−3) = −13 dan f(1) = −1 pada pers amaan (1).
f(−3) = 10(−3a + b) − 3 = −13 −30a + 10b = −10 −3a + b = −1 ... (2)
f(1) = −2(a + b) + 5 = −1 −2a − 2b = −6
a + b = 3 ... (3)
Eliminasi persamaan (2) dan (3) untuk mendapatkan nilai a dan b.
−3a + b = −1 a + b = 3
————— − −4a = −4 a = 1 → b = 2
Subs titusi a = 1 dan b = 2 pada persamaan (1) diperoleh:
𝑓 𝑥 = 𝑥2− 𝑥 − 2 𝑎𝑥 + 𝑏 + 2𝑥 + 3
= 𝑥2− 𝑥 − 2 𝑥 + 2 + 2𝑥 + 3
= 𝑥3− 𝑥2− 2𝑥 + 2𝑥2− 2𝑥 − 4 + 2𝑥 + 3
= 𝑥3+ 𝑥2− 2𝑥 − 1
Jadi, jadi suku banyak berderajat 3 y ang dimaksud adal ah opsi (B).
11. Komposisi dan Invers Fungsi
Diketahui fungsi 𝑓 𝑥 = 2𝑥 + 1 dan 𝑔 𝑥 =𝑥+1
𝑥 , 𝑥 ≠ 0. Invers fungsi 𝑓 ∘ 𝑔 (𝑥) adalah 𝑓 ∘ 𝑔 −1 𝑥 = ....
A. 𝑓 ∘ 𝑔 −1 𝑥 = 2𝑥
𝑥−3, 𝑥 ≠ 3 B. 𝑓 ∘ 𝑔 −1 𝑥 = 2𝑥
𝑥+3, 𝑥 ≠ −3 C. 𝑓 ∘ 𝑔 −1 𝑥 = 2
𝑥−3, 𝑥 ≠ 3 D. 𝑓 ∘ 𝑔 −1 𝑥 = 2
𝑥+3, 𝑥 ≠ −3 E. 𝑓 ∘ 𝑔 −1 𝑥 =𝑥−3
𝑥+3, 𝑥 ≠ −3
Pembahasan
Komposisi fungsi 𝑓 ∘ 𝑔 (𝑥) biasanya dibaca "f bundaran g". Arti nya, di dalam fungsi f terkandung fungsi 𝑔 𝑥 atau fungsi 𝑔 𝑥 tersarang di dalam fungsi f.
𝑓 𝑥 = 2𝑥 + 1 𝑓 ∘ 𝑔 𝑥 = 𝑓 𝑔 𝑥
= 2𝑔 𝑥 + 1
f[g(x)] = 2g(x) + 1 mengikuti pola f(x) = 2x + 1.
Sekarang kita operasikan fungsi 𝑔 𝑥 pada komposisi fungsi tersebut.
𝑓 ∘ 𝑔 𝑥 = 2𝑔 𝑥 + 1
= 2 𝑥+1
𝑥 + 1
=2𝑥 +2
𝑥 +𝑥
𝑥
=3𝑥 +2
𝑥
Untuk menentukan fungsi inv ersnya kita gunakan rumus berikut ini.
𝑦 =𝑎𝑥 +𝑏
𝑐𝑥 +𝑑 → 𝑦−1=−𝑑𝑥 +𝑏
𝑐𝑥 −𝑎
Berdasarkan rumus ters ebut, diperoleh:
𝑓 ∘ 𝑔 𝑥 =3𝑥 +2
𝑥 +0 𝑓 ∘ 𝑔 −1 𝑥 =0𝑥 +2
𝑥 −3
= 2
𝑥 −3
Jadi, invers komposisi fungsi tersebut adalah opsi (C).
12. Persamaan Linear
Di Zedland ada dua media massa koran yang sedang mencari orang untuk bekerja sebagai penjual koran.
Iklan di bawah ini menunjukkan bagaimana mereka membayar gaji penjual koran.
Joko memutuskan untuk melamar menjadi penjual koran. Ia perlu memilih bekerja pada Medi a Zedland atau Hari an Zedl and. Grafik manakah di bawah ini yang menggambarkan bagaimana koran membay ar penjual-penjualnya?
Pembahasan
Kita ambil permisalan terlebih dahulu.
𝑥 : jumlah koran y ang terjual per mi nggu 𝑦 : pendapatan per mi nggu
Pendapatan penjual koran di Medi a Zedland:
240 koran pertama yang terjual mendapat gaji 0,2 zed per koran = 0,2𝑥.
Setelah 240, s etiap koran yang terjual mendapat gaji 0,4 zed per koran = 0,4𝑥.
Persamaan matematika pendapatan gaji di Media Zedland.
𝑦 = 0,2𝑥; 1 ≤ 𝑥 ≤ 240 0,4𝑥; 𝑥 > 240
Grafikny a terdiri dari dua garis yang berbeda kemiringan (gradien 0,2 dan 0,4) yang berawal dari pangkal koordinat (ditunjukkan oleh garis biru).
Pendapatan penjual koran di Harian Zedland.
Gaji tetap 60 zed.
Bonus 0,05 zed tiap koran terjual = 0,05x.
Persamaan matematika pendapatan gaji di Hari an Zedland.
𝑦 = 60 + 0,05𝑥
Grafikny a berupa garis lurus naik yang berawal dari 𝑦 = 60 (garis merah).
Jadi, yang menggambarkan pendapatan penjual koran di masing-masing koran adalah grafik (C).
13. Matriks
Diketahui matriks:
𝐴 = 2𝑥 −3
3 −1 , 𝐵 = 𝑥 − 𝑦 0
𝑦 + 1 3 , 𝐶 = −4 5
−3 2 Jika 𝐶𝑡 adalah transpos e dari matriks 𝐶 dan 𝐴 + 𝐵 = 𝐶𝑡, nilai dari 3𝑥 + 2𝑦 = ....
A. −1 B. −7 C. −11 D. −14 E. −25
Pembahasan
Trans pose matriks adalah matriks yang mengalami pertukaran baris menjadi kolom dan kolom menjadi baris dari matriks sebelumny a.
Jumlah koran yang terjual Pendapatan per minggu (zed)
A.
Harian Zedland
Media Zedland
Jumlah koran yang terjual Pendapatan per minggu (zed)
B.
Harian Zedland
Media Zedland
Jumlah koran yang terjual Pendapatan per minggu (zed)
D.
Harian Zedland
Media Zedland
Jumlah koran yang terjual Pendapatan per minggu (zed)
E.
Harian Zedland
Media Zedland Jumlah koran yang terjual Pendapatan per minggu (zed)
C.
Harian Zedland
Media Zedland
MEDIA ZEDLAND
PERLU UANG LEBIH?
JUAL KORAN KAMI Gaji yang akan diterima:
0,20 zed per koran sampai dengan 240 koran yang terjual per minggu, ditambah 0,40 zed per koran selebihnya yang dijual.
HARIAN ZEDLAND
DIBAYAR TINGGI DALAM WAKTU SINGKAT Jual koran Harian Zedland dan dapatkan 60 zed per minggu, ditambah bonus 0,05 per koran yang terjual.
A + B = Ct 2𝑥 −3
3 −1 + 𝑥 − 𝑦 0
𝑦 + 1 3 = −4 −3 5 2
Penjumlahan matriks adalah penjumlahan el emen- elemen matriks yang bersesuaian, kanan-atas dijumlah dengan kanan-atas, dan seterusnya.
Diperoleh:
3𝑥 − 𝑦 −3
𝑦 + 4 2 = −4 −3 5 2
Ini adalah bentuk kes amaan matriks. Seti ap elemen yang bersesuaian pada kedua matriks tersebut mempunyai nilai yang sama. Akan kita tentukan nilai 𝑥 dan 𝑦. Temukan terlebih dahulu elemen yang hany a terdiri dari satu vari abel. Ya, komponen yang terletak pada ki ri-bawah.
y + 4 = 5 y = 1
Selanjutnya kita tentukan nilai x dari komponen yang letaknya kiri-atas.
3𝑥 − 𝑦 = −4 3𝑥 − 1 = −4 3𝑥 = −3 𝑥 = −1
Dengan demikian nilai dari:
3𝑥 + 2𝑦 = 3(−1) + 2.1 = −3 + 2 = −1
Jadi, nilai dari 3𝑥 + 2𝑦 adalah −1 (A).
14. Operasi Vektor
Diketahui vektor:
𝑎 = 𝑥 2
−1
, 𝑏 = 4
−3 6
, 𝑐 = 2 0 3
Jika 𝑎 tegak lurus 𝑏 , hasil dari 3𝑎 − 𝑏 + 2𝑐 adalah ....
A.
9 0
−3
B.
9 9
−3
C.
−9 9
−3
D.
9 6 3
E.
9
−9 3
Pembahasan
Jika 𝑎 tegak lurus 𝑏 maka perkalian dot antara 𝑎 dan 𝑏 sama dengan nol.
𝑎 . 𝑏 = 0 4𝑥 − 6 − 6 = 0 4𝑥 = 12
𝑥 = 3
Sehi ngga komponen-komponen vektor 𝑎 menjadi:
𝑎 = 3 2
−1
Dengan demikian, nilai dari 3𝑎 − 𝑏 + 2𝑐 dapat ditentukan.
3𝑎 − 𝑏 + 2𝑐 = 3 3 2
−1 −
4
−3 6
+ 2 2 0 3
= 9 6
−3 −
4
−3 6
+ 4 0 6
= 9 9
−3
Jadi, hasil operasi vektor ters ebut adalah opsi (B).
15. Proyeksi Vektor
Diketahui vektor-vektor 𝑢 = −12𝑖 + 𝑎𝑗 + 𝑏𝑘 dan 𝑣 = 𝑎𝑖 − 𝑏𝑗 + 𝑎𝑘 . Sudut antara 𝑢 dan 𝑣 adalah 𝜃 dengan cos 𝜃 = 1
4 3. Proyeksi 𝑢 pada 𝑣 adalah 𝑝 = −4𝑖 + 4𝑗 − 4𝑘 . Nilai dari 𝑏 = ....
A. 4 7 B. 2 14
C. 2 7 D. 14 E. 7
Pembahasan
𝑝 adalah proyeksi 𝑢 pada 𝑣 , berarti 𝑝 searah dengan 𝑣 . Hal ini juga berarti bahwa 𝑝 merupakan kelipatan dari 𝑣 .
𝑝 = 𝑘𝑣
−4 4
−4 = 𝑘
𝑎
−𝑏 𝑎
Berdasarkan kesamaan matriks baris ke-1 dan ke-2 diperoleh:
baris ke-1 : −4 = ka 4 = −ka baris ke-2 : 4 = −kb
Sehi ngga ka = kb atau a = b.
Selanjutnya kita gunakan rumus sudut (cos θ) antara vektor 𝑢 dan 𝑣 . Sebelumnya kita tentukan dulu besaran-besaran yang diperlukan pada rumus tersebut.
Karena a = b dan yang ditanyakan b maka rumus- rumus berikut ini dinyatakan dalam b.
𝑢 = (−12, a, b)
= (−12, b, b) 𝑣 = (a, −b, a)
= (b, −b, b)
𝑢 ∙ 𝑣 = −12b − b2 + b2
= −12b
𝑢 = −12 2+ 𝑏2+ 𝑏2
= 144 + 2𝑏2 𝑣 = 𝑏2 + −𝑏 2+ 𝑏2
= 3𝑏2
= 𝑏 3
Nah, sekarang kita terapkan pada rumus sudut vektor.
cos 𝜃 = 𝑢 ∙ 𝑣 𝑢 ∙ 𝑣 3
4 = −12𝑏
144 + 2𝑏2× 𝑏 3 3 144 + 2𝑏2= −48
144 + 2𝑏2= −16
Secara matematis, soal ini kurang v alid. Hasil akar tidak mungkin negatif.
Ok, pura-pura tidak tahu. Kita kuadratkan masing- masing ruas.
144 + 2b2 = 256 2b2 = 112 b2 = 56 b = 2√14
Jadi, nilai b pada vektor tersebut adalah 2√14 (B).
16. Proyeksi Vektor
Diketahui vektor 𝑎 = 3𝑖 − 4𝑗 + 𝑝𝑘 dan 𝑏 = 2𝑖 + 2𝑗 − 3𝑘 . Jika panjang proy eksi vektor 𝑎 pada 𝑏 adal ah 4
17, nilai 𝑝 = ....
A. −2 B. −1 C. 1 D. 2 E. 3
Pembahasan
Jika panjang proyeksi vektor 𝑎 terhadap 𝑏 dinotasikan |𝑐 | maka proyeksi skalar tersebut dirumuskan:
𝑐 =𝑎 ∙ 𝑏 𝑏 4
17=6 − 8 − 3𝑝 4 + 4 + 9
Bagian penyebutnya bisa dicoret karena s ama.
Selanjutnya, tinggal mengoperasikan pembilangnya saja.
4 = 6 − 8 − 3p 4 = −2 − 3p
3p = −6 p = −2
Jadi, nilai p pada proyeksi vektor tersebut adalah 2 (A).
17. Transformasi Geometri
Persamaan bayangan lingkaran 𝑥2+ 𝑦2 = 4 bila dicerminkan terhadap garis 𝑥 = 2 dan dilanjutkan dengan translasi −3
4 adal ah ....
A. 𝑥2+ 𝑦2− 2𝑥 − 8𝑦 + 13 = 0 B. 𝑥2+ 𝑦2+ 2𝑥 − 8𝑦 + 13 = 0 C. 𝑥2+ 𝑦2− 2𝑥 + 8𝑦 + 13 = 0 D. 𝑥2+ 𝑦2+ 2𝑥 + 8𝑦 + 13 = 0 E. 𝑥2+ 𝑦2+ 8𝑥 − 2𝑦 + 13 = 0
Pembahasan
Pencerminan (refleksi) dan translasi adalah transformasi yang bersifat isometri, yaitu transformasi yang hany a mengalami perubahan posisi tanpa mengubah bentuk dan ukuran. Untuk lingkaran, yang mengalami perubahan adalah titik pusatnya sedangkan jari-jarinya tetap.
Lingkaran 𝑥2+ 𝑦2= 4 mempuny ai titik pusat P(0, 0) dan jari-jari r = 2.
Pencerminan titik pusat P(0, 0) terhadap 𝑥 = .
𝑃 𝑥, 𝑦 𝑥= 𝑃′(2 − 𝑥, 𝑦) 𝑃 0,0 𝑥 =2 𝑃′(2 × 2 − 0, 0)
𝑃′(4, 0)
Kemudian hasil pencerminan tersebut dilanjutkan dengan translasi.
𝑃 𝑥, 𝑦
𝑎
𝑃𝑏 ′(𝑥 + 𝑎, 𝑦 + 𝑏)
𝑃′ 4,0
−34
𝑃"(4 − 3, 0 + 4) 𝑃"(1, 4)
Dengan demikian, bayangan akhir ti tik pus at lingkaran ters ebut adalah (1, 4). Pers amaan lingkarannya adal ah:
(𝑥 − )2+ (𝑦 − 𝑘)2 = 𝑟2 (𝑥 − 1)2+ (𝑦 − 4)2= 4 𝑥2− 2𝑥 + 1 + 𝑦2− 8𝑥 + 16 = 4 𝑥2+ 𝑦2− 2𝑥 − 8𝑦 + 13 = 0
Jadi, persamaan bayangan lingkaran tersebut adalah opsi (A).
18. Pertidaksamaan Eksponen
Nilai 𝑥 yang memenuhi pertidaks amaan 9𝑥 − 4 ∙ 3𝑥 +1+ 27 < 0 adalah ....
A. 3 < 𝑥 < 9 B. 1 < 𝑥 < 2 C. 2 < 𝑥 < 3 D. 𝑥 < 3 atau 𝑥 > 9
E. 𝑥 < 1 atau 𝑥 > 2
Pembahasan
Langkah pertama untuk meny elesaikan soal di atas adal ah dengan menyamakan bilangan pokoknya.
9x − 4 . 3x+1 + 27 < 0 32x − 4 . 3x . 31 + 27 < 0
Selanjutnya dimisalkan 3x = p kemudi an difaktorkan.
p2 − 12p + 27 < 0 (p − 9)(p − 3) < 0
Langkah terakhi r, kita buat garis bilangan untuk menentukan daerah penyelesai annya.
Berdasarkan garis bilangan ters ebut diperoleh:
3 < p < 9 31 < 3x < 32 1 < x < 2
Jadi, nilai 𝑥 yang memenuhi pertidaksamaan tersebut adalah 1 < 𝑥 < 2 (B).
19. Pertidaksamaan Logaritma
Penyelesaian pertidaks amaan log 𝑥
2 ∙1−𝑥log 4> 2 −1−𝑥log 4 adalah ....
A. 0 < 𝑥 < 2
3
B. 0 < 𝑥 < 1
3
C. 1
3< 𝑥 <2
3
D. 1
3< 𝑥 < 1 E. 2
3< 𝑥 < 1
Pembahasan
Perhatikan bagian ruas kiri pada soal di atas!
Perkalian logari tma itu bisa ditukar, baik bilangan basis maupun numeriknya.
log 𝑥
2 ∙1−𝑥log 4
= 2log4∙1−𝑥log 𝑥
= 2 ∙1−𝑥log 𝑥
Sekarang perhatikan bagi an ruas kanan! Ubahlah 2 menjadi bentuk log 𝑎𝑎 2.
2 −1−𝑥log 4
= 1−𝑥log 1 − 𝑥 2−1−𝑥log 22
= log 1 −𝑥
2 1−𝑥 2
= 2 ∙ log 1−𝑥
2 1−𝑥
Pada bagian ruas kanan di atas, bentuk pengurangan logari tma di jadikan bentuk pembagian dengan menggunakan rumus log a − log b = log 𝑎
𝑏. Kemudian pangkat 2-nya dipindahkan ke depan berdas arkan rumus log an = n log a.
Dengan demikian, pertidaksamaan logaritma di atas dapat disederhanakan menjadi :
2 ∙ 1−𝑥log 𝑥> 2 ∙ log 1−𝑥
2 1−𝑥
Karena basis logaritmanya sudah sama, dapat disederhanakan lagi menjadi berikut ini. Jangan lupa, angka 2 di ruas kiri dan kanan dicoret dulu.
𝑥 >1−𝑥
2 2𝑥 > 1 − 𝑥 3𝑥 > 1
𝑥 >1
3
Tapi ini belum selesai. Logaritma mempunyai syarat-syarat tertentu. Tidak semua nilai dapat dilogari tmakan. Untuk menentukan syarat logari tma, perhatikan basis dan numerik logaritma pada soal, jangan pada hasil peny ederhanaan.
Syarat basis:
I. 1 − 𝑥 > 0 → 𝑥 < 1 II. 1 − 𝑥 ≠ 1 → 𝑥 ≠ 1 Syarat numerik:
𝑥 > 0
Sekarang kita buat garis bilangan. Masukan hasil penghi tungan dan syarat-syarat pada garis bilangan.
Jadi, penyeles aian pertidaksamaan logaritma tersebut adalah 1
3< 𝑥 < 1 (D).
20. Deret Aritmetika
Tempat duduk gedung pertunjukan film diatur mulai dari baris depan dengan banyak baris di belakang lebih 4 kursi dari baris di depannya. Bila dalam gedung pertunjukan terdapat 15 baris kursi dan baris terdepan ada 20 kursi, kapasitas gedung pertunjukan tersebut adalah ....
A. 1.200 kursi B. 800 kursi C. 720 kursi D. 600 kursi E. 300 kursi
Pembahasan
Ini adalah deret aritmetika yang ditandai dengan pernyataan "baris di belakang lebih 4 kursi dari baris di depanny a". Data-data yang diketahui pada soal ters ebut adalah:
b = 4 n = 15 a = 20
Sedangkan yang ditanyakan adalah bany ak seluruh kursi atau S15.
𝑆𝑛=12𝑛 2𝑎 + 𝑛 − 1 𝑏 𝑆15=12∙ 15 2 ∙ 20 + 15 − 1 4
= 720
Jadi, kapasitas gedung pertunjukan tersebut adalah 720 kursi (C).
21. Deret Geometri
Seutas tali dipotong menjadi 5 bagi an sehingga panjang potongan-potongan tali tersebut membentuk barisan geometri. Jika panjang tali
terpendek 6 cm dan potongan tali terpanjang 96 cm maka panjang tali semula adalah ....
A. 96 cm B. 185 cm
C. 186 cm D. 191 cm E. 192 cm
Pembahasan
Data y ang diketahui pada soal:
deret geometri n = 5
U1 = 6 cm U5 = 96 cm
Sedangkan yang ditanyakan pada soal adalah S5. Ki ta tentukan rasio deret geometri tersebut.
𝑟 = 𝑈5
𝑈1
5−1
= 96
6
4
= 164
= 2
Karena nilai r > 1 maka rumus jumlah deret geometri yang kita gunakan adalah:
𝑆𝑛=𝑎 𝑟𝑛−1
𝑟−1
=6 25−1
2 −1
= 6 32 − 1
= 6 × 31
= 186
Jadi, panjang tali semula adalah 186 cm (C).
22. Dimensi Tiga (jarak titik ke garis)
Diketahui kubus ABCD.EFGH dengan rusuk 9 cm.
Jika T terletak pada pertengahan garis HF, jarak titik A ke garis CT adal ah ....
A. 5 3 cm B. 6 2 cm C. 6 3 cm D. 6 6 cm E. 7 3 cm
Pembahasan
Kita gambar dulu kubusnya supaya memahami persoalannya.
Sekarang, pandanglah diagonal bidang ACGE!
Garis CT dan garis ET' adalah dua garis yang sejajar dan sama-sama menghubungkan titik tengah dan titik sudut ACGE. Dua garis ini ternyata membagi garis AG menjadi tiga bagian yang sama panjang sehingga AA' = 2
3 AG. Sedangkan AG merupakan diagonal ruang kubus ABCD.EFGH yang terkenal dengan rumus 𝑎 3 dengan 𝑎 adalah sisi kubus.
AG = 𝑎 3
= 9 3 AA' = 2
3 AG = 2
3 9 3 = 6 3
Jadi, jarak titik A ke garis CT adalah 6 3 cm (C).
23. Dimensi Tiga (sudut antara garis dan bidang)
Kubus ABCD.EFGH mempunyai rusuk 4 cm. Sudut antara AE dan bi dang AFH adalah α. Nilai sin α = ....
A. 1
2 2 B. 1
2 3 C. 1
3 3 D. 2
3 2 E. 3
4 3
Pembahasan
Perhatikan gambar berikut ini!
Untuk menentukan sudut yang dibentuk ol eh garis AE dan bidang AFH, kita tentukan dulu titik pertemuan antara garis dan bidang tersebut, yaitu titik A.
Dari titik A, ki ta tarik garis tengah bidang AFH, yai tu garis AT. Sudut yang dibentuk oleh garis AE dan garis AT inilah yang disebut sudut α.
ET adalah setengah diagonal EG. Sedangkan EG adal ah diagonal bidang kubus yang dikenal dengan rumus 𝑎 2.
EG = 𝑎 2
= 4 2 ET = 1
2 EG = 1
2× 4√2 = 2 2
Sekarang, pandanglah segitiga AET!
Segitiga AET adalah segi tiga siku-siku sehingga berlaku teorema Pythagoras dan trigonometri.
AT = AE2+ ET2
= 42+ 2 2 2
Coba masing-masing suku dalam akar dibagi 22. Diperoleh:
AT = 2 22+ 2 2
= 2 4 + 2
= 2 6
Sekarang kita tentukan nilai sinus sudutnya.
sin 𝛼 =ET
AT
=2 2
2 6
= 1
3
=1
3 3
Jadi, nilai dari sin α adalah 1
3 3 (C).
24. Trigonometri (aturan sinus dan kosinus)
Diketahui segiempat ABCD seperti gambar.
Panjang sisi BC adal ah ....
A. 7 3 cm B. 6 3 cm C. 4 5 cm D. 3 5 cm E. 2 5 cm
Pembahasan
Pandangl ah segitiga ABD!
Data pada segiti ga tersebut adalah dua sudut dan satu sisi. Karena itu, gunakan aturan sinus untuk menentukan sisi BD.
𝐵𝐷
sin 60° = 𝐴𝐷 sin 30°
𝐵𝐷
1
2 3 =2 3
1 2
Angka 12 pada masing-masing bisa dicoret kemudian dikalikan silang. Diperoleh:
BD = 2 3 × 3
= 6
Selanjutnya, pandanglah segiti ga BCD!
Karena pada segitiga tersebut diketahui satu sudut dan dua sisi, kita gunakan aturan kosinus untuk menentukan nilai BC.
BC2 = BD2 + CD2 − 2 BD . CD cos 45 = 36 + 32 − 2 6 4 2 12 2 = 20
BC = 20 = 2 5
Jadi, panjang sisi BC adalah 2 5 cm (E).
25. Trigonometri (persamaan trigonometri)
Himpunan penyel esaian dari pers amaan 2 sin 𝑥 − 3 = 0 untuk 0 ≤ 𝑥 ≤ 2𝜋 adalah ....
A. 1
3𝜋, 2
3𝜋 B. 1
3𝜋, 1
6𝜋 C. 1
3𝜋, 1
12𝜋 D. 1
3𝜋, 5
6𝜋 E. 2
3𝜋, 5
6𝜋
Pembahasan
Untuk menyelesaikan soal persamaan trigonometri, selain harus hafal sudut-s udut istimewa juga harus memperhatikan daerah atau i nterval sudut yang ditanyakan.
2 sin 𝑥 − √3 = 0 sin 𝑥 = ½ √3 sin 𝑥 = sin 60°
Pada interval 0 ≤ x ≤ 2π, nilai sin x = ½ √3 (positif) terdapat pada kuadran I dan II.
Kuadran I 𝑥 = 60°
= 60°
180°𝜋
=1
3𝜋 Kuadran II
𝑥 = 180° − 60°
= 120°
A B
C D
2 3 cm
4 2 cm
60 30
45
=120°
180°𝜋
=2
3𝜋
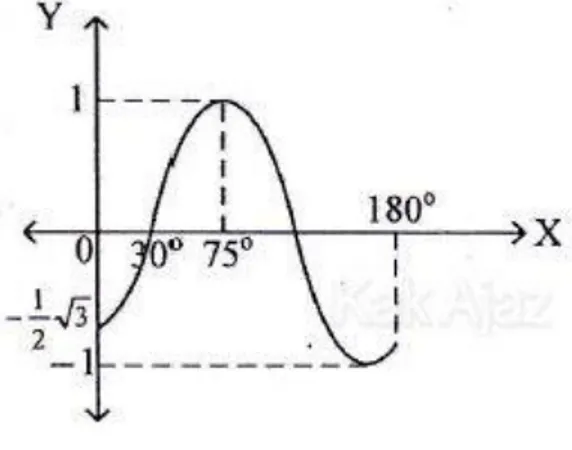
Jadi, himpunan penyelesai an dari pers amaan trigonometri tersebut adalah opsi (A).
26. Trigonometri (Rumus Jumlah dan Selisih Sinus dan Kosinus)
Nilai cos 265° − cos 95° = ....
A. −2 B. −1 C. 0 D. 1 E. 2
Pembahasan
Soal di atas dapat diselesaikan dengan menggunakan rumus jumlah dan selisih sinus dan kosinus.
cos A − cos B = −2sin ½(A+B) sin ½(A−B) Berdasarkan rumus di atas, diperol eh:
cos 265° − cos 95°
= −2 sin ½(265 + 95) sin ½(265 − 95)
= −2 sin 180° . sin 85°
= 0 (sin 180° = 0)
Jadi, Nilai dari cos 265° − cos 95° sama dengan nol (C).
27. Limit Fungsi Aljabar
Nilai dari
𝑥 →∞lim 25𝑥2+ 18𝑥 + 2 − 5𝑥 − 1 adal ah ....
A. 1 B. −2
5
C. 4
5
D. 1 E. 8
5
Pembahasan
Limit fungsi al jabar jenis ini harus diubah dulu ke bentuk:
𝑥 →∞lim 𝑎𝑥2+ 𝑏𝑥 + 𝑐 − 𝑎𝑥2+ 𝑑𝑥 + 𝑒
Hasil dari limit di atas adalah:
𝑏 − 𝑑 2 𝑎
Berdasarkan bentuk ters ebut, dapat diperoleh a = 25, b = 18, dan c = 2.
Sementara itu, nilai d dan e belum bisa kita peroleh.
Kedua nilai tersebut akan kita dapatkan s etelah melakukan sedikit manipul asi terhadap bentuk
−5𝑥 − 1.
−5𝑥 − 1 = − 5𝑥 + 1
= − 5𝑥 + 1 2
= − 25𝑥2+ 10𝑥 + 1 Sehi ngga d = 10 dan e = 1.
Dengan demikian hasilnya adalah:
𝑏 −𝑑
2 𝑎 =18 −10
2 25
= 8
10
=4
5
Jadi, nilai limit fungsi tersebut adalah ⅘ (C).
28. Limit Fungsi Trigonometri
Nilai dari lim𝑥 →0
1 − cos 2𝑥 𝑥 tan 𝑥 adal ah ....
A. −8 B. 0
C. 1 D. 2 E. 4
Pembahasan
Langkah pertama adalah mengubah bentuk kosinus menjadi sinus.
cos 2𝑥 = 1 − 2 sin2 𝑥 2 sin2 𝑥 = 1 − cos 2𝑥
Sehi ngga bentuk limit ters ebut menjadi : lim𝑥 →0
2 sin2x 𝑥 tan 𝑥
Limit fungsi trigonometri mendekati nol berlaku:
𝑥 = sin 𝑥 = tan 𝑥
Nah, sekarang ubahlah sin 𝑥 dan tan 𝑥 menjadi 𝑥 lim𝑥→0 2x2
𝑥 ∙𝑥 = 2
Jadi, nilai dari limit fungsi ters ebut adalah 2 (D).
29. Aplikasi Turunan
Diketahui fungsi 𝑔 𝑥 =1
3𝑥3− 𝐴2𝑥 + 2, dengan A = konstanta. Jika 𝑓 𝑥 = 𝑔 2𝑥 − 1 dan 𝑓 naik pada 𝑥 ≤ 0 atau 𝑥 ≥ 1, nilai minimum relatif 𝑔 adalah ....
A. −8
3
B. −4
3
C. 0 D. 4
3
E. 8
3
Pembahasan
Perhatikan pola fungsi g.
𝑔 𝑥 =1
3𝑥3− 𝐴2𝑥 + 2 𝑔 2𝑥 − 1 =1
3 2𝑥 − 1 3− 𝐴2 2𝑥 − 1 + 2 Sedangkan f adalah:
𝑓 𝑥 = 𝑔 2𝑥 − 1
=1
3 2𝑥 − 1 3− 𝐴2 2𝑥 − 1 + 2
Fungsi f naik pada 𝑥 ≤ 0 atau 𝑥 ≥ 1, artinya f' = 0 saat 𝑥 = 0 atau 𝑥 = 1. Bingung kan?
Maksudny a begini, kita diminta menurunkan fungsi f kemudi an disamadengankan nol. Setelah itu ki ta diminta melakukan subs titusi x = 0 atau x = 1 untuk mendapatkan nilai A2.
f' = 0 2(2𝑥 − 1)2 − 2A2 = 0
A2 = (2𝑥 − 1)2 𝑥 = 0 → A2 = (2.0 − 1)2 = 1 𝑥 = 1 → A2 = (2.1 − 1)2 = 1
Nilai A2 ini kita gunakan untuk mendapatkan fungsi g. Dengan melakukan s ubstitusi A2 = 1, kita peroleh fungsi g berikut ini.
𝑔 𝑥 =1
3𝑥3− 𝐴2𝑥 + 2
=1
3𝑥3− 𝑥 + 2
Nilai maksimum atau minimum terjadi saat turunan suatu fungsi sama dengan nol. Jadi, g minimum terjadi saat g' = 0.
g' = 0 𝑥2 − 1 = 0 𝑥2 = 1 𝑥 = ±1
Terdapat dua nilai 𝑥, yaitu +1 dan −1. Berarti yang satu menghasilkan g maksimum, satunya lagi menghasilkan g minimum. Mari kita periksa.
g(−1) = −⅓ + 1 + 2 = 8/3 (maksimum) g(1) = ⅓ − 1 + 2 = 4/3 (minimum)
Jadi, nilai minimum relatif fungsi g adalah 4/3 (D).
30. Integral Substitusi
Hasil dari 3𝑥 − 2
3𝑥2− 4𝑥 + 5 5 𝑑𝑥 adal ah ....
A. − 1
8 3𝑥2−4𝑥 +5 4+ C
B. − 1
4 3𝑥2−4𝑥 +5 4+ C
C. − 1
2 3𝑥2−4𝑥 +5 4+ C
D. 1
8 3 𝑥2−4𝑥 +5 4+ C
E. 1
4 3 𝑥2−4𝑥 +5 4+ C
Pembahasan
Pelan-pelan saja mengerjakan soal integral, ti dak perlu terburu-buru. Coba pindah dulu penyebutnya ke atas sehingga pangkatny a menjadi negatif.
3𝑥 − 2 3𝑥2− 4𝑥 + 5 −5 𝑑𝑥
Integral di atas mengandung dua fungsi, yaitu fungsi linear 3𝑥 − 2 dan fungsi 3𝑥2− 4𝑥 + 5 −5. Pangkat 𝑥 terti nggi dari kedua fungsi tersebut adal ah 3𝑥 dan 3𝑥2. Selisih pangkat tertingginya 2 − 1
= 1. Inilah ciri integral substitusi, selisih pangkat tertinggi nya = 1.
Prinsip integral substitusi adal ah:
𝑑𝑥 =𝑑𝑓(𝑥) 𝑓′(𝑥)
dengan 𝑓 𝑥 = 3𝑥2− 4𝑥 + 5 (dipilih karena berpangkat lebih ti nggi) dan 𝑓′ 𝑥 = 6𝑥 − 4 (turunan dari 𝑓 𝑥 ). Dengan demikian, integral di atas menjadi:
3𝑥 − 2 3𝑥2− 4𝑥 + 5 −5 𝑑𝑥 =𝑑(3𝑥2−4𝑥 +5 )
6𝑥 −4 (6𝑥 − 4) adalah 2 kali dari (3𝑥 − 2) sehingga dapat dicoret menjadi
1
2 3𝑥2− 4𝑥 + 5 −5 𝑑(3𝑥2− 4𝑥 + 5) Integral ini bentukny a sama dengan ½∫ a−5 da.
1
2 𝑎−5𝑑𝑎 =1
2∙ −1
4 𝑎−4+ C Sehi ngga diperoleh:
1
2 3𝑥2− 4𝑥 + 5 −5 𝑑(3𝑥2− 4𝑥 + 5)
=1
2∙ −1
4 3𝑥2− 4𝑥 + 5 −4+ C
= − 1
8 3 𝑥2−4𝑥 +5 4+ C
Jadi, hasil dari integral tersebut adalah opsi (A).
31. Integral Tentu Fungsi Aljabar
Nilai dari
𝑥 − 1 3𝑥 + 1
2
−1
𝑑𝑥 adal ah ....
A. −5 B. −1 C. 1 D. 2 E. 3
Pembahasan
Sebelum diintegralkan, dua faktor yang ada dalam integral tersebut dikalikan dulu, menjadi:
𝑥 − 1 3𝑥 + 1
2
−1
𝑑𝑥
= 3𝑥2− 2x − 1
2
−1
𝑑𝑥
Kalau bentuknya sudah seperti di atas, baru diintegralkan. Diperoleh:
𝑥3− 𝑥2− 𝑥 −12
Sekarang substitusikan 𝑥 = 2 dan 𝑥 = −1 per suku, seperti berikut ini.
[23 − (−1)3] − [22 − (−1)2] − [2 − (−1)]
= (8 + 1) − ( 4 − 1) − (2 + 1)
= 3
Jadi, nilai dari integral tersebut adalah 3 (E).
32. Integral Tentu Fungsi Trigonometri
Nilai dari
2 cos 3𝑥 cos 𝑥
1 4𝜋
0
𝑑𝑥 adal ah ....
A. 1
2 2 B. 1
2
C. 0 D. −1
2
E. −1
2 3
Pembahasan
Gunakan rumus perkalian sinus dan kosinus untuk mengerjakan soal di atas.
2 cos A cos B = cos (A + B) + cos (A − B) 2 cos 3𝑥 cos 𝑥 = cos 4𝑥 + cos 2𝑥 Sehi ngga bentuk integral tersebut menjadi:
cos 4𝑥 + cos 2𝑥
1 4𝜋
0
𝑑𝑥
= 1
4sin 4𝑥 +1
2sin 2𝑥
0 1 4𝜋
Hasilnya cukup dengan substitusi 𝑥 = 1
4π karena substitusi 𝑥 = 0 akan menghasilkan nol.
= 1
4 sin 4. 1
4π + 1
2 sin 2. 1
4π
= 1
4 sin 180° + 1
2 sin 90°
= 0 + 1
2
= 1
2
Jadi, nilai dari integral fungsi trigonometri tersebut adal ah 1
2 (B).
33. Integral Tak Tentu
Hasil sin34𝑥 ∙ cos 4𝑥 𝑑𝑥 = ....
A. − 1
16sin44𝑥 + C B. −1
8sin44𝑥 + C C. 1
4sin44𝑥 + C D. 1
8sin44𝑥 + C E. 1
16sin44𝑥 + C
Pembahasan
Ini adalah integral substi tusi fungsi trigonometri. dx disubstitusikan dengan d(sin 4x) karena fungsi sinus pada integral di atas berpangkat lebih tinggi dari pada fungsi kosinus. Dalam substitusi ini pangkat 3 dari fungsi sinus tidak perlu diikutkan.
sin34𝑥 ∙ cos 4𝑥 𝑑𝑥
= sin34𝑥 ∙ cos 4𝑥𝑑 sin 4𝑥 4 cos 4𝑥
=1
4 sin34𝑥 𝑑 sin 4𝑥
=1
4∙1
4sin44𝑥 + C
= 1
16sin44𝑥 + C
Jadi, tinggi hasil dari integral ters ebut adalah opsi (E).
34. Luas Daerah
Perhatikan gambar berikut ini!
Luas daerah y ang diarsir pada gambar dapat dinyatakan dengan rumus ....
A. 2𝑥08 𝑑𝑥 − 𝑥 + 4 48 𝑑𝑥 B. 2𝑥08 𝑑𝑥 + 𝑥 − 4 48 𝑑𝑥 C. 2𝑥08 𝑑𝑥 − 𝑥 + 4 48 𝑑𝑥 D. 2𝑥 − 𝑥 + 4 08 𝑑𝑥
E. 2𝑥04 𝑑𝑥 + 2𝑥 − 𝑥 + 4 48 𝑑𝑥
Pembahasan
Perhatikan gambar berikut ini!
Untuk menentukan luas daerah yang diarsir seperti gambar pada soal, kita harus membagi daerah arsiran ters ebut menjadi dua bagian. Bagi an pertama terletak pada interval 0 ≤ 𝑥 ≤ 4. Luas daerah dalam i nterval ini merupakan integral y2. Bagi an yang kedua terletak pada interv al 4 ≤ 𝑥 ≤ 8. Luas daerah dalam interval ini merupakan i ntegral y2 y1.
𝐿 = 𝐿𝐼+ 𝐿𝐼𝐼
= 𝑦2
4
0
𝑑𝑥 + 𝑦2− 𝑦1
8
4
𝑑𝑥
= 2𝑥
4
0
𝑑𝑥 + 2𝑥 − 𝑥 + 4
8
4
𝑑𝑥
Jadi, luas daerah yang diarsir dapat dinyatakan dengan rumus pada opsi (E).
35. Volume Benda Putar
Volume benda putar yang terbentuk dari daerah yang dibatasi oleh kurv a 𝑦 = − 3𝑥2, sumbu 𝑥, di dalam lingkaran 𝑥2+ 𝑦2= 4, dan diputar mengelilingi sumbu 𝑥 adalah ....
A. 80
15𝜋 satuan volume B. 68
15𝜋 satuan volume C. 64
15𝜋 satuan volume D. 34
15𝜋 satuan volume E. 32
15𝜋 satuan volume
Pembahasan
Langkah pertama adalah menentukan titik potong antara kurva dan lingkaran. Titik potong ini berguna untuk menentukan batas integrasi integral yang diinginkan. Ki ta s ubstitusikan persamaan kurva pada persamaan lingkaran.
𝑥2 + y2 = 4 𝑥2 + (− 3𝑥2)2 = 4
3𝑥4 + 𝑥2 − 4 = 0 (3𝑥2 + 4)(𝑥2 − 1) = 0 𝑥2 = −4
3 (TM) atau 𝑥2 = 1 𝑥 = ±1
TM arti nya ti dak memenuhi, hal ini karena hasil kuadrat tidak mungki n bernilai negatif. Sekarang kita perhatikan gambar berikut i ni!
2 8
2 4
𝑦 = 2𝑥 𝑥 𝑥 − 𝑦 = 4
𝑦
4
Daerah arsiran yang berwarna bi ru adalah daerah yang dibatasi oleh kurv a, sumbu 𝑥, dan lingkaran.
Daerah inilah yang akan diputar 360° terhadap sumbu x.
Coba perhatikan! Daerah sebelah kiri dan kanan sumbu y luasnya sama. Karena itu, kita cukup mengintegralkan daerah sebelah kanan saja kemudi an dikalikan 2.
Volume benda putar diperoleh dengan mengintegralkan kuadrat dari fungsi kurva dan lingkaran dengan memperhatikan interv alnya. Pada interval 0 ≤ 𝑥 ≤ 1, volume benda putar merupakan integral dari kuadrat fungsi kurva, y2 = 3𝑥4. Sedangkan pada interval 1 ≤ 𝑥 ≤ 2, volume benda putar merupakan integral dari fungsi lingkaran y2 = 4 − 𝑥2.
𝑉 = 2𝜋 3𝑥4
1
0
𝑑𝑥 + 4 − 𝑥2
2
1
𝑑𝑥
= 2𝜋 3
5𝑥5
0 1
+ 4𝑥 −1
3𝑥3
1 2
= 2𝜋 3
5 1 − 0 + 4 2 − 1 −1
3(8 − 1)
= 2𝜋 3
5+ 4 −7
3
= 2𝜋 ×34
15
=6815𝜋
Jadi, volume benda putar y ang terbentuk adalah 6815𝜋 satuan volume (B).
36. Statistika (ukuran pemusatan)
Perhatikan histogram berikut ini!
Modus data pada histogram adalah ....
A. 24,5 B. 24,9 C. 25,5 D. 25,9 E. 26,5
Pembahasan
Perhatikan gambar berikut ini!
Daerah y ang berwarna orange adalah kelas modus (yang paling tinggi). Berikut ini data-data yang berkaitan dengan kelas modus.
tb : tepi bawah kelas modus tb = 1
2 (20 + 25) = 22,5
d1 : selisih frekuensi kelas modus dengan kelas sebelumnya
d1 = 12 − 8 = 4
d2 : selisih frekuensi kelas modus dengan kelas sesudahnya
d2 = 12 − 6
= 6
i : lebar kelas i = 15 − 10 = 5
Mari kita masukkan data-data tersebut ke dalam rumus modus berikut ini.
5 10 15 20 25 30 35 40 2
4 6 8 10 12
Frekuensi
Data
𝑀𝑜 = 𝑡𝑏 + 𝑑1 𝑑1+ 𝑑2𝑖
= 22,5 + 4 4 + 6× 5
= 24,5
Jadi, modus data histogram di atas adalah 24,5 (A).
37. Statistika (ukuran letak dan penyebaran)
Berat badan 40 siswa disajikan dalam tabel distribusi frekuensi berikut ini.
Berat (kg) Frekuensi 41 – 45
46 – 50 51 – 55 56 – 60 61 – 65
5 10 14 6 5 Kuartil bawah dari data tersebut adalah ....
A. 48,0 kg B. 47,5 kg C. 47,0 kg D. 46,5 kg E. 46,0 kg
Pembahasan
Kuartil bawah terletak pada 1/4 dari jumlah seluruh data. Karena juml ah data pada soal tersebut 40, kuartil bawah terl etak pada kel as kedua. Perhatikan tabel berikut.
Data-data yang dapat diperoleh:
N = 40 f = 15 fk = 5 tb1 = 46 − 0,5 = 45,5 i = 56 − 51 = 5
Sekarang kita masukkan data-data tersebut pada rumus kuartil bawah berikut ini.
𝑄1= 𝑡𝑏1+
1 4𝑁 − 𝑓𝑘
𝑓 𝑖
= 45,5 +10 − 5 15 × 5
= 48
Jadi, kuartil bawah dari data tersebut adalah 48,0 (A).
38. Kaidah Pencacahan (perkalian)
Dari angka 1, 2, 3, 4, 5, 6, dan 7 akan disusun bilangan genap terdi ri dari 3 angka berbeda. Banyak bilangan genap yang dapat disusun adalah ....
A. 60 B. 90 C. 108 D. 120 E. 126
Pembahasan
Bilangan genap terdiri dari 3 angka artinya bilangan genap ters ebut mempunyai posisi satuan, puluhan, dan ratusan. Sedangkan yang harus bernilai genap adal ah posisi satuan.
Dari angka 1, 2, 3, 4, 5, 6, dan 7 yang harus menempati posisi satuan hany a 3 bilangan, yaitu 2, 4, dan 6. Sedangkan posisi puluhan ditempati oleh 6 dari 7 bilangan yang tersedia (karena 1 bilangan sudah menempati satuan).
Sementara itu, posisi ratus an ditempati oleh 5 bilangan (karena 2 bilangan masing-masing telah menempati s atuan dan puluhan). Dengan demikian, banyaknya bilangan genap yang tersus un adalah
3 × 6 × 5 = 90
Jadi, ada 90 bilangan genap dalam susunan tersebut (B).
39. Kaidah Pencacahan (kombinasi)
Jika setiap dua zat kimia yang berbeda dicampurkan menghasilkan zat kimia baru maka dari lima zat kimia yang berbeda dapat membentuk zat baru sebany ak ....
A. 15 B. 10 C. 8 D. 7 E. 6