HUBUNGAN ANTARA SIKAP SISWA TERHADAP MATEMATIKA DENGAN KEMAMPUAN KOMUNIKASI MATEMATIKA SISWA KELAS VIII SEMESTER I DI SMP PANGUDI LUHUR WEDI TAHUN
AJARAN 2018/2019
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Disusun Oleh: Elisabet Resti Dianingsih
141414044
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
HUBUNGAN ANTARA SIKAP SISWA TERHADAP MATEMATIKA DENGAN KEMAMPUAN KOMUNIKASI MATEMATIKA SISWA KELAS VIII SEMESTER I
DI SMP PANGUDI LUHUR WEDI TAHUN AJARAN 2018/2019
Disusun Oleh:
ELISABET RESTI DIANINGSIH NIM:141414044
Disetujui oleh
Pembimbing
iv
HALAMAN MOTTO
“Janganlah hendaknya kamu khawatir tentang apapun
juga, tetapi nyatakanlah dalam segala hal keinginanmu
kepada Allah dalam doa dan permohonan dengan ucapan
syukur”
Filipi 4:6
“kebahagiaan bukanlah sesuatu yang harus diraih. Dalam
proses
meraih sesuatu pun, kamu bisa bahagia”
RM
v
HALAMAN PERSEMBAHAN
vi
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pusaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 28 Januari 2019
Penulis
vii
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma: Nama : Elisabet Resti Dianingsih
NIM : 141414044
Dalam perkembangan ilmu pengetahuan, saya memberikan karya ilmiah saya yang berjudul:
Hubungan antara Sikap Siswa Terhadap Matematika dengan Kemampuan Komunikasi Matematika Siswa Kelas VIII di SMP Pangudi Luhur Wedi Tahun Ajaran 2018/2019 .
Dengan demikian saya memberikan hak kepada perpustakaan Universitas sanata Dharma untuk menyimpan, mengalihkan, dalam bentuk lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin saya sebagai penulis. Demikian pernyataan ini saya buat dengan sebenarnya.
Yogyakarta, 28 januari 2019 Yang menyatakan
viii ABSTRAK
Elisabet Resti Dianingsih. 141414044.2019. “Hubungan antara Sikap Siswa terhadap Matematika dengan Kemampuan Komunikasi Matematika Siswa Kelas VIII Semester 1 di SMP Pangudi Luhur Wedi Tahun Ajaran
2018/2019”. Skripsi. Program Studi Matematika. Jurusan Pendidikan
Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma Yogyakarta.
Penelitian ini bertujuan untuk mengetahui ada tidaknya hubungan positif dan signifikan antara sikap siswa terhadap matematika dan kemampuan komunikasi matematika. Penelitian ini dilaksanakan di SMP Pangudi Luhur Wedi tahun ajaran 2018/2019, pada bulan Oktober 2018.
Subyek penelitian ini adalah siswa kelas VIII SMP Pangudi Luhur Wedi. Dari populasi sebanyak 64 siswa, diambil sampel 22 dengan menggunakan teknik Purposive sampling. Data sikap siswa terhadap matematika diperoleh dari siswa yang mengisi angket sikap siswa yang dianalisis berdasarkan kriteria skor sikap siswa. Data kemampuan komunikasi matematika diperoleh dari tes kemampuan komunikasi matematika secara tertulis. Hipotesis diuji dengan menggunakan Korelasi Pearson.
Hasil penelitian menunjukan bahwa terdapat hubungan antara sikap siswa terhadap matematika dan kemampuan komunikasi matematikanya dengan koefisien relasi sebesar 0,757 dan koefisien determinan sebesar 57,3049% sedangkan sisanya adalah pengaruh faktor lain. Hasil uji korelasi menunjukan nilai = 5,183 dan ttabel=2,080.
ix ABSTRACT
Elisabet Resti Dianingsih. 1414114044.2019. “The Relation Between Students’ Attitudes Toward Mathematics And Mathematical Communication Skills On
Students Class VIII Pangudi Luhur Wedi Junior High School Academic
2018/2019. Thesis Math Education Study Program. Department Of Math
Education And Science. Faculty Of Teachers Training And Education. Sanata
Dharma University Yogyakarta.
The research aimed to find out whether there is a positive and significant relation between students’ attitude toward mathematics and mathematical communication skills. The reasearch was conducted in Pangudi Luhur Wedi Junior High School in Academic Year 2018/2019, in October 2018.
The subjects of this research were the eight grade students of Pangudi Luhur Wedi Junior High School. The population were 64 students. The samples were 22 taken by using Purposive sampling Technicque. The data of students’ attitude toward mathematics were obtained from students who filled questionaires of students's attitude which were analyzed based on the criterion of student's attitude score. The data of mathematical communication skills obtained from the result of writing test mathematical communication skills. The hypothesis was tested by using Pearson correlation.
The result of research showed that there was a positive and significant relation between students’ attitude toward mathematics and mathematical communication skills with the value of correlation coefficient 0,757 and value of determinant coefficient 57,305% while the rest was another factor. Correlation of test results showed that relation with = 5,183 and ttabel=2,080. These results demonstrated that the accepted hypotesis.
x
KATA PENGANTAR
Puji dan syukur kepada Tuhan Yesus Kristus atas berkat dan rahmat-Nya selama penulisan skripsi ini sehingga penulis dapat menyelesaikan skripsi yang berjudul “Hubungan antara Sikap Siswa terhadap Matematika dengan Kemampuan Komunikasi Matematika Siswa Kelas VIII di SMP Pangudi
Luhur Wedi Tahun Ajaran 2018/2019” dengan baik. Skripsi ini dibuat untuk
memenuhi salah satu syarat memperoleh gelar sarjana pendidikan pada Program Studi Matematika, Jurusan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.
Penulisan skripsi ini mendapatkan doa dan dukungan dari berbagai pihak. Oleh karena itu, penulis mengucapkan terimakasih kepada:
1. Bapak Dr. Yohanes Harsoyo, S.Pd., M.Si., selaku dekan Fakultas Keguruan Dan Ilmu Pendidikan Universitas Sanata Dharma.
2. Bapak Dr. M. Andy Ruditho, S.Pd., selaku ketua Jurusan Pendidikan Matematika Dan Ilmu Pengetahuan Alam Universitas Sanata Dharma. 3. Bapak Beni Utomo, M.Sc., selaku Ketua Program Studi Pendidikan
Matematika Universitas Sanata Dharma.
xi
5. Ibu Niluh Sulistyani, M.Pd., selaku dosen pembimbing yang telah dengan sabar dan teliti selama proses penyusunan skripsi ini dari awal hingga akhir.
6. Ibu Veronika Fitri Rianasari, S.Pd., M.Sc., selaku dosen yang memvalidasi serta memberikan masukan terhadap instrumen penelitian yang telah peneliti buat.
7. Kedua orang tuaku yang tercinta, Bapak Antonius Prasetyo dan Ibu Irmina Surti Irianti yang selalu mendoakan, memberikan penguatan serta kepercayaan penuh untuk setiap keputusan atau jalan yang saya ambil selama penyusunan skripsi ini.
8. Ketiga kakakku yang terkasih, Thomas Pranowo, Margaretha Indah Karnasih, dan Yosephin Asri Wulandari, beserta ketiga kakak iparku mbak Teti, Mas Anton dan Mas bayu yang selalu memberikan saran dan motivasinya dalam penyusunan skripsi.
9. Sahabat-sahabatku Titong, Awang, Ratna, Tanti, Vero, Abang, Intan, Tata, Ambar dan Olive yang telah memberikanku semangat dan dukungan untuk menyelesaikan skripsi.
10.Anak-anak kos Anggrek yang telah menemani selama 4,5 tahun ini.
11.Karya-karya Beyond the Scene (BTS) yang telah menyemangati, menginspirasi, dan menemani penulis dalam menyelesaikan skripsi ini. 12.Teman-teman pendidikan matematika angkatan 2014
xii
14.Siswa kelas VIII A dan VIII C SMP Pangudi Luhur Wedi yang telah membantu penelitian ini sebagai subyek penelitian
15.Semua pihak yang tak dapat penulis sebutkan satu per satu yang turut membantu dan mendukung penulis dalam menyelesaikan skripsi
Penulis menyadari bahwa skripsi ini jauh dari sempurna. Oleh karena itu penulis memohon maaf atas segala kekurangan yang ada dalam skripsi ini. Akhirnya, penulis berharap semoga penulisan ini dapat bermanfaat dan menjadi inspirasi bagi pembaca.
Penulis
xiii
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
HALAMAN MOTTO ... iv
HALAMAN PERSEMBAHAN ... v
PERNYATAAN KEASLIAN KARYA ... vi
PERNYATAAN PERSETUJUAN PUBLIKASI ... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xiii
DAFTAR TABEL ... xvi
DAFTAR LAMPIRAN ... xvii
BAB I PENDAHULUAN ... 1
A. Latar Belakang ... 1
B. Identifikasi Masalah ... 5
C. Rumusan Masalah ... 6
D. Batasan Masalah... 6
E. Batasan Istilah ... 6
F. Tujuan penelitian ... 7
xiv
BAB II KAJIAN TEORI ... 9
A. Hasil Belajar Siswa ... 9
B. Sikap Siswa Terhadap matematika ... 11
C. Kemampuan Komunikasi Matematika ... 17
D. Faktorisasi Suku Aljabar ... 26
E. Kerangka Berpikir ... 31
F. Hipotesis ... 33
BAB III METODOLOGI ... 34
A. Jenis Penelitian ... 34
B. Metode Peneitian ... 34
C. Lokasi dan Waktu Penelitian ... 35
D. Variabel Penelitian ... 35
E. Populasi, Sampel, dan Teknik Sampling... 35
F. Bentuk Data ... 36
G. Metode Pengumpulan Data ... 36
H. Instrumen pengumpulan Data ... 37
I. Validitas dan Realibilitas Instrumen ... 44
J. Metode Analisis Data ... 46
BAB IV HASIL DAN PEMBAHASAN ... 50
A. Persiapan dan Pelaksanaan Penelitian ... 50
B. Penyajian Data ... 57
xv
D. Pembahasan Hasil Penelitian ... 79
E. Keterbatasan Penelitian ... 83
BAB V KESIMPULAN DAN SARAN ... 84
A. Kesimpulan ... 84
B. Saran ... 85
xvi
DAFTAR TABEL
Tabel 2.1 Standar Kompetensi dan Kompetensi Dasar ... 25
Tabel 3.1 Kisi-kisi Tes Kemampuan Komunikasi Matematika ... 38
Tabel 3.2 Penskoran Setiap Pernyataan (Skala Likert) ... 39
Tabel 3.3 Kisi-kisi Angket ... 40
Tabel 3.4 Intepretasi Koefisien Korelasi ... 47
Tabel 4.1 Waktu Pengambilan Data ... 51
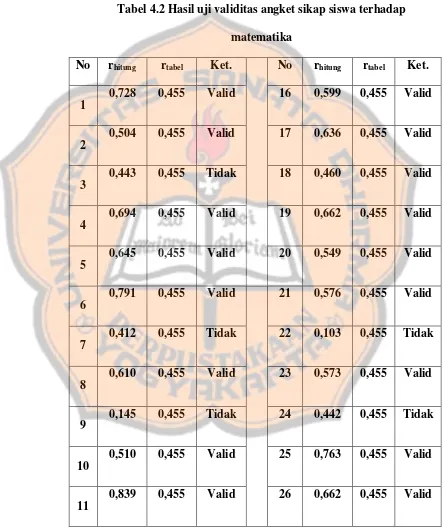
Tabel 4.2 Hasil uji validitas angket sikap siswa terhadap matematika ... 52
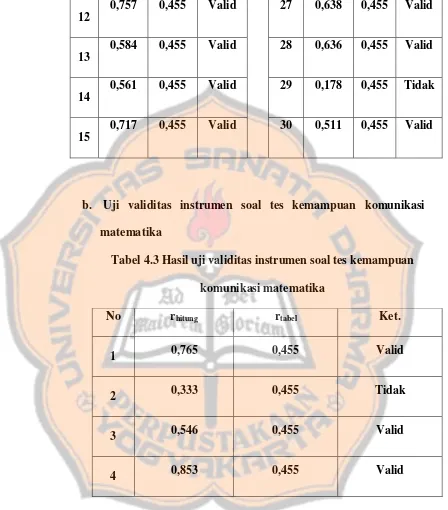
Tabel 4.3 Hasil uji validitas instrumen soal tes kemampuan komunikasi Matematika ... 53
Tabel 4.4 Hasil uji realibilitas instrumen penelitian ... 55
Tabel 4.5 Hasil pengisian angket sikap siswa terhadap matematika ... 58
Tabel 4.6 Hasil tes kemampuan komunikasi matematika ... 60
Tabel 4.7 Hasil perhitungan uji normalitas data sikap siswa terhadap Matematika ... 71
Tabel 4.8 Hasil perhitungan uji normalitas data kemampuan komunikasi Matematika ... 72
Tabel 4.9 Data perhitungan koefisien korelasi ... 73
xvii
DAFTAR LAMPIRAN
LAMPIRAN 1 Surat Penelitian ... 91
LAMPIRAN 2 Lembar Validasi Instrumen ... 93
LAMPIRAN 3 Instrumen Angket ... 100
LAMPIRAN 4 Instrumen Kemampuan Komunikasi Matematika ... 105
LAMPIRAN 5 Data Uji Validitas Dan Realibilitas Instrumen Angket ... 115
LAMPIRAN 6 Data Uji Validitas Dan Realibilitas Instrumen Tes ... 118
LAMPIRAN 7 Hasil Uji Normalitas SPSS ... 120
LAMPIRAN 8 Hasil Uji Hipotesis SPSS ... 122
1 BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Matematika merupakan salah satu mata pelajaran yang wajib dikuasi oleh pelajar. Salah satu peran matematika ialah sebagai bahasa simbolik yang memungkinkan komunikasi secara cermat dan tepat. Hal tersebut sesuai dengan tujuan umum pembelajaran matematika yang dirumuskan oleh NCTM (National Countil of teacher of Mathematic) yaitu mencakup kemampuan pemecahan masalah, kemampuan komunikasi, kemampuan koneksi, kemampuan penalaran dan representasi. Sebagai suatu bahasa, pelajar diharapkan dapat menggunakannya untuk mengkomunikasikan informasi maupun ide-ide yang diperolehnya. Komunikasi yang dimaksud dapat berupa lisan maupun tulisan dimana persoalan disampaikan melalui bahasa matematika, misalnya dengan menyajikan suatu permasalahan kedalam model matematika berupa grafik, diagram, persamaan matematika, tabel dan lain-lain.
Guerreiro (2008), “Komunikasi matematika merupakan alat bantu dalam transmisi pengetahuan matematika atau sebagai pondasi dalam
membangun pengetahuan matematika”. Oleh karena itu, komunikasi matematika sebagai bagian dari hasil belajar matematika dapat dijadikan dasar atau pondasi bagi siswa untuk belajar matematika ditahapan selanjutnya. Keterampilan mengekspresikan tersebut serta pengetahuan yang diperolehnya dari hasil belajar sebelumnya dapat digunakan untuk meningkatkan kemampuannya dalam mengekspresikan suatu persoalan matematika.
Dalam merealisasikan upaya peningkatan kemampuan komunikasi matematika tersebut memang bukanlah hal yang mudah. Menurut penuturan dari guru pengampu matematika Di SMP Pangudi Luhur Wedi, pengembangan komunikasi matematika terkadang tidak maksimal mengingat bahwa waktu penyelesaian materi memiliki tuntutan untuk segera diselesaikan. Pengajar merasa kekurangan waktu untuk mengembangkan kemampuan ketrampilan dalam pengekspresian ide yang dimiliki siswa jika harus semua ditumpuk dalam satu semester. Menurut beliau, kendala tersebut harus diimbangi dengan kemauan siswa sendiri belajar diluar jam belajar sekolah.
dirinya. Syah (2003:144) menyatakan bahwa faktor yang mempengaruhi belajar siswa dari dalam diri siswa secara psikologis yaitu: tingkat kecerdasan, intelegensi, sikap, minat, bakat, motivasi, kemampuan menghubungkan konsep-konsep, perkembangan mental dan faktor yang bersifat jasmani. Sikap seorang siswa terhadap suatu pembelajaran matematika baik berupa penolakan maupun penerimaan akan berpengaruh terhadap hasil belajarnya.
Penolakan maupun penerimaan yang ditunjukan oleh siswa saat pembelajaran matematika berlangsung tentunya akan berpengaruh terhadap hasil yang diinginkan oleh pengajar dalam mencapai tujuan pembelajarannya. Ruseffendi (1997: 9-12) mengemukakan bahwa satu diantara 5 hal yang mempengaruhi keberhasilan belajar siswa adalah sikap positif siswa. Sikap siswa terhadap matematika dan komunikasi matematis adalah suatu hal yang perlu diperhatikan baik diawal maupun selama proses pembelajaran matematika berlangsung. Jika demikian maka tidak menutup kemungkinan sikap siswa terhadap matematika juga berkaitan dengan kemampuan komunikasi matematis.
siswa. Anak-anak yang berada pada tingkatan kelas VIII diyakini telah mengalami penyesuaian belajar di sekolah tersebut, sehingga dalam tuntutanya untuk menghadapi pembelajaran matematika selanjutnya, pemahaman akan kemampuan-kemampuan yang dimiliki baik hasil dari belajar maupun beberapa faktor belajar hasil belajar sebelumnya menarik untuk diketahui.
Saat melakukan kunjungan pertama di SMP Pangudi Luhur wedi, guru pengampu mata pelajaran matematika mengatakan bahwa dalam pengamatannya selama mengajar, ia menemukan bahwa karakter yang beragam dalam belajar matematika. Pilihan yang tepat digunakan pada awal pembelajaran adalah mengetahui hal mendasar yang dimiliki siswa. Salah satu pengukuran dasar yang dapat dilakukan yakni sikap siswa terhadap matematika dan kemampuan komunikasi matematika.
apabila terjadi peningkatan pada sikap siswa terhadap matematika maka kemampuan komunikasi matematikanya akan meningkat juga.
Untuk menjawab kebenaran pernyataan yang ada di atas, peneliti merasa tertarik untuk mengetahui hubungan antara sikap siswa terhadap matematika dengan kemampuan komunikasi matematika di SMP Pangudi Luhur Wedi. Maka peneliti mengambil judul karya tulis “Hubungan Antara Sikap Siswa terhadap Matematika dengan Kemampuan Komunikasi Matematika Siswa Kelas VIII Semester I di SMP
Pangudi Luhur Wedi Tahun Ajaran 2018/2019”
B. Identifikasi Masalah
Berdasarkan latar belakang di atas dapat diidentifikasi permasalahan sebagai berikut:
1. Sikap siswa terhadap matematika yang menjadi dasar bagi siswa dalam merespon pembelajaran sering diabaikan meskipun berdampak pada hasil belajar.
C. Rumusan Masalah
Berdasarkan uraian latar belakang dan identifikasi masalah di atas, maka dapat dikemukakan rumusan masalah berikut:
“Apakah ada hubungan yang positif dan signifikan antara sikap siswa terhadap matematika dengan kemampuan komunikasi matematika siswa kelas VIII semester I di SMP Pangudi Luhur Wedi tahun ajaran 2018/2019?”
D. Batasan Masalah
Agar pembahasan tidak terlalu meluas maka dalam penelitian ini hanya mencakup materi pembelajaran matematika dengan pokok bahasan faktorisasi aljabar. Kesimpulan dari penelitian ini tidak dapat digunakan untuk sekolah lain maupun tahun ajaran lain. Pengukuran kemampuan komunikasi matematika dilakukan secara tertulis dengan data pendukung yakni wawancara guru dan siswa.
E. Batasan Istilah
1. Sikap siswa dalam matematika adalah kecenderungan menolak atau menerima matematika berdasarkan penilaian matematika sebagai hal yang berharga untuk diri sendiri.
2. Kemampuan komunikasi matematika adalah suatu keterampilan penting dalam matematika yaitu kemampuan untuk mengekspresikan ide-ide matematika secara koheran kepada teman, guru dan lainnya melalui bahasa lisan ataupun tulisan. Melihat dari definisi komunikasi, maka penelitiini lebih mengarah pada komunikasi secara tulisan dimana pelajar mampu menuliskan tentang apa yang mereka kerjakan, mampu mengklarifikasi ide-ide, membuat argumen yang meyakinkan disaat menghadapi persoalan matematika. Sebab inti dari menulis adalah komunikasi, karena dengan menulis kita sedang menyampaikan pesan untuk orang lain dan untuk diri sendiri.
F. Tujuan Penelitian
G. Manfaat Penelitian
Penelitian ini diharapkan dapat bermanfaat bagi:
1. Guru Matematika dalam upaya untuk meningkatkan pengetahuan matematika yakni dengan meningkatkan kemampuan komunikasi matematika melalui pengubahan cara pandang ataupun pemberian respon siswa terhadap matematika, ataupun sebaliknya meningkatkan kemampuan komunikasi memperbaiki sikap siswa terhadap matematika selama pembelajaran. Hal ini dimaksudkan untuk membantu siswa dapat mencapai tujuan belajarnya.
9 BAB II
KAJIAN TEORI
A. Hasil Belajar Siswa
Ada berbagai pengertian belajar yang dikenal dan dijadikan pedoman dalam kegiatan pembelajaran. Menurut Burton (Susanto, 2013:3), belajar dapat diartikan sebagai perubahan tingkah laku pada diri individu berkat adanya interaksi antara individu dengan individu lain dan individu dengan lingkungannya sehingga mereka lebih mampu berinteraksi dengan lingkungannya. Sementara menurut Hilgard (1962), belajar adalah suatu perbahan kegiatan reaksi terhadap lingkungan. Perubahan kegiatan yang dimaksud mencakup pengetahuan, kecakapan, tingkah laku, dan ini diperoleh melalui latihan (pengalaman). Hilgard menegaskan bahwa belajar merupakan proses mencari ilmu yang terjadi dalam diri seseorang melalui latihan, pembiasaan, pengalaman dan sebagainya.
materi pelajaran tertentu (Brahim dalam Susanto, 2015:5). Kegiatan pembelajaran atau kegiatan instruksional, biasanya guru menetapkan tujuan belajar. Anak yang berhasil dalam belajarnya adalah yang berhasil mencapai tujuan-tujuan pembelajaran atau tujuan instruksional.
Terdapat dua faktor yang dapat mempengaruhi proses belajar dan hasil belajar siswa yakni, faktor internal dan faktor eksternal. Kedua faktor sangatlah memiliki pengaruh yang beragam dan berbeda untuk setiap siswa. Menurut Syah (2003:144), faktor internal yang mempengaruhi belajar siswa (faktor psikologis) yaitu: tingkat kecerdasan, intelegensi siswa, sikap siswa, minat, bakat, motivasi, kemampuan yang menghubungkan konsep-konsep, perkembangan mental, dan sebagainya. Sedangkan secara eksternal faktor yang mempengaruhi belajar siswa meliputi lingkungan sekolah, lingkungan keluarga, tempat tinggal keadaan teman sebaya, fasilitas belajar, dan waktu belajar.
B. Sikap Siswa Terhadap Matematika 1. Pengertian Sikap
Sikap berasal dari bahasa latin “aptus” yang berarti dalam
keadaan sehat dan siap melakukan aksi/tindakan. Secara harafiah, sikap dipandang dalam kesiapan raga yang dapat diamati. Banyak pengertian dari kata sikap seperti yang akan dijabarkan berikut ini oleh beberapa ahli, yaitu:
a. Menurut W.S Winkel (1987:228), Sikap berarti kecenderungan untuk menerima atau menolak suatu obyek berdasarkan penilaian terhadap obyek itu sebagai hal yang berguna atau berharga (sikap positif) atau tidak berguna atau tidak berharga (sikap negatif). b. Menurut Bimo (2003), sikap adalah keyakinan seseorang tentang
suatu objek atau situasi yang relatif tetap dan teratur disertai adanya adanya perasaan tertentu dan memberikan dasar untuk merespon dengan cara tertentu yang dipilihnya.
c. Menurut Kamus Besar Bahasa Indonesia (2018), sikap adalah perbuatan dan sebagainya yang berdasarkan pada pendirian, keyakinan.
d. Notoatmodjo (1993) menyatakan bahwa sikap merupakan kesiapan atau kesediaan seseorang untuk bertindak.
kegiatan individu yang bersangkutan dalam memberikan respon dalam obyek atau situasi yang memberi arti baginya.
Dari definisi-definisi yang dikemukakan di atas dapat disimpulkan bahwa sikap merupakan sebuah kecenderungan yang dimiliki seorang individu dalam memberikan respon pada obyek sikap tertentu baik berupa penolakan (negatif) maupun penerimaan (positif) sesuai dengan penilaian akan obyek tersebut bagi dirinya. Pada dasarnya sikap bukan merupakan suatu pembawaan, melainkan hasil interaksi antara individu dengan lingkungan sehingga sifat bersifat dinamis. Sikap tidaklah terbentuk dengan sendirinya, karena pembentukan sikap senantiasa akan berlangsung dalam interaksi manusia berkenaan dengan obyek tertentu (Dayakisni, 2009:82).
2. Komponen Sikap
pengetahuan, pandangan, keyakinan yaitu hal-hal yang berhubungan dengan bagaimana orang mempersepsi terhadap obyek sikap (Bimo, 2003:107). Faktor yang membentuk kepercayaan tersebut adalah pengalaman pribadi maupun yang diceritakan orang lain, dan kebutuhan emosional.
Komponen afektif merupakan perasaan yang menyangkut hubungan emosional seseorang terhadap obyek sikap. Reaksi emosional ini dipengaruhi oleh kepercayaan seseorang terhadap obyek tersebut. Dengan lebih sederhana kita dapat mengatakan bahwa komponen afektif merupakan komponen yang berhubungan dengan rasa senang atau tidak senang terhadap suatu obyek sikap (Bimo, 2003:108). Jika kita percaya bahwa sesuatu sangat sulit dilakukan maka kita akan mulai tidak menyukai hal tersebut begitu pula sebaliknya. Peranan emosi menjadi akar dari sikap seseorang terhadap obyek tertentu.
beberapa macam respon yang digunakan oleh peneliti dalam mengukur sikap yaitu:
a. Respon bersifat kognitif
Respon bersifat kognitif berhubungan dengan pemikiran atau persepsi kita tentang objek sikap. Obyek sikap tersebut dapat berupa benda, orang, institusi social maupun peristiwa tertentu. Secara verbal, pemikiran seseorang dapat diidentifikasi dari ungkapan keyakinan (beliefs) atas sesuatu, baik yang cenderung negative maupun positif. Keyakinan ini berkaitan dengan pengetahuan, pemahaman, dan konsepsi seseorang terhadap obyek tersebut.
b. Respon bersifat afektif
Respon bersifat afektif yang menunjukan sikap seseorang dapat kita simpulkan dari evaluasi atau perasaan seseorang atas obyek dari sikapnya. Secara verbal kita dapat memperolehnya dari apakah ia mencela atau memuji, menaruh hormat atau membenci, dan lain sebagainya. Dapat dikatakan pula bahwa respon yang bersifat afektif merupakan perasaan yang menyangkut hubungan emosional seseorang terhadap obyek sikap.
c. Respon bersifat konatif
menemukannya dengan memperhatikan apa yang dikatakan seseorang tentang apa yang dikerjakan, direncanakan atau yang akan mereka lakukan seandainya berada disituasi tertentu. Respon ini juga berkaitan dengan komponen perilaku yang merupakan salah satu aspek dari sikap, di mana komponen yang dimaksudkan menunjukan bagaimana perilaku atau kecenderungan yang ada dalam diri saat berhadapan dengan salah satu obyek sikap. Oleh karena itu, sikap sikap siswa terhadap suatu obyek tercemin pada prilakunya terhadap obyek tersebut.
seberapa positif atau negatif sikap yang dimiliki seseorang terhadap suatu obyek.
3. Sikap Siswa terhadap Matematika
Sikap siswa terhadap matematika mempengaruhi prestasi belajar matematika dan prestasi yang dicapai berpengaruh pula pada pembentukan sikap siswa terhadap matematika (Primasiwi, 2012). Sikap siswa menjadi salah satu faktor internal yang mempengaruhi siswa belajar. Dalam bidang studi matematika, sikap siswa terhadap matematika dapat diketahui dari respon kognitif, afektif maupun konatif siswa tersebut terhadap matematika. Selain itu juga sikap siswa terhadap matematika dapat dilihat dari kemauannya untuk terlibat atau melibatkan diri dalam berbagai kegiatan yang berkaitan dengan matematika.
menjadi faktor dasar yang mempengaruhi belajar siswa. Sikap merupakan sebuah kecenderungan, maka jika hal tersebut negatif akan membawa hasil yang kurang memuaskan bagi pembelajaran matematika diakibatkan kurangnya keterlibatan siswa yang secara senang hati untuk mengikuti pembelajaran yang berlangsung.
C. Kemampuan Komunikasi Matematika
Komunikasi merupakan kegiatan yang dapat kita temukan disekitar kita. Pengertian komunikasi banyak dikemukakan oleh beberapa ahli yang kemudian dapat dijadikan acuan maupun pedoman yang digunakan oleh beberapa orang untuk mengungkap pengerttian dari komunikasi. Aristoteles yang hidup empat abad sebelum masehi dalam bukunya Rethoric (Ansari, 2016:11) membuat definisi komunikasi dengan menekankan “siapa mengatakan apa kepada siapa”. Selanjutnya definisi
ini dikembangkan oleh ahli ilmu politik bernama Lasswel pada tahun 1948 yaitu “siapa yang mengatakan apa, melalui apa, kepada siapa, dan apa
akibatnya” (Cangra, 2007).
Pernyataan tersebut ingin mengatakan bahwa komunikasi adalah suatu proses di mana individu menyampaikan seseuatu secara verbal kepada orang lain dengan tujuan merubah tingkah laku pendengarnya. Ada pengertian berbeda dari komunikasi yang di sampaikan oleh Bareleson, Steiner, dan Gerbner pada tahun 1964 (Ansari, 2016:12) yakni mereka mengatakan bahwa komunikasi tidak hanya sebatas verbal melainkan dapat juga menggunakan simbol-simbol, kata-kata, grafik dan lain-lain yang sejenis.
Dalam ilmu komunikasi terdapat tiga bentuk komunikasi yaitu komunikasi linier (satu arah), komunikasi “relational & interaktif” dan
komunikasi konvergen (multi arah). Konsep komunikasi konvergen merupakan prinsip pertama dalam pengajaran dan pembelajaran. Di dalam pengertiannya komunikasi konvergen merupakan komunikasi yang berlangsung secara multi arah, diantara penerima menuju suatu fokus atau minat yang dipahami bersama dan berlangsung secara dinamis serta berkembang kearah pemahaman kolektif dan berkesinambungan (Ansari, 2016:13). Sedemikian hingga dalam hal pengajaran dan pembelajaran berarti bahwa keberhasilan program belajar-mengajar salah satunya bergantung pada bentuk komunikasi yang digunakan oleh guru pada saat ia berinteraksi dengan siswa, siswa kepada guru maupun antar siswa. Dalam matematika komunikasi ditujukan pada pemecahan masalah.
Disisi lain kita mengetahui bahwa matematika memiliki peran sebagai “bahasa” simbolik yang memungkinkan terwujudnya komunikasi
Akan tetapi selain pengertian bahwa matematika sebagai alat komunikasi, ada juga pengertian komunikasi matematika atau komunikasi dalam matematika (communication in mathematic). Komunikasi dalam matematika berkaitan dengan kemampuan dan keterampilan siswa dalam berkomunikasi. Menurut Guerreiro (2008), komunikasi matematika merupakan alat bantu dalam transmisi pengetahuan matematika atau sebagai pondasi dalam membangun matematika.
Menurut Armiati (2003: MP-18), “Komunikasi matematika adalah suatu keterampilan penting dalam matematika yaitu kemampuan untuk mengekspresikan ide-ide matematika secara koheran kepada teman, guru dan lainnya melalui bahasa lisan ataupun tulisan”. Dengan menggunakan
Komunikasi matematika adalah suatu kegiatan yang melibatkan cara menafsirkan dan menyatakan gagasan matematika baik secara lisan maupun tulisan, sedangkan kemampuan komunikasi matematika adalah kecakapan atau kesanggupan siswa dalam melakukan kegiatan yang melibatkan penafsiran dan menyatakan gagasan secara lisan maupun tulisan. Menurut Sumarmo (Sari, 2016: 2), kemampuan komunikasi matematika merupakan salah satu dari lima kemampuan dasar dalam mempelajari matematika. Hal itu menjadikan bahwa pengetahuan seorang pengajar tentang kemampuan komunikasi matematika siswa yang diajarnya penting untuk diketahui untuk mempelancar proses pembelajaran. Adapun pengertian dari kemampuan komunikasi matematika yaitu kemampuan siswa untuk mempresentasikan dan menjelaskan suatu pemecahan masalah atau ide matematika dengan menggunakan simbol-simbol matematika, tabel, diagram, gambar, grafik dalam pemecahan masalah matematis.
Pada penelitian ini kemampuan komunikasi matematika yang diamati hanyalah kemampuan komunikasi matematika secara tertulis. Menurut Sumarmo (Endriani, 2017: 4), kemampuan komunikasi matematis meliputi kemampuan:
a. Menghubungkan benda nyata, gambar dan dan diagram kedalam ide matematis
c. Menyatakan peristiwa sehari-hari dalam bahasa atau symbol matematis d. Mendengarkan, berdiskusi dan menulis tentang matematika
e. Membaca dengan pemahaman atau presentasi matematika tertulis f. Membuat konjektur, menyusun argumen, merumuskan definisi, dan
generalisasi
g. Menjelaskan dan membuat pernyataan tentang matematika yang dipelajari
Kemampuan komunikasi matematika tersebut dapat diketahui secara tertulis setelah pemberian skor terhadap kemampuan siswa dalam menjawab soal-soal komunikasi matematika. Pemberian skor kemampuan komunikasi matematika siswa didasarkan pada efektivitas, ketepatan, dan ketelitian siswa dalam menggunakan bahasa matematika seperti model matematika, simbol, tanda, atau representasi untuk menjelaskan operasi, konsep dan proses. Menurut Ansari (2016), komunikasi matematika tulisan adalah kemampuan menggunakan kosa kata (vocabulary), notasi, struktur matematika untuk menyatakan hubungan dan gagasan serta memahaminya dalam pemecahan masalah. Kemampuan ini diungkapkan melalui representasi matematika. Representasi matematika siswa diklarifikasi dalam tiga kategori yaitu:
a. Pemunculan model konseptual seperti gambar diagram, tabel, dan grafik (aspek drawing)
c. Argumentasi verbal yang didasari pada analisis terhadap gambar dan konsep-konsep (aspek writen texts).
Berdasarkan ketiga kategori tersebut maka terdapat tiga aspek yang dapat digunakan untuk mengukur kemampuan komunikasi matematika (Nisa, 2012), antara lain sebagai berikut:
1) Aspek I : “kemampuan memberikan alasan rasional terhadap suatu pernyataan”.
Aspek ini merujuk kepada kategori ketiga dalam kemampuan komunikasi matematika. Berdasarkan kategori tersebut aspek yang diukur yakni bagaimana siswa dapat menuliskan argumentasi yang didasari pada gambar, konsep-konsep dalam penyelesaian masalah matematika. Menurut Syah (2003:120), pada umumnya siswa yang berikir secara rasional akan menggunkan prinsip-prinsip dan dasar-dasar pengertian dalam menjawab pertanyaan “bagaimana” (how) dan “mengapa” (why). Dalam berpikir rasional siswa dituntut
menggunakan logika (akal sehat) untuk menentukan sebab akibat, menganalisis, bahkan menciptakan hukum-hukum dan dugaan-dugaan.
2) Aspek II : “kemampuan mengubah bentuk uraian ke dalam model matematika”.
notasi matematika lainnya. Dengan demikian yang termasuk kemampuan dalam aspek ini adalah kemampuan dalam hal memodelkan suatu permasalahan kedalam kalimat matematika kemudian menyelesaikannya. Pada aspek kedua pengukuran didasarkan pada kategori kedua dimana siswa dapat terampil menuliskan penyelesaian suatu persoalan matematika ke dalam model matematika.
3) Aspek III : “kemampuan mengilustrasikan ide-ide matematika kedalam bentuk representasi yang relevan”.
Kemampuan yang coba diukur pada aspek ini berdasarkan kategori komunikasi matematika yang pertama, dimana siswa dapat terampil memunculkan model konseptual seperti gambar diagram, tabel, dan grafik (aspek drawing). Sementara kemampuan mengemukakan ide dalam teks dengan benar dalam teks dengan benar secara lisan maupun tulisan menggunakan bahasa sendiri, dapat membantu seorang siswa memahami teks tersebut secara bermakna.
Kemampuan komunikasi matematis tidak bersifat statis sehingga dapat dikembangkan. Beberapa faktor yang dapat mempengaruhi kemampuan komunikasi matematika adalah sebagai berikut (Ansari, 2016:33-41): a. Pengetahuan prasyarat (prior knowledge)
siswa tentu saja bervariasi sesuai dengan kemampuan siswa itu sendiri. jenis kemampuan yang dimiliki oleh siswa tersebut sangat menentukan hasil pembelajaran selanjutnya.
b. Kemampuan membaca, diskusi, dan menulis
Kemampuan siswa dalam hal membaca, diskusi, dan menulis juga dapat mempengaruhi kemampuan komunikasi matematika siswa yakni dalam komunikasi matematika yang dilakukannya untuk memperjelas pemikiran mereka dan mempertajam pemahaman. Ketiga kemampuan tersebut membantu siswa dalam mengelaborasi topik-topik, menyimpulkan sebuah topik-topik, pengenalan kembali informasi dan struktur melalui membaca, mengemukakan pendapat, dan menemukan strategi.
c. Pemahaman matematika (mathematical knowledge)
Istilah pemahaman berbeda menurut siapa yang memahami sesuatu dan apa yang dipahami. Membantu siswa dalam meningkatkan pemahaman dalam matematika berarti meminta mereka membangun jaringan representasi mental. Yang dimaksud sebagai pemahaman matematika disini adalah tingkat atau level pengetahuan siswa tentang konsep, prinsip, algoritma, dan kemahiran siswa menggunakan strategi penyelesaian terhadap soal yang diberikan.
matematika yang dimiliki siswa sebagai hasil belajarnya terdahulu merupakan kemampuan dasar yang digunakan oleh siswa dalam menerima pembelajaran matematika.
D. Faktorisasi Suku Aljabar
Materi tentang faktorisasi suku aljabar diajarkan di kelas VIII pada semester I. Berdasarkan Kurikulum Tingkat Satuan Pendidikan (KTSP), materi ini memiliki standar kompetensi dan kompetensi belajar (Depdiknas, 2006) yaitu:
Tabel 2.1 Standar Kompetensi dan Kompetensi Dasar
Standar Kompetensi Kompetensi Dasar
Aljabar
1. Memahami bentuk aljabar, relasi, fungsi dan persamaan garis lurus
1.1 Melakukan operasi aljabar
2.1 Menguraikan bentuk aljabar ke dalam faktor-faktornya
Berikut ini adalah beberapa materi yang digunakan oleh peneliti dalam membuat instrumen tes kemampuan komunikasi matematika (Marsigit, 2009:3-20) yaitu:
1. Operasi penjumlahan dan pengurangan bentuk aljabar
Operasi penjumlahan dan pengurangan bentuk aljabar dapat dilakukan pada suku-suku sejenis. Ada beberapa sifat yang berlaku pada penjumlahan dan pengurangan bentuk aljabar, yaitu:
Jika a dan b adalah bentuk aljabar maka pada penjumlahan berlaku sifat komutatif , sedangkan pada pengurangan tidak berlaku sifat komutatif
b. Sifat asosiatif
Jika a,b dan c merupakan bentuk aljabar maka pada penjumlahan berlaku ( ) ( )
c. Sifat distributif
Jika a,b, dan c merupakan bentuk aljabar maka berlaku: 1) Sifat distributif penjumlahan ( ) 2) Sifat distributif pengurangan ( ) 2. Operasi perkalian pada bentuk aljabar
a. Perkalian suatu bilangan dengan suku dua
Perkalian suatu bilangan dengan suku dua dapat diselesaikan dengan menggunakan sifat distributif perkalian terhadap penjumlahan atau pengurangan.
1) Jika ( ) adalah suku dua, maka
( ) (sifat distributif pada penjumlahan)
2) Jika ( ) adalah suku dua, maka
( ) (sifat distributif pada pengurangan)
b. Perkalian suku dua dengan suku dua
Sifat-sifat distributif dapat digunakan untuk menjabarkan perkalian suku dua, yakni sebagai berikut:
=
Contoh:
( )( ) ( ) ( )
( )( )
2) ( )( ) ( ) ( ) =
Contoh:
( )( ) ( ) ( )
3) ( )( ) ( ) ( ) =
Contoh:
( )( ) ( ) ( )
( )( )
3. Pemfaktoran suku aljabar
Pemfaktoran bentuk bentuk dan dapat dilakukan dengan menggunkan sifat distributif perkalian terhadap penjumlahan atau pengurangan bentuk aljabar. Suku-suku yang memiliki faktor yang sama dapat difaktorkan sebagai berikut:
( )
( )
b. Faktorisasi bentuk
Pemfaktoran bentuk akan menghasilkan suatu bentuk kuadrat. Cara pemfaktoran dari bentuk di atas dapat dipahami sebagai berikut:
1) Faktorisasi dari bentuk
( ) ( )
( )( )
( )
2) Faktorisasi dari bentuk
( ) ( )
( )( )
( )
c. Faktorisasi bentuk selisih dua aljabar
( )( )
d) Setelah melakukan langkah (c) kamu akan memperoleh ( ) ( )
( )( )
Dengan dan ( ) ( ) e. Menyederhanakan pecahan bentuk aljabar
E. Kerangka Berpikir
Sebuah keberhasilan pembelajaran salah satunya dapat dilihat dari hasil belajarnya di sekolah. Seperti yang dinyatakan oleh K. Brahim (Susanto, 2013:5) hasil belajar dapat diartikan sebagai tingkat keberhasilan siswa dalam mempelajari materi pelajaran disekolah berupa skor yang diperoleh melalui tes mengenai sejumlah materi pelajaran tertentu. Salah satu keberhasilan belajar menurut NCTM, yaitu adanya kemampuan komunikasi matematika. Di mana kemampuan ini dapat menjadi dasar seorang siswa mempelajari matematika.
Selain kemampuan belajar, salah satu faktor internal dasar yang mempengaruhi belajar yakni sikap. Sikap siswa terhadap matematika menentukan bagaimana pandangan siswa dalam menanggapi pembelajaran matematika apakah ia menolak ataupun menerima dengan baik kegiatan belajar-mengajar dalam bidang studi matematika. Adanya sikap yang lebih cenderung positif terhadap matematika maka akan berdampak baik dalam hasil belajarnya, demikian sebaliknya (Primasiwi, 2012). Suka ataupun tidak sukanya siswa terhadap matematika menentukan bagaimana siswa itu bersikap dalam memberikan respon penolakan ataupun penerimaan yang pastinya berdampak pada mau atau tidaknya ia mempelajari matematika dengan sungguh-sungguh.
keduanya saling berkaitan. Kemampuan komunikasi matematika dipandang sebagai salah satu hasil belajar yang dapat digunakan untuk pembelajaran selanjutnya, dengan demikian sikap yang tertanam dalam siswa terhadap matematika dapat memiliki hubungan signifikan terhadap kemampuan komunikasi matematika siswa.
Peneliti akan mengukur kedua hal tersebut untuk mengetahui apakah terdapat hubungan yang signifikan antara sikap siswa terhadap kemampuan komunikasi matematika. Hasil dari penelitian ini akan membantu guru matematika untuk memilih strategi yang baik dalam pembelajaran. Sikap positif siswa terhadap matematika dapat berdampak pada kemampuan komunikasi matematika, diamana ia dapat dengan senang hati mengembangkan diri dalam menyampaikan ide atau pemikirannya dalam memecahkan masalah matematika. Sebaliknya sikap siswa terhadap matematika yang negatif akan membuat siswa memiliki kemampuan komunikasi siswa yang rendah dalam memecahkan masalah matematika.
Sikap siswa terhadap matematika
F. Hipothesis
Berdasarkan penjelasan yang diuraikan di atas maka dapat diajukan hipotesis sebagi berikut:
“Terdapat hubungan positif dan signifikan antara sikap siswa terhadap
34 BAB III
METODOLOGI
A. Jenis Penelitian
Penelitian ini merupakan penelitian asosiatif/hubungan. Tujuan dari penelitian asosiatif/hubungan adalah mengetahui hubungan antara dua variabel atau lebih. Dengan penelitian ini maka akan dibangun suatu teori yang dapat berfungsi untuk menjelaskan, meramalkan dan mengontrol suatu gejala (Siregar, 2014: 7).
B. Metode Penelitian
C. Lokasi dan Waktu Penelitian
Penelitian ini dilaksanakan di SMP Pangudi Luhur Wedi selama bulan Maret 2018 hingga Januari 2019. Pelaksanaan uji coba instrumen dan pengambilan data penelitian dilakukan pada 02-10 Oktober 2018.
D. Variabel Penelitian
Dalam penelitian ini terdapat dua variabel yaitu variabel (X) yakni sikap siswa terhadap matematika dan variabel (Y) yakni kemampuan komunikasi matematika.
E. Populasi, Sampel, dan Teknik Sampling
Populasi adalah seluruh data yang menjadi perhatian peneliti dalam suatu ruang lingkup, dan waktu yang sudah di tentukan (Kasmadi, 2013:65). Populasi dalam penelitian ini adalah seluruh siswa kelas VIII SMP Pangudi Luhur Wedi tahun ajaran 2018/2019. Jumlah populasi yang sebanyak 64 siswa. Sedangkan, sampel adalah sebagian dari jumlah dan karakteristik yang dimiliki oleh populasi tersebut. Penelitian ini menggunakan sebanyak 22 siswa kelas VIII A sebagai sampel.
dimana teknik penentuan sampel dengan pertimbangan tertentu (Sugiyono, 2014: 125-126).
F. Bentuk Data
Dalam penelitian ini bentuk data pengukuran sikap dan data kemampuan komunikasi matematika yang digunakan adalah data kuantitatif. Data kuantitatif adalah data berupa angka. Sesuai dengan bentuknya, data kuantitatif dapat diolah atau dianalisis dengan menggunakan teknik perhitungan statistik. Data kuantitatif yang digunakan berupa data dikotomi, yakni data dalam bentuk bilangan bulat atau pecahan yang diperoleh dari hasil pengukurn serta tergantung dengan jenis skala pengukuran yang digunakan (Siregar, 2014:17).
G. Metode Pengumpulan data
Pengumpulan data adalah suatu prosedur yang sistematis dan standar untuk memperoleh data yang diperlukan, sehingga dalam penelitian ini metode penggumpulan data yang digunakan adalah (Siregar, 2014:18-22).
1. Penyebaran Kuesioner (Angket)
2. Tes
Menurut Kasmadi (2013) dalam bukunya menyatakan tes merupakan rangkaian pernyataan yang memerlukan testi sebagai alat ukur dalam proses asesmen maupun evaluasi dan mempunyai peran peting untuk mengukur pengetahuan, keterampilan, bakat atau kemampuan yang dimiliki individu atau kelompok. Dalam penelitian ini jenis tes yang dipakai ialah tes kemampuan komunikasi matematika.
3. Wawancara
Wawancara adalah proses memperoleh keterangan/data untuk tujuan penelitian dengan cara tanya jawab, sambil bertatap muka antara pewawancara dengan seorang responden dengan alat yang dinamakan panduan wawancara. Hal ini digunakan guna mencegah kekeliruan dalam memperoleh data dan informasi yang diperlukan dalam penelitian
H. Instrumen Pengumpulan data
1. Soal Tes
Instrumen tes yang digunakan yakni dalam bentuk tes uraian. Tes dilakukan oleh peneliti untuk mengukur kemampuan komunikasi matematika berdasarkan :
1. Materi : Faktorisasi suku aljabar
Standar kompetensi : 1. Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis lurus
Kompetensi dasar : 1.1 Melakukan operasi aljabar
1.2 Menguraikan bentuk aljabar kedalam faktor-faktornya
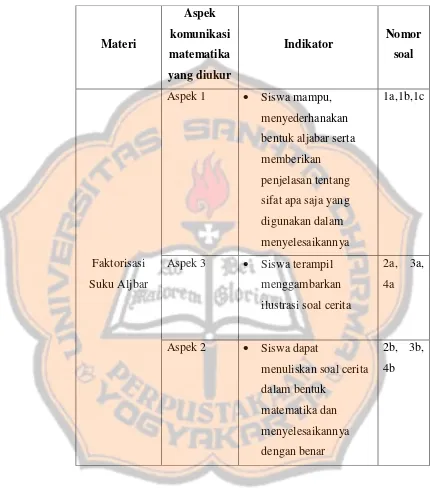
2. Aspek pengukuran kemampuan komunikasi matematika meliputi: Aspek I : “Kemampuan memberikan alasan rasional
terhadap suatu pernyataan”.
Aspek II : “Kemampuan mengubah bentuk uraian ke dalam model matematika”.
Aspek III : “Kemampuan mengilustrasikan ide-ide matematika kedalam bentuk representasi yang relevan”.
Tabel 3.1 Kisi-kisi Tes Kemampuan Komunikasi Matematika
2. Non tes
Angket sebagai suatu teknik pengumpulan data yang merupakan sebuah bentuk teknik komunikasi tidak langsung. Pengisian angket diisi sebaik-baiknya sesuai dengan keadaan sebenarnya yang dialami subjek penelitian. Angket pengukuran sikap siswa terhadap matematika berisikan 30 butir pernyataan.
Peneliti memilih menyusun kuesioner menggunakan skala likert dalam bentuk checklist untuk memudahkan peneliti saat mengolah data. Data yang didapat dari kuesioner berupa data interval atau rasio. Hal ini berdasarkan pendapat Sugiyono (2014:134), yang menyatakan bahwa skala likert merupakan salah satu dari empat jenis skala sikap yang dapat digunakan dalam pengukuran yakni berupa data interval atau rasio.
Tiap pernyataan pada kuesioner ini memiliki lima tingkat jawaban yaitu Sangat Setuju (SS), Setuju (S), Tidak setuju (TS), Sangat Tidak Setuju (STS). Pemberian skor untuk tiap-tiap pertanyaan adalah sebagai berikut:
Tabel 3.2 Penskoran Setiap Pernyataan (Skala Likert)
Pilihan Sikap
+ -
Sangat Setuju (SS) 4 1
Setuju (S) 3 2
Tidak Setuju (TS) 2 3
Skala sikap yang digunakan dalam penelitian ini diadaptasi dari skala sikap yang dikembangkan oleh Yunika Primasiwi dengan penambahan dan pengubahan tertentu sesuai dengan apa yang diteliti oleh peneliti. Skala yang digunakan berisikan tentang pandangan siswa terhadap matematika baik penolakan, penerimaan, peranan dan fungsi matematika serta pemahaman tentang matematika berdasarkan komponen sikap.
Dibawah ini akan disajikan indikator pengukuran sikap siswa terhadap matematika yang akan disajikan dalam bentu tabel, yakni:
Tabel 3.3 Kisi-kisi Angket
Komponen
Sikap Indikator Angket Favorable
dengan perasaan
JUMLAH BUTIR KUESIONER 30
b. Wawancara
Beberapa komponen wawancara yang berkaitan dengan permasalahan peneliti antara lain:
Untuk siswa:
a) Mengetahui kemampuan komunikasi matematika 2 anak dengan kategori kemampuan komunikasi matematika tinggi dan 2 anak dalam kategori rendah secara lisan
b) Mengetahui letak kelebihan dan kekurangan keempat anak tersebut mengenai pemahaman soal
c) Mengetahui pendapat keempat anak terhadap matematika d) Faktor yang mempengaruhi kemampuan komunikasi
matematika
Untuk guru pengampu matematika:
a) Mengetahui tentang keberagaman jenis tingkat kemampuan komunikasi matematika siswa
b) Mengetahui bagaimana pembelajaran matematika dikelas c) Mengetahui pendapat guru tersebut akan sikap yang ditunjukan
oleh siswa terkait pelajaran matematika
d) Mengetahui pendapat guru tentang hubungan antara sikap siswa terhadap matematika dengan kemampuan komunikasi matematika
I. Validitas dan Realibilitas Instrumen
Instrumen yang baik harus valid dan reliabel. Maka dari itu beberapa isntrumen yang digunakan dalam penelitian akan diuji validitas dan realibilitasnya, yakni kuesioner, dan soal tes kemampuan komunikasi matematika. Uji yang digunakan adalah validasi isi, validasi butir, dan realibilitasnya.
Validitas adalah suatu ukuran yang menunjukan tingkat-tingkat kevalidan atau kesahihan suatu instrumen (Arikunto, 2006:168). Dalam penelitian ini akan digunakan pengujian validasi isi dimana untuk menguji validitas butir-butir dikonsultasikan dengan ahli, maka selanjutnya diujicobakan, dan dianalisis dengan pengujian analisis item (validasi butir item), yaitu mengkorelasikan skor tiap butir instrumen dengan skor total yang merupakan jumlah tiap skor butir (Sugiyono, 2018:181). Maka dari itu teknik yang digunakan dalam oleh peneliti dalam penelitian ini adalah teknik korelasi product moment dari Pearson (Arikunto, 2013:85), dan rumus yang digunakan adalah sebagai berikut:
∑ (∑ )(∑ )
√ ( ) (∑ ) √ ( ) (∑ )
Keterangan:
n : Jumlah responden X : Skor item
Y : Skor total
Setelah koefisien korelasi ( ) ditemukan, maka akan diuji dengan
product moment tabel ( ) pada taraf signifikan 5% dan n. Jika
maka dapat dikatakan bahwa alat ukur atau butir instrumen itu valid dan dapat digunakan untuk penelitian.
Dalam validitas, instrumen dituntut valid menyangkut harapan diperoleh data yang valid, sesuai dengan kenyataan. Dalam hal realibilitas tuntutan yang dinginkan tidak jauh berbeda. Jika validitas menyangkut ketepatan objek yang tidak lain adalah tidak menyimpangnya data dari kenyataan, artinya data itu benar, maka konsep reliabilitas terkait dengan pemotretan berkali-kali. Instrumen yang baik adalah instrumen yang dapat digunakan sesuai dengan perubahan (dapat dipercaya). Suatu instrument yang reliable dan dapat dipercaya maka akan menghasilkan data yang dipercaya juga. Dalam penelitian ini, yang digunakan untuk mengetes realibilitas instrumen adalah rumus Alpha (Arikunto, 2013:122), yakn sebagai berikut:
( ) ( ∑ ∑ )
Keterangan:
n = Banyaknya soal
Setelah nilai realibilitas ( ) ditemukan, maka akan diuji dengan
product moment tabel ( ) pada taraf signifikan 5% dan n. Jika
maka dapat dikatakan bahwa alat ukur atau butir instrumen itu reliabel dan dapat digunakan untuk penelitian. Selain itu juga dapat dilihat dari kategori berikut ini, yakni:
: Sangat Tinggi
: Tinggi : Cukup : Rendah : Sangat Rendah
J. Metode Analisis Data
Variabel X : sikap siswa terhadap matematika Variabel Y : Kemampuan komunikasi matematika Koreasi bermanfaat untuk mengukur kekuatan hubungan antara dua variabel atau lebih dengan skala tertentu yang di ukur dengan jarak 0 sampai dengan 1. Pengukuran statistik asosiasi dua variabel atau kovariasi disebut dengan koefisien variasi dan jika tidak sama dengan nol, berarti terdapat hubungan antara dua variabel tersebut. Hubungan dikatakan korelasi atau hubungan sempurna jika koefisien korelasi +1 dengan kemiringan (slope) positif atau dengan kemiringan negatif. Untuk koefisien korelasi sempurna, tidak perlukan hipotesis karena variabel X memiliki hubungan yang sangat kuat dengan variabel Y.
Teknik yang akan digunakan dalam analisis ini adalah teknik korelasi pearson product moment. Uji korelasi pearson digunakan untuk menguji hipotesis asosiatif dengan data interval atau rasio yang berdistribusi normal. Teknik analisis data yang digunakan meliputi: 1. Uji asumsi
a. Uji Normalitas
2. Koefisien korelasi
Koefisien korelasi adalah bilangan yang menyatakan kekuatan hubungan antara dua variabel atau lebih atau juga dapat menentukan arah dari kedua variabel. Nilai korelasi ( ) ( ) dengan interpretasi sebagai berikut:
Tabel 3.4 Intepretasi Koefisien Korelasi Interval koefisien Tingkat hubungan 0,00 – 0,199 Sangat Rendah
Analisis yang dilakukan dengan cara perhitungan manual dan juga dengan bantuan SPSS for Windows versi 20,0. Ada tidaknya korelasi diantara variabel-variabel penelitian akan dilihat dari taraf signifikan 5%. Langkah-langkah pengujian yang dilakukan dalam penelitian ini adalah:
a. Merumuskan dan
: Tidak terdapat hubungan positif dan signifikan antara sikap siswa terhadap matematika dengan kemampuan komunikasi matematika dikalangan para siswa kelas VIII SMP Pangudi Luhur Wedi tahun ajaran 2018/2019”
antara sikap siswa terhadap matematika dengan kemampuan komunikasi matematika dikalangan para siswa kelas VIII SMP Pangudi Luhur Wedi tahun ajaran 2018/2019”
b. Hipotesis statistik
c. Taraf signifikan d. Daerah kritis
e. Menentukan nilai statistik uji D:
√ √
f. Membuat kesimpulan
Tolak ditolak jika dan dapat disimpulkan bahwa
50 BAB IV
HASIL DAN PEMBAHASAN
A. Persiapan Dan Pelakasanaan Penelitian 1. Persiapan penelitian
Persiapan penelitian dimulai dengan pengajuan surat ijin penelitian dari pihak universitas yang akan ditujukan kepada sekolah yang menjadi tempat pelaksanaan penelitian. Perijinan penelitian dilakukan pada tanggal 2 agustus 2018. Lokasi yang digunakan dalam penelitian yaitu di SMP Pangudi Luhur Wedi yang terletak di Karangrejo, Pendes, Wedi, Klaten. Peneliti mendapatkan ijin setelah melalui pembicaraan bersama kepala sekolah serta guru pelajaran matematika di hari itu juga.
Setelah itu, peneliti mencari informasi mengenai kondisi sikap siswa terhadap matematika dan kemampuan komunikasi matematika serta pemilihan kelas yang tepat digunakan untuk penelitian berdasarkan keterangan secara lisan yang diungkapkan oleh guru matapelajaran matematika di sekolah itu, yakni ibu Ch. Retno Prasetyaningsih, S.Pd. Melalui pembicaraan tersebut disepakati bahwa pelaksanaan uji coba instrumen akan dilaksanakan di kelas VIII C dan pengambilan data penelitian dilaksanakan di kelas VIII A.
kemampuan komunikasi matematika. Penyusunan butir angket dan pembuatan soal tes berpedoman pada kajian pustaka yang ada pada bab sebelumnya, yakni bab 2. Selanjutnya instrumen penelitian di validasi oleh dosen pendidikan matematika.
Kesimpulan dari hasil validasi angket sikap siswa terhadap matematika adalah angket Layak Digunakan (LD). Sedangkan. Untuk instrumen tes kemampuan komunikasi matematika mendapatkan kesimpulan bahwa soal Layak Digunakan dengan Revisi (LDR). Setelah melakukan revisi, instrumen penelitian digunakan untuk uji coba. Berikut ini adalah jawal yang digunakan oleh peneliti dalam melakukan penelitian.
Tabel 4.1 Waktu Pengambilan Data
No Kegiatan Waktu
1 Uji coba instrumen penelitian di kelas VIII C
Selasa, 2 Oktober 2018
2 Pengambilan data penelitian di Kelas VIII A
Kamis, 4 Oktober 2018
2. Hasil uji validitas instrumen
a. Uji validitas instrumen angket sikap sisa terhadap matematika Tabel 4.2 Hasil uji validitas angket sikap siswa terhadap
12
0,757 0,455 Valid 27 0,638 0,455 Valid
13
0,584 0,455 Valid 28 0,636 0,455 Valid
14
0,561 0,455 Valid 29 0,178 0,455 Tidak
15
0,717 0,455 Valid 30 0,511 0,455 Valid
b. Uji validitas instrumen soal tes kemampuan komunikasi matematika
Tabel 4.3 Hasil uji validitas instrumen soal tes kemampuan komunikasi matematika
No rhitung rtabel Ket.
1 0,765 0,455 Valid
2 0,333 0,455 Tidak
3 0,546 0,455 Valid
4 0,853 0,455 Valid
penggunaan instrumen penelitian berdasarkan panduan dari US Departemen of Labor, dalam buku Azwar (2018). Dalam buku tersebut diungkapkan bahwa, tidaklah realitis untuk berharap bahwa memperoleh koefisien validitas skor yang sangat tinggi mendekati sempurna. Cronbach mengatakan bahwa umumnya jika nilai r tabel kurang lebih atau mendekati 0,500 maka akan baik maka dalam rentang 0,300-0,500 butir instrumen dapat dianggap baik pula dengan pertimbangan rentang sangat berguna, dapat berguna, 0,11-0,20 tergantung keadaan, dan koefisien validitas masuk dalam kategori tidak dapat digunakan. Dengan demikian, dalam memberikan intepretasi dalam membuat keputusan untuk menerima validitas skor perlu disetrai pertimbangan mengenai tujuan atau fungsi skor yang diperoleh, ukuran sample, seberapa kritis makna skor bagi subyek yang akan di tes dan pertimbangan-pertimbangan lain yang relevan. (Azwar, 2009:149-150).
komunikasi matematika karena rhitung yang hampir mendekati rtabel untuk perhitungan validasi soal nomor 3 maka dengan melakukan beberapa revisi maka instrumen baru bisa digunakan. Setelah memperbaiki beberapa item yang tidak valid tersebut, peneliti akhirnya mendapatkan instrumen yang dapat dipakai dalam pengambilan data. Hasil pengolahan rhitung uji validitas menggunakan microsoft excel 2010 selengkapnya dapat dilihat pada lampiran.
3. Hasil uji realibilitas intrumen
Berikut ini adalah rangkuman hasi uji realibilitas instrumen yaitu instrumen angket sikap siswa terhadap matematika dan instrumen soal tes kemampuan komunikasi matematika siswa kelas VIII SMP Pangudi Luhur Wedi.
Tabel 4.4 Hasil uji realibilitas instrumen penelitian No Variabel rhitung rtabel Ket.
1
Sikap 0,944 0,455 Reliabel
2
Tes 0,468 0,455 Reliabel
dengan nilai r hitung sebesar 0,468. Dari data tersebut maka ketiga variabel tersebut dapat digunakan dalam penelitian.
4. Pelaksanaan Penelitian
a. Pengumpulan data angket dan tes komunikasi matematika Pengumpulan data dilaksanakan pada:
Hari,tanggal : Kamis, 4 Oktober 2018 Waktu : Jam pelajaran ke-6 dan ke-7
Kelas : VIII A
Pengumpulan data oleh peneliti dilakukan selama 120 menit. Pembagian waktu yang digunakan yakni 100 menit untuk mengerrjakan soal tes kemampuan komunikasi matematika dan 20 menit selanjutnya yakni mengisi angket sikap siswa terhadap matematika. Pengambilan data dilaksanakan pada 22 Siswa kelas VIII SMP Pangudi Luhur wedi.
b. Pengambilan data melalui wawancara Pengumpulan data dilaksanakan pada:
Hari,tanggal : Rabu, 4 Oktober 2018 Waktu : 09.00 – 10.45 WIB Narasumber :
1) Guru matematika kelas VIII, 2) S1 ( siswa satu),
Pelaksanaan wawancara dilakukan setelah hasil tes kemampuan komunikasi dan hasil angket sikap siswa terhadap matematika ada. Wawancara melibatkan guru matematika untuk mengetahui informasi dan pengonfirmasian terkait keadaan anak didik di kelas serta mengenai keseharian dari 2 anak yang memiliki hasil tes tertinggi (S1,S2) dan 2 anak dengan hasil tes terendah (S3,S4). Wawancara ini bertujuan untuk mengkonfirmasikan data penelitian, dan mencari informasi terkait dengan adakah faktor lain yang mungkin mempengaruhi.
B. Penyajian Data
Setelah pelaksanaan penelitian, diperoleh data-data yang akan dianalisis. Data tersebut akan diuraikan sebagai berikut:
1. Data hasil pengisian angket sikap siswa terhadap matematika
58 Tabel 4.5 Hasil pengisian angket sikap siswa terhadap matematika
DATA PENELITIAN
Jumlah NO. ANGKET
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
A1 2 3 3 3 2 4 3 3 4 3 3 2 3 2 2 2 3 2 3 2 3 2 2 2 2 2 1 2 2 3 75
A2 2 2 4 3 2 1 4 2 3 3 3 4 4 3 3 3 3 3 3 3 3 2 3 4 3 2 3 2 3 2 85
A3 2 3 3 2 2 3 4 2 3 4 2 3 3 2 2 2 4 2 3 4 4 3 2 4 2 3 2 2 2 2 81
A4 4 3 3 4 3 3 4 4 3 3 4 4 4 4 4 4 1 4 2 4 4 4 4 3 4 4 3 4 3 4 106
A5 2 2 3 1 2 3 3 2 2 2 2 2 3 3 3 3 3 2 2 3 2 2 3 2 2 2 1 2 2 3 69
A6 2 4 3 2 4 4 3 2 3 2 3 4 4 3 4 3 2 1 3 4 3 3 3 1 2 2 2 3 3 3 85
A7 3 3 3 2 3 3 4 3 3 3 2 3 2 3 3 3 3 3 3 2 3 3 3 3 2 3 3 3 2 3 85
A8 3 4 4 3 2 3 3 3 3 3 3 2 2 3 2 2 2 3 2 3 3 4 3 3 3 3 3 3 3 2 85
A9 2 3 3 2 3 3 3 2 3 3 2 2 3 2 3 3 3 3 3 3 3 3 3 3 2 2 2 3 2 3 80
A10 3 4 3 3 2 2 4 3 3 3 3 3 4 2 2 3 4 3 3 4 4 3 3 2 3 3 3 4 2 4 92
59
A12 2 2 4 2 1 2 2 3 2 2 2 2 3 4 2 3 4 3 3 3 4 1 1 2 3 2 3 4 3 3 77
A13 1 3 2 2 3 2 4 2 2 2 2 1 3 3 2 3 2 2 3 3 4 2 2 2 2 1 2 2 1 3 68
A14 2 2 3 2 3 3 3 2 3 2 2 3 3 2 3 3 2 3 2 3 2 3 2 3 2 2 3 3 2 3 76
A15 2 4 2 1 2 3 3 3 3 3 2 2 2 3 3 3 3 3 3 4 3 3 2 3 2 2 3 3 3 3 81
A16 3 3 2 2 1 2 3 3 3 1 2 3 3 3 3 3 3 3 4 4 3 3 4 2 1 3 2 3 1 2 78
A17 2 3 3 2 3 3 3 2 2 3 3 3 3 2 3 3 3 3 2 3 3 3 3 3 2 2 3 2 3 2 80
A18 1 3 3 1 2 3 3 1 2 2 1 1 4 2 3 3 2 3 1 4 4 3 1 2 1 1 2 1 2 2 64
A19 2 4 3 2 2 3 3 2 3 3 2 3 3 3 3 2 3 2 3 3 3 3 2 2 2 2 2 3 3 3 79
A20 3 3 2 2 1 3 2 3 3 1 2 4 4 3 2 3 1 4 2 3 2 2 3 1 2 3 3 3 2 2 74
A21 3 2 2 2 2 3 1 3 3 2 3 3 2 3 3 2 3 2 2 2 3 3 3 3 3 3 3 2 2 3 76
2. Data hasil tes kemampuan komunikasi matematika
Pengambilan data tes kemampuan komunikasi matematika dilaksanakan kamis, 04 Oktober 2018 oleh 22 siswa kelas VIII SMP Pangudi Luhur Wedi. Soal yang digunakan dalam tes berbentuk soal uraian. Jumlah soal 4 butir dan waktu pengerjaan 90 menit. Materi yang digunakan meliputi faktorisasi aljabar. Nilai kemampuan komunikasi matematika diperoleh dengan perhitungan, yakni:
Hasil dari perhitungan dibulatkan hingga pembulatan terakhir. Berikut ini akan disajikan data hasil tes kemampuan komunikasi matematika:
Tabel 4.6Hasil tes kemampuan komunikasi matematika
A15 8 10 5 0 23 26
A16 0 0 17 10 27 30
A17 12 10 5 1 28 31
A18 0 1 6 3 10 11
A19 9 5 0 0 14 16
A20 4 3 5 1 13 14
A21 0 5 8 5 18 20
A22 2 7 4 1 14 17
3. Data hasil wawancara
Wawancara dilakukan oleh peneliti pada tanggal 10 Oktober 2018, dilakukan pada 5 narasumber, yakni guru matematika kelas VIII, dua siswa dengan hasil tes komunikasi matematika tertinggi dan dua siswa dengan hasil tes kemampuan komunikasi matematika terendah. Wawancara yang dilakukan bersifat bebas terpimpin. Wawancara dalam penelitian ini bersifat sebagai pendukung dalam pengumpulan data penelitian. Wawancara dilakukan untuk memperkuat informasi yang telah diperoleh dari angket dan hasil tes. Berikut ini adalah hasil wawancara yang telah dilakukan oleh peneliti:
a. Hasil wawancara dengan dua siswa yang mendapatkan nilai tes komunikasi matematika tertinggi (S1 dan S2)
1) Mengetahui pendapatnya tentang kemampuan komunikasi matematika yang dimilikinya