Integration Danang Mursita

Integration

• The Indefinite Integral

• The Definite Integral

• The Fundamental Theorem of Calculus

• Application of Integration : Area between two

curves

• Definition : A function F(x) is called an antiderivative

of a function f(x) if the derivative of F(x) is f(X) or F

‘(x) = f(x)

• Examples :

1. F(x) = x

2

_{+ 3  f(x) = 2x}

2. F(x) = x

2

_{– 10  f(x) = 2x}

3. F(x) = x

2

_{+ 15  f(x) = 2x}

• If F ‘(x) = f(x) then the functions of the form F(x) + C

are antiderivative of f(x)

• The process for finding antiderivative is called

antidifferentiation

or

integration

.

• Notation :

The Indefinite Integral

Integration Formula





etc

....

....

C

x

sin

dx

x

cos

x

cos

x

sin

dx

d

.

3

2

1











 

...

r

x

dx

d

.

b

C

x

dx

x

dx

d

.

a

r

































1

1

1



















1

1

1

r

C

r

x

dx

x

r

r

Problems











dx

x

)

dx

x

)

dx

x

)

dx

x

sin

x

cos

)

dx

x

cos

x

sin

)

3

3 2

2

2

1

5

4

3

2

1

























dx

x

x

)

dx

x

x

)

dx

)

dx

x

cos

x

sin

)

dx

x

cos

x

tan

x

sec

)

3

2

3 2

3

10

2

9

8

2

7

6

The Properties of Indefinite Integral





cf

(

x

)

dx



c

f

(

x

)

dx

)

1





_

_



f

(

x

)



g

(

x

)

dx



f

(

x

)

dx



g

(

x

)

dx

)

2





















dx

x

x

x

sin

x

.

dx

x

x

.

dx

x

x

.

:

Examples

2

2

2

2

3

1

2

1

1

• Let y = (fog)(x). The derivative of y with respect

to x is y ‘ = (fog)’(x) = f ‘(g(x)) g’(x) [ The Chain

rule]

• If u = g(x) then the formula of integration is

Integration by Substitution

 

g

(

x

)

C

F

C

)

u

(

F

du

)

u

(

f

dx

dx

du

)

u

(

f

dx

'

u

)

u

(

f



















Problems

 





















dx

x

sin

x

cos

)

dx

x

cos

x

sin

)

dx

x

x

x

)

dx

x

x

cos

)

dx

x

x

)

2

2

2

2

2

5

4

1

2

1

3

1

2

1

2

1









 

 

















dx

x

sec

x

)

dx

x

sin

)

dx

x

x

)

dx

x

cos

x

sin

)

dx

x

)

x

3

2

2

2

1

3

2

3

5

10

9

1

8

2

5

2

7

2

1

6

• How to find the area of a region D bounded

below by the x-axis, on the sides by the lines x = a

and x = b , and above by a curve y = f(x), where

f(x) is continuous on [a,b] and f(x) ≥ 0 for all x in

(a,b)

• D = { (x,y) | a ≤ x ≤ b, 0 ≤ y ≤ f(x) }

1. Divide [a,b] into n subintervals by choosing points x1,

x2, …,xn such that a < x1 < x2 < …< xn < b. These

points are said to form a partition of [a,b]. Let



x1,



x2, …,



xn are the length of the partition.

2. Choose the any point x1,x2,…,xn in subinterval and

we have a

Riemann sum

:

f(x1)



x1 + f(x2)



x2 + … + f(xn)



xn =

3. Increase n ( n 



) in such a way the length of the

partition approaches zero (



xk  0 ) and form the

limit

Steps : The Definite Integral

 







n

k

xk

k

x

f

1

 

_

 





















n

k

n

n

k

xk

lim

0

₁

f

x

k

xk

lim

₁

f

x

k

xk

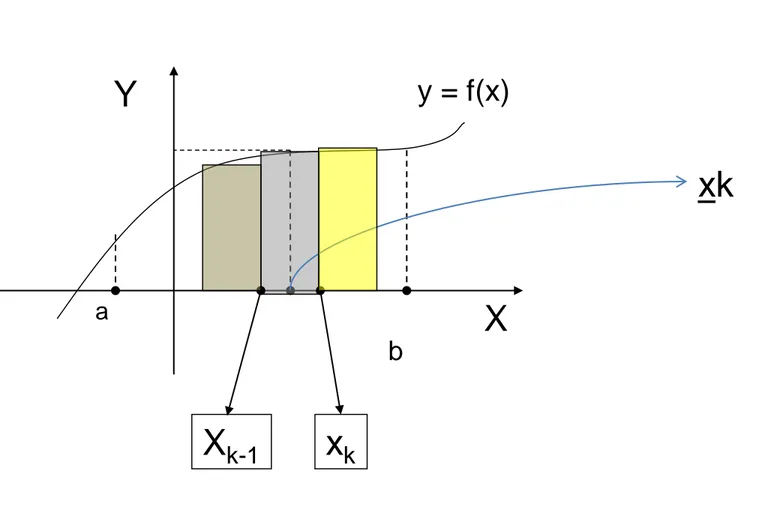
Illustration : The Definite Integral

y = f(x)

X

Y

b a

x

_k

X

_k-1

xk

• If a function f(x) is defined on [a,b], then the

Definite

Integral

of f(x) from a to b is defined to be (provided the

limit exits)

• If the limit exits then the function f(x) is said

integrable

on [a,b]

• The values a and b are called respectively

lower

and

upper limits of integration

and f(x) is called the

Integrand

.

Definition : The Definite Integral

 

_

 

























n

k

n

n

k

xk

b

a

xk

k

x

f

lim

xk

k

x

f

lim

dx

)

x

(

f

1

1

0

• If f(x) is continuous on [a,b] and F(x) is

antiderivative of f(x) on [a,b] then

The First Fundamental Theorem

)

a

(

F

)

b

(

F

a

b

)

x

(

F

dx

)

x

(

f

b

a













 2

0

2

1

2

1

dx

x

cos

)

(

dx

x

)

(

:

Examples

The Properties of Definite Integral









_







































) b ( g ) a ( g b a b c c a b a a b b a a a b a b a b a

du

)

u

(

f

dx

)

x

(

'

g

)

x

(

fog

)

(

dx

)

x

(

f

dx

)

x

(

f

dx

)

x

(

f

)

(

dx

)

x

(

f

dx

)

x

(

f

)

(

dx

)

x

(

f

)

(

dx

)

x

(

g

q

dx

)

x

(

f

p

dx

)

x

(

qg

)

x

(

f

p

)

(

5

4

3

0

2

1

Problems



































_

_

   2 0 2 4 1 9 4 3 1 2

3

2

5

2

4

5

3

3

2

2

1

1

2 6 2 3

dx

x

)

(

dt

t

t

sin

)

(

dx

x

x

x

)

(

dx

x

x

)

(

dx

x

)

(











 













  4 4 0 0 2 3 1 2 2 1 2 2 1

2

3

7

2

10

9

7

4

2

8

8

7

2

6

dt

t

sin

t

cos

)

(

dt

t

sec

t

tan

)

(

dx

x

x

x

)

(

dx

x

x

)

(

dx

x

)

(

• Let f(x) is continuous on open interval I and a



I.

If G(x) is defined by

Then G’(x) = f(x) at each point x in interval I

The Second Fundamental Theorem





x

a

dt

)

t

(

f

)

x

(

G

 

v

(

x

)

v

'

(

x

)

f

 

u

(

x

)

u

'

(

x

)

f

)

x

(

'

G

dt

)

t

(

f

)

x

(

G

)

x

(

v

)

x

(

u









_

Problems





)

x

(

"

F

and

)

x

(

'

F

dt

t

sin

)

x

(

F

)

(

g

sin

increa

only

is

)

x

(

F

which

erval

int

open

find

)

b

(

value

imum

min

its

attains

)

x

(

F

where

x

find

)

a

(

x

dt

t

t

)

x

(

F

)

(

)

(

"

H

and

)

(

'

H

dt

t

t

cos

)

x

(

H

)

(

)

(

"

G

and

)

(

'

G

dt

t

)

x

(

G

)

(

x x x x x









































3 2 2 0 2 0 2 2 2

4

7

3

3

0

0

3

2

2

2

1

3

1

• Let D is region that bounded below by the x-axis,

on the sides by the lines x = a and x = b , and

above by a curve y = f(x), where f(x) is continuous

on [a,b] and f(x) ≥ 0 for all x in (a,b) or D = { (x,y) |

a ≤ x ≤ b, 0 ≤ y ≤ f(x) }

• Then the area of D is

Area of Region (1)





b

a

dx

)

x

(

f

A

• Let D is region that bounded below by the x-axis,

on the sides by the lines x = a and x = b , and

above by a curve y = f(x), where f(x) is continuous

on [a,b] and f(x) ≤ 0 for all x in (a,b) or D = { (x,y) |

a ≤ x ≤ b, f(x) ≤ y ≤ 0 }

• Then the area of D is

Area of Region (2)







b

a

dx

)

x

(

f

A

• Find the area of region that bounded by the

curve y = sin x, x-axis, and on the sides by the

lines x = 0 and x = 3π/2

• Let D is region that bounded below by the line y

= c , on the sides by the y-axis and a curve x =

g(y), and above by the line y = d, where g(y) is

continuous on [c,d] and g(y) ≥ 0 for all y in (c,d) or

D = { (x,y) | 0 ≤ x ≤ g(y), c ≤ y ≤ d }

• Then the area of D is

Area of Region (3)





d

c

dy

)

y

(

g

A

• Let D is region that bounded below by the line y

= c , on the sides by the y-axis and a curve x =

g(y), and above by the line y = d, where g(y) is

continuous on [c,d] and g(y) ≤ 0 for all y in (c,d) or

D = { (x,y) | g(y) ≤ x ≤ 0, c ≤ y ≤ d }

• Then the area of D is

Area of Region (4)







d

c

dy

)

y

(

g

A

• Find the area of region that bounded by g(y) =

y

3

_{– 2y}

2

_{– 3y , y-axis and on the sides by the}

lines y = -1 and y = 4.

Example # 2

- 1/3 3 4

• Let D is region that bounded below by a curve y =

g(x), on the sides by the lines x = a and x = b , and

above by a curve y = f(x), where g(x) and f(x) are

continuous on [a,b] or D = { (x,y) | a ≤ x ≤ b, g(x) ≤

y ≤ f(x) }

• Then the area of D is

Area between two curves (1)











b

a

dx

)

x

(

g

)

x

(

f

A

• Let D is region that bounded below by the line y

= c , on the sides by a curve x = g(y) and a curve x

= f(y), and above by the line y = d, where g(y) and

f(y) are continuous on [c,d] and f(y) ≥ g(y) for all y

in (c,d) or D = { (x,y) | g(y) ≤ x ≤ f(y), c ≤ y ≤ d }

• Then the area of D is

Area between two curves (2)











d

c

dy

)

y

(

g

)

y

(

f

A

1. Find the area of the region enclosed by the

curves y = x

2

and y = 4x by integrating

a) With respect to x

b) With respect to y

2. Sketch the region enclosed by the curves and

find its area by any method

a) y = x

2

_{+ 4 and x + y = 6}

b) y = x

3

_{, y = - x and y = 8}

Sketch the region and find its area by any methods

1. y = x

3

_{– 4x, y = 0, x = 0, x = 2}

2. x = y

2

– 4y, x = 0, y = 0, y = 4

3. x

2

= y, x = y – 2

4. y

2

= - x, y = x – 6, y = - 1, y = 4

5. y = x

3

– 2x

2

, y = 2x

2

– 3x, x = 0, x = 3

Problems

Menghitung volume benda putar

Metoda Cakram



(

x

,

y

)

|

a

x

b

,

0

y

f

(

x

)



D











a. Daerah diputar terhadap sumbu x

a _b

f(x)

D

Benda putar

a _b f(x)

D

x



Untuk menghitung volume benda putar gunakan pendekatan Iris , hampiri, jumlahkan dan ambil limitnya.

Jika irisan berbentuk persegi panjang dengan tinggi f(x) dan alas diputar terhadap sumbu x akan diperoleh suatu cakram lingkaran dengan tebal dan jari-jari f(x).

x



x



x

x

f

V









2

(

)





b a

dx

x

f

V



2

(

)

sehingga

x



f(x)

Contoh: Tentukan volume benda putar yang terjadi jika daerah D yang dibatasi oleh , sumbu x, dan garis x=2 diputar terhadap sumbu x

2

x

y



2 x y  2 x  2

x

Jika irisan diputar terhadap sumbu x akan diperoleh cakram dengan jari-jari

dan tebal 2

x



x

Sehingga

x

x

x

x

V











2 2 4

)

(





Volume benda putar









2 0 2 0 5 4

5

32

|

5







x

dx

x

V

 2 x



(

x

,

y

)

|

c

y

d

,

0

x

g

(

y

)



D











b. Daerah

diputar terhadap sumbu y

c d

x=g(y) D

Daerah D Benda putar

c d

Untuk menghitung volume benda putar gunakan pendekatan Iris , hampiri, jumlahkan dan ambil limitnya.

c d x=g(y) D y 

Jika irisan berbentuk persegi panjang dengan tinggi g(y) dan alas diputar terhadap sumbu y akan diperoleh suatu cakram lingkaran dengan tebal dan Jari-jari g(y). y 

y



y  ) ( y g sehingga

y

y

g

V









2

(

)





d c

dy

y

g

V



2

(

)

Contoh : Tentukan volume benda putar yang terjadi jika daerah yang dibatasi oleh garis y = 4, dan sumbu y diputar terhadap sumbu y

2 x y 2 x y  4 y 

Jika irisan dengan tinggi dan tebal diputar terhadap sumbu y akan diperoleh cakram dengan jari-jari dan tebal

y y y y y y y  Sehingga

y

y

y

y

V













2



)

(

Volume benda putar









4 0 4 0 2

8

|

2







ydy

y

V

y x  

7.2.2 Metoda Cincin



(

x

,

y

)

|

a

x

b

,

g

(

x

)

y

h

(

x

)



D











a. Daerah

diputar terhadap sumbu x

h(x) g(x) a b D Daerah D Benda putar

h(x)

g(x)

a x b D

Untuk menghitung volume benda putar gunakan pendekatan Iris , hampiri, jumlahkan dan ambil limitnya.

Jika irisan berbentuk persegi panjang

dengan tinggi h(x)-g(x) dan alas diputar terhadap sumbu x akan diperoleh suatu

cincin dengan tebal dan jari –jari luar h(x) dan jari-jari dalam g(x).

x



x



x



sehingga

x

x

g

x

h

V











(

2

(

)

2

(

))







b a

dx

x

g

x

h

V



(

2

(

)

2

(

))

h(x) g(x)

Contoh: Tentukan volume benda putar yang terjadi jika daerah D yang dibatasi oleh , sumbu x, dan garis x=2 diputar terhadap garis y=-1

2 x y  2 x y  x  ₂ y=-1 1 2 1 x D

Jika irisan diputar terhadap garis y=1 Akan diperoleh suatu cincin dengan Jari-jari dalam 1 dan jari-jari luar 2

1 x Sehingga

x

x

V













((

2

1

)

2

1

2

)

x

x

x













(

4

2

2

1

1

)

x

x

x









(

4

2

2

)

















2 186₁₅ 3 16 5 32 2 0 3 3 2 5 5 1 2 4

)

(

)

|

(

2









x

x

dx

x

x

V



(

x

,

y

)

|

a

x

b

,

0

y

f

(

x

)



D











Metoda Kulit Tabung

Diketahui

f(x)

a b

D

Jika D diputar terhadap sumbu y diperoleh benda putar

Daerah D _{Benda putar}

Untuk menghitung volume benda putar gunakan pendekatan Iris , hampiri, jumlahkan dan ambil limitnya.

f(x) a b D x 

x



x 

Jika irisan berbentuk persegi panjang

dengan tinggi f(x) dan alas serta berjarak x dari sumbu y diputar terhadap sumbu y akan diperoleh suatu kulit tabung dengan tinggi f(x), jari-jari x, dan tebal

x f(x) x

x



sehingga

x

x

f

x

V







2



(

)





b a

dx

x

xf

V

2



(

)

Contoh: Tentukan volume benda putar yang terjadi jika daerah D yang dibatasi oleh , sumbu x, dan garis x=2 diputar terhadap sumbu y

2 x y  2 x y  x  ₂ 2 x D x

x



Jika irisan dengan tinggi ,tebal

dan berjarak x dari sumbu y diputar terhadap sumbu y akan diperoleh kulit tabung

dengan tinggi , tebal dan jari jari x 2

x

2

x



x

Sehingga

x

x

x

x

x

V











2 3

2

2





Volume benda putar









2 0 2 0 4 3

8

|

2

2



x

dx



x



V

Catatan :

-Metoda cakram/cincin

Irisan dibuat tegak lurus terhadap sumbu putar

- Metoda kulit tabung

Irisan dibuat sejajar dengan sumbu putar

Jika daerah dan sumbu putarnya sama maka perhitungan dengan menggunakan metoda cakram/cincin dan metoda kulit tabung akan menghasilkan hasil yang sama

Contoh Tentukan benda putar yang terjadi jika daerah D yang dibatasi Oleh parabola ,garis x = 2, dan sumbu x diputar terhadap

a. Garis y = 4 b. Garis x = 3

2 x y 

a. Sumbu putar y = 4 (i) Metoda cincin

2 x y  2 D y=4 x 

Jika irisan diputar terhadap garis y=4 akan diperoleh cincin dengan

Jari-jari dalam = r_d  (4 x2) ) 4 (  x2 Jari-jari luar = 4

r

_l



4

Sehingga

x

x

V













((

4

)

2

(

4

2

)

2

)

x

x

x









(

8

2 4

)

Volume benda putar

















2 224₁₅ 5 32 3 64 2 0 5 5 1 3 3 8 4 2

)

(

|

)

(

)

8

(









x

x

dx

x

x

V

(ii) Metoda kulit tabung 2 x y  2 D y=4 y  y

Jika irisan diputar terhadap garis y=4 akan diperoleh kulit tabung dengan

Jari-jari = r = y  4 y  4 y  2 Tinggi = h = 2 y Tebal =



y

Sehingga

y

y

y

V











2



(

4

)(

2

)

y

y

y

y

y











2



(

8

4

2

)

Volume benda putar



    4 0 ) 2 4 8 ( 2 y y y y dy V



4 0 2 / 5 5 2 2 2 / 3 3 8

₎

_|

8

(

2

y



y



y



y







224₁₅



b. Sumbu putar x=3 (i) Metoda cincin

2 x y  2 D y 

x=3 Jika irisan diputar terhadap garis x=3 diperoleh cincin dengan

Jari-jari dalam = 1 1  d r Jari-jari luar = 3 y ₃ _y y r_l 3 Sehingga

y

y

V













((

3

)

2

(

1

)

2

)

y

y

y











(

8

6

)

Volume benda putar

dy

y

y

V









4 0

)

6

8

(







(

8

y



4

y

3/2



8

|

₀4

)



8



(ii) Metoda kulit tabung 2 x y  2 D x  x=3 x

Jika irisan diputar terhadap garis x=3 diperoleh kulit tabung dengan

Tinggi = h = 2

x

2 x Jari-jari = r = 3 3-x 3-x Tebal =



x

Sehingga

x

x

x

V









2

)

3

(

2



x

x

x







2



(

3

2 3

)

Volume benda putar







2 0 3 2

)

3

(

2

x

x

dx

V





2



(

_x

3



1₄

_x

4

)

|

₀2



2



(

8



4

)



8



Hitung volume benda putar dari daerah yang

terletak di kuadran pertama yang dibatasi oleh y

2

=

x

3

_{, garis y = 8 dan sumbu Y, bila diputar}

mengelilingi

1. Sumbu Y

2. Sumbu X

3. Garis x = 4

4. Garis y = 8

Soal Latihan