G E O M E T R I
Untuk Memenuhi Tugas Mata Kuliah Filsafat Ilmu Dosen Pengampu : Dr. Gatut Iswahyudi, M.Si.
Oleh,
1. Berti Okta Sari (S851402006) 2. Yudi Pramono Pawiro (S851402070)
PROGRAM MAGISTER PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SEBELAS MARET SURAKARTA
A. Pendahuluan
Geometri adalah sebagian dari matematik yang mengambil persoalan menenai saiz, bentuk, dan kedudukan relatif dari sifat ruang. Pada mulanya ia hanya sebagian dari pengetahuan praktis yang menitik beratkan pada jarak luas dan isi, tetapi pada abad ke 3SM geometri telah diletakkan di dalam bentuk aksioma oleh euclid membentuk geometri euclid. Sedangkan Geometri berasal dari bahasa Yunani (greek) yang berarti ukuran bumi. Maksudnya mencakup mengukur segala sesuatu yang ada di bumi. Geometri kuno sebagian dimulai dari pengukuran praktis yang diperlukan untuk pertanian orang–orang Babylonia dan Mesir. Kata “geometri” menurut orang Mesir dan Babyloni ini diperluas untuk perhitungan panjang ruas garis, luas dan volume.
Geometri euclid adalah pembelajaran geometri yang di dasarkan pada definisi, teorem atau aksioma (titik,garis dan bidang) dan asumsi-asumsi dari seseorang matematikawan Yunani (330 B.C.) yakni Euclid. Banyak penemuan-penemuan Euclid telah di dahului oleh matematikawan yunani, tetapi penemuan-penemuan itu tidak tersruktur dengan rapi seperti yang dilakukan euclid. Euclid membuat pola deduktif secara komprehensip untuk membentuk geometri. Pendekatan dari euclid terdiri dari pembuktian semua teorema dan aksioma-aksiomanya.
Dalam pembelajaran matematika di sekolah, geometri lebih berkenaan dengan bangun-bangun geometri, garis dan sudut, kesebangunan, kekongruenan, transformasi, dan geometri analitis. Geometri merupakan bagian dari matematika yang mempelajari pola-pola visual, yang akan menghubungkan matematika dengan dunia nyata. Geometri juga dapat dipandang sebagai sistem matematika yang menyajikan fenomena yang bersifat abstrak (tidak nyata), akan tetapi dalam pembelajarannya bertahap didahului dengan benda-benda kongkret sebagai media sesuai dengan tahap perkembangan anak.
Tidak ada yang bisa menetapkan seberapa besar garis atau sisi sebuah persegipanjang. Hal-hal tersebut tak pernah terungkap disaat membicarakan persegipanjang dan juga benda-benda geometri yang lainnya. Akan tetapi mereka ada dan dapat dipelajari sebagai materi matematika yang sangat bermanfaat dalam kehidupan sehari-hari dan juga dalam pengembangan ilmu dan teknologi.
Kalaupun obyek geometri itu abstrak, akan tetapi mereka “ada”. Hal tersebut merupakan kenyataan bahwa geometri sebagai suatu aspek matematika yang sangat penting dan berperan dalam kehidupan. Geometri menjadi materi yang ingin diketahui secara mendasar dan fundamental untuk pengembangan matematika itu sendiri dan pengembangan kemampuan berpikir manusia secara logis. Oleh karena itu perlu adanya tinjauan tentang ”geometri” tersebut berdasarkan filasafat matematika.
B. Pembahasan 1. Euclid
Pendapat Holes telah ada dalam argumen Euclid selama seratus tahun terakhir. Hilbert menemukan sejumlah asumsi yang belum dipecahkan Euclid dalam melakukan formulasi penuh dari secara explicit diperlukan untuk pengembangan ketat geometri Euclidean sekarang tersedia. Presentasi Euclid jauh lebih rumit dan jauh lebih sedikit dibaca, dan kita harus bertanya apa sebenarnya titik axiomatization. Euclid memerlukan asumsi untuk membuktikan teorema secara geometri, tapi butuh asumsi lain keteraturan dan kontinuitas untuk diberikan. Jika kita ingin menemukan sejumlah asumsi seperti yang telah dilakukan Hilbert maka kita harus membuat semua asumsi secara eksplisit.
logika formal, pendekatan aksiomatik masih jauh lebih dipahami dalam bahasa Euclid daripada Hilbert.
Fisikawan sering menyajikan mekanika Newton, teori relativitas, teori relativitas umum dan mekanika kuantum dalam hal aksioma, apa asumsi cahaya tinggi khas dari teori tersebut, namun mengambil banyak untuk diberikan. Ini adalah prosedur yang sangat masuk akal, tidak hanya untuk menyajikan masalah untuk siswa, tetapi untuk mengidentifikasi kerja secara profesional. Untuk mengidentifikasi sebagian besar atau sebagian saja dari geometri Euclidean yang menjadi kebutuhan kita adalah untuk membedakan karakteristik unik dari geometri lain yang cukup mungkin disajikan di tempat. Setiap baris mendefinisikan perintah terus menerus dan tidak biasanya dalam pertanyaan, dan hanya mengacaukan komunikasi antisipasi pertanyaan yang tidak akan bertanya. Singkatnya tidak hanya jiwa kecerdasan, namun kondisi komunikasi. Jumlah eksplisit sering tidak hanya tidak beralasan. Euclid tidak boleh disalahkan karena kurangnya ketelitian, tetapi dipuji karena rasa yang relevan.
2. Lima Aksioma
a. Unsur yang Tidak Didefinisikan (Undefined Term), Definisi dan Postulat
Sebagai struktur matematika, geometri membicarakan unsur-unsur yang tidak didefinisikan dan relasi antara unsur tersebut. Dalam hal ini unsur-unsur yang tidak didefinisikan adalah titik, garis, bidang, dan ruang serta relasi yang tidak didefinisikan yaitu terletak pada dan keantaraan. Selanjutnya unsur-unsur yang tidak didefinisikan tersebut memerlukan simbol-simbol agar dalam pembahasan berikutnya lebih mudah dipahami.
1) Titik dan Garis
Titik dituliskan dengan huruf kapital tunggal, seperti …
Garis dituliskan dengan huruf kecil, seperti … atau dengan dengan menggunakan dua titik pada garis. Misal garis (dituliskan )
Bidang disimbolkan dengan huruf kecil atau huruf-huruf Yunani seperti α (alpa), β (beta), γ (gamma) yang diletakkan di daerah dalam bidang tersebut.
Unsur-unsur yang tidak didefinisikan tersebut kemudian dikembangkan menjadi unsur-unsur yang didefinisikan, aksioma atau postulat, dan teorema seperti ruas (segment) garis, sinar garis, dan sudut. Euclid sebagai salah satu murid dari akademi Plato di Athena memperbarui teorema Plato yang belum sempurna bersama dengan Eudoxus dan menghasilkan lima aksioma atau postulat khusus yang dalam bahasa Yunani (aitemata) yang artinya (koinai ennoiai), misalnya jika a sama dengan b, dan b sama dengan c, maka a sama dengan c. Geometri Euclid merupakan satu sistem aksioma, yang mana semua teorema ("penyataan benar") adalah diambil daripada satu bilangan aksioma-aksioma yang terhingga. Geometri Euklides merupakan sistem aksiomatik, di mana semua teorema ("pernyataan yang benar") diturunkan dari bilangan aksioma yang terbatas.Berdasarkan pada geometri Euclid ada lima asumsi dasar yang disebut aksioma atau postulat.
a) Postulat I Euclid 2.1 (Marvin Jay Greenberg, 1974: 12)
Pada postulat I Euclid sering pula dinyatakan dengan, dua titik menentukan sebuah garis tunggal. Untuk menyatakan postulat Euclid yang kedua sebelumnya akan didefinisikan terlebih dahulu definisi ruas (segment) garis.
Definisi 2.1 (Sri Mulyati: 20)
Ruas (segment) garis AB adalah himpunan titik yang memuat titik A dan titik B serta semua titik yang terdapat diantara titik A dan titik B tersebut.
Gambar 2.2 Ruas garis AB
Pada ruas garis AB, titik A dan B masing-masing disebut ujung (titik akhir) dari ruas garis AB, dan dapat disimbolkan .
digunakan kata “kongruen” daripada kata “sama” untuk menjelaskan istilah-istilah yang digunakan dalam pembahasan selanjutnya, karena akan lebih mudah dipahami. Sedangkan, objek atau benda yang mempunyai bentuk dan ukuran yang sama disebut kongruen. Kongruen dapat dikenakan pada dua ruas garis, dua sudut, dan dua segitiga atau objek lainnya, dan penjelasan mengenai istilah-istilah tersebut akan dijelaskan pada pembahasan sub bab selanjutnya.
b) Postulat II Euclid 2.2 (Marvin Jay Greenberg, 1974: 12)
Untuk setiap dan untuk setiap terdapat titik tunggal sedemikian sehingga diantara dan serta kongruen dengan. Namun oleh Moeharti Hw (1986) menyebutkan postulat kedua Euclid bahwa memperpanjang suatu ruas garis secara terus memerus atau kontinu untuk menjadi suatu garis lurus.
Definisi 2.2 (Marvin Jay Greenberg,1974: 13)
Diberikan dua titik dan himpunan semua titik P sedemikian sehingga kongruen dengan disebut lingkaran dengan disebut pusat lingkaran dan disebut jari-jari (radius) lingkaran.
Dari definisi 2.2 tersebut selanjutnya akan menyatakan postulat ketiga Euclid. c) Postulat III Euclid 2.3 (Marvin Jay Greenberg,1974: 13)
Untuk setiap titik dan setiap titik yang tidak sama dengan terdapat lingkaran dengan pusat dan jari-jari (radius) .
Definisi 2.3 (Barnett Rich, 1977:2)
Sinar garis adalah bagian dari garis lurus yang dimulai dari sebuah titik tertentu dan diperpanjang secara tak terbatas ke suatu arah.
Gambar 2.3 Sinar garis AB
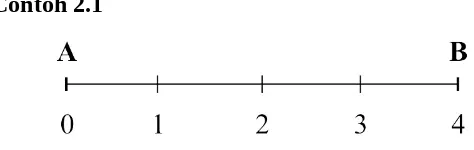
Untuk ukuran dapat dinyatakan dengan . Sebagai contoh pada gambar 2.4 ukuran adalah 4 atau dituliskan = 4.
Contoh 2.1
Gambar 2.4 Ruas garis AB dan ukurannya
Berdasarkan ukuran ruas garis tersebut dapat didefinisikan apa yang dimaksud dengan titik tengah suatu ruas garis.
Definisi 2.4 (Sri Mulyati: 22)
Titik tengah suatu ruas garis adalah titik pada ruas garis sehingga membentuk dua ruas garis yang berukuran sama.
Gambar 2.5 Ruas garis AB dengan titik tengah M
Pada gambar 2.5 titik M adalah titik tengah dari . Setiap segmen memiliki tepat satu titik tengah sehingga karena M titik tengah dari . Garis yang memotong ruas garis di titik tengah disebut bisektor ruas garis atau garis bagi ruas garis.
Contoh 2.2 :
Gambar 2.6 Bisektor ruas garis AB
i) Sudut dan Ukuran Sudut
Definisi 2.5 (Sri Mulyati: 22)
Sudut adalah himpunan titik-titik yang merupakan gabungan dari dua sinar yang titik pangkalnya sama (satu titik pangkal).
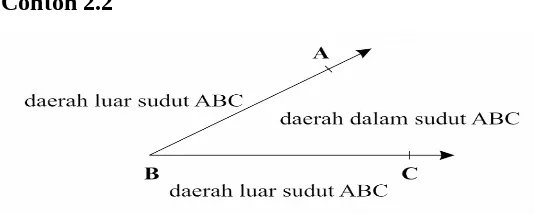
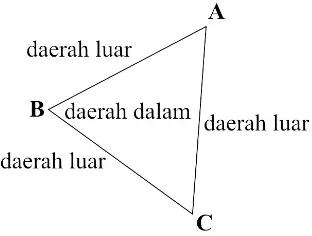
Gambar 2.7 berikut ini menggambarkan sudut ABC dan ditulis , disebut kaki-kaki sedangkan titik B disebut titik sudut dan diatas juga dapat ditulis sebagai . Selanjutnya membagi bidang yang memuatnya menjadi tiga himpunan yang saling lepas yaitu sudut itu sendiri yaitu , daerah dalam (interior) , dan daerah luar (eksterior) , seperti yang ditunjukkan pada gambar 2.7.
Contoh 2.2
Gambar 2.7 Daerah dalam dan daerah luar sudut ABC ii) Postulat Ukuran Sudut 2.4 (Kusno, 2004:63)
a. Ukuran sudut merupakan fungsi dari himpunan sudut ke himpunan bilangan real R
b. Untuk setiap maka ukuran (ditulis m) terletak antara sampai 180 c. Untuk setiap atau dan untuk setiap bilangan r diantara dan 180
pada sisi yang sepihak dengan atau ada tepat satu sehingga diperoleh
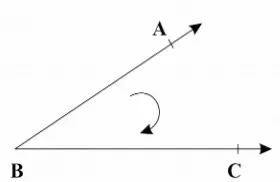
Gambar 2.8 Sudut dengan menunjukkan arah putaran Definisi 2.6 (Sri Mulyati: 24)
Sudut yang berukuran kurang dari 90 disebut sudut lancip, sedangkan sudut yang ukuran sudutnya sama dengan 90 disebut dengan sudut siku-siku dan sudut yang berukuran lebih besar dari 90 disebut sudut tumpul.
Menurut definisi, untuk membentuk sudut maka diperlukan dua sinar garis yang titik pangkalnya berhimpit. Sudut yang berukuran 0 artinya untuk menghimpitkan kaki sudut yang satu dengan kaki sudut yang lain dan tidak memerlukan adanya pemutaran. Dengan demikian kedua kaki sudut telah berhimpit atau dengan kata lain hanya ada satu sinar garis. Oleh karena itu, sebuah sinar garis dianggap sebagai sudut yang berukuran 0. Sedangkan sudut yang berukuran 180, kedua kaki sudut membentuk sebuah garis. Sehingga, sebuah garis juga dapat dianggap sebagai sudut yang berukuran 180 atau sering pula disebut sebagai sudut lurus.
Definisi 2.7 (Sri Mulyati: 24 )
Dua sudut dikatakan berpelurus (suplementary), jika jumlah ukuran sudutnya adalah 180, sedangkan dua sudut dikatakan berpenyiku (complementary), jika jumlah ukuran sudutnya adalah 90. Selanjutnya dapat menyatakan postulat keempat Euclid yang menyatakan mengenai sudut.
d) Postulat IV Euclid 2.5 (Marvin Jay Greenberg, 1974: 16)
Semua sudut siku-siku adalah kongruen dengan sudut siku-siku yang lain. Definisi 2.8 (Kusno, 2004: 63)
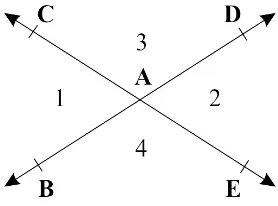
Pada gambar 2.9 berikut dan adalah dua sinar yang berlawanan dan terletak pada satu garis yaitu , namun kedua sinar tersebut memiliki titik pangkal yang sama yaitu titik C.
Gambar 2.9 dan adalah dua sinar yang berlawanan Definisi 2.9 (Sri Mulyati: 35)
Sudut-sudut bertolak belakang adalah dua buah sudut yang sedemikian rupa sehingga kaki-kaki sudut yang satu merupakan sinar-sinar yang berlawanan dengan kaki-kaki sudut yang lain.
Gambar 2.10 Sudut-sudut yang bertolak belakang
Berdasarkan gambar 2.10 tampak bahwa sudut-sudut yang saling bertolak belakang adalah kongruen dan dapat dibuktikan sebagai berikut:
Diberikan sudut bertolak belakang dan , dan adalah dua sinar yang arahnya berlawanan, begitu juga dengan dan , dan membentuk garis lurus, begitu juga dengan dan . Di lain pihak, merupakan pelurus untuk dan juga pelurus untuk maka jelas keduanya kongruen.
a. Segiempat
Pada sub bab ini akan menjelaskan mengenai segiempat yang meliputi jajar genjang, persegi panjang, belah ketupat, persegi dan trapesium. Definisi 2.10
Gambar 2.11 Segiempat ABCD
Segiempat terdiri dari empat ruas garis yang disebut sisi. Setiap ujung sisi yang satu berhimpit dengan dengan titik sudut yang lain dan tidak ada dua sisi yang terletak segaris, serta tidak ada dua sisi yang saliang berpotongan selain di titik ujung. Pasangan dua sisi yang tidak memiliki titik persekutuan disebut pasangan sisi yang berhadapan. Pada Gambar 2.11, merupakan pasangan sisi yang berhadapan adalah dengan dan dengan . Pasangan dua sisi yang memiliki titik persekutuan disebut pasangan sisi yang berdekatan yaitu dengan , dengan , dengan , dan dengan . Sedangkan dengan disebut diagonal.
Pada segiempat ABCD terbentuk empat buah sudut. Pasangan sudut yang tidak memiliki kaki persekutuan disebut pasangan sudut yang berhadapan yaitu dengan dan dengan . Pasangan sudut yang memiliki kaki persekutuan disebut pasangan sudut yang bersisian yaitu dengan , dengan , dengan , dan dengan .
1. Jajar Genjang
Definisi 2.11 (Kusni, 2004:2)
Jajar genjang ialah suatu segiempat yang memiliki sisi-sisi yang berpasangan sejajar.
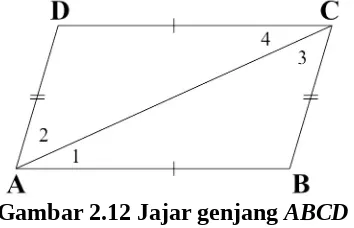
Gambar 2.12 Jajar genjang ABCD
Pasangan sisi yang berdekatan yaitu dengan , dengan , dengan , dan dengan . Pasangan sisi yang berhadapan adalah dengan dan dengan .
Teorema 2.1 (Kusni, 2004:2)
Diketahui : ABCD Jajar genjang Buktikan : dan
Bukti:
Dibuat diagonal .
(Sudut dalam berseberangan) (Sudut dalam berseberangan) Maka,
Sehingga
Dengan membuat diagonal dan dengan cara yang sama didapat . Teorema 2.2 (Kusni, 2004:3)
Sisi-sisi jajar genjang yang berhadapan sama panjang. Diketahui : ABCD jajar genjang.
Akan dibuktikan: dan . Bukti:
Lihat gambar 2.12
(Sudut dalam berseberangan) (Sudut dalam berseberangan)
Sehingga memenuhi (Sd.S.Sd) Akibatnya dan .
Teorema 2.3 (Kusni, 2004:4)
Jika dalam suatu segiempat, sudut-sudut yang berhadapan sepasang-sepasang sama besar maka segiempat itu suatu jajar genjang.
Diketahui : ABCD segiempat dan
Akan dibuktikan : ABCD jajar genjang Bukti :
Karena maka .
Jika dalam suatu segiempat, sudut-sudut yang berhadapan sepasang-sepasang
Karena maka .
Berhubung dan maka segiempat ABCD adalah jajar genjang. Sifat-sifat jajar genjang yang lain yaitu:
a. Kedua diagonal jajar genjang memotong di titik tengah.
b. Jika dalam suatu segiempat sisi-sisi yang berhadapan sepasang-sepasang sama panjang maka segiempat itu suatu jajar genjang.
c. Jika dalam suatu segiempat diagonal-diagonal memotong di tengah maka segiempat itu suatu jajar genjang.
d. Jika dalam suatu segiempat dua sisi sama dan sejajar maka segiempat itu suatu jajar genjang
2. Persegi panjang
Definisi 2.12 (Kusni, 2004:5)
Persegi panjang ialah suatu jajar genjang yang satu sudutnya siku-siku.
Gambar 2.13 Persegi panjang ABCD Akibatnya :
a. Jajar genjang ke empat sudutnya siku-siku.
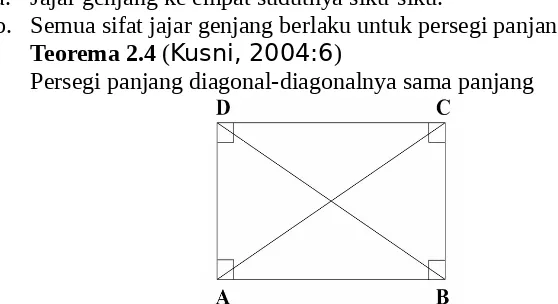
b. Semua sifat jajar genjang berlaku untuk persegi panjang. Teorema 2.4 (Kusni, 2004:6)
Persegi panjang diagonal-diagonalnya sama panjang
Gambar 2.14 Persegi panjang ABCD dengan diagonal dan Diketahui : ABCD persegi panjang
Akan dibuktikan : Bukti :
Lihat dan
(berimpit) (diketahui)
Maka (S Sd S), akibatnya .
3. Belah ketupat
Definisi 2.13 (Kusni, 2004:6)
Belah ketupat ialah jajar genjang yang dua sisinya yang berurutan sama panjang.
Gambar 2.15 Belah ketupat ABCD Akibatnya:
a. Belah ketupat keempat sisinya sama panjang.
b. Sifat-sifat pada jajar genjang berlaku untuk belah ketupat.
c. belah ketupat diagonal-diagonalnya membagi sudut-sudut sama besar dan diagonal-diagonal saling tegak lurus sesamanya
d. Jika dalam jajar genjang suatu diagonal membagi dua suatu sudut sama besar maka jajar genjang itu suatu belah ketupat.
e. Jika dalam suatu jajar genjang diagonal-diagonalnya tegak lurus sesamanya maka jajar genjang itu suatu belah ketupat.
4. Persegi
Definisi 2.14 (Kusni, 2004:8)
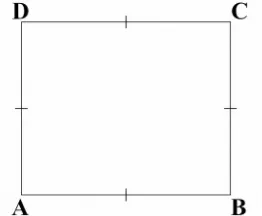
Persegi ialah suatu segiempat yang semua sisinya sama panjang dan satu sudutnya siku-siku
Akibatnya persegi, keempat sudutnya siku-siku. Persegi juga disebut segiempat beraturan. Pada persegi berlaku sifat-sifat belah ketupat maupun persegi panjang.
b. Kekongruenan
Selanjutnya pada pembahasan ini akan dibahas mengenai kekongruenan ruas garis, sudut dan segitiga serta untuk menyatakan kongruensi digunakan simbol ” “.
1. Kekongruenan ruas garis dan sudut Definisi 2.15
a. dikatakan kongruen dengan (ditulis ) jika dan hanya jika . b. dikatakan kongruen dengan (ditulis ) jika dan hanya jika .
Kongruensi di antara ruas garis dan di antara sudut merupakan relasi ekuivalen, yaitu relasi yang memenuhi tiga sifat. Tiga sifat tersebut adalah a. Refleksi
Pada kongruensi ruas garis dan kongruensi pada sudut . b. Simetri
Pada kongruensi ruas garis jika maka , dan kongruensi pada sudut jika maka
c. Transitif
Pada kongruensi ruas garis jika dan maka , dan kongruensi pada sudut dan maka .
2. Kekongruenan Segitiga
Sebelumya akan dijelaskan terlebih dahulu mengenai segitiga. Definisi 2.16 (Kusno, 2004)
Segitiga adalah gabungan tiga ruas garis yang dibentuk oleh tiga titik yang tidak segaris yang sepasang-sepasang saling dihubungkan. Ketiga ruas garis tersebut disebut sisi-sisi segitiga. Sudut-sudut yang terbentuk oleh pasangan-pasangan sisi-sisi tersebut disebut sudut-sudut segitiga, dengan titik-titik sudut ketiga titik tersebut.
Gambar 2.17 Daerah dalam dan daerah luar segitiga ABC
Seperti halnya pada sudut, segitiga juga memiliki daerah dalam (interior) dan daerah luar (eksterior) segitiga (lihat gambar 2.17).
Selanjutnya akan menjelaskan mengenai kekongruenan dua segitiga.
Gambar 2.18
Untuk menyatakan kongruensi segitiga pertama dengan segitiga kedua adalah dengan menggunakan korespondensi satu-satu antara titik-titik sudut segitiga pertama dengan titik-titik sudut segitiga kedua. Demikian pula untuk sisi-sisi segitiga dan sudut-sudut segitiga pertama berkoresponden dengan segitiga kedua. Untuk simbol korespondensi dalam sub bab ini menggunakan “”., , , dan , ,
Definisi 2.17 (Kusno, 2004)
Jika dan hanya jika terdapat korespondensi satu-satu antara dengan dan tiap pasangan sisi-sisi serta sudut-sudut yang berkorespondensi kongruen.
Dapat juga ditulis sebagai berikut: jika dan , , , , , .
Postulat 2.6 (S.Sd.S) (Sri Mulyati: 39)
segitiga pertama kongruen dengan bagian-bagian korespondingnya pada segitiga kedua.
Postulat 2.7 (Sd.S.Sd) (Sri Mulyati: 39)
Dua segitiga dikatakan kongruen jika terdapat koresponden satu-satu antara titik-titik sudutnya sehingga dua sudut dan sisi yang memuat sudut itu pada segitiga pertama kongruen dengan bagian-bagian korespondingnya pada segitiga kedua.
d. Postulat Kelima Euclid
Pada sub Bab ini akan menjelaskan mengenai postulat kelima Euclid. Berbeda dengan empat postulat Euclid sebelumya, postulat kelima Euclid telah menjadi kontroversi selama 19 abad. Postulat kelima Euclid disebut juga dengan postulat kesejajaran Euclid atau postulat paralel Euclid. Sebelum menjelaskan mengenai postulat kesejajaran Euclid akan didefinisikan terlebih dahulu mengenai garis sejajar (parallel).
Definisi 2.18 (Marvin Jay Greenberg,1974: 16)
Dua garis yaitu l dan m adalah sejajar (parallel) jika kedua garis tersebut tidak berpotongan , dengan kata lain jika tidak ada titik yang berada pada kedua garis tersebut. Dapat dituliskan .
Sebagai catatan, mengasumsikan bahwa garis-garis terletak pada satu bidang yang sama yaitu sesuai dengan kekentuan yang telah disepakati untuk titik dan garis terlatak pada satu bidang yang sama kecuali untuk menyatakan hal yang lain (Marvin Jay Greenberg, 1974). Selain itu, tidak perlu memikirkan bahwa jarak antara kedua garis yang sejajar (parallel) adalah sama namun dalam pembahasan ini hanya perlu diketahui bahwa dua garis sejajar (parallel) tidak pernah berpotongan.
Jika suatu garis lurus memotong dua garis lurus sedemikian sehingga jumlah sudut-sudut dalam sepihak jumlahnya kurang dari jumlah dua sudut siku-siku, maka kedua garis tersebut akan berpotongan dipihak tempat kedua sudut dalam sepihak yang jumlahnya kurang dari dua sudut siku-siku.
Postulat kelima Eucild yang selanjutnya disebut dengan postulat kesejajaran Euclid, berbeda dengan keempat postulat Euclid sebelumnya karena aksioma atau postulat dari geometri adalah sebagai abstraksi dari pengalaman atau percobaan. Dapat dilihat perbedaan dari keempat postulat Euclid dengan postulat kesejajaran Euclid, untuk dua postulat pertama adalah abstraksi dari hasil menggambar dengan garis lurus. Untuk postulat ketiga Euclid merupakan abstraksi dari hasil menggambar dengan jangka. Postulat keempat Euclid mungkin kurang jelas sebagai abstraksi namun postulat tersebut merupakan hasil mengukur sudut dengan busur derajat (dimana jumlah dari sudut berpelurus (supplementary) adalah 180, sehingga jika sudut berpelurus kongruen dengan yang lain, masing-masing berukuran 90).
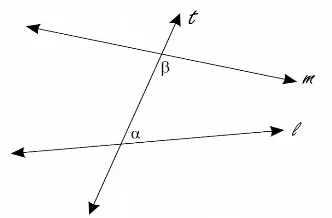
Gambar 2.19 Garis l dan m dipotong transversal t
Namun masalah kriteria ini tidak akan digunakan untuk meyakini kebenaran dari postulat kesejajaran Euclid karena ternyata secara logika ekivalen dengan proposisi 17 (Euclid’s Element Book I) yang menyebutkan bahwa dalam segitiga jumlah dari dua sudut dalam segitiga tersebut kurang dari dua sudut siku-siku, sehingga hanya akan menjadi alasan yang berputar atau melingkar.
Selanjutnya dengan adanya permasalahan bahwa postulat kesejajaran Euclid sukar untuk diuji secara jelas maka dalam bab selanjutnya akan dibahas mengenai ekuivalen dan upaya-upaya untuk membuktikannya. Menurut Walter Prenowitz dan Meyer Jordan (1965) sebelumnya mensketsa terlebih dahulu mengenai teori geometri bidang Euclid.
Dimulai dengan mendaftar sejumlah aksioma-aksioma untuk geometri bidang Euclid:
1. Sesuatu yang sama akan sama satu sama yang lainnya
2. Jika sesuatu yang sama ditambah dengan suatu yang sama, maka jumlahnya sama
3. Jika sesuatu yang sama dikurangi dengan sesuatu yang sama, sisanya sama 4. Benda-benda yang berhimpit satu sama lain, satu sama lain sama
5. Seluruhnya lebih besar dari sebagian
Selain itu ada beberapa postulat pada bidang Euclid, yaitu :
1. Bangun geometri dapat dipindahkan tanpa mengubah ukuran dan bentuknya
2. Setiap sudut memiliki bisector (garis bagi) 3. Setiap segmen memiliki titik tengah
1. Sudut bertolak belakang sama besar atau jika dua sudut bertolak belakang maka mereka kongruen. Maksud dari teorema ini telah dijelaskan pada definisi 2.10 pada penjelasan sub bab sebelumnya.
2. Sifat kongruensi segitiga (S.Sd.S, Sd.S.Sd, S.S.S)
a. Dua segitiga kongruen jika dua sisi yang bersesuaian sama panjang serta sudut yang diapitnya sama besar (S.Sd.S)
b. Dua segitiga kongruen jika dua sudut yang bersesuaian sama besar dan sisi yang diapitnya sama panjang (Sd.S.Sd)
c. Dua segitiga kongruen jika sisi-sisi yang bersesuaian sama panjang (S.S.S)
Gambar 2.20 dan
3. Teorema kesamaan sudut alas segitiga sama kaki
Jika dua sudut suatu segitiga kongruen maka sisi-sisi dihadapan sudut-sudut itu kongruen
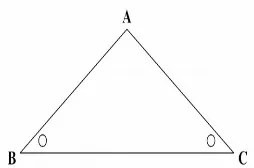
Gambar 2.21 Segitiga Sama kaki ABC Bukti:
Diketahui dan Dibuktikan
Telah diketahui maka menurut sifat simetri relasi maka … (*) Pandang dan , karena
(diketahui)
(sifat refleksi relasi ) (*)
Menurut aksioma atau postulat Sd.S.Sd maka , akibatnya . Terbukti. 4. Ekstensi garis yang tegak lurus pada garis pada titik garis tersebut
lurus g dan garis itu hanya satu-satunya. Sehingga untuk membuktikan perlu dibuktikan dulu ada garis yang tegak lurus dengan g, kemudian dibuktikan garis tersebut tunggal.
Gambar 2.22 (A) titik P pada garis g (B) garis g dipotong garis k
Jadi diketahui garis g dan titik P pada garis g, akan dibuktikan: 1) Di P ada garis yang tegak lurus g
2) Garis yang tegak lurus g tunggal
Bukti:
(i) Karena garis adalah himpunan titik maka ada titk A pada garis g dengan . Kemudian terdapat dan titik P pada sedemikan sehingga . Pada titik A terdapat (sudut lancip), demikian pula di B terdapat . Kemudian dan berpotongan di C, karena misalkan dan tidak berpotongan maka . maka . Diketahui , berarti , sehingga siku-siku. Maka kontradiksi, karena lancip. Jadi dan berpotongan di C. (Gambar 2.17 (B))
Dari C dan P terdapat . Pandang , karena , menurut convers teorema segitiga samakaki . Sehingga menurut teorema . Terbukti.■
(ii) Akan dibuktikan tunggal Menurut (i) ada garis di A dan maka
Misalkan ada garis lain yang melalui titik P yaitu , menurut teorema . Berarti di P terdapat lebih dari satu garis yang masing-masing sejajar garis k, yaitu dan . Padahal menurut postulat kesejajaran terdapat satu dan hanya satu garis yang sejajar suatu garis. Jadi pengandaian bahwa di P terdapat garis lain selain salah, namun tidak ada garis lain selain yang tegak lurus dengan g. Terbukti.
Di suatu titik P tidak pada garis g terdapat satu dan hanya satu garis yang tegak lurus.
Gambar 2.23 (A) titik P diluar garis g (B) titik Q pada garis g
Diketahui: garis g dan titik P tidak pada garis g. Gambar 2.17 (A)
Akan dibuktikan: melalui P terdapat satu dan hanya satu garis yang tegak lurus g
Bukti:
(i) Dibuktikan melalui P ada garis yang tegak lurus g
Titk A sembarang titik di garis g lalu dibuat . Di titik A pada garis g terdapat .
Sehingga dapat diperpanjang sehingga . Selanjutnya garis melalui P dan B dan memotong garis g di C. Pandang dan , karena , dan maka dan (S.Sd.S).
Akibatnya . Karena kedua sudut saling besisian maka menurut teorema (ii) Akan dibuktikan bahwa adalah satu-satunya garis yang tegak lurus
dengan garis g.
Misalkan ada garis lain yaitu dengan .
dan maka menurut teorema : . Menurut definisi garis sejajar berarti m dan tidak mempunyai titik sekutu kontradiksi karena garis m dan keduanya melalui titik P. Sehingga pengandaian bahwa ada garis lain yang melalui titik P tegak lurus garis g adalah salah, sehingga yang benar tidak ada garis lain yang melalui titik P yang tegak lurus garis g selain Jadi adalah satu-satunya garis yang melalui
Sekarang akan dibuktikan teorema sudut luar, sebagai cara menuju perkembangan lebih lanjut.
Teorema 2.5 Teorema sudut luar (Walter Prenowitz dan Meyer Jordan, 1965:22)
Gambar 2.24 Menunjukkan Bukti:
Misalkan adalah sembarang segitiga, dan misalkan D merupakan perpanjangan dari melalui C. Pertama akan ditunjukkan bahwa lebih besar dari . Misalkan E merupakan titik tengah , dan misalkan merupakan perpanjangan garis yang melalui E hingga F, maka dan (sudut bertolak belakang sama besar). Jadi , dan (bagian segitiga kongruen sama besar). Karena (keseluruhan sudut selalu lebih besar dari bagiannya), sehingga dapat disimpulkan .
Untuk menunjukkan bahwa, perpanjang melalui C hingga H, yang membentuk , dengan menggunakan prosedur bagian pertama pembuktian: misalkan M merupakan titik tengah , perpanjang melalui M, dan lain-lain. Untuk melengkapi bukti, perhatikan bahwa dan merupakan sudut bertolak belakang sehingga sudut tersebut sama besar.
Teorema 2.6 (Walter Prenowitz dan Meyer Jordan,1965: 23)
Jika dua garis dipotong oleh garis transversal sehingga membentuk pasangan sudut dalam bersebrangan yang sama besar, maka garis tersebut sejajar.
Perlu diingat bahwa dua garis dalam bidang yang sama dikatakan sejajar jika garis tidak berpotongan. Misalkan garis transversal membagi dua garis l,m pada titik A, B sehingga membentuk pasangan sudut dalam bersebrangan, dan , yang sama besar, dan misal l dan m tidak sejajar. Maka l dan m akan berpotongan di titik C, membentuk . C terletak pada satu sisi AB atau pada sisi lainnya. Hal ini kontrakdiksi dengan teorema sebelumnya, oleh karena itu l dan m sejajar.
Corollary 2.1. (Walter Prenowitz dan Meyer Jordan, 1965: 24) Dua garis tegak lurus terhadap garis yang sama pasti sejajar.
Akan dibuktikan bahwa jika l tegak lurus m dan l tegak lurus n maka m sejajar n, seperti yang terlihat pada gambar 2.26.
Bukti:
1. l tegak lurus ( keduanya sudut siku-siku ) 2. l tegak lurus
3. ( keduanya sudut siku-siku )
4. Karena dan dua sudut berseberangan maka m dan n (teorema 2.6) (terbukti).
Gambar 2.26 Garis dan dipotong transversal l
Colorray 2.2 (Ekstensi garis sejajar).
Gambar 2.27 Garis Bukti:
Dari titik P hilangkan garis tegak lurus pada garis l yang memiliki kaki di titik Q, dan di titik P bangin garis m yang tegak lurus terhadap PQ. Maka garis m sejajar dengan garis l menurut Corollary 2.1. Terbukti.
Teorema 2.7 (Walter Prenowitz dan Meyer Jordan,1965: 24) Jumlah dua sudut segitiga kurang dari 180.
Gambar 2.28 dengan titik D pada Bukti :
Misalkan merupakan sembarang segitiga. Kita tunjukkan bahwa . Perpanjang melalui titik B hingga titik D. Maka merupakan sudut luar . Dengan menggunakan teorema 2.6 maka . Tetapi , dengan mensubtitusikan pada relasi yang pertama, maka , atau . Jadi, , dengan teorema terbukti.
e. Teorema Saccheri Legendre
Teorema Saccheri Legendre berikut merupakan teorema yang akan digunakan dalam upaya Saccheri membuktikan postulat kesejajaran Euclid. Teorema ini merupakan teorema yang hanyan dapat dibuktikan dalam geometri netral.
Gambar 2.29
Dari teorema 2.8 diatas akibatnya terdapat keistimewaan tentang ukuran jumlah sudut segitiga, sebelumnya telah terbiasa dengan pengertian jumlah ketiga sudut segitiga adalah 180°. Namun demikian, untuk membuktikan tidak dapat dibuktikan dalam geometri netral. Sehingga dalam membuktikan teorema tersebut memerlukan postulat Archimedes tentang dalam pembuktian teorema Saccheri-Legendre. Pembuktiannya adalah sebagai berikut:
Pembuktian dilakukan secara kontradiksi. Asumsikan, jumlah sudut lebih besar dari 180°, misalkan terdapat p, dimana p adalah bilangan positif. Sehingga didapat 180° + p°. Untuk memastikan hal tersebut adalah benar, maka ganti dengan segitiga yang lain dengan ukuran sudut segitiga yang sama, akan tetapi pada salah satu sudutnya setengah dari derajat pada .. Dengan demikian dapat digunakan diulangi untuk segitiga yang lain sehingga jumlah sudutnya adalah 180° + p° akan tetapi pada salah satu sudut dari keempat bilangan tersebut merupakan derajat . Untuk memperoleh jumlah sudut 180° + p° maka, salah satu sudutnya harus berukuran lebih dari p°. Sehingga jumlah ukuran derajat dua sudut lainnya akan lebih besar atau sama dengan 180°, dengan demikian teorema terbukti.■
Ada beberapa pendapat yang menyatakan tentang aksioma yang dituliskan oleh Euclid baik dalam zaman kuno maupun pada zaman modern dengan harapan bahwa aksioma tersebut menjadi lebih jelas dan benar. Pendapat tersebut antara lain:
a. Melalui sebuah titik yang bukan pada garis lurus yang diberikan, hanya satu garis saja yang dapat ditarik dan tak pernah bertemu garis yang diberikan (Playfair)
b. Jumlah sudut sebuah segitiga sama dengan jumlah dua sudut siku-siku. c. Pendapat lain yang mungkin sama untuk memberikan pendapat dan
d. Ada dua segitiga yang tidak sama dan memiliki sudut yang sama(Saccheri dan Plato)
e. Dalam segitiga siku-siku, sisi miring sama dengan jumlah kuadrat sisi-sisi yang lainnya. (Phytagoras).
Pendapat Playfair mendekati Euclid dan dianggap sebagai versi modern yang secara eksplisit menyebutkan garis paralel dan disebut sebagai "dalil paralel". Jumlah sudut segitiga sama dengan dua sudut yang siku-siku. Jauh lebih signifikan adalah aksioma tentang segitiga yang diajukan dalam bentuk yang lebih kuat oleh John Wallis, seorang don Oxford dari abad ketujuh belas dan Geralamo Saccheri, seorang imam Yesuit pada abad kedelapan belas. Menurut Wallis aksioma (3) dapat dibuktikan bahwa jumlah sudut sebuah segitiga sama dengan dua sudut siku-siku.
Argumen lain, dalam gambar 2.2.2 menunjukkan bahwa 'Teorema Pythagoras” mudah dibuktikan dengan cara segitiga serupa. Kita mungkin bertanya dengan bukti Euclid 's "windmill" dari proposisi-nya mengapa Euclid disukai banyak bukti nya lebih rumit. Jawabannya terletak pada asumsi terakhir dalam bukti yang diberikan di gambar 2.2.2, dan akibat adanya kesulitan besaran tidak dapat dibandingkan, sendiri didirikan sebagai konsekuensi dari teorema Pythagoras. Pendapat Meno menunjukkan bahwa diagonal dari persegi memiliki
Gambar 2.2.1 Bukti Segitiga dari Wallis: Misalkan ABC segitiga. Misalkan segitiga AFE = segitiga ABC dan setengah ukurannya. Maka:
AF AE FE 1
AB ACBC2
Jadi, AF = FC dan AE = EB.
Misalkan BD = DC, maka EF = BD = DC
Kemudian segitiga ΔFED� ΔABC, dimana ED =
2 1
AC = AF. Jadi dalam
ΔEFD dan ΔBDE, EF = BD, DF = BE, dan ED berimpitan. Jadi ΔEFD = ΔBDE, dan �DEF = �EDB. Tapi �BCA = �EFA dan �CAB = �CFD, [Dan �ABC = �DFE]. Jadi �ABC + �BCA + �CAB = 180 °.
Telah terbukti bahwa jumlah sudut segitiga adalah jumlah dua sudut siku-siku, dengan demikian hal ini setara dengan paralel postulat Euclid (bukti pendapat b).
Kemudian Euclid dalam teorinya tentang proporsi yang diantisipasi Dedekind tentang definisi dari bilangan real, namun dalam eksposisi geometrisnya disukai secara teknis walaupun lebih rumit tetapi secara konseptual kurang. Pendekatan yang tidak bersangkutan dengan segitiga sama sama sekali.
Gambar 2.2.2 Bukti Pythagoras dengan Segitiga yang sama: Misalkan: ΔABC dengan sudut siku-siku di B. Gambarkan garis tegak lurus dari B keAC di D. Lalu ΔADB�ΔABC dan ΔBDC�ΔABC. Jadi , Dan ,
Jadi (AD + DC).AC = AB2 + BC2. Jadi AC2 = AB2 + BC2.
Diasumsi bahwa sudut Δ berjumlah 180°, dan besar sudut segitiga lainnya sama.
Plato dan Aristoteles melihat bahwa ada universalitas tentang konsep kesamaan, dan kesamaan yang mengharuskan kami memperlakukan sama. Plato berpendapat, diperlukan perlakuan yang sama seperti pada kasus yang sama, tetapi diberi perlakuan berbeda pada kasus berbeda. "Geometris kesetaraan " dicetuskan oleh Plato dan Aristoteles untuk mendasari prinsip bahwa harus ada kesamaan perlakuan untuk semua dengan perbedaan perlakuan aktual pada keadaan yang berbeda. Setiap orang harus diberi bagian yang sama, kata Aristoteles, tetapi mereka adalah bagian yang sama sebanding dengan (Axia) jasa mereka, dan tergantung pada keadaan. Ini berbeda dengan pendapat egalitarian fifthcentury Athena, dan memiliki konsekuensi penting bagi politik berpikir di dunia kuno.
Dari pembuktian tersebut terlihat bahwa teorema Pythagoras setara dengan paralel postulat, sperti yang dikatakan oleh Plato dan Aristoteles.
Bukti:
Dalam sebuah segitiga siku-siku, panjang sisi miring sama dengan jumlah kuadrat di dua sisi lainnya. Dari teorema Pythagoras dibuktikan dengan membagi menjadi tiga jenis utama:
1) Bukti geser, yang tergantung pada teorema bahwa daerah-daerah jajaran genjang (atau segitiga) pada basis yang sama dengan ketinggian yang sama adalah sama,
2) Bukti oleh kesamaan, yang tergantung pada perhitungan proporsi dari sisi segitiga yang sama,
Untuk setiap kasus dari pendapat yang ada, akan lebih mudah ditelusuri jika kembali pada akibat paralel postulat. Dalam pengertian ini, diasumsikan ada aksioma-aksioma geometri bidang (pertama menyiratkan kedua).
Banyak akibat dari Postulat Paralel, diambil bersama-sama dengan aksioma-aksioma yang ada untuk geometri bidang, dapat ditampilkan untuk mengimplikasikan Paralel Postulat. Dalam hal ini, pernyataan ini dapat dianggap sebagai setara dengan Paralel Postulat. Yaitu:
3-3 Dalam setiap segitiga (tiga sudut), jumlah dua sudut siku-siku.
4-4 Dalam setiap segitiga, masing-masing sudut luar sama dengan jumlah sudut luar terpencil.
5-5 Jika dua garis sejajar dipotong oleh suatu transversal, sudut luar alternative adalah sama dan sudut yang sesuai juga sama.
Banyak pernyataan yang ternyata lemah, hal ini ditunjukkan setara dengan Paralel Postulat, yaitu:
6-6 Ada beberapa segitiga yang tiga sudutnya adalah jumlah dua sudut siku-siku. 7-7 Ada sebuah segitiga sama kaki yang tiga sudutnya adalah jumlah dua sudut siku-siku.
8-8 Terdapat segitiga siku sama kaki yang jumlah dua sudut-sudut siku-sikunya sama.
9-9 Tiga sudut dari setiap segitiga siku-siku jumlah dua sudut siku-siku.
Gambar 2.2.3 Bukti Saccheri dari Pythagoras: Misalkan �ABC adalah sudut siku-suku di B, misalkan BA = CB. Perpanjang CB hingga D, sehingga BD = CB.
Kemudian ΔABC = ΔABD; sehingga AD = AC dan �BDA = �BCA, dan ΔABC = ΔDBA, �BAC = �BAD.
Dengan menggunakan rumus Pythagoras:
2 2 2
AC BA CB
2
2CB
2 2 2
AD BA BD
2 2
2BD 2CB
2 2 2
AC AD CD
Jadi �CAD adalah sudut siku-siku, dan �ABC��CAD.
Kenyataan bahwa proposisi Pythagoras bukan diambil sebagai teorema, harus dibuktikan dari aksioma Euclid's, dengan menggunakan aksioma karakteristik geometri yang menunjukkan bahwa kita dapat mengubah nama geometri Euclidean "Pythagoras geometri". Meskipun Euclid, bersama dengan Plato dan Eudoxus, bertanggung jawab secara sistematis sebagai teori aksiomatik, kita perlu memandang proposisi Pythagoras dari beberapa sudut pandang yang paling khas dan mendasar.
lebih baik, Saccheri mengabiskan bertahun-tahun untuk mencoba membuktikan kelima postulat dengan mereduksi dan penyerapan, asumsi itu menjadi salah dan mencoba mendapatkan kontradiksi. Usaha ini gagal, tetapi dalam perjalanannya menemukan non-Euclidean geometri. Teorema geometri non-Euclidean membawa mereka ke Saccheri yang lebih masuk akal, meskipun ia tidak bisa memperoleh sebuah inkonsistensi yang formal, tetapi meskipun aneh, mereka benar-benar cukup konsisten, dan kemudian diakui menjadi teorema non-Euclidean geometri,yang akan disebut sebagai geometri “hiperbola”.
3. Geometries Non Euclides
Geometri hiperbolik non-Euclidean adalah geometri yang ditemukan oleh Bolyai, seorang Hungaria dan oleh Lobachevsky, seorang Rusia di awal abad kesembilan belas. Playfair mendalilkan bahwa dari titik yang bukan pada garis hanya satu baris dapat ditarik sejajar dengan garis, didalilkan dari sudut tidak garis diberikan lebih dari satu, pada kenyataannya, tak terhingga banyak baris dapat ditarik sejajar dengan garis. Kemudian pada abad kesembilan belas mengubah Riemann paralel mendalilkan cara lain, sehingga bisa diambil bahkan garis paralel, ini memerlukan beberapa modifikasi lebih lanjut dari aksioma orang lain, tetapi dengan modifikasi ini diproduksi lain non-Euclidean geometri konsisten, yang “Elliptica” disebut geometri.
sehingga jumlah sudut yang menambahkan hingga tiga sudut kanan 270°, bukan hanya dua sudut siku-siku 180°. Sebuah segitiga kecil akan jumlah sudut yang mendekati 180°, yang cenderung sebagai segitiga semakin kecil dan lebih kecil. Bahkan, jika kita tahu bagaimana sudut, kita dapat mengatakan apa yang seharusnya menjadi hanya sisi bulat segitiga dengan masing-masing sudut nya 90° adalah mereka yang sisi-sisinya adalah satu-seperempat dari keliling lingkaran besar.
Jauh lebih sulit untuk memberikan permukaan dengan lengkungan negatif. Permukaan kursi atau gunung, adalah salah satu contoh. Pada permukaan keliling lingkaran adalah 2 π, dan Sejalan kuadrat dari sisi miring lebih besar dari jumlah dari kuadrat kedua sisi lainnya. Hal ini kurang mudah untuk melihat bahwa jumlah sudut segitiga adalah kurang dari 180°, tetapi jika kita mempertimbangkan bagaimana sangat kecil perbedaan di jalur oneâs dalam melewati gunung dapat menyebabkan tempat yang terpisah, kita menerima bahwa segitiga bisa memiliki sudut yang menambahkan hingga kurang dari 180°. Jika kita mengambil segitiga fitur untuk membatasi, maka ada area minimum segitiga. Ini menunjukkan sekali lagi bagaimana asumsi kegagalan Saccheri Wallis non-Euclidean geometri. Hal ini juga menarik perhatian karakteristik lain dari non-Euclidean geometri. Geometri hiperbolik dan unit berbentuk bulat panjang telah ânatural, dalam geometri hiperbolik ada area minimum yang dapat memiliki segitiga, dan geometri eliptik ada panjang maksimum yang dapat memiliki sebuah baris. (Bahwa kita perlu untuk memodifikasi geometri geometri eliptik Euclid mendalilkan kelima tidak hanya tetapi yang kedua, yang mengasumsikan bahwa sebuah garis lurus dapat diperpanjang tanpa batas jauh.)
Non-Euclidean geometri tetap orang asing. Bisakah kita membawa beberapa pengetahuan dari mereka dan melihat sampai batas tertentu, tetapi memiliki fitur yang tidak terbiasa dan mungkin tetap salah bahkan setelah persahabatan yang panjang, tetapi itu tidak berarti mereka tidak kompatibel. Dan sebenarnya non-Euclidean geometri konsisten.
adalah sebagai absurd tidak kompatibel, dan itu terbukti salah? Pada akhir Felix Klein telah terbukti salah, dengan bukti “relative consistency proof” yang telah menjadi sangat penting dalam dasar matematika. Klein model geometri hiperbolik dalam geometri Euclidean. Dianggap sebagai salah satu bagian yang diberikan oleh redescribing circle dalam bahwa lingkaran Euclidean plane khususnya menunjukkan bahwa di bawah deskripsi baru bertemu aksioma geometri hiperbolik. Lalu ia mengatakan bahwa jika mereka maka semua konsisten, untuk kemudian akan ada inkonsistensi pada bidang Euclidean, dan geometri Euclidean akan terlalu tidak konsisten. Jadi, contrapositively, geometri hiperbolik konsisten selalu geometri Euclid hiperbolik konsisten sehubungan dengan geometri Euclidean.
dari bentuk A' ¬A', yang pada dasarnya membentuk A ¬A terlalu, dan tiga-˄ ˄ dimensi geometri Euclidean akan menjadi tidak konsisten. Sebagai tiga-dimensi geometri Euclidean tidak konsisten, geometri elips tidak konsisten, mengingat bahwa tiga-dimensi geometri Euclidean adalah konsisten, maka itu adalah geometri terlalu elips.
Non-Euclidean geometri begitu diklaim pada skor konsistensi. Dan dalam ketiadaan matematikawan inkoherensi lengkap dan mengucapkan sudah sulit sekali untuk membenarkan mengesampingkan alasan lain.
4. Geometri Formal dan Physical
Geometri Euclidean di turunkan dari kuasanya, geometri tersebut di anggap tidak benar lagi. Ahli filsafat harus mengkaji ulang kembali tentang geometri, seperti teori relativitas oleh Einstein pada awal abad 20. Mereka menyimpulkan bahwa geometri dipengaruhi dua cara: pertama, secara formal dapat disimpulan bahwa ada kasus yang terjadi dalam aksioma, kasusnya adalah pemalsuan cara yang sama dalam teori ilmiah.
Maksud standar modern telah membedakan pendekatan sintaksis formal yang semantik dalam tradisi Protagoras. Kami mempertimbangkan tidak hanya aksioma geometri, Euclid mengatakan aksioma ini sama dengan interpretasi fisik. Interpretasi fisik yang standar dengan sinar cahaya yang dianggap garis lurus. Daripada penerapkan aksioma geometri Euclidean, kita harus mempertimbangkan gabungan dari aksioma dengan interpretasi fisik dan menanyakan apakah mereka benar-benar terbukti. Riemann mempertimbangkan pertanyaan ini dan bukan proposisi Pythagoras, kita dapat menyingkat Pyth, tetapi jika sudut segitiga menambahkan hingga 180° dan peneliti mengukur sudut di puncak tertinggi dan menemukan limit dari ketelitian yang tersebut. Dengan cara ini geometri dapat dianggap sebagai ilmu empiris dan diverifikasi dengan cara yang sama bahwa teori fisik dapat dinyatakan benar.
untuk melakukan penyesuaian interpretasi. Sinar cahaya yang disediakan tidak dapat untuk menentukan garis lurus, kemudian bahkan jika sudut ukuran segitiga menambahkan hingga 180° kebenaran geometri Euclidean tidak diragukan.
Poincare membuat poin penting yang perlu dipertimbangkan dengan serius dari "Konvensi" yang disayangkan. Konvensi yang sebenarnya adalah di mana tidak ada untuk memilih antara dua program tindakan, misalnya Jika Anda berkendara di sebelah kanan atau kiri jalan, atau perkalian dianggap sebagai lebih atau kurang mengikat, media mengabaikan pergi, jumlah itu dan kita perlu memiliki aturan untuk memahami dan konser tindakan kita. Pilihan geometri tidak. Mungkin ada alasan yang baik, mungkin empiris, mungkin tidak, untuk memilih antara geometri satu sama lain. Hempel claims berdebat bahwa kita harus mempertimbangkan tidak hanya kesederhanaan geometri, tetapi juga dari geometri dengan interpretasi fisik. Jika dua interpretasi fisik, PhysInt₁ and PhysInt₂ dan kemudian kadang-kadang Euclid+PhysInt₁ dapat lebih rumit daripada Riemann + PhysInt₂, sehingga kita memiliki alasan rasional untuk lebih memilih yang terakhir, meskipun mantan konsisten dengan fakta yang teramati. Hempel menunjukkan bahwa kita harus memilih yang terbaik, yaitu kombinasi sederhana dari aksioma interpretasi geometris dan fisik bersama-sama. Jika kita berpikir dalam interpretasi fisik, yang berbeda PhysInt₁ PhysInt₂, PhysInt₃, kita akan memiliki interpretasi semantik yang berbeda dari aksioma dan teorema geometri, yang dapat diwakili oleh=
So we might have PhysInt₁= Pyth where Pyth is the Pythagorean proposition,
but PhysInt₂= ¬Pyth and PhysInt₃= ¬Pyth
So PhysInt₂ ¬∆=
and, correspondingly, PhysInt₂ = ¬Pyth
Meskipun kita dapat menempel pada geometri Euclidean harus memiliki, akan masuk akal untuk melakukannya, kombinasi dari geometri elips, teori umum Einstein adalah membeli lebih baik dari geometri Euclidean, bersama dengan beberapa fisika sangat rumit, yang memainkan garis-garis seperti PhysInt₁ bahwa Pyth PhysInt₁, namun dengan mengorbankan banyak hipotesis adhoc dan serangkaian asumsi yang masuk akal.
5. Konsep Pembatasan
Program Geometrodynamics adalah untuk menyatukan fisika dan geometri, untuk mengurangi penjelasan fisika dan geometri. Dalam Teori Umum Einstein digantikan oleh kelengkungan ruang yang rumit. Jika program berhasil, maka tidak ada perbedaan antara geometri dan fisika, dan tidak banyak yang gagal. Begitu banyak dapat diberikan. Tapi program ini bukan fakta. Dan jika berhasil, geometrodynamics dapat sukses, kita tidak harus geometri, namun geometrodynamics. Kemungkinan account monistik dipresentasikan oleh Spinoza, dan penuh semangat yang dilakukan oleh fisikawan kontemporer. Jika pada kenyataannya, kita dapat menghasilkan perubahan dalam struktur konseptual dan perbedaan yang lama antara geometri dan fisika akan ditumbangkan. Tapi selama kita berbicara tentang geometri dan tidak geometrodynamics, ada kontras antara geometri dan fisika, dan keterbatasan konseptual yang kontras ini dapat dikenakan pada jenis geometri yang layak untuk diadopsi.
mencoba untuk menunjukkan link yang lain konseptual. Mari kita survei secara sistematis.
Kami memiliki beberapa perbedaan mereological pertama dan kategoris: 1. (i) titik tidak memiliki bagian (Pythagoras)
(ii) titik memiliki posisi tapi tidak besar, sementara ('i) bagian garis lurus
(ii')(a) garis lurus memiliki posisi dan arah
('ii)(b) garis lurus memiliki panjang tetapi tidak lebar,
Kita memiliki perbedaan kedua topologi antara titik dan garis (tidak selalu lurus):
2. (i)(a) titik tidak dapat memiliki batas, tetapi (b) dapat batas
(ii)(a)garis dapat memiliki titik sebagai batas, dan (b)dapat menjadi batas permukaan
(iii)(a)permukaan dapat memiliki garis sebagai batas dan (b)dapat menjadi batas volume
lebih umum, kita memiliki sejumlah definisi yang mungkin dari garis lurus. Sebuah garis lurus:
3 (i) adalah jarak terpendek antara dua titik (ii) panjang breadthless
(iii) adalah bagian dari sinar cahaya (iv) terlihat lurus
(v) tidak memiliki Kinks
(vi) terletak merata pada dirinya sendiri (vii) adalah sumbu rotasi tiga dimensi (viii) adalah persimpangan dari dua bidang (ix) adalah yang tengah meliputi penutup
Poin tidak hanya entitas yang memenuhi aksioma dari beberapa teori geometris formal, tetapi terkait dengan mereology Aristoteles dan kategori kuantitas, "Berapa?"
Perbedaan yang tersirat dalam cara yang garis dapat dan tidak dapat bagian menjadi lebih eksplisit dalam topologi. Topologi memberikan definisi induktif dimensi dalam hal batas. Set nol memiliki dimensi -1, titik-titik yang tidak memiliki batas, memiliki dimensi 0; garis batas poin yang memiliki dimensi 1; permukaan yang batas-batas garis, memiliki dimensi 2, dan seterusnya. Plato di jalur ini. Dalam Meno mendefinisikan bentuk bidang sebagai batas yang solid: (pir stereou einai skema). Ada banyak proto-topologi Plato dan Aristoteles. Meskipun kami menganggap Kant sebagai pendiri topologi, dan benar, kita harus mengenali lebih daripada yang mereka lakukan upaya pertama dalam hal ini dibuat oleh orang Yunani.
tidak tersedia, atau percaya untuk dapat diandalkan, kita bisa mencoba aturan dengan rantai ketat. Sebuah garis lurus adalah jarak terpendek antara dua titik. Karakterisasi Âgeodesicâ adalah kelurusan dan sangat disukai dalam teori relativitas umum. Konsep-konsep tambahan, seperti âdistanceâ dan titik betweener âbeing, tetapi dapat didefinisikan setidaknya sebagian, tanpa mengasumsikan garis lurus. Sebuah pendekatan yang berbeda lagi adalah untuk memeriksa dua tepi lurus terhadap satu sama lain dengan menjalankan mereka satu sama lain. Jika Anda benar-benar lurus sesuai dengan nyaman bersama-sama sepanjang waktu kalau keduanya kusut bersama-sama, masuk dalam satu posisi, tetapi tidak pada orang lain. Dalam kasus ekstrim kita dapat melihat atau merasakan Kinks dan menolak garis lurus dari tangan. Lurus tidak termasuk Kinks, yang titik-titik singularitas. Dalam hal ini kita mengikuti definisi Euclid dari garis lurus sebagai salah satu bidang datar. Dalam jargon modern, garis lurus memiliki simetri yang sempurna dari terjemahan sepanjang itu. Ini juga memiliki simetri yang sempurna sekitar dirinya. Sebuah sumbu putar adalah garis lurus, dan aku bisa mencoba kebenaran batang tipis perlahan-lahan menyalakan mesin bubut.
yang mungkin hanya ketika x = 0. Mengingat cara untuk menghasilkan optik datar, sangat lurus sehingga kita dapat menghasilkan perpotongan dua optical planes.
Anselmus mendefinisikan Tuhan sebagai id quo maius nequeat cogitari esse, yang tidak bisa membandingkan dengan yang lain: jika kita mendefinisikan sebuah titik yang tidak memiliki bagian atau besarnya adalah nol, dapat dikatakan sebagai id quo minus nequet cogitari esse, tidak ada yang dapat membayangkan dengan yang lebih kecil. Titik bukan hanya susuatu yang benar-benar ada dan dipenuhi dalam beberapa aksioma dari teori geometri tetapi berhubungan dengan mereology dan kategori kuantitas kategori dari Aristoteles.
Jika kita menafsirkan dalam definisi, titik tidak memiliki besaran. Titik memiliki posisi, tetapi letak titik tersebut selalu dapat diketahui.
Perbedaan yang implisit dalam cara menjelaskan suatu garis dapat dan tidak dapat mempunyai beberapa bagian ini dibuat lebih eksplisit dalam topologi. Topologi memberikan definisi induktif dari dimensi dalam hal batasan-batasan. Himpunan nol memiliki dimensi -1; titik-titik, yang tidak memiliki batasan-batasan, memiliki dimensi 0; garis, dimana yang batasan-batasannya merupakan titik, memiliki dimensi 1; bidang, dimana batasan-batasannya yaitu garis, memiliki dimensi 2, dan seterusnya. Plato sudah mengetahui hal ini sebelumnya. Plato mendefinisikan suatu bidang sebagai batasan-batasan yang solid: (stereou peras schema einai). Ada banyak proto-topologi Plato dan Aristoteles. Meskipun kami menganggap Kant sebagai pendiri topologi, dan benar, tetapi kita harus tau bahwa yunani memegang peran penting dalam topologi.
akan mendekekati garis normal. Contoh yang lain dari garis lurus dalam kehidupan sehari-hari yaitu dapat berupa suatu mistar ataupun juga menggunakan benang. Suatu garis lurus merupakan jarak terpendek dari dua titik, yang merupakan bagian dari teori umum relatifitas, sehingga dapat mengetahui konsep lain seperti jarak dan gabungan dari dua titik, tetapi keduanya dapat didefinisikan secara berbeda. Untuk mengetahui dua garis dikatakan garis lurus, maka dapat digunakan dua benang yang ujung-ujungnya ditarik sehingga kedua benang tersebut berhimpitan.
Hal ini bermanfaat bukan hanya untuk penjelasan mengenai bidang optik, karena bidang datar optik membutuhkan sesuatu yang sangat tipis yaitu dengan cara mengasah bidang satu dengan bidang yang lain sampai seterusnya. Diketahui bahwa ketika dua bidang saling bergesekan (diasah), kita tidak dapat memastikan apakah keduanya tipis, karena bisa jadi keduanya menjadi cembung atau cekung. Jika yang kedua diasah terhadap ke tiga, manapun titik tinggi dari yang kedua akan berkorespondensi dengan titik rendah pada yang ke tiga. Tetapi, ketika ini di asah dengan yang pertama, titik rendah akan menjadi kebalikan dari titik rendah tersebut, dan kebalikan titik tinggi, dan demikian yang tinggi akan mengasah satu sama lain. Dalam matematika, dapat dimisalkan jika titik pertama yaitu x berada diatas bidang, maka titik yang kedua berada dibawah bidang yaitu –x, dan titik yang ketiga berada dibawah titik kedua yaitu x. Tiap-tiap operasi pengasahan akan mengubah x menjadi –x yang merupakan hasil perkalian dengan -1. Sehingga dengan tiga bidang maka akan menghasilkan suatu perkalian x dengan (-1)^3 dengan x ≠ 0. Dengan cara pembuatan bidang optik, kita dapat menghasilkan garis yang sangat lurus yang merupakan perpotongan dari dua bidang optik.
6. Which Geometry?
sistem formal. Kita juga tidak bisa, sebagai empiris, yang berarti meninggalkan itu seluruhnya untuk memutuskan perbedaan antara sistem formal dengan empiris. Kita tidak bisa mempertahankan suatu pembuktian tanpa menggunakan perhitungan empiris. Oleh karena itu, kita harus bertanya pada diri kita sendiri, bagaimana kita harus memilih suatu geometri, yang menjamin bahwa terdapat banyak kesamaan(konsisten) dari yang sudah dipilih.
Mari kita tabulasikan mereka sesuai dengan karakteristik khususnya untuk membuat pilihan informasi diantara mereka seperti dalam majalah konsumen.
Hyperbolik Euclidean Elliptik
Area minimum No natural unit Panjang maksimum Area maksimum Table 2.6.1
Tidak satupun dari geometri tersebut yang meyakinkan kesemuanya: tidak satupun dari mereka yang tidak konsisten. Kita tidak mengatakan bahwa kesemuanya tidak direkomendasikan, dan harus membolehkan salah satu dari mereka mungkin yang paling sesuai untuk beberapa tujuan tertentu. Kita dapat memberikan suatu pemecahan yaitu dengan menggunakan geometri Euclid. Alasannya yaitu:
Fleksibilitas dari geometri Euclid ditampilkan lebih jelas dalam formulasi Saccheri-Wallis, dimana terdapat pengaruh pada geometri Euclid yang memberikan kemungkinan untuk memiliki dua figures (gambar) berbentuk sama tetapi ukuran yang berbeda. Dalam geometri eliptik, seperti yang kita lihat dengan alat bola, bentuk menentukan ukuran, dan sama halnya dengan geometri hiperbolik. Tidak ada kemungkinan dalam geometri dari model skala, yang mampu mencirikan objek dan figures lainnya dengan mengacu pada bentuk dan ukuran bebas, kita seharusnya hanya memiliki satu cara untuk mengkarakterisasi mereka. Geometri euclid memiliki derajat bebas, dan karena itu lebih cocok untuk fungsi sebagai back clothe-deskriptif terhadap fenomena fisik yang dapat dijelaskan dan dirumuskan dan diuji teori fisika. Sedangkan untuk sebuah teori ilmiah seperti fisika, fleksibilitas mungkin suatu kesalahan, dan mencegah teori tersebut dipalsukan. Pada geometri, fleksibilitas bukanlah suatu kelemahan, tetapi suatu kekuatan.
Pertimbangan yang sama berlaku untuk jumlah paralel. Geometri Euclid memiliki tepat satu, dan lebih spesifik dari pada geometri hiperbolik yang memiliki tak terhingga banyaknya, meskipun dalam kasus ini tidak lebih spesifik daripada eliptik dimana tidak mempunyai sama sekali. Tetapi yang kedua terdapat kesalahan dalam menetapkan system acuan. Pada permukaan dunia, garis bujur berpotongan di kutub 10oE dan 90oN yang sama dengan 10oW dan 90oN. Ini adalah suatu kesalahan di dalam suatu sistem acuan. Kita ingin terdapat suatu korespondensi satu-satu antar titik pada ruang dan bidang dari koordinat.