Statistical treatment of umbra length inside willow coppice
J. Ross
∗, M. Mõttus
Tartu Observatory, Tõravere, 61602 Tartumaa, Estonia
Received 31 March 1999; received in revised form 7 October 1999; accepted 13 October 1999
Abstract
Measurements of the statistical characteristics of umbra and sunflecks at different depths inside a willow coppice — Salix viminalis and Salix dasyclados — were carried out at Tartu Observatory, Tõravere, Estonia, in 1997. A new instrument, the sunfleck indicator, constructed by M. Sulev, was used. This instrument, moving perpendicularly to rows in the horizontal direction, counts the number and length of sunflecks and umbrae at a level where downward cumulative leaf area index is L. During statistical data processing, several umbra characteristics — umbra length distribution function, mean number of umbrae, mean umbra length, fractional area of umbra, etc. — were calculated at different measurement heights as the functions of the optical path lengthτ=L/sin h, where h is the solar elevation.
The number of umbrae NU increases rapidly at smallτ, has a maximum at τ≈3–4 and decreases slowly with further
increase inτ. This interrelationship was fitted by an exponential function. Umbra length distribution function can be divided into three regions: small umbrae (0–10 cm in length), medium-length umbrae (10–20 cm) and long umbrae (up to 100 cm). At all depths the number of small umbrae exceeds the number of medium-length and long umbrae by 3–10 times. The fractional area of umbra kU(τ) increases withτand was approximated by a rectangular hyperbola. In lower layers (τ=8–12) kU(τ)
reaches 0.85–0.90 and these layers are dominated by umbra. ©2000 Elsevier Science B.V. All rights reserved.
Keywords: Willow coppice; PAR variability; Statistical umbra characteristics
1. Introduction
Inside a plant canopy, PAR is characterized by great spatial and temporal variability (Ross, 1981; Chazdon, 1988); in some middle canopy layer, PAR global irra-diance may vary about 50-fold with a rapid sequence of sunflecks, penumbra and umbra.
Statistical treatment of umbra and sunflecks is closely related to the progress of new comprehen-sive computer models of canopy photosynthesis and evapotranspiration, which require detailed 3D
char-∗Corresponding author. Tel.:+372-7-410-265;
fax:+372-7-410-205.
E-mail address: [email protected] (J. Ross).
acteristics of different radiation types for input. Since the interrelationship between PAR and photosynthesis is nonlinear, mean values of radiation do not yield correct results. In our opinion, for further calculation of canopy photosynthesis leaves in plant canopies should be divided into three groups according to the type of direct sunlight they receive: sunflecks, umbra and penumbra; and photosynthesis should be calculated separately for each group. Therefore, it is necessary to know the area of umbra, its vertical distribution and temporal dynamics so that different data for umbra, penumbra and sunflecks can be used in modern radiation transfer models.
The second possible application area of umbra statistics is the study of understorey growth and
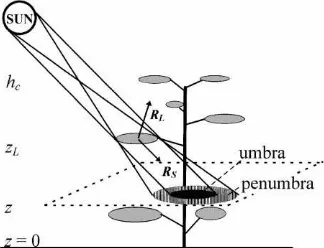
Fig. 1. The shadowing effect of a single leaf. hc— coppice height, zL — leaf height, z — measurement height, RS — direction of sunrays, RL — direction of leaf normal.
renewal of vegetation. In understorey growth, umbra length distribution, and temporal dynamics play a certain role.
According to Oker-Blom (1984), Myneni and Im-pens (1985) and Ross et al. (1998) sunfleck, penumbra and umbra can be defined as follows (Fig. 1):
1. sunfleck is an area inside plant canopy where the sun’s disc is not shaded by any phytoelements. In sunflecks, direct solar irradiation S(h), which de-pends on solar elevation h, is a nonrandom quan-tity, i.e. S(h)=S0(h), where S0(h) is direct solar
irradiation above the canopy;
2. penumbra is an area inside plant canopy where the sun’s disc is partly covered by phytoele-ments. In penumbra, S(h) is a random quantity and 0<S(h)<S0(h);
3. umbra is an area inside plant canopy where the sun’s disc is fully covered by phytoelements and S(h)=0.
1.1. Literature overview
In 1971, Miller and Norman developed a mathe-matical model for penetration of sunlight into plant canopy (Miller and Norman, 1971a, b). In the first part of the paper, sunfleck size distribution was cal-culated proceeding from the probability that a probe line with the length l would fall completely into sun-light if the sun was a point source at infinity and if the canopy consisted of identical leaves at a fixed distance from flat ground. In the second part, finite dimen-sions of the solar disc were taken into account and
radiation intensity distribution was estimated in penumbra. These two results were combined in Norman et al. (1971), where theoretical results were found to be in good agreement with actual measure-ments in sumac and sunflower canopies.
Several formulae for canopy gap fraction were re-viewed by Nilson (1971): the most common Poisson law, and positive and negative binomial distributions. Nilson also proposed a new formula for gap frequency, based on Markov chains. In Markov models, differ-ent canopy layers are not considered independdiffer-ent, and with proper selection of parameters the model can fit well with experimental data.
Another way to calculate the distribution of solar radiation intensity is computer simulation (Stenberg, 1995; Oker-Blom, 1984, 1985). Monte Carlo meth-ods can yield an estimate of radiation distribution in penumbra for more complicated canopy structures and have shown that penumbra makes a considerable con-tribution to total photosynthesis, especially in lower canopy layers.
Chen and Black (1992) and Chen and Cihlar (1995a, b) have developed a method for estimating leaf area index from direct solar radiation measurements. They attempt to account for foliage clumping and nonran-dom gaps in the canopy using the gap size distribu-tion proposed by Miller and Norman (1971a) and the formula for fractional sunfleck area proposed by Nil-son (1971). Due to foliage clumps, effective leaf area intercepting solar radiation is reduced by about 30%, while a single leaf may not be the basic foliage ele-ment responsible for radiation interception, especially in conifers. A method for calculation of the character-istic width of a basic foliage element is developed in Chen and Black (1992).
Ross et al. (1998) proposed a statistical treatment of PAR variability and its application to willow coppice. In this treatment, statistical distribution of PAR global irradiance, obtained with a LI-COR quantum sensor, was approximated by normal distribution in sunfleck and umbra areas, and the fractional area of penumbra was studied as a function of canopy depth and solar elevation h. Umbra and sunfleck length were not ex-amined.
Fig. 2. Sunfleck indicator.
The objective of this paper is to study different statistical parameters of umbra length distribution, umbra fractional area, number of umbrae, mean um-bra length, etc. in different canopy layers as the func-tions of the optical depth τ=L/sin h for both Salix viminalis and Salix dasyclados coppices. For this pur-pose, a new instrument, the sunfleck indicator (Fig. 2), constructed by M. Sulev, was used. Moving in the horizontal direction at different canopy depths, this instrument measures the length of sunflecks and umbrae.
2. Materials and methods
Radiation and phytometrical measurements were carried out during the vegetation period of 1997 in a 4-year-old willow coppice of S. viminalis, clone 78021, and S. dasyclados, clone 81090, located at Tartu Observatory, Tõravere (latitude 58◦16′N, longitude 26◦28′E, altitude 70 m above sea level), Estonia.
The plantation was established in May 1993 on the flat top of a hillock on light pseudopodzolic soil (Planosol). Cuttings were planted in double row, the distance between plants in a row being 0.5 m. The
azimuth angle of rows was 75◦, planting density was 20,000 cuttings per ha.
A special measurement system was designed for ex-perimental study of the variability of radiation charac-teristics within the willow coppice (Ross et al., 1998). The measurement system (Fig. 3) consisted of a 6-m long horizontal bar placed perpendicularly to the rows inside the willow plantation with a sensor carriage moving along it at 30 mm s−1. Two Reemann pyra-nometers (TR-3) for measuring downward and up-ward fluxes of global radiation, two LI-COR quan-tum sensors (LI-190SA) for measuring downward and upward fluxes of PAR, a miniature Reemann net ra-diometer (MB-1) for measuring net radiation, and a sunfleck indicator for detecting sunfleck and umbra were mounted on the carriage.
The sunfleck indicator (Fig. 2) is, in principle, a miniature actinometer with an angle of view of 10◦in the vertical direction and 15◦ in the horizontal direc-tion. Such an angle of view guarantees that the sun will remain completely in the field of view for 6 min. A silicone photodiode was used as a sensor, and the instrument was calibrated on the pyrheliometric scale using a reference actinometer. Due to different spec-tral sensitivities of receivers and a special configura-tion of the field of view, this calibraconfigura-tion provides only approximate values in energy units.
The sunfleck indicator has polar mounting and must be directed manually to the sun before each scan. The accuracy of determination of the linear dimensions of sunflecks and umbrae is±5 mm.
The height of the horizontal bar inside coppice can be changed from 0.4 to 6 m, the measurement heights used on selected days are given in Table 1.
One measurement scan consisted of a transit of the carriage from one end of the bar to the other and back with a total scan length of about 12 m. Due to leaf flutter caused by wind the data obtained from the two
Table 1
Radiation measurement heights and the corresponding values of leaf area index L(z) in a willow coppice on selected days 30 June 1997; Salix dasyclados
Height z (cm) 45 200 280 350 450
L(z) 5.25 5.20 4.30 2.05 0
21 July 1997; Salix viminalis
Fig. 3. Radiation measurement system within willow coppice. M — drive, C — carriage, 1 — sunfleck indicator, 2 — pyranometers, 3 — quantum sensors, 4 — net radiometers.
transits were not identical; to increase the statistical reliability of the sample the two transits were merged into one measurement. The passage took about 400 s, and during each scan 2400 readings were recorded for every sensor.
Radiation measurements were carried out at differ-ent solar elevations with a clear sky. Simultaneously with radiation measurements, air temperature and hu-midity inside and outside coppice, surface tempera-ture beneath coppice, broadband direct solar radia-tion, photosynthetically active direct solar radiation S0, broadband global radiation, global PAR, and wind
speed above the canopy were recorded.
The data acquisition system consisted of a multi-channel data logger (Delta-T Devices) and a PC. Voltage readings from the sunfleck indicator were converted to the metric system (W m−2) using the
approximate calibration coefficient.
In Fig. 4, two recordings of the sunfleck indicator are presented. In the coppice with height hc=475 cm,
at the height of z=350 cm, z/hc=0.74 (a), sunflecks,
penumbra and umbra are all present, with umbra occu-pying 42% of scan length. The situation is totally dif-ferent at the height of z=45 cm, z/hc=0.09 (b).
Sun-flecks have disappeared and the part of penumbra is relatively small as umbra occupies 80% of scan length.
In the statistical processing of the sunfleck indica-tor’s recordings, two methodological problems must be solved: (i) how to determine the irradiance SFS
separating sunflecks from penumbra (sunfleck thresh-old), and (ii) how to determine the irradiance SFU
sep-arating umbra from penumbra (umbra threshold). For two uppermost measurement levels, sunfleck fractional areas KSwere calculated using different
val-ues of SFS/SF, where SF is the sunfleck indicator’s
reading above canopy.
Analogously, for two lower measurement levels the sunfleck indicator’s recordings were cut at different values of SFU/SF, and the corresponding umbra
frac-tional areas were calculated.
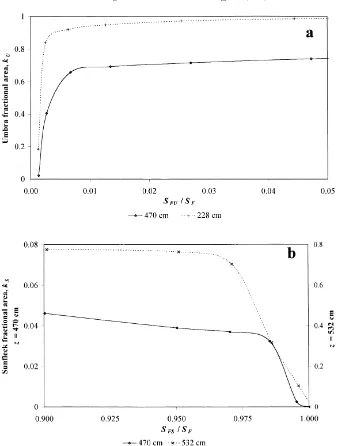
Fig. 5a shows that umbra fractional area increases rapidly with umbra threshold until SFU/SF≈0.005
and then remains almost constant. Sunfleck fractional area (Fig. 5b) depends strongly on SFS/SF at SFS/SF
values larger than 0.98. This is probably due to fluc-tuations of direct solar irradiation above the canopy SF as well as due to measurement uncertainties.
At lower values of SFS/SF the slope of kS is much
smaller.
To eliminate noise and fluctuations of SF in further
Fig. 4. Sunfleck indicator readings in a S. dasyclados coppice on two scans on 30 June 1997.
(a) (b)
height z, cm 350 45
coppice height hc, cm 475 475
z/hc 0.74 0.09
leaf area index L 2.05 5.25
solar elevation h, 35.6 51.0
optical path lengthτ 3.52 6.76
Fig. 5. Umbra and sunfleck discrimination level in S. viminalis: (a) umbra fractional area kU as a function of umbra threshold SFU/SF at two measurement heights, 470 and 228 cm; (b) sunfleck fractional area kS as a function of sunfleck threshold at 470 (left-hand axis) and 532 cm (right-hand axis) as a function of sunfleck threshold SFS/SF. The measuring heights 228, 470 and 532 cm constitute 0.37, 0.77 and 0.87 of the coppice height hc=610 cm, respectively.
2.1. Phytometrical characteristics of willow coppice
The architecture of a willow coppice during the first three growing years is characterized more in detail in Ross and Ross (1998).
The coppice can be divided into three layers: 1. The uppermost layer is made up of almost vertical
Table 2
Coppice height hc, leaf area index L, and layer thicknesses on selected days
2. The middle foliage layer can be modelled as a horizontally homogeneous turbid plate medium where individual branches are indistinguishable. 3. The lowest foliage layer is almost leafless and
contains mostly cylindrical, nearly vertical stems. Some phytometrical characteristics of S. viminalis and S. dasyclados coppices, measured on selected days, are given in Table 2.
The vertical distribution of leaf area density uL(z)
for both subspecies shows that in the upper layer with a thickness of about 200 cm, leaf area density increases almost linearly, accounting for 60–80% of total leaf area.
Compared with S. dasyclados, S. viminalis leaves are longer and narrower. The mean area of a S. vim-inalis leaf is about 4.0 cm2, that of a S. dasyclados leaf, about 4.9 cm2. The variability of leaf dimensions is large for both subspecies and can be approximated by lognormal distribution (Ross and Ross, 1998).
The stems of a S. viminalis shoot can be modelled as nearly vertical cylinders, unlike the stems of S. dasy-clados which are less vertical and more convex.
3. Statistical treatment
Let us assume some horizontal area A at the depth L. This area can be divided into three parts: AS —
sunfleck area, AP — penumbra area, and AU —
um-bra area, their fractional areas being kS(L,h)=AS/A, kP(L,h)=AP/A, and kU(L,h)=AU/A, respectively.
The measured area of an umbra caused by the shadow of a single leaf (Fig. 1) depends on the following factors:
1. angular diameter of the solar disc (32′);
2. leaf shape and area characterized by its effective diameter;
3. leaf orientation characterized by the normal of leaf surface RL=(θL,ϕL), where θL and ϕL
are the inclination angle and the azimuth angle, respectively;
4. direction of sunrays RS=(θS,ϕS), where θS and ϕSare the solar inclination and azimuth angles,
re-spectively. The leaf area SL, projected onto a
sur-face perpendicular to sun’s rays, is determined by the cosine of the angle between the two directions:
cos∠(RS, RL)=cosθScosθL+sinθSsin θL ×cos(ϕSndash ϕL);
5. distance between the leaf and the sensor, zL−z,
which determines the effective angular diameter of the leaf area projection S′L.
In deeper layers, total shading may be caused by phytoelements located at different distances from the sensor. This cooperative shadowing effect depends on canopy architecture, 3D distribution of branches and stems, size and distribution of individual leaves on shoot cylinders, etc.
These factors cause an extremely great variability of umbra area and make it impossible to calculate it analytically. Therefore a statistical treatment of umbra in a plant canopy is needed.
Let NU(L,h) be the number of umbrae per 1 m of
scan at the depth L and solar elevation h; these um-brae have different lengths varying from 0 tolUmax, and their lengths are statistically distributed over the interval [0,lUmax]. Let nU(l) be umbra length distribu-tion funcdistribu-tion, i.e. the number of umbrae with a length between l and l+1l per 1 m of scan, and
lXUmax
l=0
nU(l)=NU. (1)
In our case, the distance between two consecutive mea-surements,1l=0.7 cm. Mean umbra length is
hlUi =
PlUmax l=0 l nU(l)
NU
(2)
and the fractional area of umbra inside coppice equals umbra length per 1 m of scan:
kU=
lXUmax
l=0
l nU(l). (3)
For analysis of umbra length variability, the umbra length distribution function nU(l) and the cumulative
umbra fractional area function FUare used. FU(l)
de-notes the fraction of a transect occupied by umbrae larger than l, or the fractional area of umbrae with a length from l tolUmax:
FU(l)=
lXUmax
l=0 lnU(l)
or in the integral form
FU(l)=
From (3) and (4) it follows that
FU(0)=kU, FU(lUmax)=0. (5) Analysis of FU(l) and nUshows that it is reasonable
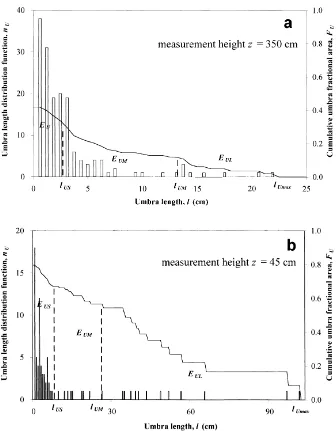
to divide the interval between 0 andlUmax into three parts: (Fig. 6a,b)
Fractional umbra area for each of the intervals kUS, kUM, kULis defined so that
kU=kUS+kUM+kUL. (6)
It should be noted that the location of points lSand lM separating the intervals and, consequently,
frac-tional areas kUS, kUM, and kUL are somewhat
arbi-trary and subjective. In umbra length intervals EUS
and EUM, FU(l) is approximated by a straight line
us-ing the value of FU(l) at the endpoints of the section.
The slope of the line in the short umbra intervalαUS
and in the medium-length umbra intervalαUM can be
calculated from the formulae
The slope of FU(l) is associated with the number of
umbrae in that particular interval, differentiaton of (4) yields Typically, the umbra length distribution function nU(l)
decreases with l, while the decrease is maximum in the small umbra interval EUSand, according to definition,
the cumulative umbra fractional area function FU(l)
decreases continuously. Therefore bothαUSandαUM
are negative andαUS< αUM.
It is appropriate to assume that short umbrae are caused by individual leaves (or a few leaves with um-brae being separated by rays passing through shoots). Hence their lengths are determined by the effective di-ameter of a leaf, while the lengths of medium-length umbrae are determined by the dimensions of shoot cylinders. Large umbrae occur only in deeper canopy layers as a result of cooperative shadowing by shoots and individual leaves.
Analysis of experimental data shows that umbra length characteristics are largely determined by three factors: solar elevation h, depth of the measurement level characterized by L(z), and leaf, plant and canopy architectural characteristics. The first two factors de-termine the optical path length of direct solar radiation in plant canopyτ=L/sin h, expressed in the units of L. Hereafter umbra length characteristics will be con-sidered as the functions of the optical path lengthτ, assuming that it is the key factor which determines the absorption pattern of direct sunlight.
4. Results and discussion
The umbra length distribution function nU(l) (Fig. 6)
is not continuous, especially in the long umbra interval EUL, which indicates that the 12-m scan length is not
adequate for obtaining a complete picture of umbra statistics.
Small umbrae dominate in all layers and the maxi-mum of nU(l) corresponds to l≈0. In the short umbra
interval, FU(l) decreases rapidly with increasing l and
is approximated by a straight line.
It is somewhat unexpected thatαUS has a distinct
up-Fig. 6. Umbra length distribution function nU(l) (left-hand axis) and cumulative umbra fractional area function FU(l) (right-hand axis) calculated from the data in Fig. 4a and b. See Fig. 4 caption for information on scan characteristics. The length interval for nU(l) is 0.7 cm. EUS— short umbra interval, EUM— medium-length umbra interval, EUL— long umbra interval, lUS— maximum length of short umbra, lUM — maximum length of medium-length umbra,lUmax — maximum umbra length.
per coppice layers, causing the occurrence of a large number of small umbrae. Further down, overlapping shadows from different shoots lead to reduction in the number of small umbrae. In deeper layers, large um-brae dominate and nU decreases more slowly withτ,
slowing down decrease in FU(l).
For medium-length umbrae, FU(l) is also
approxi-mated by a straight line.
Ross et al. (1998) have shown that in a S. vimi-nalis coppice, relative mean PAR irradiance above the canopy QrU(τ ) = (QU(τ ))/Q0,where Q0 is global
PAR irradiance in umbra at the depth t, can be approx-imated by the formulaQrU(τ ) = 0.16 exp(−0.34τ ), R2=0.71. At τ=0, QrU(τ ) = 0.16, which corre-sponds to the average fraction of diffuse sky PAR in global PAR.
Fast increase in umbra fractional area with increas-ingτ in middle and deeper layers is caused by coop-erative shadowing, as a result of which large areas are created where the sun is completely shaded by phy-toelements.
The number of umbrae increases rapidly at small τ and has a maximum atτ≈3 for S. viminalis and at τ=4–5 for S. dasyclados (Fig. 7). The data are fitted by the regression function
NU=a(τ3+b)exp(c√τ ),
where a, b, c are regression constants, given in Table 3 together with the square of the correlation coefficient R2and standard error St.
It is obvious that whenτ=0, no phytoelements can occur between the sun and the sensor, and the number of umbrae as well as umbra fractional area must be zero. However, as in the upper canopy layer the leaf area density uL(z) is very small and leaf dimensions
are finite, the number of leaves that can shade the sun is small, and statistical methods prove unreliable. So
Fig. 7. Number of umbrae per 1 m scan length, NU, inside a willow coppice as a function of optical path lengthτ and fitted regression curvesNU=a(τ3+b)exp(c√τ )(see Table 3 for the values of constants).⋄, solid line — S. viminalis;×, dashed line — S. dasyclados. the regression functions used in this study were chosen keeping in mind the asymptotic case whereτ→0, but are applicable only whenτ> 0.5 for S. viminalis and τ> 3 for S. dasyclados.
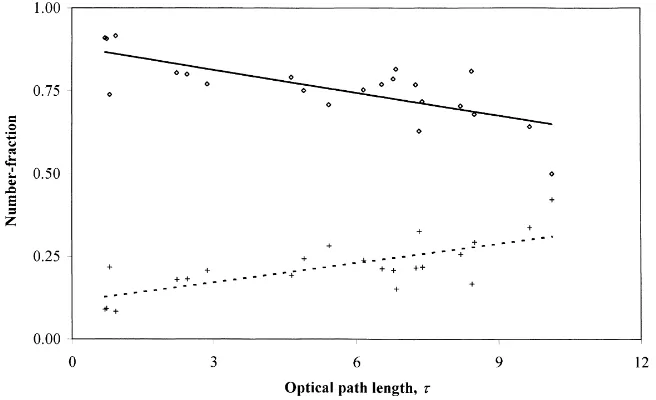
Smaller and narrower leaves of S. viminalis gen-erate more small umbrae compared with larger and wider leaves of S. dasyclados (Fig. 8). The differ-ence becomes less significant in deeper canopy lay-ers where the overlapping shadows of separate shoots generate large umbra areas. For both subspecies, the number-fraction of short umbrae (i.e. the fraction of short umbrae in the total number of umbrae) is larger than 80% in all coppice layers, and short umbrae dom-inate in upper layers where long umbrae do not exist. The number-fraction of short umbrae decreases lin-early for both subspecies, R2=0.53 and R2=0.43 for S. viminalis and S. dasyclados, respectively (Fig. 8).
For S. dasyclados, the number-fraction of
medium-length umbrae depends weakly on τ; the square
of the correlation coefficient of the linear regres-sion shown in Fig. 8b, R2=0.15. For S. vimi-nalis, the number-fraction of medilength um-brae increases noticeably with τ, R2=0.53 (Fig. 8a). As distribution density for medilength um-brae does not depend on τ, the increase must be caused by increase in lUM, which depends on canopy
Table 3
Results of fitting NU by regression function (see text)
a b c R2 S
t
Salix viminalis 218.9 0.014 −3.38 0.812 2.10 Salix dasyclados 56.0 −5.57 −2.88 0.460 1.86
The maximum length of umbrae in the uppermost layers (τ=0.5) is about 5 cm and increases linearly up to 140 cm at ground level.
Larger leaves of S. dasyclados enhance the frac-tion of large umbrae more rapidly with τ compared with narrow leaves of S. viminalis. However, as this increase is concurrent with the constancy of the number-fraction of medium-length umbrae, it may indicate more pronounced clumping at shoot level.
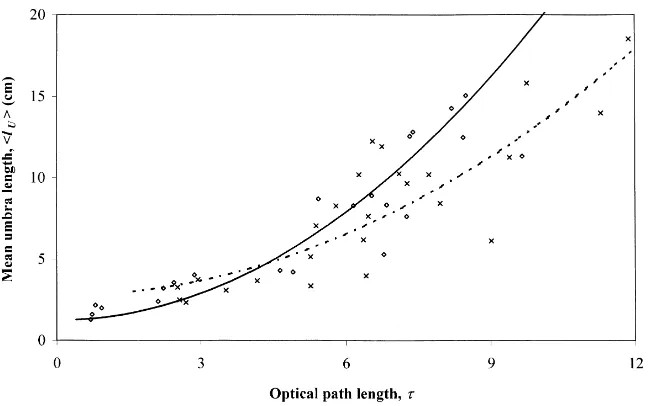
For mean umbra length, there is no major differ-ence between S. viminalis and S. dasyclados (Fig. 9). Data are fitted by the functionhlUi = a + bτ2, the
results of the fitting are given in Table 4. To describe the variability of umbra length, we use the maximum lengths of short (lUS) and medium-length (lUM) umbra
intervals.
The maximum lengths of short and medium-length umbra intervals as the functions of optical path length τ can be fitted by linear regression. There is no ma-jor difference between S. dasyclados and S. viminalis in the short umbra region, lS increases with τ from
Fig. 8. Number-fraction of short (NUS/NU,⋄, solid line) and medium-length (NUM/NU,+, dashed line) umbrae as the functions of optical path lengthτ, linear regression, S. viminalis.
Table 4
Results of fittinghlUiby regression function (see text)
a b R2 S
t
Salix viminalis 1.25 0.18 0.777 3.15 Salix dasyclados 2.72 0.11 0.763 2.20
2–5 cm in the upper layer to about 10 cm near the ground.
The maximum length of medium-length umbrae at the bottom of a S. viminalis coppice is about 30 cm larger than at the bottom of a S. dasyclados coppice. The situation is similar for long umbrae: at ground level maximum umbra length is about 50 cm larger for S. viminalis.
Division of umbrae into three length intervals is somewhat unreliable in upper coppice layers where mutual shadowing by shoot cylinders is not present.
The umbra fractional area kU, i.e. the total length of
Fig. 9. Mean umbra lengthhlUiand fitted regression curveshlUi =a+bτ2 (see Table 4 for the values of constants) vs optical path length
τ.⋄, solid line — S. viminalis;×, dashed line — S. dasyclados.
Experimental data have been fitted by the function
kU(τ )= τ2 a+τ2,
where the value of the constant a=5.90, R2=0.97 for S. viminalis and a=20.5, R2=0.86 for S. dasyclados. Despite the large number of small umbrae, the tran-sect fraction they occupy does not exceed 50–60%
Fig. 10. Umbra fractional area kU inside a willow coppice as a function of the optical path length τ and fitted regression curves
kU(τ )=τ2/(a+τ2).⋄, solid line — S. viminalis;×, dashed line — S. dasyclados.
(Fig. 11) and decreases with τ to 10%. Correlation between kUS/kUandτ is weak.
The share of medium-length umbrae is 15–25% of the total number of umbrae, but their fractional area varies greatly, from a few per cent to 70%.
Fig. 11. Ratio of short umbra fractional area (kUS) to total umbra fractional area (kU), kUS/kU vs optical path lengthτ fitted by a linear regression. (a) S. viminalis; (b) S. dasyclados.
a more expressed cylindrical shoot structure in upper canopy layers. Also, leaf area density function has a wider maximum for this subspecies compared with S. dasyclados, which indicates taller shoots.
Another indicator of different canopy architecture is the ratio of the area of long umbrae to total umbra area. Despite the fact that the average length of umbra is smaller in S. dasyclados, the species produces more long umbra in deeper canopy layers (50–60% of total umbra area) compared with S. viminalis (less than 50% of total umbra area).
5. Concluding remarks
Because of the extreme complexity of natural canopies, analytical models fail to give the distribu-tion of solar radiadistribu-tion in plant canopies with sufficient accuracy.
τ=5–6, about 60% of total umbra in S. dasyclados is contributed by long umbrae, about 10% by short umbrae and only 30% by medium-length umbrae. On the ground under a S. dasyclados coppice, large um-bra areas appear to be separated by intervals of short umbrae, where radiation density changes rapidly.
In a S. viminalis coppice, the amount of umbra con-tributed by medium-length shadows is larger, since individual shoots allow sunrays to penetrate among them. However, the fractional area of short umbrae and the absolute value of the slope of FU(l) in this
in-terval decreases rapidly withτ, and in deeper canopy layers the total number of umbrae for S. viminalis is smaller than for S. dasyclados.
It is surprising that at the same optical path length the wider leaves of S. dasyclados, located closer to the ground, allow more penumbra to fall onto the transect than do the narrow leaves of S. viminalis. This is a certain evidence of a major difference in the stand architecture of the two species.
Differences in the number of umbrae and in the fraction of medilength umbrae suggest that um-bra distribution can be used for estimation of the geo-metrical characteristics of a plant stand. However, as the two subspecies with relatively similar characteris-tics demonstrate quite a different behaviour, correla-tion between umbra fraccorrela-tion and plant architecture is not simple.
It is clear that the statistical characteristics of um-bra and sunflecks are not independent: when the frac-tion of umbra increases, the fracfrac-tion of sunflecks de-creases, and vice versa. This interrelationship is not simple due to the existence of penumbra. For a more detailed study of canopy radiation transfer, umbra and sunflecks should be treated simultaneously.
Whether the methodology used in this paper is ap-propriate for describing the interception of direct so-lar radiation in dense canopies, needs to be cso-larified in future models where empirical coefficients will be correlated with the characteristics of real canopies.
Acknowledgements
This research was supported by ETF grants Nos. 251 and 2668. The authors thank Madis Sulev, Peeter Saarelaid and Enn-Märt Maasik for assistance in field
measurements and Mrs. Ester Jaigma and Mrs. Viivi Randmets for preparing the manuscript. For valuable comments and critical remarks, the authors express their deep gratitude to the anonymous reviewers and to Dr. J. B. Stewart.
References
Chazdon, R.L., 1988. Sunflecks and their importance to forest understorey plants. Adv. Ecol. Res. 18, 1–63.
Chen, J.M., Black, T.A., 1992. Foliage area and architecture of plant canopies from sunfleck size distributions. Agric. For. Meteorol. 60, 249–266.
Chen, J.M., Cihlar, J., 1995a. Plant canopy gap-size analysis theory for improving optical measurements of leaf-area index. Appl. Optics 34, 6211–6222.
Chen, J.M., Cihlar, J., 1995b. Quantifying the effect of canopy architecture on optical measurements of leaf area index using two gap size analysis methods. IEEE Trans. Geosci. Remote Sensing 33, 777–787.
Miller, E.E., Norman, J.M., 1971a. A sunfleck theory for plant canopies I. Lengths of sunlit segments along a transect. Agron. J. 63, 735–738.
Miller, E.E., Norman, J.M., 1971b. A sunfleck theory for plant canopies II. Penumbra effect: intensity distributions along sunfleck segments. Agron. J. 63, 739–743.
Myneni, R.B., Impens, I., 1985. A procedural approach for studying the radiation regime of infinite and truncated foliage spaces Part II. Results and discussion. Agric. For. Meteorol. 34, 3–16.
Nilson, T., 1971. A theoretical analysis of the frequency of gaps in plant stands. Agric. Meteorol. 8, 25–38.
Norman, J.M., Miller, E.E., Tanner, C.B., 1971. Light intensity and sunfleck size distributions in plant canopies. Agron. J. 63, 743–748.
Oker-Blom, P., 1984. Penumbral effects of within-plant and between-plant shading on radiation distribution and leaf photosynthesis: a Monte Carlo simulation. Photosynthetica 18, 522–528.
Oker-Blom, P., 1985. The influence of penumbra on the distribution of direct solar radiation in a canopy of Scots pine. Photosynthetica 19, 312–317.
Ross, J., 1981. The Radiation Regime and Architecture of Plant Stands. Dr. W. Junk Publishers, The Hague, Boston, London, 391 pp.
Ross, J., Sulev, M., Saarelaid, P., 1998. Statistical treatment of the PAR variability and its application to willow coppice. Agric. For. Meteorol. 91, 1–21.
Ross, J., Ross, V., 1998. Statistical description of the architecture of a fast growing willow coppice. Agric. For. Meteorol. 91, 23–37.